Parsing Giuseppe Attardi Universit di Pisa Parsing To

Parsing Giuseppe Attardi Università di Pisa

Parsing To extract the grammatical structure of a sentence, where: sentence = program words = tokens For further information: Aho, Sethi, Ullman, “Compilers: Principles, Techniques, and Tools” (a. k. a, the “Dragon Book”)

Outline of coverage l Context-free grammars l Parsing – Tabular Parsing Methods – One pass • Top-down • Bottom-up l Yacc

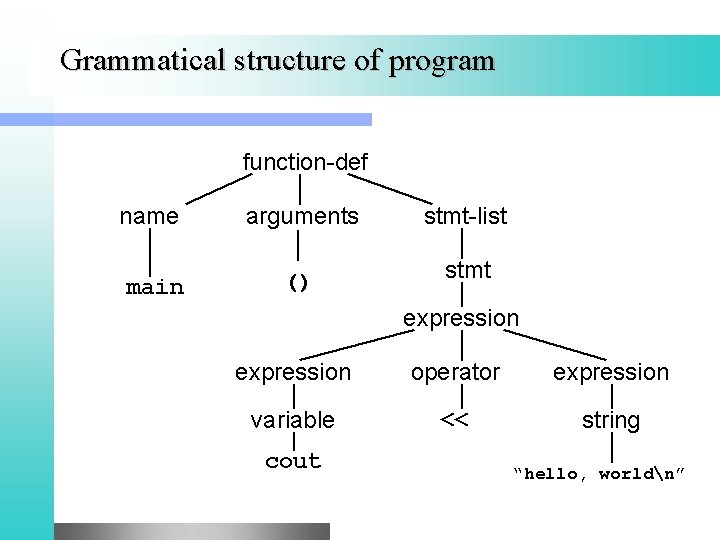
Grammatical structure of program function-def name arguments main () stmt-list stmt expression operator expression variable << string cout “hello, worldn”

Context-free languages Grammatical structure defined by contextfree grammar statement assignment ; statement expression ; statement compound-statement assignment ident = expression compound-statement { declaration-list statement-list } Definition (Context-free). Grammar with only one non -terminal symbol in left hand side of productions. Symbols terminal (token) non-terminal

Context Free Grammar G = (V, S, P, S) l V is a finite set of non-terminal symbols l S is a finite set of terminal symbols l P is a finite set of productions V (V S)* l S is the start symbol

Parse trees Parse tree: tree labeled with grammar symbols, such that: if node is labeled A and its children are labeled x 1. . . xn, then there is a production A x 1. . . xn l “Parse tree from A” = root labeled with A l “Complete parse tree” = all leaves labeled with tokens

Parse trees and sentences Frontier of tree = labels on leaves (in left-to -right order) l Frontier of tree from S is a sentential form l Definition. A sentence is the frontier of a complete tree from S. L E a L ; E “Frontier”

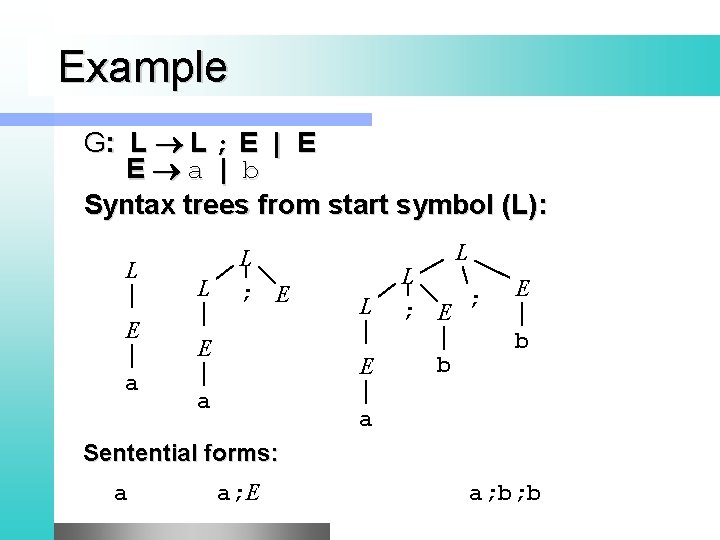
Example G: L L ; E | E E a | b Syntax trees from start symbol (L): L E a L L ; E E L L E a L ; E ; b E b a Sentential forms: a a; E a; b; b

Derivations Alternate definition of sentential form: l Given , in V*, say is a derivation step if ’ ’’ and = ’ ’’ , where A is a production l is a sentential form iff there exists a derivation (sequence of derivation steps) S (alternatively, we say that S * ) Two definitions are equivalent, but note that there are many derivations corresponding to each parse tre

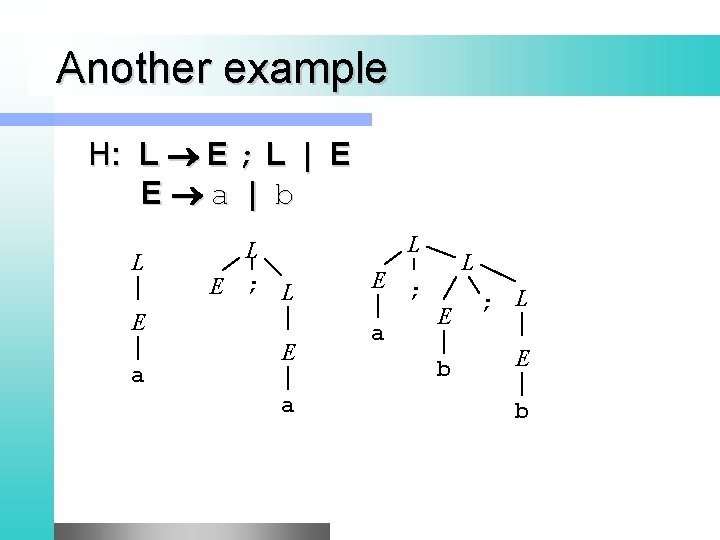
Another example H: L E ; L | E E a | b L L E ; L E a L E ; a L E b ; L E b

Ambiguity A sentence can have more than one parse tree l A grammar is ambiguous if there is a sentence with more than one parse tree l Example 1 E E+E | E*E | id l E E E + E id E * id E E id id E * E + E id id

Notes l If e then if b then d else f l { int x; y = 0; } l a. b. c = d; l Id -> s | s. id E -> E + T + T -> id + T -> id + T * id + T -> id + id * id + id

Ambiguity l Ambiguity is a feature of the grammar rather than the language l Certain ambiguous grammars may have equivalent unambiguous ones

Grammar Transformations l Grammars can be transformed without affecting the language generated l Three transformations are discussed next: – Eliminating Ambiguity – Eliminating Left Recursion (i. e. productions of the form A A ) – Left Factoring

Eliminating Ambiguity Sometimes an ambiguous grammar can be rewritten to eliminate ambiguity l For example, the grammar of Example 1 can be written as follows: l E E +T | T T E * id | id The language generated by this grammar is the same as that generated by the previous grammar. Both generate id(+id|*id)* l However, this grammar is not ambiguous l

Eliminating Ambiguity (Cont. ) l One advantage of this grammar is that it represents the precedence between operators. In the parsing tree, products appear nested within additions E E T id + T T * id id

Eliminating Ambiguity (Cont. ) l An example of ambiguity in a programming language is the dangling else l Consider S if then S else S | if then S |

Eliminating Ambiguity (Cont. ) l When there are two nested ifs and only one else. . S if b then S S else if b then S a S if b a S then if b then S a else S a

Eliminating Ambiguity (Cont. ) In most languages (including C++ and Java), each else is assumed to belong to the nearest if that is not already matched by an else. l This association is expressed in the following (unambiguous) grammar: l S Matched | Unmatched Matched if then Matched else Matched | Unmatched if then S | if then Matched else Unmatched

Eliminating Ambiguity (Cont. ) l Ambiguity is a property of the grammar l It is undecidable whether a context free grammar is ambiguous l The proof is done by reduction to Post’s correspondence problem l Although there is no general algorithm, it is possible to isolate certain constructs in productions which lead to ambiguous grammars

Eliminating Ambiguity (Cont. ) l For example, a grammar containing the production A AA | would be ambiguous, because the substring has two parses: A A A l A A A a a a A A A a a This ambiguity disappears if we use the productions A AB | B and B a or the productions A BA | B and B a.

Eliminating Ambiguity (Cont. ) l Examples of ambiguous productions: A A A | A A l A CF language is inherently ambiguous if it has no unambiguous CFG – An example of such a language is L = {aibjcm | i=j or j=m} which can be generated by the grammar: S AB | DC A a. A | C c. C | B b. Bc | D a. Db |

Elimination of Left Recursion l A grammar is left recursive if it has a nonterminal A and a derivation A + A for some string – l Top-down parsing methods cannot handle leftrecursive grammars, so a transformation to eliminate left recursion is needed Immediate left recursion (productions of the form A A ) can be easily eliminated: 1. Group the A-productions as A A 1 | A 2 | … | A m | 1| 2 | … | n where no i begins with A 2. Replace the A-productions by A 1 A’ | 2 A’ | … | n. A’ A’ 1 A’ | 2 A’| … | m. A’ |

Elimination of Left Recursion (Cont. ) l The previous transformation, however, does not eliminate left recursion involving two or more steps l For example, consider the grammar S Aa | b A Ac | Sd | e S is left-recursive because S Aa Sda, but it is not immediately left recursive

Elimination of Left Recursion (Cont. ) Algorithm. Left recursion elimination. Arrange nonterminals in some order A 1, A 2 , , …, An for i = 1 to n { for j = 1 to i - 1 { replace each production of the form Ai Aj by Ai d 1 | … | dn where Aj d 1 |…| dn are the current productions for Aj } eliminate the immediate left recursion among the Aiproductions }

Elimination of Left Recursion (Cont. ) Notice that iteration i only changes productions with Ai on the left-hand side, and Aj with j > i in the right-hand side l Correctness induction proof: l – Clearly true for i = 1 – If true for all i < k, then when the outer loop is executed for i = k, the inner loop will remove all productions Ai Aj with j < i – Finally, after the elimination of self recursion, m in any Ai Am productions will be > i l At the end of the algorithm, all derivations of the form Ai + Am will have m > i and therefore left recursion will not be present

Left Factoring Left factoring helps transform a grammar for predictive parsing l For example, if we have the two productions S if then S else S | if then S on seeing the input token if, we cannot immediately tell which production to choose to expand S l In general, if we have A 1 | 2 and the input begins with , we do not know (without looking further) which production to use to expand A l

Left Factoring (Cont. ) l However, we may defer the decision by expanding A to A’ l Then after seeing the input derived from , we may expand A’ to 1 or to 2 l Left-factored, the original productions become A A’ A’ 1 | 2

Non-Context-Free Language Constructs l Examples of non-context-free languages are: – L 1 = {wcw | w is of the form (a|b)*} – L 2 = {anbmcndm | n 1 and m 1 } – L 3 = {anbncn | n 0 } l Languages similar to these that are context free – L'1 = {wcw. R | w is of the form (a|b)*} (w. R stands for w reversed) This language is generated by the grammar S a. Sa | b. Sb | c – L'2 = {anbmcmdn | n 1 and m 1 } This language is generated by the grammar S a. Sd | a. Ad A b. Ac | bc

Non-Context-Free Language Constructs (Cont. ) l L''2 = {anbncmdm | n 1 and m 1 } is generated by the grammar S AB A a. Ab | ab B c. Bd | cd l L'3 = {anbn | n 1} is generated by the grammar S a. Sb | ab This language is not definable by any regular expression

CFG vs DFSA l L‘ 4 = {anbm | n > 0, n > 0} a start 0 b 1 b

Non-Context-Free Language Constructs (Cont. ) l l l Suppose we could construct a DFSM D accepting L'3. D must have a finite number of states, say k. Consider the sequence of states s 0, s 1, s 2, …, sk entered by D having read , a, aa, …, ak. Since D only has k states, two of the states in the sequence have to be equal. Say, si sj (i j). From si, a sequence of i bs leads to an accepting (final) state. Therefore, the same sequence of i bs will also lead to an accepting state from sj. Therefore D would accept ajbi which means that the language accepted by D is not identical to L’ 3. A contradiction.

Parsing The parsing problem is: Given string of tokens w, find a parse tree whose frontier is w. (Equivalently, find a derivation from w) A parser for a grammar G reads a list of tokens and finds a parse tree if they form a sentence (or reports an error otherwise) Two classes of algorithms for parsing: – Top-down – Bottom-up

Parser generators A parser generator is a program that reads a grammar and produces a parser l The best known parser generator is yacc It produces bottom-up parsers l Most parser generators - including yacc do not work for every CFG; they accept a restricted class of CFG’s that can be parsed efficiently using the method employed by that parser generator l

Top-down (predictive) parsing l Starting from parse tree containing just S, build tree down toward input. Expand left-most non-terminal.

Top-down parsing algorithm Let input = a 1 a 2. . . an current sentential form (csf) = S loop { suppose csf = a 1…ak. A based on ak+1…, choose production A csf becomes a 1…ak }

Top-down parsing example Grammar: H: L E ; L | E E a | b Input: a; b Parse tree Sentential form L L E ; L a Input L E; L a; b a; L a; b

Top-down parsing example (cont. ) Parse tree L E ; L a E b Input a; E a; b E L E ; L a Sentential form

LL(1) parsing l Efficient form of top-down parsing l Use only first symbol of remaining input (ak+1) to choose next production. That is, employ a function M: N P in “choose production” step of algorithm. l When this is possible, grammar is called LL(1)

LL(1) examples l Example 1: H: L E ; L | E E a | b Given input a; b, so next symbol is a. Which production to use? Can’t tell. H not LL(1)

LL(1) examples l Example 2: Exp Term Exp’ $ | + Exp Term id (Use $ for “end-of-input” symbol. ) Grammar is LL(1): Exp and Term have only one production; Exp’ has two productions but only one is applicable at any time.

Nonrecursive predictive parsing l Maintain a stack explicitly, rather than implicitly via recursive calls l Key problem during predictive parsing: determining the production to be applied for a non-terminal

Nonrecursive predictive parsing Algorithm. Nonrecursive predictive parsing Set ip to point to the first symbol of w$. Push S onto the stack. repeat Let X be the top of the stack symbol and a the symbol pointed to by ip if X is a terminal or $ then if X == a then pop X from the stack and advance ip else error() else // X is a nonterminal if M[X, a] == X Y 1 Y 2 … Y k then pop X from the stack push Yk. Y k-1, …, Y 1 onto the stack with Y 1 on top (push nothing if Y 1 Y 2 … Y k is ) output the production X Y 1 Y 2 … Y k else error() until X == $

LL(1) grammars l No left recursion A A : If this production is chosen, parse makes no progress. l No common prefixes A | Can fix by “left factoring”: A A’ ’ |

LL(1) grammars (cont. ) l No ambiguity Precise definition requires that production to choose be unique (“choose” function M very hard to calculate otherwise)

LL(1) definition l Define: Grammar G = (N, , P, S) is LL(1) iff whenever there are two left-most derivations S * w. A w * wtx S * w. A w * wty it follows that = Leftmost-derivation: where the leftmost non-terminal is always expanded first l In other words, given 1. a string w. A in V* and 2. t, the first terminal symbol to be derived from A there is at most one production that can be applied to A to yield a derivation of any terminal string beginning with wt

Checking LL(1)-ness For any sequence of grammar symbols , define set FIRST( ) to be FIRST( ) = { a | * a for some } l FIRST sets can often be calculated by inspection l

FIRST Sets Exp Term Exp’ $ | + Exp Term id (Use $ for “end-of-input” symbol) FIRST($) = {$} FIRST(+ Exp) = {+} FIRST($) FIRST(+ Exp) = {} grammar is LL(1)

FIRST Sets L E ; L | E E a | b FIRST(E ; L) = {a, b} = FIRST(E) FIRST(E ; L) FIRST(E) {} grammar not LL(1).

Computing FIRST Sets (no productions) Algorithm. Compute FIRST(X) for all grammar symbols X forall X V do FIRST(X) = {} forall X do FIRST(X) = {X} repeat forall productions X Y 1 Y 2 … Yk do FIRST(X) = FIRST(X) FIRST(Y 1) until no more elements are added to any FIRST set

Computing FIRST Sets (with productions) Algorithm. Compute FIRST(X) for all grammar symbols X forall X V do FIRST(X) = {} forall X do FIRST(X) = {X} forall productions X do FIRST(X) = FIRST(X) { } repeat forall productions X Y 1 Y 2 … Yk do for i = 1, k do FIRST(X) = FIRST(X) (FIRST(Yi) - { }) if FIRST(Yi) then break else if i == k then FIRST(X) = FIRST(X) { } until no more elements are added to any FIRST set

FIRST Sets of Strings of Symbols l FIRST(X 1 X 2…Xn) is the union of FIRST(X 1) and all FIRST(Xi) such that FIRST(Xk) for k = 1, 2, …, i-1 l FIRST(X 1 X 2…Xn) contains iff FIRST(Xk) for k = 1, 2, …, n

FIRST Sets do not Suffice l Given the productions A a. T x A b. T y T w T l T w should be applied when the next input token is w. l T should be applied whenever the next terminal is either x or y

FOLLOW Sets l For any nonterminal X, define the set FOLLOW(X) as FOLLOW(X) = {a | S * Xa }

Computing the FOLLOW Set Algorithm. Compute FOLLOW(X) for all nonterminals X FOLLOW(S) = {$} forall productions A B do FOLLOW(B) = Follow(B) (FIRST( ) - { }) repeat forall productions A B or A B with FIRST( ) do FOLLOW(B) = FOLLOW(B) FOLLOW(A) until all FOLLOW sets remain the same

Another Definition of LL(1) Define: Grammar G is LL(1) if for every A N with productions A 1 | | n FIRST( i FOLLOW(A)) FIRST( j FOLLOW(A)) = {} for all i, j

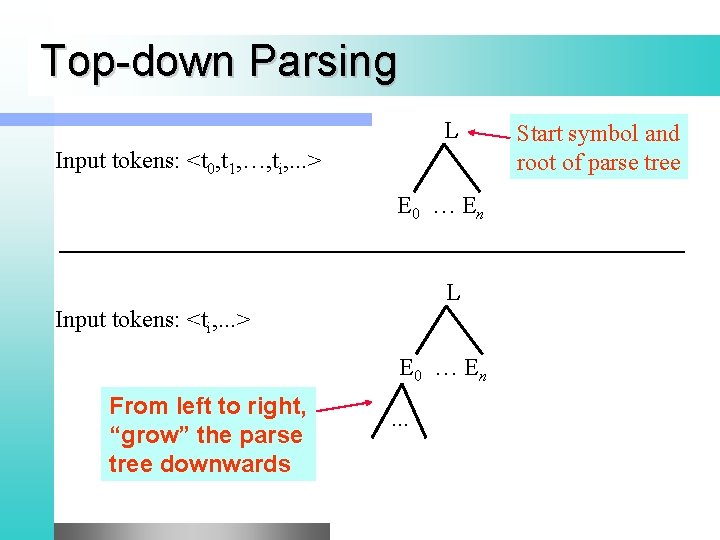
Top-down Parsing L Input tokens: <t 0, t 1, …, ti, . . . > E 0 … En L Input tokens: <ti, . . . > E 0 … En From left to right, “grow” the parse tree downwards . . . Start symbol and root of parse tree

Construction of a predictive parsing table Algorithm. Construction of a predictive parsing table M[, ] = {} forall productions A do forall a FIRST( ) do M[A, a] = M[A, a] {A } if FIRST( ) then forall b FOLLOW(A) do M[A, b] = M[A, b] {A } Make all empty entries of M be error

Recursive Descent Parsing

Recursive Descent Parser stat → var = expr ; expr → term [+ term] term → factor [* factor] factor → ( expr ) | var | constant | call( fun, expr ) var → identifier

Scanner public class Scanner { private Stream. Tokenizer input; private Type last. Token; public enum Type { INVALID_CHAR, NO_TOKEN , VARIABLE, PLUS, FALSE, TRUE, // etc. for remaining tokens, then: EOF }; } public Scanner (Reader r) { input = new Stream. Tokenizer(r); input. reset. Syntax(); input. eol. Is. Significant(false); input. word. Chars('a', 'z'); input. word. Chars('A', 'Z'); input. ordinary. Char('+'); input. ordinary. Char('*'); input. ordinary. Char('='); input. ordinary. Char('('); input. ordinary. Char(')');

Scanner } public Type next. Token() { try { switch (input. next. Token()) { case Stream. Tokenizer. TT_EOF: return EOF; case Type. TT_WORD: if (input. sval. equals("false")) return FALSE; else if (input. sval. equals("true")) return TRUE; else return VARIABLE; case '+': return PLUS; break; // etc. } } catch (IOException ex) { return EOF; } }

Parser public class Parser { private Scanner scanner; private Type token; public Expr parse(Reader r) throws Syntax. Exception { scanner = new Scanner(r); next. Token(); // assigns token Statement stat = statement(); expect(scanner. EOF); return stat; }

Statement // stat : : = variable '=' expr '; ' private Statement stat() throws … { Variable var = variable(); expect(scanner. ASSIGN); Expr exp = expr(); Statement stat = new Statement(var, exp); expect(scanner. SEMICOLON); return stat; }

class Statement { Variable var; Expr expr; Statement(Variable v, Expression e) { this. var = v; this. expr = e; } … }

interface Expression { int eval(); String print(); } class Variable implements Expression { String print() { return name; } String name; Variable(String name) {this. name = name); } } class Expr extends Expression … class Term extends Expression… class Factor exteds Expression …

class Term extends Expression { Expression first; Term rest; String print() { String res = first. print(); if (rest != null) res += “ + rest. print(); return res; }

int eval() { int res = first. eval(); if (rest != null) res += rest. eval(); return res; }

Expr // expr : : = term ['+' term] private Expr expr() throws … { Term exp = term(); while (token == scanner. PLUS) { next. Token(); exp = new Term(exp, term()); } return exp; }

Term // term : : = factor ['*' term ] private Term term() throws Syntax. Exception { Term exp = factor(); // Rest of body: left as an exercise. }

Factor // factor : : = ( expr ) | var private Factor factor() throws Syntax. Exception { Factor exp = null; if (token == scanner. LEFT_PAREN) { next. Token(); exp = expr(); expect(scanner. RIGHT_PAREN); } else { exp = variable(); } return exp; }

Variable // variable : : = identifier private Variable variable() throws Syntax. Exception { if (token == scanner. ID) { Variable exp = new Variable(input. get. String()); next. Token(); return exp; } }

Constant private Expr constant. Expression() throws Syntax. Exception { Expr exp = null; // Handle the various cases for constant // expressions: left as an exercise. return exp; }

Utilities private void expect(Type t) throws Syntax. Exception { if (token != t) throw Syntax. Exception. . . next. Token(); } } private void next. Token() { token = scanner. next. Token(); }

Exercise l Write a RD parser for JSON

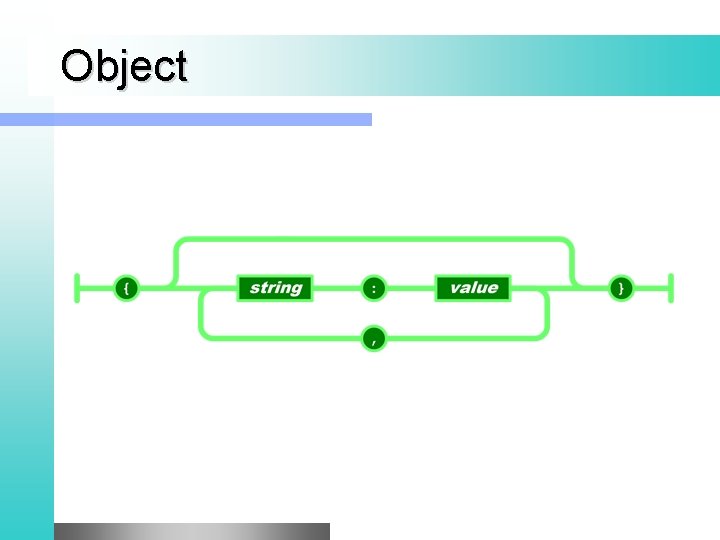
Object

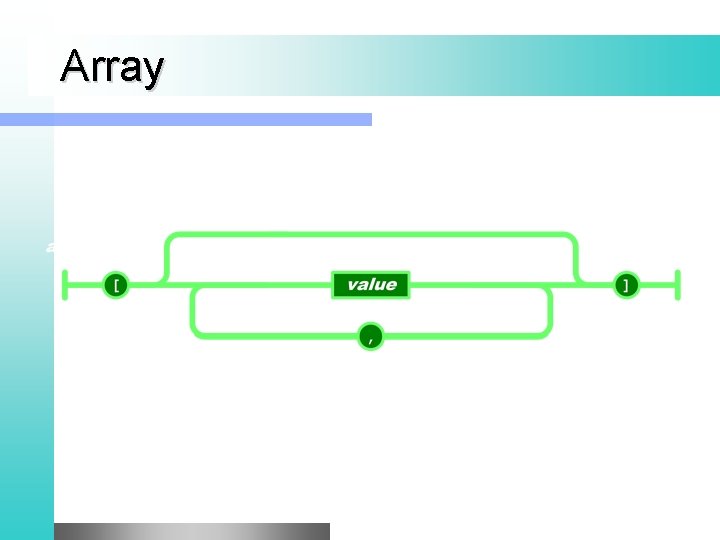
Array

Example { "name": { "first": "John", "last": "Doe" }, "age": 23, "children": ["Paul", "Mary"] }

Recursive Descent in practice l RD parser are quite used in practice even for real programming languages l GCC uses an hand-written RD parser for both C and C++ l Clang uses RD for parsing C l V 8 uses RD for Java. Script l Ocaml and Haskell use LALR(1) parser generators

Pascal Syntax Diagrams

Regular Languages

Regular Languages l Definition. A regular grammar is one whose productions are all of the type: A a. B A a l A Regular Expression a R 1 | R 2 R 1 R 2 R* is either:

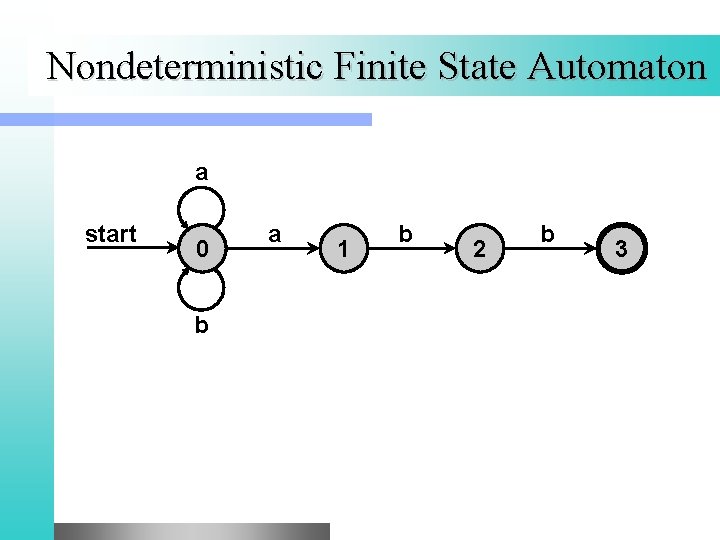
Nondeterministic Finite State Automaton a start 0 b a 1 b 2 b 3

Regular Languages l Theorem. The classes of languages – Generated by a regular grammar – Expressed by a regular expression – Recognized by a NDFS automaton – Recognized by a DFS automaton coincide.

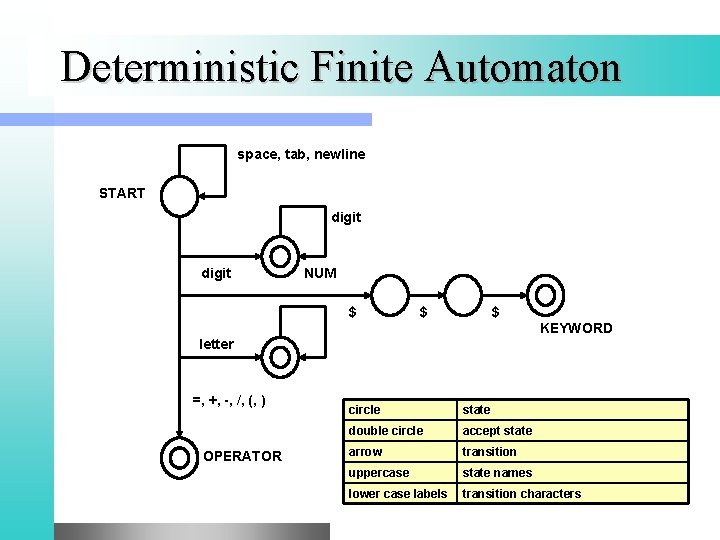
Deterministic Finite Automaton space, tab, newline START digit NUM $ $ $ KEYWORD letter =, +, -, /, (, ) OPERATOR circle state double circle accept state arrow transition uppercase state names lower case labels transition characters

Scanner code state : = start loop if no input character buffered then read one, and add it to the accumulated token case state of start: case input_char of A. . Z, a. . z : state : = id 0. . 9 : state : = num else. . . end id: case input_char of A. . Z, a. . z : state : = id 0. . 9 : state : = id else. . . end num: case input_char of 0. . 9: . . . end;

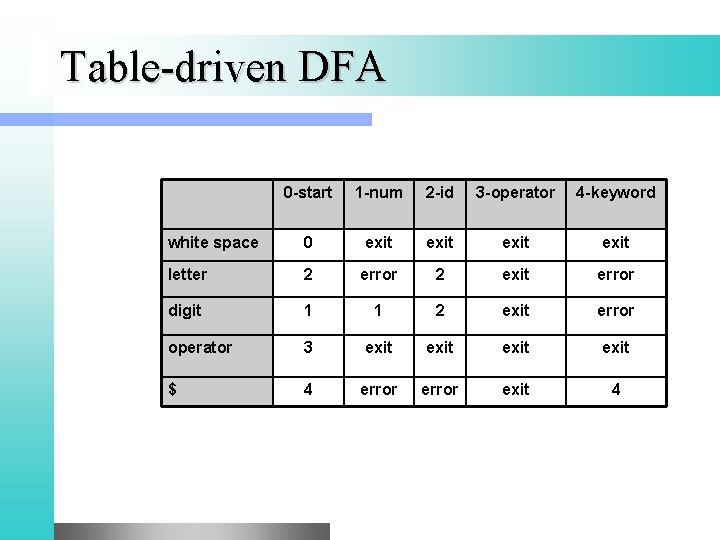
Table-driven DFA 0 -start 1 -num 2 -id 3 -operator 4 -keyword white space 0 exit letter 2 error 2 exit error digit 1 1 2 exit error operator 3 exit $ 4 error exit 4

Language Classes L 0 CSL CFL [NPA] LR(1) LL(1) RL [DFA=NFA]

Question l Are regular expressions, as provided by Perl or other languages, sufficient for parsing nested structures, e. g. XML files?

Exercise ( E + 0) -> E ( E * 1) -> E (E * 0) -> 0 ( a + ( b * 0)) => a s/pattern/replacement/ s/( (. *) * 0)/0/