Recursive descent parsing Some notes on recursive descent

Recursive descent parsing

Some notes on recursive descent n The starter code that I gave you did not exactly fit the grammar that I gave you n n Both work, both are correct Many things can be coded either recursively or iteratively n I gave you an iterative grammar and recursive code

Recursive rule for <term> n n <term> : : = <factor> <multiply_operator> <term> public boolean term() { if (!factor()) return false; if (!multiply. Operator()) return true; if (!term()) error("No term after '*' or '/' "); return true; }

Iterative rule for <term> n n <term> : : = <factor> { <multiply_operator> <factor> } public boolean term() { if (!factor()) return false; while (multiply. Operator()) { if (!factor()) error("No factor after '*' or '/' "); } return true; }

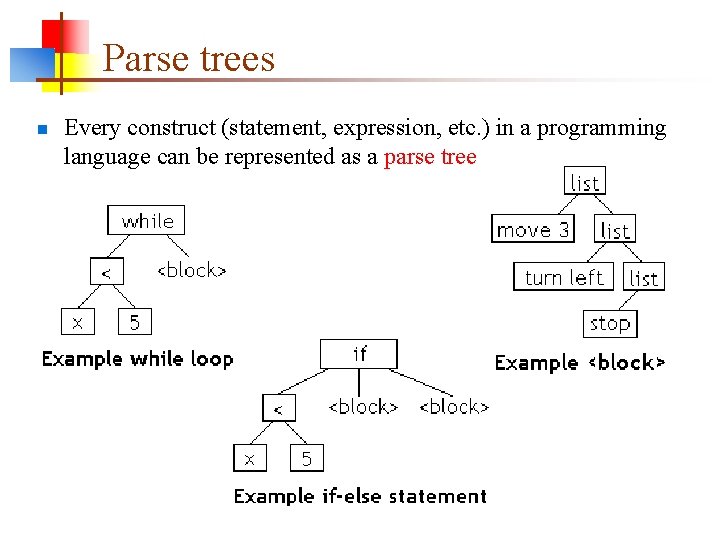
Parse trees n Every construct (statement, expression, etc. ) in a programming language can be represented as a parse tree

Recognizers and parsers n n n A recognizer tells whether a given string “belongs to” (is correctly described by) a grammar A parser uses a grammar to construct a parse tree from a given string One kind of parser is a recursive descent parser n Recursive descent parsers have some disadvantages: n n And some advantages: n n n They are not as fast as some other methods It is difficult to provide really good error messages They cannot do parses that require arbitrarily long lookaheads They are exceptionally simple They can be constructed from recognizers simply by doing some extra work —specifically, building a parse tree Recursive descent parsers are great for “quick and dirty” parsing jobs

The Stack n One easy way to do recursive descent parsing is to have each parse method take the tokens it needs, build a parse tree, and put the parse tree on a global stack n Write a parse method for each nonterminal in the grammar n n n Each parse method should get the tokens it needs, and only those tokens n Those tokens (usually) go on the stack Each parse method may call other parse methods, and expect those methods to leave their results on the stack Each (successful) parse method should leave one result on the stack

Example: while statement n n <while statement> : : = “while” <condition> <block> The parse method for a while statement: n n n Calls the Tokenizer, which returns a “while” token Makes the “while” into a tree node, which it puts on the stack Calls the parser for <condition>, which parses a condition and puts it on the stack n n “while” <condition> (“top” is on right) Calls the parser for <block>, which parses a block and puts it on the stack n n Stack now contains: “while” <condition> <block> Pops the top three things from the stack, assembles them into a tree, and pushes this tree onto the stack

Recognizing a while statement n // <while statement> : : = “while” <condition> <block> private boolean while. Statement() { if (keyword("while")) { if (condition()) { if (block()) { return true; } else error("Missing '{' "); } else error("Missing <condition>"); } return false; } Why do you suppose I named this method while. Statement() instead of while() ?

Parsing a while statement n n n // <while statement> : : = “while” <condition> <block> private boolean while. Statement() { if (keyword("while")) { if (condition()) { if (block()) { make. Tree(3, 2, 1); return true; } else error("Missing '{' "); } else error("Missing <condition>"); } return false; } This code assumes that keyword(String), condition(), and block() all leave their results on a stack On the stack, while = 3, <condition> = 2, <block> = 1

Alternative code n n public boolean while. Statement() { if (keyword("while") && condition() && block()) { make. Tree(3, 2, 1); return true; } return false; } No room for an error condition in this code

Alternative code with one message n public boolean while. Statement() { if (keyword("while")) { if (condition()) && (block()) { make. Tree(3, 2, 1); return true; } error("Error in "while" statement"); } return false; }

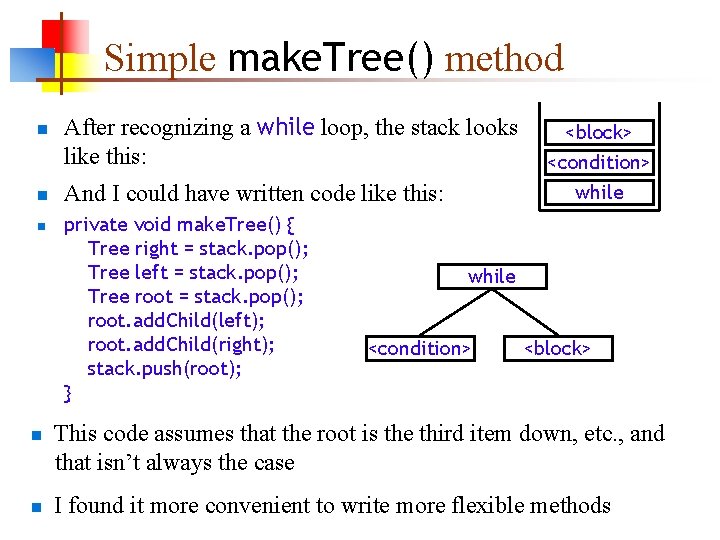
Simple make. Tree() method n n n After recognizing a while loop, the stack looks like this: And I could have written code like this: private void make. Tree() { Tree right = stack. pop(); Tree left = stack. pop(); Tree root = stack. pop(); root. add. Child(left); root. add. Child(right); stack. push(root); } <block> <condition> while <condition> <block> This code assumes that the root is the third item down, etc. , and that isn’t always the case I found it more convenient to write more flexible methods

More general make. Tree method n private void make. Tree(int keyword, int left, int right) { Tree root = get. Stack. Item(keyword); Tree left. Child = get. Stack. Item(left); Tree right. Child = get. Stack. Item(right); stack. pop(); } root. add. Child(left. Child); root. add. Child(right. Child); stack. push(root);

Parser methods n In the BNF, I have one long definition for <command> n n <command> : : = <move> <expression> <eol> | "turn" <direction> <eol> | "take" <object> <eol> | "drop" <object> <eol>. . . In my code, I broke that into multiple methods n <command> : : = <move command> | <turn command> | <take command> | <drop command>. . .

My command() method n public boolean command() { if (move()) return true; if (turn()) return true; if (take()) return true; if (drop()) return true; . . . return false; }

Helper methods n n I wrote a number of helper methods for the Parser and for the Parser. Test classes It’s helpful to have methods to build trees quickly and easily n n Another useful method is assert. Stack. Top, which is just n n private make. Tree(String op) private Tree make. Tree(String op, Tree left, Tree right) Java 5 allows a variable number of arguments, so you could write private Tree make. Tree(String op, Tree. . . children) private void assert. Stack. Top(Tree expected) { assert. Equals(expected, parser. stack. peek()); } Example: n Tree condition = make. Tree("=", "2"); assert. Stack. Top(make. Tree("if", condition, "list"));

Final comments n You are welcome to use any of this code, but. . . n n n . . . my code is never the last word on anything! Code can always be improved While I think my code is generally useful, you always have to understand it well enough to adapt it to your particular needs

The End