Metody Matematyczne w Inynierii Chemicznej wykad 1 Literatura

Metody Matematyczne w Inżynierii Chemicznej wykład 1

Literatura w Emil Slavicek, Technika obliczeniowa dla chemików, WNT Warszawa 1991 w Anthony Ralston, Wstęp do analizy numerycznej w Karol Machej, Elementy programowania w języku BASIC i Pascal, skrypt 1833 w William Volk, Statystyka stosowana dla inżynierów WNT Warszawa 1965

Czym są metody numeryczne? w Dział matematyki zajmujący się rozwiązywaniem problemów matematycznych za pomocą operacji ARYTMETYCZNYCH. w Wykorzystuje się przybliżenia wielkości niearytmetycznych arytmetycznymi i badanie błędów tego przybliżenia.

Błąd - definicja w Wartość dokładna=wartość przybliżona+Błąd względny=błąd/wartość dokładna

BŁĘDY OBLICZENIOWE 1. 2. 3. 4. Błąd zaokrąglenia Błąd metody Błąd obcięcia Inne błędy

1. Błąd zaokrąglenia Dokładnie można przedstawić tylko liczby całkowite i wymierne. Liczby niewymierne i o nieskończonym rozwinięciu dziesiętnym zawsze zapisujemy z błędem bo używamy skończonej ilości cyfr. Wymierne często też skracamy Przykład Używając 5 miejsc znaczących Popełniamy błąd zaokrąglenia

Błąd - definicja w Przedstawiając 1/3 w zapisie dziesiętnym jako 0, 333

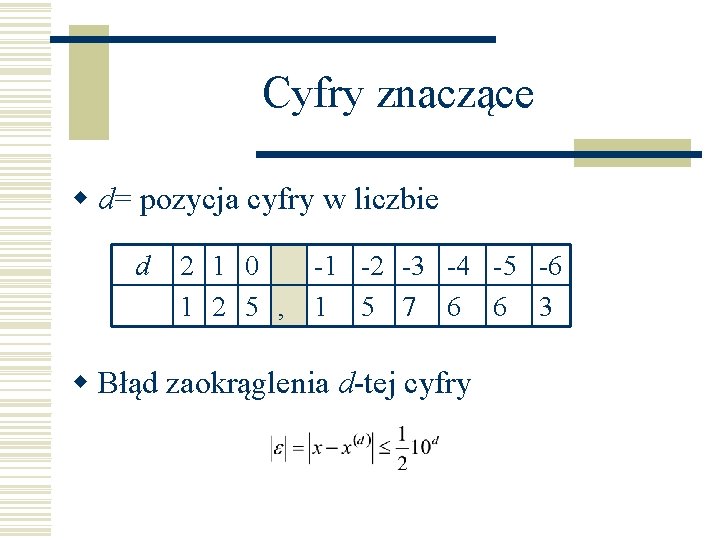
Cyfry znaczące w d= pozycja cyfry w liczbie d 2 1 0 1 2 5 , -1 -2 -3 -4 -5 -6 1 5 7 6 6 3 w Błąd zaokrąglenia d-tej cyfry

Cyfry znaczące w Cyfrę na pozycji k-tej nazywamy znaczącą jeżeli dla przybliżenia y dokładnej liczby x k 2 1 0 -1 -2 50 5 0, 05 , 005 -3 -4 0, 0005 0, 00005 w Dla poprawnych zaokrągleń znaczące są wszystkie cyfry zaokrąglenia

Cyfry znaczące w x=1, 264578985422 w y=1, 2646 w k 0 -1 -2 0, 5 0, 05 , 005 -3 -4 -5 0, 00005 0, 000005

Cyfry znaczące w Ilość cyfr znaczących n jest miarą błędu względnego w Istotny jest wzrost błędu względnego przy odejmowaniu liczb podobnych

2. Błąd metody Jego przyczyna leży w niedoskonałości metod obliczeniowych, n n Zastosowania skończonych przyrostów w miejsce nieskończenie małych. Zastosowanie funkcji przybliżających w miejsce rzeczywistych

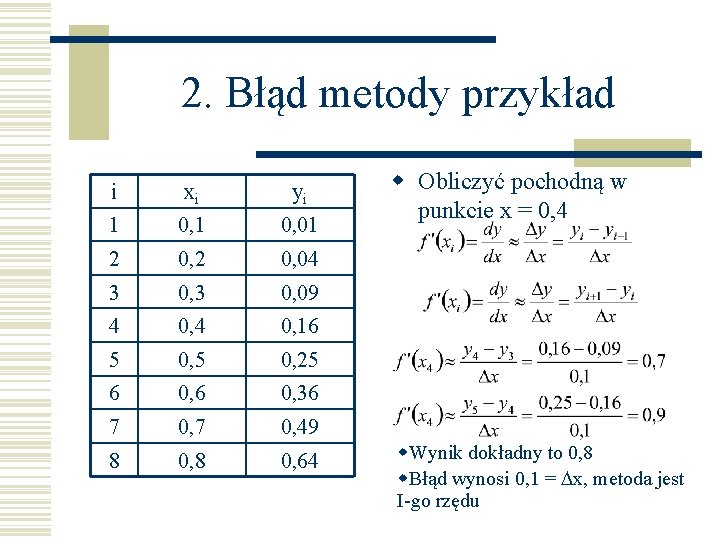
2. Błąd metody przykład i xi yi 1 0, 01 2 0, 04 3 0, 09 4 0, 16 5 0, 25 6 0, 36 7 0, 49 8 0, 64 w Obliczyć pochodną w punkcie x = 0, 4 w. Wynik dokładny to 0, 8 w. Błąd wynosi 0, 1 = x, metoda jest I-go rzędu

3. Błąd obcięcia w Dotyczy: n n iteracyjnych metod obliczeniowych (w których do rozwiązania zbliżamy się powtarzając obliczenia) usunięcia mniej znaczących wyrazów (np. w rozwinięciu w szereg) w Do wyniku dokładnego: n n w metodach iteracyjnych dochodzi się po nieskończonej ilości powtórzeń a praktycznie obliczenia trzeba w pewnym momencie zakończyć Stosując nieskończoną ilość wyrazów

3. Błąd obcięcia Przykład: znaleźć pierwiastek równania xwynik i = i +1

3. Błąd obcięcia Rozwinięcie w szereg Taylora ograniczmy się do k=1 n = 1, h = x, x = xi, x+nh = xi+1

3. Błąd obcięcia Dokładniejszy wzór uzyskamy stosując 3 wyrazy w rozwinięciu w szereg Taylora (k=2)

3. Błąd obcięcia Stosując zapis skrócony: Stosując powyższy wzór do przykładu

4. Inne błędy - błąd systematyczny w Związany jest z niedokładnymi wskazaniami przyrządów pomiarowych w Każdy przyrząd pomiarowy ma określoną dokładność nazwaną klasą dokładności. w Błąd E wskazań przyrządu oblicza się mnożąc skalę S przez klasę K i dzieląc przez 100

4. Inne błędy - błąd systematyczny Przykład: manometr ma zakres 250 bar i klasę 2, 5. W jakich granicach mieści się zmierzone za jego pomocą ciśnienie Oznacza to, że jeżeli manometr wskazał ciśnienie 100 bar to rzeczywiste ciśnienie mieści się w przedziale <93, 75; 106, 25>

Inne błędy w Błąd przypadkowy w Błąd gruby

ALGORYTM DEFINICJA w Algorytm jest to jednoznaczny przepis pozwalający na wykonanie postawionego zadania. Ma następujące cechy: 1. 2. 3. Określoność (dostateczna szczegółowość i jednoznaczność)– nie ma w nim dowolności, czyli przypadkowego postępowania. Rezultat nie może zależeć od osoby realizującej algorytm. Ogólność – pozwala rozwiązać klasę zadań a nie tylko jedno szczególne zadanie. Np. za algorytm można uznać przepis na sumowanie dwóch liczb a nie taki, który dodaje 2 i 2. Efektywność – oznacza, że po wykonaniu skończonej i możliwie najmniejszej ilości operacji otrzymuje się poprawny wynik i to w czasie, w którym można go praktycznie wykorzystać.

Schemat blokowy DEFINICJA w Schemat blokowy to graficzny obraz struktury algorytmu. Składa się z określonych (znormalizowanych) znaków i symboli graficznych (tzw. bloków) połączonych liniami. Kolejność wykonywania określają linie łączące bloki, od góry na dół i od lewej do prawej, chyba że strzałki stanowią inaczej. Pierwszym elementem jest zawsze blok START, a ostatnim KONIEC. Operacje wykonywane w danym elemencie wpisuje się wewnątrz bloku.

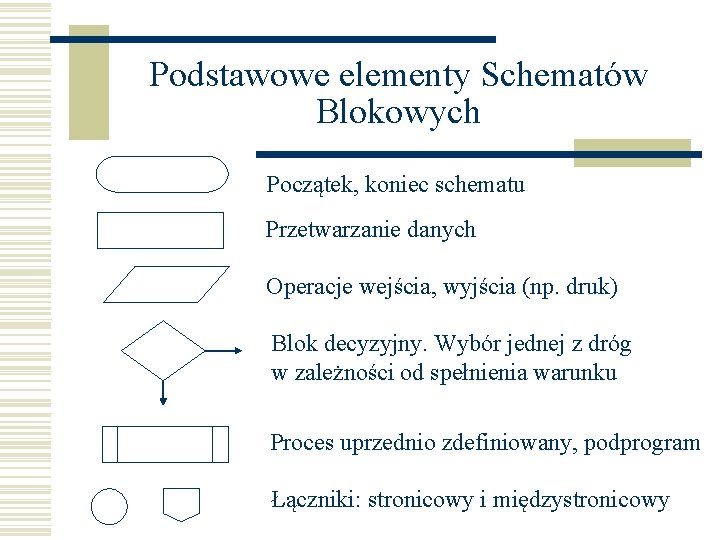
Podstawowe elementy Schematów Blokowych Początek, koniec schematu Przetwarzanie danych Operacje wejścia, wyjścia (np. druk) Blok decyzyjny. Wybór jednej z dróg w zależności od spełnienia warunku Proces uprzednio zdefiniowany, podprogram Łączniki: stronicowy i międzystronicowy

Metody Matematyczne w Inżynierii Chemicznej Algorytmy iteracyjne

Algorytmy iteracyjne - definicja Jest to klasa algorytmów, w których występuje powtarzanie pewnych kroków obliczeń w wyniku czego otrzymuje się rozwiązanie z dokładnością rosnącą wraz z liczbą powtórzeń. Całkowicie dokładny wynik uzyskuje się po nieskończonej liczbie powtórzeń (iteracji).

Przykład – algorytm obliczania pierwiastka liczby N>0

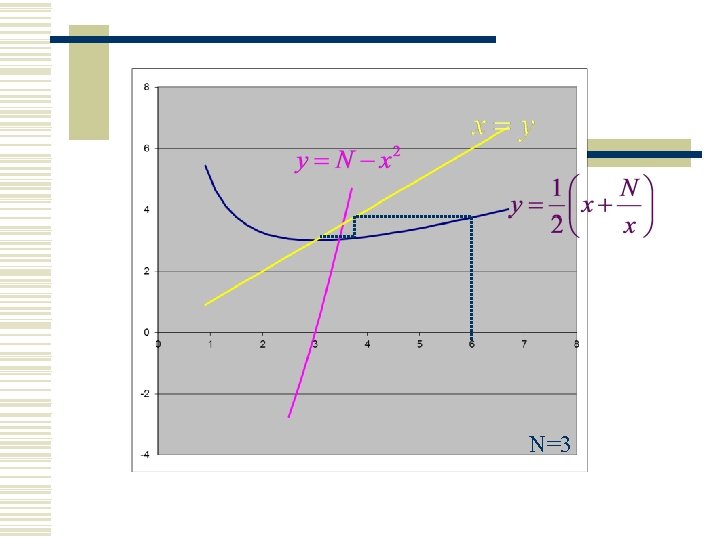
Przykład – algorytm obliczania pierwiastka liczby N>0 Wzór iteracyjny: Obliczyć pierwiastek z 9. Jako pierwsze przybliżenie przyjąć x 0 = 6.

N=3

Podstawy teoretyczne procesów iteracyjnych Rozważmy zadanie typu: Pierwszy krok to przekształcenie do postaci Z której wynika: Od kolejnych wartości xk oczekuje się, by spełniały warunek: rozwiązanie dokładne

Podstawy teoretyczne procesów iteracyjnych Inaczej można to wyrazić wzorem: Aby algorytm można uznać za algorytm iteracyjny to przekształcenie Musi dawać zbieżny ciąg wartości xk.

Podstawy teoretyczne procesów iteracyjnych Warunek zbieżności wyrażony za pomocą błędu k-tego kroku

Szybkość zbieżności procesu iteracyjnego Związek miedzy ek+1 i ek Rozwijając funkcję F(x) w szereg Taylora wokół punktu xk na promieniu h = ek można wyprowadzić zależność na zmianę błędu w kolejnym kroku. Z definicji błędu:

Szybkość zbieżności procesu iteracyjnego Z definicji przekształcenia iteracyjnego: Podstawiając do rozwinięcia w szereg:

Szybkość zbieżności procesu iteracyjnego Wprowadzając oznaczenie: Zakładając, że ek jest bardzo małe, znaczenie ma ten wyraz, dla którego parametr b jest różny od 0 przy najmniejszej potędze ek Z praktycznego punktu widzenia rozpatruje się tylko potęgi od 1 - 3

Szybkość zbieżności procesu iteracyjnego 1. Jeżeli b 1 0, błędy w dwu kolejnych krokach wiąże zależność liniowa: Iteracja pierwszego rzędu 2. Jeżeli b 1 = 0 i b 2 0 , błędy w dwu kolejnych krokach wiąże zależność paraboliczna: Iteracja drugiego rzędu

Szybkość zbieżności procesu iteracyjnego 3. Jeżeli b 1 = 0 i b 2 = 0 a b 3 0 , błędy w dwu kolejnych krokach wiąże zależność: Iteracja trzeciego rzędu Ponieważ ek<1 to im większy rząd metody tym jest ona szybciej zbieżna

Warunki zbieżności procesu iteracyjnego w zależności od jego rzędu Aby proces iteracyjny był zbieżny dla dowolnego kroku k większego od pewnego kroku p musi być spełniony warunek: 1. Proces pierwszego rzędu lub

Warunki zbieżności procesu iteracyjnego W przypadku metod rzędu I-go jedynym warunkiem zbieżność jest by moduł pochodnej F’(x) w punkcie startowym był mniejszy od 1.

Warunki zbieżności procesu iteracyjnego 2. Proces drugiego rzędu lub W warunku zbieżności występuje wartość błędu. Ponieważ jest ona nieznana nie dla wszystkich punktów startowych będzie on mniejszy od granicznego ep dlatego obliczenia mogą nie być zbieżne!

Warunki zbieżności procesu iteracyjnego 3. Proces iteracyjny trzeciego rzędu Podobnie jak w przypadku II-go rzędu osiągnięcie zbieżności zależy od przyjętego punktu startowego

Praktyczny warunek zakończenia obliczeń Ponieważ rzeczywista wartość błędu jest nieznana jako warunek kończący obliczenia przyjmuje się zależność opartą o różnicę rozwiązania obliczonego w dwóch kolejnych krokach e - założona wartość określająca dokładność obliczeń Wykorzystuje się ją w algorytmie, do sformułowania warunku kończącego pętlę iteracyjną

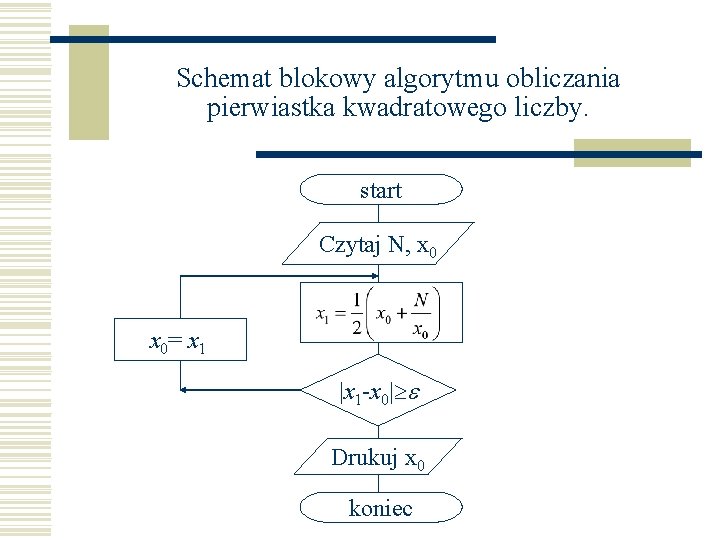
Schemat blokowy algorytmu obliczania pierwiastka kwadratowego liczby. start Czytaj N, x 0= x 1 |x 1 -x 0| e Drukuj x 0 koniec

Związek między e i e. Ile wynosi błąd w momencie zakończenia obliczeń iteracyjnych? Iteracja pierwszego rzędu:

Związek między e i e. Jeżeli b 1 jest bliskie 1 to błąd jest znacząco większy e. Np. dla b 1 = 0, 9

Związek między e i e. Iteracje wyższych rzędów Z warunku zbieżności: Można zaniedbać w różnicy

Związek między e i e. Dla iteracji wyższych błędów rzeczywisty błąd obliczeń ek jest zwykle co najmniej o rząd wielkości mniejszy od parametru e decydującego o zakończeniu obliczeń.