Markov Processes Markov Chains 1302022 rd 1 Lagrange

Markov Processes Markov Chains 1/30/2022 rd 1

Lagrange Multipliers You need 100 units made at 2 plants with the total cost function C = 0. 1 x 2 + 7 x + 15 y + 1000. How should you divide the units between plants x and y to minimize the cost? L(x, y, ) = 0. 1 x 2 + 7 x + 15 y +1000 + (x + y – 100) Lx = 0. 2 x + 7 + = 0 Ly = 15 + = 0 => = -15 and 0. 2 x + 7 = 15 or x = 40; y = 60. (solve '((. 2 0 1 -7)(0 0 1 -15)(1 1 0 100))) (40 60 -15) C(40, 60) = $2349 min. See that Lxx and Lyy are > 0; D > 0 1/30/2022 rd 2

Examples System Market share States Transition p's Brand A vs. Brand B Switch chances TV Market Proportion watching 2 Switch chances Rental returns to various locations Machine breakdowns 1/30/2022 % not running rd different returns p of running 3

Markov Process Describes a dynamic situation and predicts the movement of a system along different states as time passes. bus F car From To T bus 0. 2 0. 4 [ ¼ ¾ ] column vector car 0. 8 0. 6 ( ¼ ¾ ) row vector Presently initial state vector is a 0 0. 3 0. 7 for (bus, car) Tij = P(next state is i | current state is j Tbus car = P(riding bus | after riding car) = 0. 4 e 1/30/2022 rd 4

Markov Assumptions Finite number of states (none absorbing) State in any period depends only on previous State Transition probabilities are constant over time Changes occur only once during period Transition periods occur with regularity Initial state a 0 for example is [0. 275 0. 350] sum to 1 T T 2 T 3 T 4 … are the powers of T and approach the fixed point. State Transition Matrix States 1 2 3 1 0. 2 0. 3 0. 4 2 0. 4 0. 5 0. 2 3 0. 4 0. 2 0. 4 Column vectors are probability vectors Tij = P(next state is i | current state is j); T 21 = 0. 4 1/30/2022 rd 5

Markov States Transient- a state when entered, can never return to this state when out and about. Recurrent - a state when entered, process will definitely return to this state. Absorbing - when entered, will never leave again. States are either recurrent or transient. 1/30/2022 rd 6

Fixed Point A B if Tx = x fixed point A 0. 2 0. 3 then T x = x is also a fixed point B 0. 8 0. 7 0. 2 a + 0. 3 b = a or 0. 8 a + 0. 7 b = b; or 0. 8 a – 0. 3 b = 0 a+b=1 (solve '((4/5 -3/10 0)(1 1 1))) (3/11, 8/11) Steady state solution which is the Limit of the Matrix as n (setf mat. T #2 A((0. 2 0. 3)(0. 8 0. 7))) (setf fm (expt-matrix mat. T 10) #2 A((0. 2727)(0. 7273)) (M* fm #2 A((1)(0))) #2 A((0. 272727)(0. 727273)) Multiply the limit matrix by any probability vector results in fixed vector. 1/30/2022 rd 7

Eigenvalues Given matrix ¼ ½ ¾ ½ TX = t. X => (t. I – T)X = 0 3/4 x – 1/2 y = 0 (quadratic 1 -3/4 -1/4) (1 -1/4) are the eigenvalues (eigenvalues #2 A((1/4 1/2)(3/4 1/2))) (-0. 25 1) Eigenvectors are (2, 3) and (1, -1) (M* #2 a((1/4 1/2)(3/4 1/2)) #2 A((2)(3))) #2 A((2)(3)) (M* #2 a((1/4 1/2)(3/4 1/2)) #2 A((1)(-1))) #2 A((-1/4)(1/4)) (expt-matrix #2 A((0. 25 1/2))(3/4 1/2)) 30) #2 A((0. 4)(0. 6)) (M* (inverse #2 A((2 1)(3 -1))) #2 A((1/4 1/2)(3/4 1/2)) #2 A((2 1)(3 -1))) #2 A((1 0)(0 -1/4)) 1/30/2022 rd 8

Eigenvalues A=1 4 Ax = tx => t-1 -4 2 3 -2 t-3 = t 2 -4 t -5 = 0; (5, -1) Eigenvectors: 4 x - 4 y = 0 or x = y [1 1] -2 x - 4 y = 0 or x = 2 y [2 -1] (M* #2 a((1 4)(2 3)) #2 a((1)(1))) #2 A((5)(5)) ~ (1, 1) (M* #2 a((1 4)(2 3)) #2 a((2)(-1))) #2 A((-2)(1)) Diagonalize (M* (inverse #2 a((1 2)(1 -1))) #2 a((1 4)(2 3)) #2 a((1 2)(1 -1))) #2 A((5 0)(0 -1)) Give another value in lieu of [2 -1]. 1/30/2022 rd 9

Toothpaste G C G owns 60% (a 0 = 0. 6 0. 4] of market and T = 0. 88 0. 15 0. 12 0. 85 in that 88% of G's customers remain loyal and 15% of those using the competitors brands switch to G. (eigenvalues #2 A((0. 88 0. 15)(0. 12 0. 85))) (0. 73 1) (expt-matrix #2 A((0. 88 0. 15)(0. 12 0. 85)) 50) (5/9, 4/9) (M* (inverse #2 A((0. 12 -0. 15)(-0. 12))) #2 A((0. 88 0. 15) (0. 12 0. 85)) #2 A((0. 12 -0. 15)(-0. 12))) #2 A((0. 73 0)(0 1. 0)) (-0. 15 -0. 12) (0. 12 - 0. 12) is eigenvector; 15/27 = 0. 55555 #2 A((0. 555556)(0. 444445)) a 0 = (0. 6 0. 4). a 1 = Ta 0 ; an = Tna 0 Note that dominant eigenvalue is 1 and determines the stability eigenvector. The dominant eigenvalue is always 1 for a transition matrix 1/30/2022 rd 10

Degenerate Discrete-Parameter Stochastic Process T= 0 1 1 0 Solve to get a = b = ½ but Tn = 0 1 1 0 Process is strictly stationary and time-independent. Consider T = ½ ½ a + b = 2 a ½ ½ a + b = 1 => (a, b) = (½, ½) Consider T = Tn = 1/3 2/3 1/30/2022 1 a + 2 b = 3 a => a = b 1 a + 1 b = 1 or (½, ½) rd 11

Stochastic Matrix A matrix is stochastic if its columns (rows) are probability vectors and is called a regular matrix if some power of the matrix has positive vector components. ½ ¼ is regular ½ ¾ Regular matrices have a unique fixed probability vector with positive components and The powers of the regular matrices approach the fixed point. If A and B are stochastic, then the product AB is also. 1/30/2022 rd 12

Stochastic and Regular Matrices Fixed points of square matrices Let A = |2 2| and u = [2, -1] |1 3| Then |2 2|| 2 |= | 2| |1 3||-1 | |-1| Also A(tu) = t. Au => tu or scalar multiples are fixed points. Matrix is ergodic if limit exists; regular if any power has plus entries (expt-matrix #2 A((2 2)(1 3)) 20) NOT ergodic, - 2 -2 -1 - 3 yields 2 - 5 + 4 = 0; with eigenvalues = -1, -4; (expt-matrix #2 A((. 25. 75)(. 75. 25)) 20) #2 A((0. 5)) ergodic - ¼ -¾ -¼ - ¾ yields 2 - = 0; = 0, 1 (solve '((1 1 1)(1 -0. 4 0))) (0. 285714 0. 714286) = (2/7, 5/7) 1/30/2022 rd 13

Stochastic and Ergodic Consider matrix A and Ax = x where x = (a b) a/2 + 2 b/3 = a 3 a - 4 b = 0 1 a +1 b = 1 (solve '((3 -4 0)(1 1 1))) (4/7 3/7) (expt-matrix #2 A ((0. 5 0. 67)(0. 5 0. 33)) 20) Limit = [4/7 3/7] (M* #2 A((1/2 2/3)(0. 5 1/3)) #2 A((4/7)(3/7))) (4/7 3/7) (M* (expt-matrix #2 A((1/2 2/3)(0. 5 1/3)) 20) #2 A((1/9)(8/9))) #2 A((0. 571429)(0. 428572)) All probability vectors maps to the fixed vector (4/7, 3/7), the eigenvector of eigenvalue 1. (EIGENVALUES = (1 -1/6) 1/30/2022 rd 14

Ergodic Is matrix 0 0. 4 ergodic? Does it have a limit? 1 0. 6 Is it Regular? Does any power contain only positive values? (expt-matrix #2 A((0 0. 4)(1 0. 6)) 2) 0. 4 0. 24 0. 6 0. 76 Yes Find the limit by writing 0. 4 b = a; a + b = 1 (solve '((-1 2/5 0)(1 1 1))) (2/7 5/7) 1/30/2022 rd 15

Fixed Points and Regular Stochastic Matrices If matrix T is regular stochastic, then T has a unique fixed probability vector with positive components The sequence T, T 2, T 3 … approach a matrix whose columns are the fixed point. If p is any probability vector, the sequence of vectors Tp, T 2 p, T 3 p …approach the fixed point. The fixed point of imply b/2 = a or b = 2 a 2 a – 1 b = 0 1 a + 1 b = 1 (1/3 2/3) is fixed point 1/30/2022 rd 16

33. Markov Processes Example 1 Page 448 20% of the residents in region 1 move to region 2, and 10% move to region 3. Of the residents in region 2, 10% move to region 1 and 10% to region 3. In region 3, 20% move to region 1 and 10% to region 2. Find the probability that a resident in region 1 this year is a resident of region 1 next year; T 11 -- in 2 years. T 2 Given state vector a 0 = [0. 4 0. 3], find the distribution of the population 3 years from now. T 3 a 0. Find the steady state vector. #2 A((0. 3125)(0. 4375)(0. 25)) a 1 = Ta 0 … , an = Tna 0 From Region To 1 2 3 1 0. 7 0. 1 0. 2 2 0. 8 0. 1 3 0. 1 0. 7 (setf demo #2 A((0. 7 0. 1 0. 2)(0. 2 0. 8 0. 1)(0. 1 0. 7))) (M* demo) 0. 53 0. 17 0. 29 0. 31 0. 67 0. 19 0. 16 0. 52 (M* (expt-matrix demo 3) #2 A((0. 4)(0. 3))) #2 A((0. 3368)(0. 4024)(0. 2608) 1/30/2022 rd 17

Continued 34. Given T = ½ ¼ a/2 + b/4 = a or 2 a + b = 4 a; 2 a – b = 0 ½ ¾ 1 a + b = 1 find the probability of going from state 2 to state 1 after 2 steps (a 12)2 Find the steady state probabilities. (print-matrix (expt-matrix #2 A((1/2 1/4)(1/2 3/4)) 2)) 3/8 5/16 5/8 11/16 (expt-matrix #2 A((1/2 1/4)(1/2 3/4)) 30) 0. 33333 1/3 0. 66667 2/3 1/30/2022 rd 18

453 -31 Flu transition matrix flu no flu 0. 1 0. 2 for 200 dorm students no flu 0. 9 0. 8 120 students have the flu now, how many will have it 8 days from now? T 21 in 8 days? 12 days from now? Assume a 4 -day flu cycle Given 120 have the flu; 120/200 = ao = 3/5 2/5 T 2 a 0 (prn-mat (M* (expt-matrix #2 a((1/10 2/10)(9/10 8/10)) 2) #2 A((3/5)(2/5))) 93/500 407/500 => (* 200 93/500) 37. 2 will get the flu T 3 a 0 (prn-mat (M* (expt-matrix #2 a((1/10 2/10)(9/10 8/10)) 3) #2 A((3/5)(2/5))) #2 A((907/5000)(4093/5000)) (* 200 907/5000) 36. 28 will get the flu 1/30/2022 rd 19

Steady State Vector 35. Find the unique probability vector of the regular stochastic matrix. Start with a 0 = [a, b, 1 - a – b] => 0 0 ½ a 1 0 ½ b 0 1 -a-b ½ - a/2 – b/2 = a 3 a + b = 1 a + ½ - a/2 - b/2 = b a – 3 b = -1 b=1–a–b a + 2 b = 1 (solve '((3 1 1)(1 -3 -1)(1 2 1))) (1/5, 2/5) (Expt-Matrix #2 A((0 0 1/2)(1 0 1/2)(0 1 0)) 30) (0. 2 0. 4) 1/30/2022 rd 20

Flu Steady State Vector Find the steady state flu vector given transition matrix flu no flu 0. 1 0. 2 a 0. 1 a + 0. 2 b = a no flu 0. 9 0. 8 b 0. 9 a + 0. 8 b = b a+b=1 0. 9 a = 0. 2 b => 0. 9 a = 0. 2(1 – a) => a = 0. 2/1. 1 = 0. 1818 b = 0. 8191 (expt-matrix #2 a((0. 1 0. 2)(0. 9 0. 8)) 30) (0. 181818 0. 818181) 1/30/2022 rd 21

2 W 3 R a b a 1 W 1 R 1 W 2 R a b 2 R a 2 W 1 R b b c States: ai is number of red (state) in urn a In urn A are 2 White marbles and in urn B there are 3 Red marbles. At each step of the process a marble is randomly selected from each urn and switched. The states are a 0 = 0 red in urn a => state a 0 = [1 0 0] #2 A((0 1/6 0)(1 1/2 2/3)(0 1/3)) a b c a 0 1/6 0 Ex: b b: 1/2 * 1/3 + 1/2 * 2/3 = 1/2 b 1 1/2 2/3 b c: 1 * 1/3 c 0 1/3 (0. 1, 0. 6, 0. 3) final states Compute probability of 2 R marbles in Urn A after 3 steps and 2 in urn A after steady state (0. 3). a 2 = T 3 p 0 = (1/12 23/36 5/18); 0. 3 1/30/2022 rd 22

Other Notations Find given a 0 = (2/3, 0, 1/3) (prn-mat (expt-matrix #2 A((0 1/2 0)(1/2 1)(1/2 0 0)) 2)) 1/4 3/4 0 1/30/2022 1/4 1/2 1/2 0 rd 23

Absorbing Barriers A player has $2. He bets $1 at a time and wins with probability ½. He stops playing if he loses the $2 or wins $4. Compute probability that he will loose his money at the end of at most 5 plays. Find probability that the game will last more than 7 plays. p 0 = (0, 0, 1, 0 0) $2 State ai has i dollars. Player is the T matrix. a 0 a 1 a 2 a 3 a 4 a 5 a 6 a 0 1 ½ 0 0 0 a 1 0 0 ½ 0 0 a 2 0 ½ 0 0 0 a 3 0 0 ½ 0 0 a 4 0 0 0 ½ 0 a 5 0 0 ½ 0 0 a 6 0 0 0 ½ 1 Random walk with absorbing barriers at 0 (lose $2) and 6 (win $4). (M* (expt-matrix player 5) #2 A((0) (0)(1)(0)(0))) #2 A((3/8)(5/32)(0)(9/32)(0)(1/8)(1/16)) (M* (expt-matrix player 7) #2 A((0) (0)(1)(0)(0))) 2 A((29/64)(7/64)(0)(27/128)(0)(13/128)(1/8)) (sum (flatten '(7/64)(0)(27/128)(0)(13/128))) 27/64 1/30/2022 rd 24

Exercise 1 Given P = and the system is in state 2 [0 1] a) Find state vector X 2 , the probability of being in state 2 after 2 steps. (setf Y #2 A((0. 2 0. 6)(0. 8 0. 4))) IV #2 A((0)(1))) (M* Y IV) #2 A((0. 6)(0. 4)) (M* Y Y IV) #2 A((0. 36)(0. 64)) (M* Y #2 A((0. 6)(0. 4))) #2 A((0. 36)(0. 64)) b) Find (X 12)3 probability of going from state 2 to state 1 in 3 steps. (expt-matrix #2 A ((0. 2 0. 6)(0. 8 0. 4)) 3) #2 A((0. 392 0. 456)(0. 608 0. 544)) c) Find the equilibrium (steady state) vector (limit L). #2 A((0. 428572)(0. 571429)) d) Confirm using Px = x and solve where x = (a, b). 1/30/2022 rd 25

Exercise 2 Cars are classified as good fair or poor with transition matrix G F P Assume 100 cars are Good, 60 Fair and 20 Poor and weekly updated. Given a 0 = [5/9 3/9 1/9] a) How many cars will be found in each condition next week? (M* #2 A((0. 6 0. 2 0. 1)(0. 3 0. 6 0. 4)(0. 1 0. 2 0. 5)) #2 A((5/9)(3/9)(1/9))) #2 A((0. 411111)(0. 177778)) times 180 for weekly condition. b) Repeat for steady state conditions. #2 A((0. 293)(0. 463)(0. 244)) (mapcar #' * '(0. 293 0. 463 0. 244) '(180 180)) (52. 74 83. 34 43. 92) 1/30/2022 rd 26

Which to Lease? Two computer operating condition (OC) and not operating (NO) are given as O NO O 0. 95 0. 90 0. 98 0. 85 NO 0. 05 0. 10 0. 02 0. 15 Which one should be leased? (solve '((0. 05 -0. 90 0)(1 1 1))) (0. 947368 0. 052632) (solve '((0. 02 -0. 85 0)(1 1 1))) (0. 977012 0. 022989) 1/30/2022 rd 27

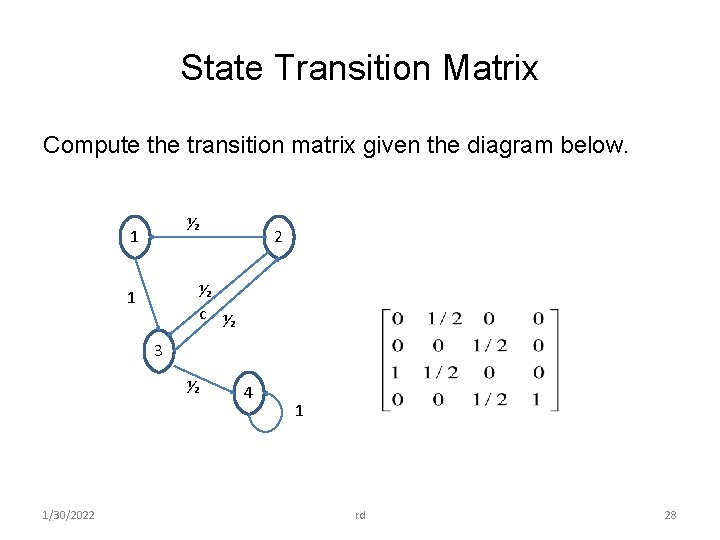
State Transition Matrix Compute the transition matrix given the diagram below. ½ 1 2 ½ c ½ 1 3 ½ 1/30/2022 4 1 rd 28

Absorbing States Once there, cannot exit. Bankrupt, home destroyed by fire, lake irreversibly polluted, Goal reached, game over, death 1/30/2022 rd 29

At a university, 60% of all first-semester students buy their books at the Campus Bookstore, and 40% buy their books at the Off-Campus Bookstore. See transition matrix below. If these trends continue, what percent of the market will each bookstore have at the beginning of the second semester? At the beginning of the third semester? The tenth semester? Recall: an = Tna 0 where T = 0. 9 0. 2 0. 1 0. 8 and a 0 = [0. 6 0. 4]. We found that a 1 = 0. 62 0. 38 a 2 = 0. 634 T= 0. 366 a 9 = 0. 6640 (solve '((-0. 1 0. 2 0)(1 1 1))) (2/3 1/3) 0. 3360 What is the distribution in later semesters? At some point, will the distribution stay the same from one semester to the next? Yes, because T is regular. 1/30/2022 rd‹#› 30

Students at an University Freshmen Dropouts Sophomores Graduated I Identity Matrix O Null Matrix A Absorbing N Non-absorbing D G F S 0. 1 0. 6 F 1 D D 1 0 0. 1 0. 05 G 0 1 0 0. 4 0. 3 0. 05 F 0 0 0. 6 0 S 0 0 0. 3 0. 55 S 0. 55 0. 4 1/30/2022 G 1 rd‹#› 31

Students at an University Abs Nabs 1 0 0. 6 0. 2 Identity Zero A Nabsorb Abs 0 1 0 0. 1 0. 2 NAbs 0 0 0. 3 0. 5 The fundamental matrix is F = (I – N)-1 time F S Conditional Prob = FA F S 1/30/2022 rd 32

Accounts Receivable Analysis Paid Bad Debt 0 -30 days 31 -90 days Paid 1 0 0 0 Bad Debt 0 1 0 0 0 -30 days 0. 4 0 0. 3 31 -90 days 0. 4 0. 2 0. 3 0. 1 Probability of 0 -30 days being paid is 89% and 11% bad debt. 31 -90, 74% being paid. 1/30/2022 rd 33

Application: 3 products A B C 0. 2 0. 1 0. 5 0. 2 0. 6 0. 4 0. 3 (expt-matrix #2 A((. 2. 1. 5)(. 2. 5. 2)(. 6. 4. 3)) 10) #2 A((0. 297 0. 286 0. 418) A + B = 29. 7 + 28. 6 = 58. 3 It costs $150 K to promote A only; 280 K to promote B only; Each percentage point is worth $10 K 0. 6 0. 4 0. 6 0. 1 0. 2 0. 3 0. 2 0. 4 0. 1 0. 5 0. 8 0. 5 0. 2 0. 3 0. 4 0. 0 0. 2 (expt-matrix #2 A((. 6. 4. 6)(. 2. 4. 1)(. 2. 2. 3)) 50) #2 A((0. 556 0. 222)) A + B = 77. 8, a 19. 5 * 10 K = $195 K 150 K => $45 K profit (expt-matrix #2 A((. 1. 2. 3)(. 5. 8. 5)(. 4 0. 2)) 50) #2 A((0. 190 0. 715 0. 095)) A + B = 0. 905 $322 K 280 K => $42 K 1/30/2022 rd 34

Markov From To A B C A 0. 85 0. 20 0. 15 B 0. 10 0. 75 0. 10 C 0. 05 0. 75 a) Compute steady state probabilities. (expt-matrix #2 A((0. 85 0. 20 0. 15)(0. 10 0. 75 0. 10)(0. 05 0. 75)) 20) #2 A((0. 547804 0. 547623 0. 547006)(0. 285663 0. 285844 0. 285663)(0. 166534 0. 167332)) b) Find market share for C. 0. 166534 1/30/2022 rd 35

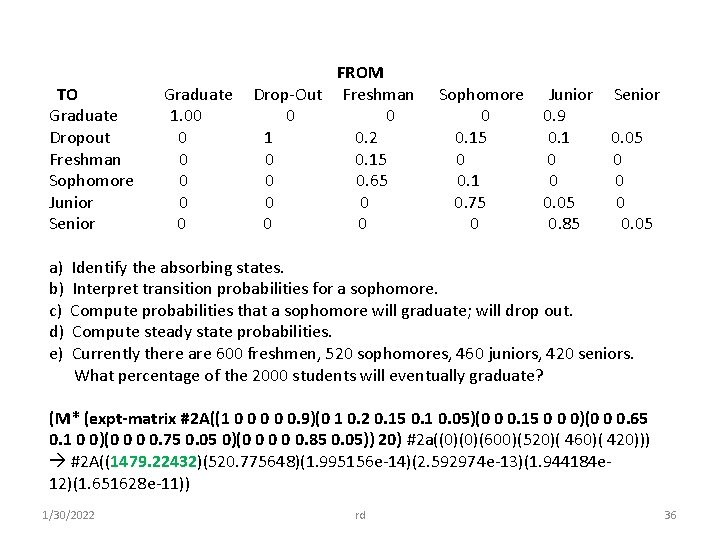
TO Graduate Dropout Freshman Sophomore Junior Senior a) b) c) d) e) Graduate 1. 00 0 0 FROM Drop-Out Freshman 0 0 1 0. 2 0 0. 15 0 0. 65 0 0 Sophomore 0 0. 15 0 0. 1 0. 75 0 Junior 0. 9 0. 1 0 0 0. 05 0. 85 Senior 0. 05 0 0. 05 Identify the absorbing states. Interpret transition probabilities for a sophomore. Compute probabilities that a sophomore will graduate; will drop out. Compute steady state probabilities. Currently there are 600 freshmen, 520 sophomores, 460 juniors, 420 seniors. What percentage of the 2000 students will eventually graduate? (M* (expt-matrix #2 A((1 0 0 0. 9)(0 1 0. 2 0. 15 0. 1 0. 05)(0 0 0. 15 0 0 0)(0 0 0. 65 0. 1 0 0)(0 0 0 0. 75 0. 05 0)(0 0 0. 85 0. 05)) 20) #2 a((0)(0)(600)(520)( 460)( 420))) #2 A((1479. 22432)(520. 775648)(1. 995156 e-14)(2. 592974 e-13)(1. 944184 e 12)(1. 651628 e-11)) 1/30/2022 rd 36

Pat walks along a four-blocks of an avenue. If at corner 1, 2, or 3, Pat walks to the left or right with probability ½. When at corner 4 or corner 0, Pat stays. 0 1 2 3 4 0 1 0 0 1 ½ 0 0 2 0 ½ 0 3 0 0 ½ 4 0 0 1 a) Find probabilities of ending in an absorbing state. b) On average, how long for the process to be absorbed? c) On average, how many times will the process be in each transient state? 1/30/2022 rd‹#› 37

States of an Ecosystem Find the states for the year given strontium 90 compartments a 0 = [20 60 15 20] 0. 85 0. 01 0 0 0. 05 0. 98 0. 2 0 0. 1 0 0. 8 0 0 0. 01 0 1 leaching 0. 05 Grasses Soil 0. 01 run-off growth 0. 01 Dead Organic matter 1/30/2022 Streams rd 38

Accounts receivable p b 1 2 p = paid; 1 = 1 -3 days overdue p 1 0. 5. 3 b = bad debt; 2 = 31 -60 days b 0 1 0. 3 I R absorbing 1 0 0. 3 0 O Q non absorbing 2 0 0. 2. 4 I – Q =. 7 0 (I – Q)-1 = F = #2 A((1. 429 0. 0)(0. 476 1. 667)) -. 2. 6 RF = (M* #2 A ((. 5. 3)(0. 3))#2 A((1. 429 0. 0)(0. 476 1. 667))) #2 A((0. 8573 0. 5001) If $10 K in 1 and $6 K in 2 then (0. 1428 0. 5001)) (M* #2 A((0. 8573 0. 5001)(0. 1428 0. 5001)) #2 a((10 e 3)(6 e 3))) #2 A((11573. 60)(4428. 60)) => (expected paid, expected bad debt) = $16 K ` 1/30/2022 rd 39