Optimality conditions for constrained local optima Lagrange multipliers

Optimality conditions for constrained local optima, Lagrange multipliers and their use for sensitivity of optimal solutions

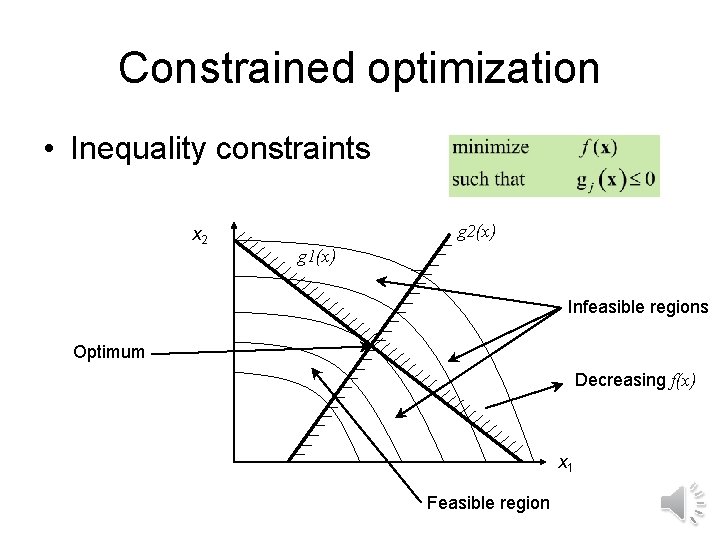
Constrained optimization • Inequality constraints x 2 g 2(x) g 1(x) Infeasible regions Optimum Decreasing f(x) x 1 Feasible region

Equality constraints • We will develop the optimality conditions for equality constraints and then generalize them for inequality constraints • Give an example of an engineering equality constraint.

Lagrangian and stationarity • Lagrangian function where j are unknown Lagrange multipliers • Stationary point conditions for equality constraints:

Example • Quadratic objective and constraint • Lagrangian • Stationarity conditions • Two stationary points

Inequality constraints • Inequality constraints require transformation to equality constraints: • This yields the following Lagrangian: • Why is the slack variable squared?

Karush-Kuhn-Tucker conditions • Conditions for stationary points are then: • If inequality constraint is inactive (t ≠ 0) then Lagrange multiplier = 0 • For minimum, non-negative multipliers

Convex problems • Convex optimization problem has – convex objective function – convex feasible domain if • All inequality constraints are convex (or gj = convex) • All equality constraints are linear – only one optimum • Karush-Kuhn-Tucker conditions necessary and will also be sufficient for global minimum • Why do the equality constraints have to be linear?

Example extended to inequality constraints • Minimize quadratic objective in a ring • Will use

Matlab’s fmincon function f=quad 2(x) f=x(1)^2+10*x(2)^2; function [c, ceq]=ring(x) global ri ro c(1)=ri^2 -x(1)^2 -x(2)^2; c(2)=x(1)^2+x(2)^2 -ro^2; ceq=[]; x 0=[1, 10]; ri=10. ; ro=20; [x, fval, exitflag, output, lambda]=fmincon(@quad 2, x 0, [], [], [], @ring)

Output message Warning: The default trust-region-reflective algorithm does not solve problems with the constraints you have specified. FMINCON will use the active-set algorithm instead. Local minimum found that satisfies the constraints. Optimization completed because the objective function is non-decreasing in feasible directions, to within the default value of the function tolerance, and constraints are satisfied to within the default value of the constraint tolerance. What assumption do you think Matlab makes in selec ting the default value of the constraint tolerance?

Solution x =10. 0000 -0. 0000 fval =100. 0000 lambda = lower: [2 x 1 double] upper: [2 x 1 double] eqlin: [0 x 1 double] eqnonlin: [0 x 1 double] ineqnonlin: [2 x 1 double] lambda. ineqnonlin’=1. 0000 0

Sensitivity of optimum solution to problem parameters Assuming problem fitness and constraints depend on parameter p The solution is and the corresponding fitness value

Sensitivity of optimum solution to problem parameters (contd. ) We would like to obtain derivatives of f* w. r. t. p After manipulating governing equations we obtain Lagrange multipliers called “shadow prices” because they provide the price of imposing constraints Why do we have ordinary derivative on the left side and partial on the right side?

Example • A simpler version of ring problem • For p=100 we found • Here it is easy to see that solution is • Which agrees with