Approximating functions polynomial interpolation Lagrange and Newtons divided









![Divided Difference Table x F[ ] F[ , , , ] x 0 F[x Divided Difference Table x F[ ] F[ , , , ] x 0 F[x](https://slidetodoc.com/presentation_image_h/f4d40ed03c4d7ea5881992ec336743a2/image-13.jpg)
![Divided Difference Table x F[ ] F[ , , ] 0 -5 2 -4 Divided Difference Table x F[ ] F[ , , ] 0 -5 2 -4](https://slidetodoc.com/presentation_image_h/f4d40ed03c4d7ea5881992ec336743a2/image-14.jpg)
![Divided Difference Table x F[ ] F[ , , ] 0 -5 2 -4 Divided Difference Table x F[ ] F[ , , ] 0 -5 2 -4](https://slidetodoc.com/presentation_image_h/f4d40ed03c4d7ea5881992ec336743a2/image-15.jpg)
![Divided Difference Table x F[ ] F[ , , ] 0 -5 2 -4 Divided Difference Table x F[ ] F[ , , ] 0 -5 2 -4](https://slidetodoc.com/presentation_image_h/f4d40ed03c4d7ea5881992ec336743a2/image-16.jpg)
![Divided Difference Table x F[ ] F[ , , ] 0 -5 2 -4 Divided Difference Table x F[ ] F[ , , ] 0 -5 2 -4](https://slidetodoc.com/presentation_image_h/f4d40ed03c4d7ea5881992ec336743a2/image-17.jpg)
![Divided Difference Table x F[ ] F[ , , ] 0 -5 2 -4 Divided Difference Table x F[ ] F[ , , ] 0 -5 2 -4](https://slidetodoc.com/presentation_image_h/f4d40ed03c4d7ea5881992ec336743a2/image-18.jpg)
![Divided Difference Table x F[ ] F[ , , ] 0 -5 2 -4 Divided Difference Table x F[ ] F[ , , ] 0 -5 2 -4](https://slidetodoc.com/presentation_image_h/f4d40ed03c4d7ea5881992ec336743a2/image-19.jpg)


![Example x 2 4 5 f(x) f[ , ] 3 1 5 -4 1 Example x 2 4 5 f(x) f[ , ] 3 1 5 -4 1](https://slidetodoc.com/presentation_image_h/f4d40ed03c4d7ea5881992ec336743a2/image-24.jpg)

















- Slides: 45

Approximating functions, polynomial interpolation (Lagrange and Newton’s divided differences) formulas, error approximations 1

Introduction to Interpolation p. Introduction p. Interpolation Problem p. Existence and Uniqueness p. Linear and Quadratic Interpolation p. Newton’s Divided Difference Method p. Properties of Divided Differences 2

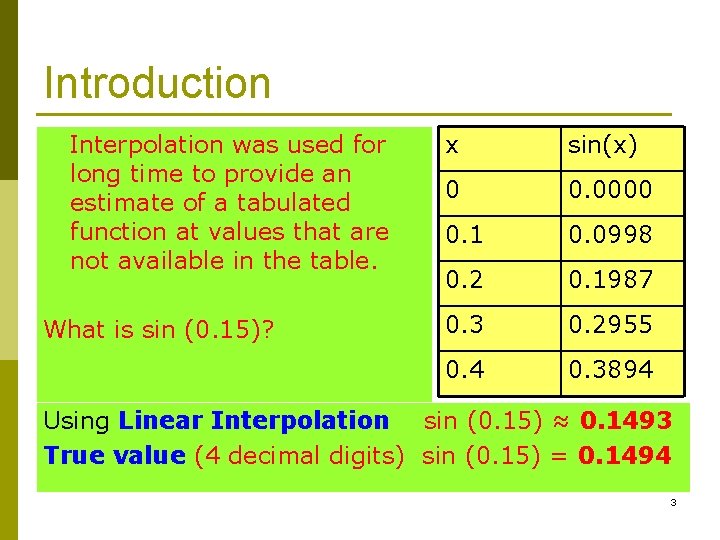
Introduction Interpolation was used for long time to provide an estimate of a tabulated function at values that are not available in the table. What is sin (0. 15)? x sin(x) 0 0. 0000 0. 1 0. 0998 0. 2 0. 1987 0. 3 0. 2955 0. 4 0. 3894 Using Linear Interpolation sin (0. 15) ≈ 0. 1493 True value (4 decimal digits) sin (0. 15) = 0. 1494 3

The Interpolation Problem Given a set of n+1 points, Find an nth order polynomial that passes through all points, such that: 4

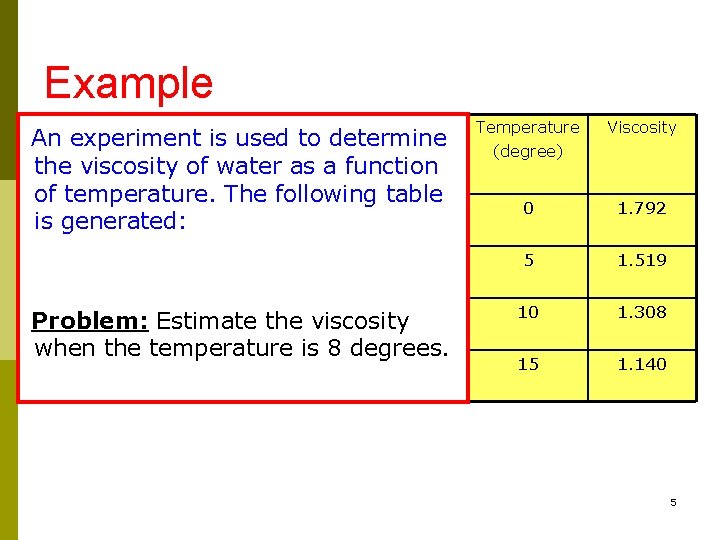
Example An experiment is used to determine the viscosity of water as a function of temperature. The following table is generated: Problem: Estimate the viscosity when the temperature is 8 degrees. Temperature (degree) Viscosity 0 1. 792 5 1. 519 10 1. 308 15 1. 140 5

Interpolation Problem Find a polynomial that fits the data points exactly. Linear Interpolation: V(T)= 1. 73 − 0. 0422 T V(8)= 1. 3924 6

Existence and Uniqueness Given a set of n+1 points: Assumption: are distinct Theorem: There is a unique polynomial fn(x) of order ≤ n such that: 7

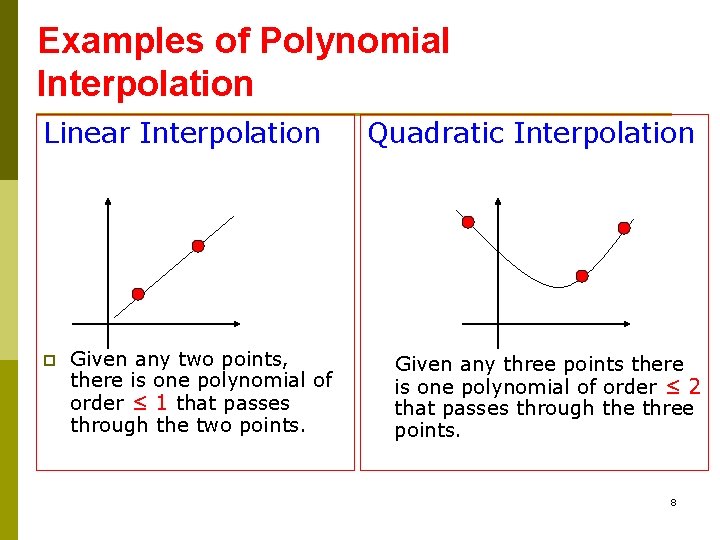
Examples of Polynomial Interpolation Linear Interpolation p Given any two points, there is one polynomial of order ≤ 1 that passes through the two points. Quadratic Interpolation Given any three points there is one polynomial of order ≤ 2 that passes through the three points. 8

Linear Interpolation Given any two points, The line that interpolates the two points is: Example : Find a polynomial that interpolates (1, 2) and (2, 4). 9

Quadratic Interpolation p Given any three points: p The polynomial that interpolates the three points is: 10

General nth Order Interpolation Given any n+1 points: The polynomial that interpolates all points is: 11

Divided Differences 12
![Divided Difference Table x F F x 0 Fx Divided Difference Table x F[ ] F[ , , , ] x 0 F[x](https://slidetodoc.com/presentation_image_h/f4d40ed03c4d7ea5881992ec336743a2/image-13.jpg)
Divided Difference Table x F[ ] F[ , , , ] x 0 F[x 0] F[x 0, x 1, x 2] F[x 0, x 1, x 2, x 3] x 1 F[x 1] F[x 1, x 2, x 3] x 2 F[x 2] F[x 2, x 3] x 3 F[x 3] 13
![Divided Difference Table x F F 0 5 2 4 Divided Difference Table x F[ ] F[ , , ] 0 -5 2 -4](https://slidetodoc.com/presentation_image_h/f4d40ed03c4d7ea5881992ec336743a2/image-14.jpg)
Divided Difference Table x F[ ] F[ , , ] 0 -5 2 -4 1 -3 6 -1 -15 Entries of the divided difference table are obtained from the data table using simple operations. f(xi) 0 -5 1 -3 -1 -15 14
![Divided Difference Table x F F 0 5 2 4 Divided Difference Table x F[ ] F[ , , ] 0 -5 2 -4](https://slidetodoc.com/presentation_image_h/f4d40ed03c4d7ea5881992ec336743a2/image-15.jpg)
Divided Difference Table x F[ ] F[ , , ] 0 -5 2 -4 1 -3 6 -1 -15 f(xi) 0 1 -1 -5 -3 -15 The first two column of the table are the data columns. Third column: First order differences. Fourth column: Second order differences. 15
![Divided Difference Table x F F 0 5 2 4 Divided Difference Table x F[ ] F[ , , ] 0 -5 2 -4](https://slidetodoc.com/presentation_image_h/f4d40ed03c4d7ea5881992ec336743a2/image-16.jpg)
Divided Difference Table x F[ ] F[ , , ] 0 -5 2 -4 1 -3 6 -1 -15 0 -5 1 -3 -1 -15 16
![Divided Difference Table x F F 0 5 2 4 Divided Difference Table x F[ ] F[ , , ] 0 -5 2 -4](https://slidetodoc.com/presentation_image_h/f4d40ed03c4d7ea5881992ec336743a2/image-17.jpg)
Divided Difference Table x F[ ] F[ , , ] 0 -5 2 -4 1 -3 6 -1 -15 0 -5 1 -3 -1 -15 17
![Divided Difference Table x F F 0 5 2 4 Divided Difference Table x F[ ] F[ , , ] 0 -5 2 -4](https://slidetodoc.com/presentation_image_h/f4d40ed03c4d7ea5881992ec336743a2/image-18.jpg)
Divided Difference Table x F[ ] F[ , , ] 0 -5 2 -4 1 -3 6 -1 -15 0 -5 1 -3 -1 -15 18
![Divided Difference Table x F F 0 5 2 4 Divided Difference Table x F[ ] F[ , , ] 0 -5 2 -4](https://slidetodoc.com/presentation_image_h/f4d40ed03c4d7ea5881992ec336743a2/image-19.jpg)
Divided Difference Table x F[ ] F[ , , ] 0 -5 2 -4 1 -3 6 -1 -15 0 -5 1 -3 -1 -15 f 2(x)= F[x 0]+F[x 0, x 1] (x-x 0)+F[x 0, x 1, x 2] (x-x 0)(x-x 1) 19

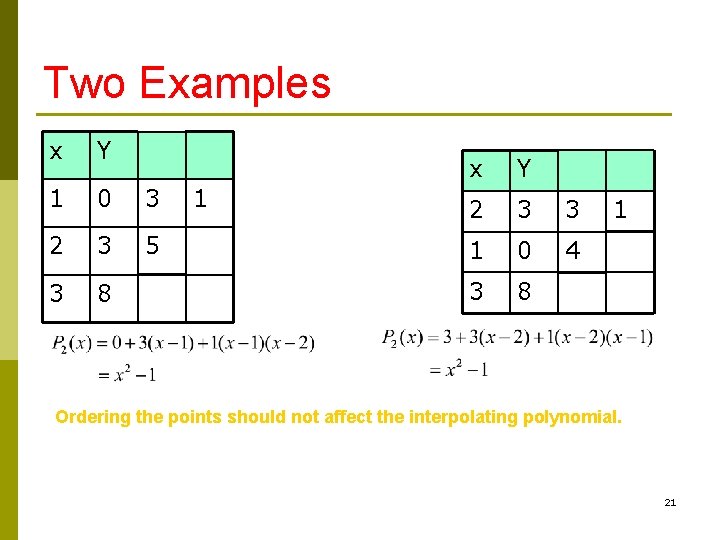
Two Examples Obtain the interpolating polynomials for the two examples: x y 1 0 2 3 1 0 3 8 What do you observe? 20

Two Examples x Y 1 0 3 2 3 5 3 8 1 x Y 2 3 3 1 0 4 3 8 1 Ordering the points should not affect the interpolating polynomial. 21

Properties of Divided Difference Ordering the points should not affect the divided difference: 22

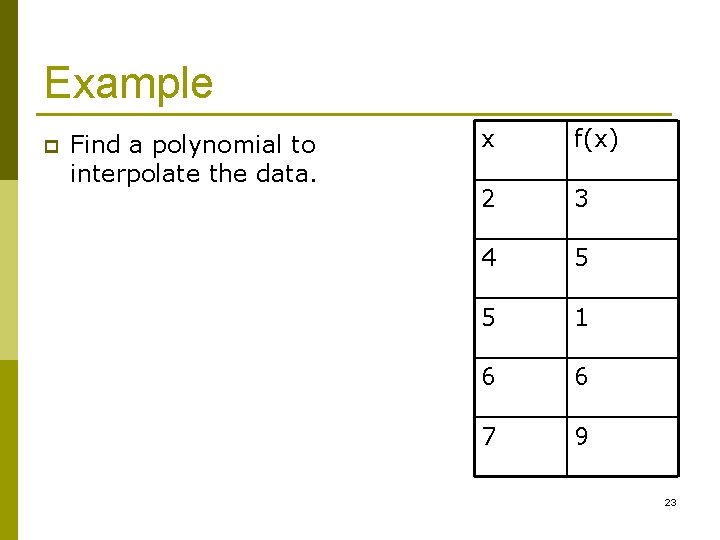
Example p Find a polynomial to interpolate the data. x f(x) 2 3 4 5 5 1 6 6 7 9 23
![Example x 2 4 5 fx f 3 1 5 4 1 Example x 2 4 5 f(x) f[ , ] 3 1 5 -4 1](https://slidetodoc.com/presentation_image_h/f4d40ed03c4d7ea5881992ec336743a2/image-24.jpg)
Example x 2 4 5 f(x) f[ , ] 3 1 5 -4 1 5 6 7 6 9 f[ , , ] -1. 6667 4. 5 -1 f[ , , , ] 1. 5417 -1. 8333 f[ , , ] -0. 6750 3 24

Summary 25

Lagrange Interpolation 26

The Interpolation Problem Given a set of n+1 points: Find an nth order polynomial: that passes through all points, such that: 27

Lagrange Interpolation Problem: Given Find the polynomial of least order …. …. such that: Lagrange Interpolation Formula: 28

Lagrange Interpolation 29

Lagrange Interpolation Example x y 1/3 1/4 1 2 -1 7 30

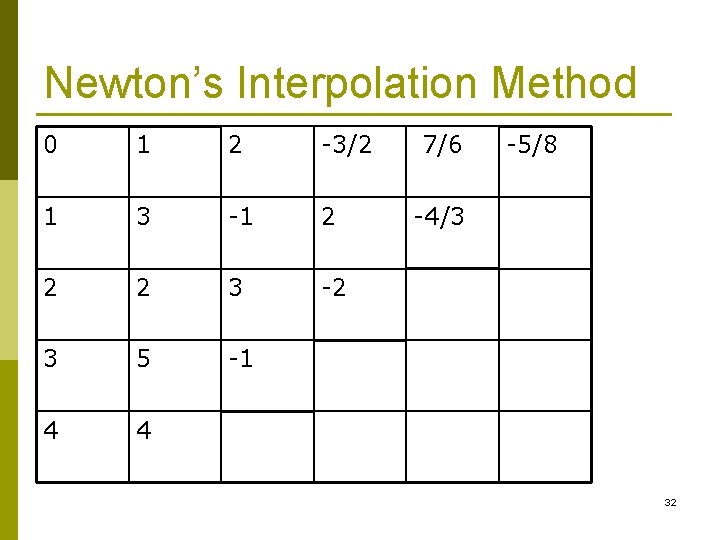
Example Find a polynomial to interpolate: x y 0 1 Both Newton’s interpolation method and Lagrange 1 interpolation method must give the same answer. 2 3 5 4 4 31

Newton’s Interpolation Method 0 1 2 -3/2 1 3 -1 2 2 2 3 -2 3 5 -1 4 4 7/6 -5/8 -4/3 32

Interpolating Polynomial 33

Interpolating Polynomial Using Lagrange Interpolation Method 34

Inverse Interpolation Error in Polynomial Interpolation 35

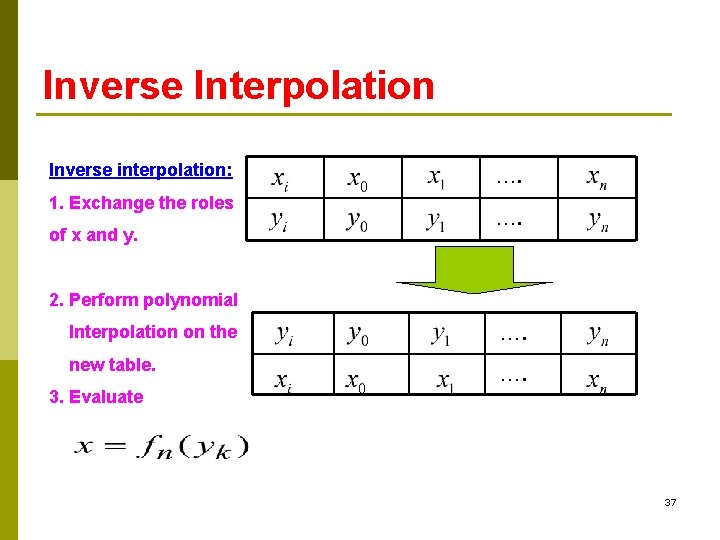
Inverse Interpolation …. …. One approach: Use polynomial interpolation to obtain fn(x) to interpolate the data then use Newton’s method to find a solution to x 36

Inverse Interpolation Inverse interpolation: …. 1. Exchange the roles …. of x and y. 2. Perform polynomial Interpolation on the …. new table. …. 3. Evaluate 37

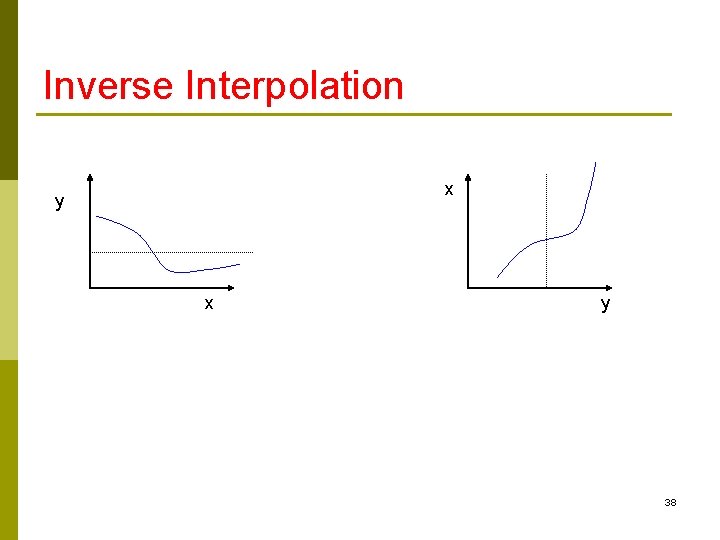
Inverse Interpolation x y 38

Inverse Interpolation Question: What is the limitation of inverse interpolation? • The original function has an inverse. • y 1, y 2, …, yn must be distinct. 39

Inverse Interpolation Example x y 3. 2 1 -. 8333 2. 0 2 -2. 5 1. 6 3 1 2 3 3. 2 2. 0 1. 6 1. 0417 40

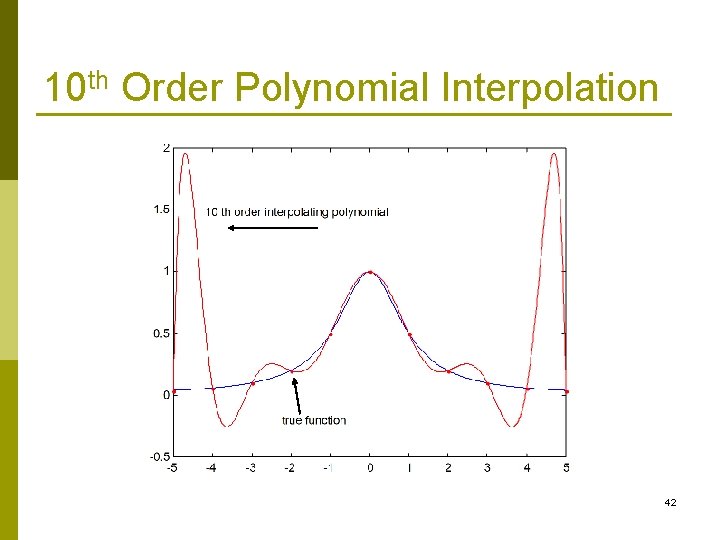
Errors in polynomial Interpolation p Polynomial interpolation may lead to large errors (especially for high order polynomials). BE CAREFUL p When an nth order interpolating polynomial is used, the error is related to the (n+1)th order derivative. 41

10 th Order Polynomial Interpolation 42

Errors in polynomial Interpolation Theorem 43

Example 44

Summary The interpolating polynomial is unique. p Different methods can be used to obtain it. p n n n Newton’s divided difference Lagrange interpolation Others Polynomial interpolation can be sensitive to data. p BE CAREFUL when high order polynomials are used. p 45
 Spline interpolation vs polynomial interpolation
Spline interpolation vs polynomial interpolation Lagrange interpolation formula
Lagrange interpolation formula Interpolation
Interpolation Lagrange
Lagrange Secret sharing lagrange interpolation
Secret sharing lagrange interpolation Divided difference interpolation
Divided difference interpolation Newton's forward difference formula
Newton's forward difference formula Estimating square roots to the nearest hundredth
Estimating square roots to the nearest hundredth Approximating calculations
Approximating calculations Neville polynomial interpolation
Neville polynomial interpolation Polynomial interpolation
Polynomial interpolation Lagrange basis functions
Lagrange basis functions Numpy.polynomial.polynomial
Numpy.polynomial.polynomial How to divide a polynomial by another polynomial
How to divide a polynomial by another polynomial Polynomial standard form
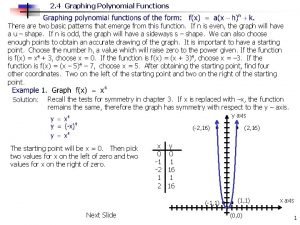
Polynomial standard form Chapter 4 polynomial and rational functions
Chapter 4 polynomial and rational functions Chapter 3 polynomial and rational functions
Chapter 3 polynomial and rational functions Factoring patterns
Factoring patterns Polynomial review
Polynomial review Linear polynomial
Linear polynomial Evaluate and graph polynomial functions
Evaluate and graph polynomial functions Polynomial functions and their graphs
Polynomial functions and their graphs Analyzing graphs of polynomial functions calculator
Analyzing graphs of polynomial functions calculator Chapter 3 polynomial and rational functions
Chapter 3 polynomial and rational functions Lagrange, euler, and kovalevskaya tops
Lagrange, euler, and kovalevskaya tops What is an abelian group
What is an abelian group Lagrange's theorem formula
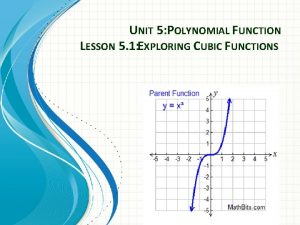
Lagrange's theorem formula Algebra 2 unit 5 polynomial functions
Algebra 2 unit 5 polynomial functions Structure in graphs of polynomial functions
Structure in graphs of polynomial functions 5-1 polynomial functions
5-1 polynomial functions What is a leading term in polynomials
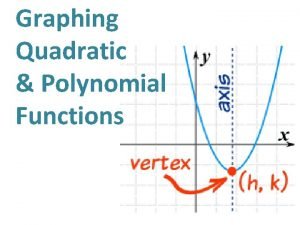
What is a leading term in polynomials Graphing polynomial functions
Graphing polynomial functions Investigating graphs of polynomial functions
Investigating graphs of polynomial functions Investigating graphs of polynomial functions
Investigating graphs of polynomial functions End behaviour chart
End behaviour chart Rational equations
Rational equations Direct substitution polynomial
Direct substitution polynomial Algebra 2 polynomial functions
Algebra 2 polynomial functions How do you evaluate polynomial functions
How do you evaluate polynomial functions Transforming polynomial functions quiz part one
Transforming polynomial functions quiz part one Polynomial function practice
Polynomial function practice Odd degree polynomial
Odd degree polynomial Transformations polynomial functions
Transformations polynomial functions Polynomial function examples
Polynomial function examples Finding degree and leading coefficient
Finding degree and leading coefficient Closure property of polynomials
Closure property of polynomials