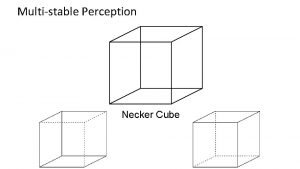
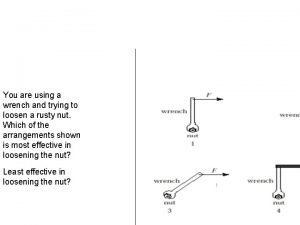
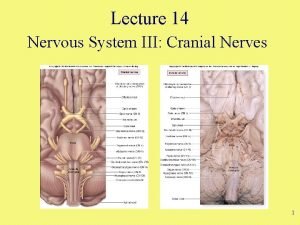
Groningen June 3 2009 1 From Spinning Tops

Groningen, June 3, 2009 1

From Spinning Tops to Rigid Body Motion 2 S 3 Peter H. Richter University of Bremen S 3 S 1 x. S 2 Department of Mathematics, University of Groningen, June 3, 2009 2

Outline • • • Demonstration of some basic physics Parameter sets Configuration spaces SO(3) and S 2 vs. T 3 and T 2 Phase space structure Equations of motion Strategies of investigation Groningen, June 3, 2009 3

• • • Demonstration of some basic physics Parameter sets Configuration spaces SO(3) and S 2 vs. T 3 and T 2 Phase space structure Equations of motion Strategies of investigation Groningen, June 3, 2009 4

Parameter space 6 essential parameters after scaling of lengths, time, energy: two moments of inertia a, b (g = 1 -a-b) at least one independent moment of inertia r for the Cardan frame two angles s, t for the center of gravity angle d between the frame‘s axis and the direction of gravity Groningen, June 3, 2009 5

• • • Demonstration of some basic physics Parameter sets Configuration spaces SO(3) and S 2 vs. T 3 and T 2 Phase space structure Equations of motion Strategies of investigation Groningen, June 3, 2009 6

Configuration spaces SO(3) versus T 3 (j, q, y) Euler angles (j, q, y) (j + p, 2 p - q, y + p) Cardan angles (j, q, y) after separation of angle j: reduced configuration spaces Poisson (q, y)-sphere Poisson (q, y)-torus „polar points“ q = 0, p defined with respect to an arbitrary direction „polar y-circles“ q = 0, p defined with respect to the axes of the frame coordinate singularities removed, but Euler variables lost Groningen, June 3, 2009 7

• • • Demonstration of some basic physics Parameter sets Configuration spaces SO(3) and S 2 vs. T 3 and T 2 Phase space structure Equations of motion Strategies of investigation Groningen, June 3, 2009 8

Phase space and conserved quantities 3 angles + 3 momenta 6 D phase space energy conservation h = const 5 D energy surfaces strong chaos one angular momentum lz = const 4 D invariant sets mild chaos 3 conserved quantities 3 D invariant sets integrable 4 conserved quantities 2 D invariant sets super-integrable Groningen, June 3, 2009 9

Reduced phase spaces with parameter lz 2 angles + 2 momenta 4 D phase space energy conservation h = const 3 D energy surfaces 2 conserved quantities 2 D invariant sets 3 conserved quantities 1 D invariant sets Groningen, June 3, 2009 chaos integrable super-integrable 10

( g, l ) - phase space 3 gi -components + 3 momenta li 6 D phase space 2 Casimir constants g ·g = 1 and g ·l = lz 4 D simplectic space energy conservation h = const 3 D energy surfaces chaos 2 conserved quantities 2 D invariant sets integrable 3 conserved quantities 1 D invariant sets super-integrable Groningen, June 3, 2009 11

• • • Demonstration of some basic physics Parameter sets Configuration spaces SO(3) and S 2 vs. T 3 and T 2 Phase space structure Equations of motion Strategies of investigation Groningen, June 3, 2009 12

Without frame: Euler-Poisson equations in (g, l)-space Coordinates: j motion: Casimir constants: Energy constant: Effective potential: Groningen, June 3, 2009 13

With frame: Euler – Lagrange equations Demo where Reduction to a Hamiltonian Coriolisforce and centrifugal potential Groningen, June 3, 2009 with parameter , 14

• • • Demonstration of some basic physics Parameter sets Configuration spaces SO(3) and S 2 vs. T 3 and T 2 Phase space structure Equations of motion Strategies of investigation Groningen, June 3, 2009 15

Search for invariant sets in phase space, and their bifurcations • • • topological bifurcations of iso-energy surfaces their projections to configuration and momentum spaces integrable systems: action variable representation and foliation by invariant tori chaotic systems: Poincaré sections periodic orbit skeleton: stable (order) and unstable (chaos) Groningen, June 3, 2009 Katok Envelope Actions Tori Poincaré Periods 16

Groningen, June 3, 2009 17

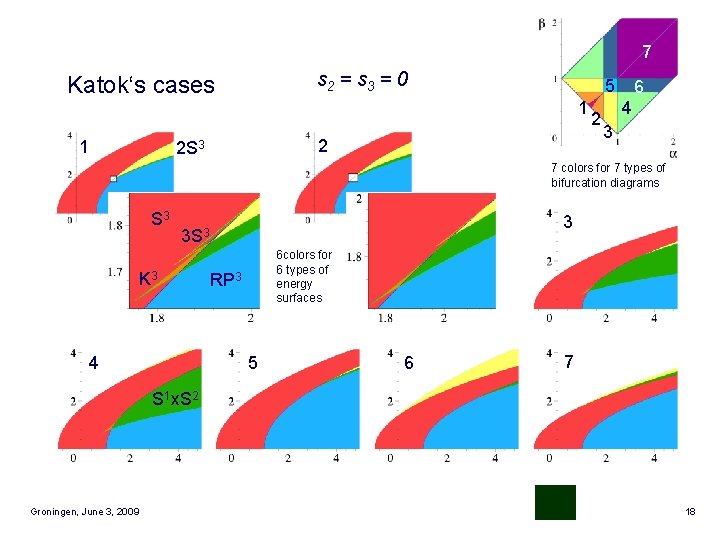
7 s 2 = s 3 = 0 Katok‘s cases 1 5 6 4 1 2 3 2 2 S 3 7 colors for 7 types of bifurcation diagrams S 3 3 3 S 3 K 3 4 6 colors for 6 types of energy surfaces RP 3 5 6 7 S 1 x. S 2 Groningen, June 3, 2009 18

7+1 types of envelopes (I) S 3 I T 2 (h, l) = (1, 1) Groningen, June 3, 2009 S 3 I‘ (A 1, A 2, A 3) = (1. 7, 0. 9, 0. 86) T 2 (1, 0. 6) 2 S 3 II 2 T 2 (2. 5, 2. 15) S 1 x. S 2 III M 3 2 (2, 1. 8) 19

7+1 types of envelopes (II) RP 3 IV T 2 (1. 5, 0. 6) Groningen, June 3, 2009 K 3 V (A 1, A 2, A 3) = (1. 7, 0. 9, 0. 86) M 3 2 (1. 85, 1. 705) 3 S 3 VI 2 S 2, T 2 (1. 9, 1. 759) S 3, S 1 x. S 2 VII 2 T 2 (1. 912, 1. 763) 20

Energy surfaces in action representation Euler Groningen, June 3, 2009 Lagrange Kovalevskaya 21

Groningen, June 3, 2009 22

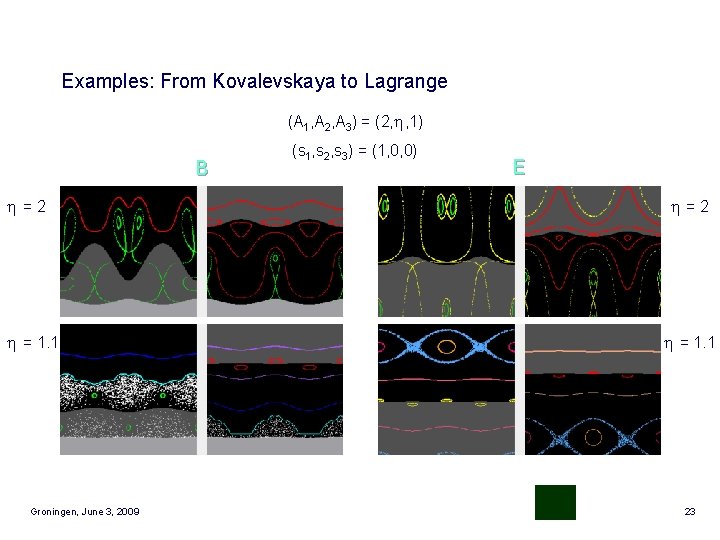
Examples: From Kovalevskaya to Lagrange (A 1, A 2, A 3) = (2, , 1) B =2 = 1. 1 Groningen, June 3, 2009 (s 1, s 2, s 3) = (1, 0, 0) E =2 = 1. 1 23

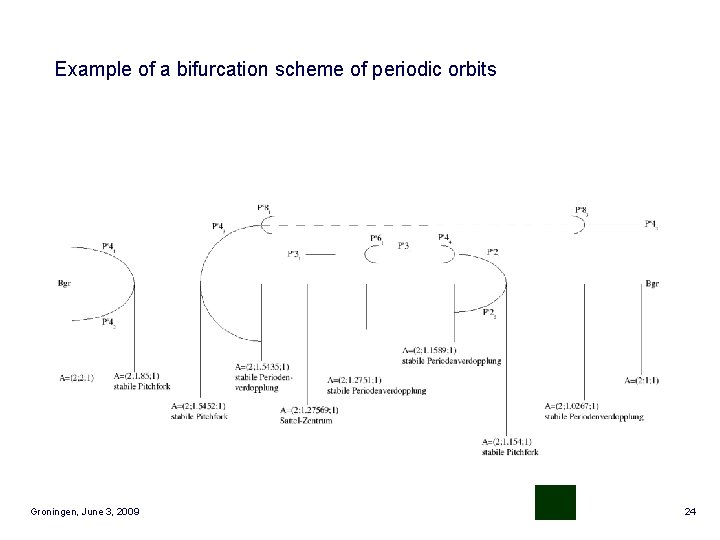
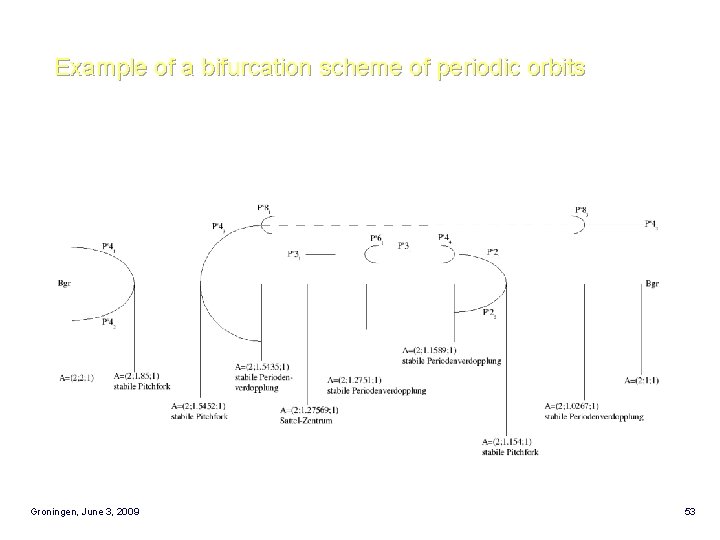
Example of a bifurcation scheme of periodic orbits Groningen, June 3, 2009 24

Groningen, June 3, 2009 25

Lagrange tops without frame Three types of bifurcation diagrams: 0. 5 < a < 0. 75 (discs), 0. 75 < a < 1 (balls), a > 1 (cigars) five types of Reeb graphs When the 3 -axis is the symmetry axis, the system remains integrable with the frame, otherwise not. VB Lagrange Groningen, June 3, 2009 26

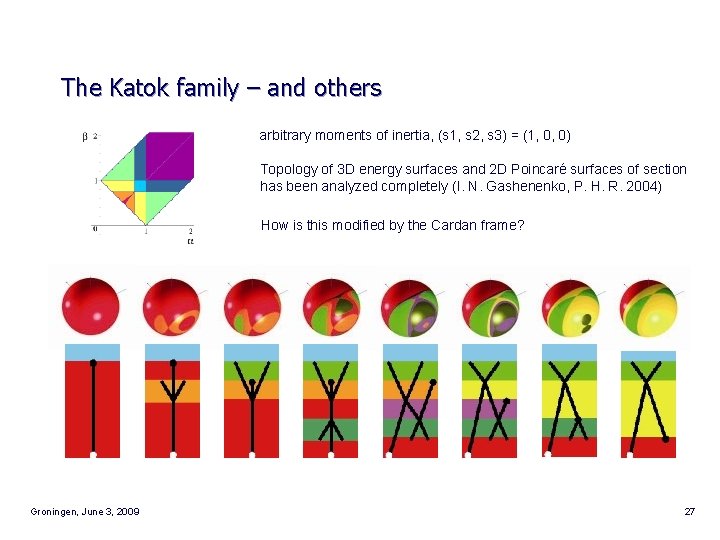
The Katok family – and others arbitrary moments of inertia, (s 1, s 2, s 3) = (1, 0, 0) Topology of 3 D energy surfaces and 2 D Poincaré surfaces of section has been analyzed completely (I. N. Gashenenko, P. H. R. 2004) How is this modified by the Cardan frame? Groningen, June 3, 2009 27

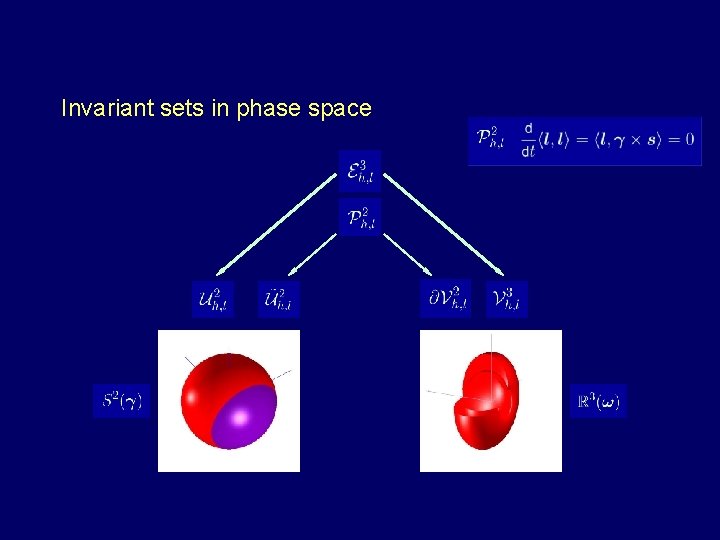
Invariant sets in phase space Groningen, June 3, 2009 28

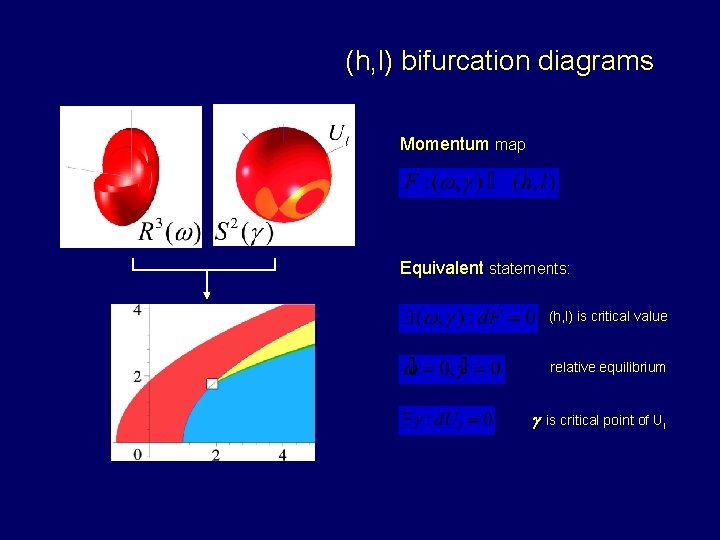
(h, l) bifurcation diagrams Momentum map Equivalent statements: (h, l) is critical value relative equilibrium g is critical point of Ul Groningen, June 3, 2009 29

Rigid body dynamics in SO(3) - - Phase spaces and basic equations • Full and reduced phase spaces • Euler-Poisson equations • Invariant sets and their bifurcations Integrable cases • • • - Katok‘s more general cases • • • - Effective potentials Bifurcation diagrams Enveloping surfaces Poincaré surfaces of section • • • Groningen, June 3, 2009 Euler Lagrange Kovalevskaya Gashenenko‘s version Dullin-Schmidt version An application 30

Integrable cases A Euler: „gravity-free“ E Lagrange: „heavy“, symmetric L Kovalevskaya: K Groningen, June 3, 2009 31

Euler‘s case Poisson sphere potential (h, l)-bifurcation diagram l-motion decouples from g-motion admissible values in (p, q, r)-space for given l and h < Ul B Groningen, June 3, 2009 32

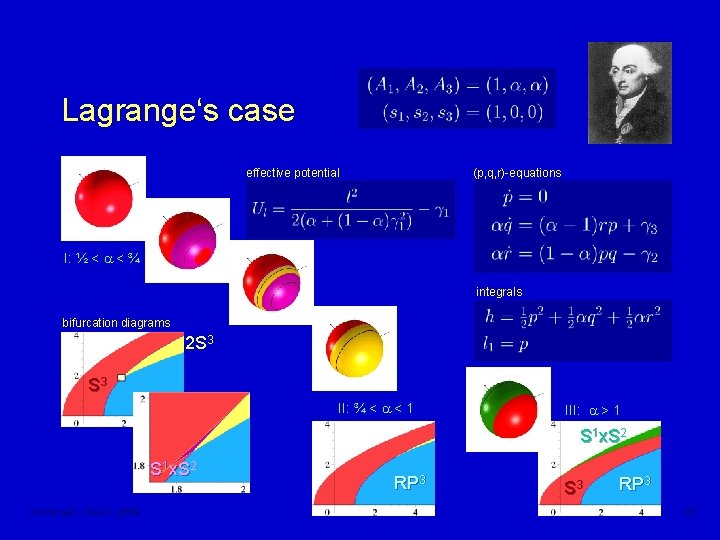
Lagrange‘s case effective potential (p, q, r)-equations I: ½ < a < ¾ integrals bifurcation diagrams 2 S 3 II: ¾ < a < 1 III: a > 1 S 1 x. S 2 Groningen, June 3, 2009 RP 3 S 3 RP 3 33

Enveloping surfaces B Groningen, June 3, 2009 34

Kovalevskaya‘s case Tori projected to (p, q, r)-space Tori in phase space and Poincaré surface of section (p, q, r)-equations integrals Groningen, June 3, 2009 35

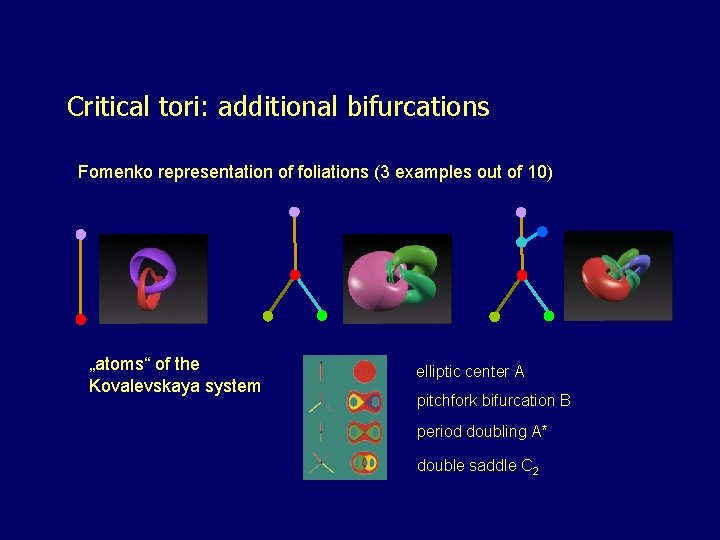
Critical tori: additional bifurcations Fomenko representation of foliations (3 examples out of 10) „atoms“ of the Kovalevskaya system elliptic center A pitchfork bifurcation B period doubling A* double saddle C 2 Groningen, June 3, 2009 36

Energy surfaces in action representation Euler Groningen, June 3, 2009 Lagrange Kovalevskaya 37

Rigid body dynamics in SO(3) - - Phase spaces and basic equations • Full and reduced phase spaces • Euler-Poisson equations • Invariant sets and their bifurcations Integrable cases • • • - Katok‘s more general cases • • • - Effective potentials Bifurcation diagrams Enveloping surfaces Poincaré surfaces of section • • • Groningen, June 3, 2009 Euler Lagrange Kovalevskaya Gashenenko‘s version Dullin-Schmidt version An application 38

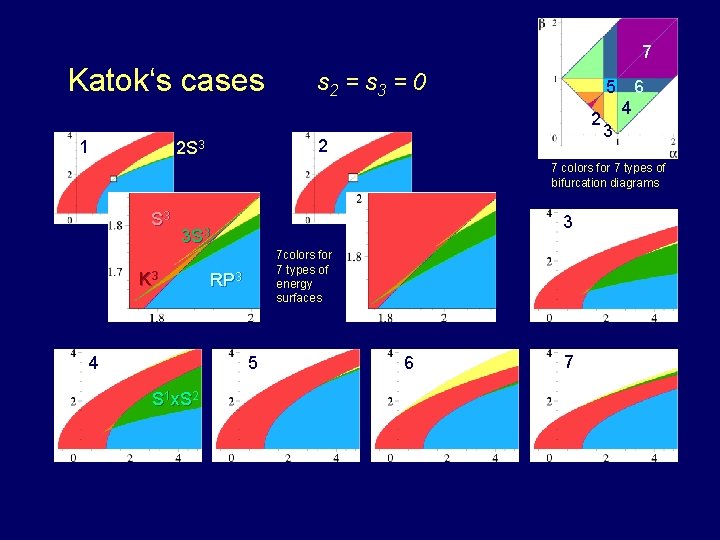
7 Katok‘s cases 1 s 2 = s 3 = 0 5 6 1 4 2 3 2 2 S 3 7 colors for 7 types of bifurcation diagrams S 3 3 3 S 3 K 3 4 7 colors for 7 types of energy surfaces RP 3 5 6 7 S 1 x. S 2 Groningen, June 3, 2009 39

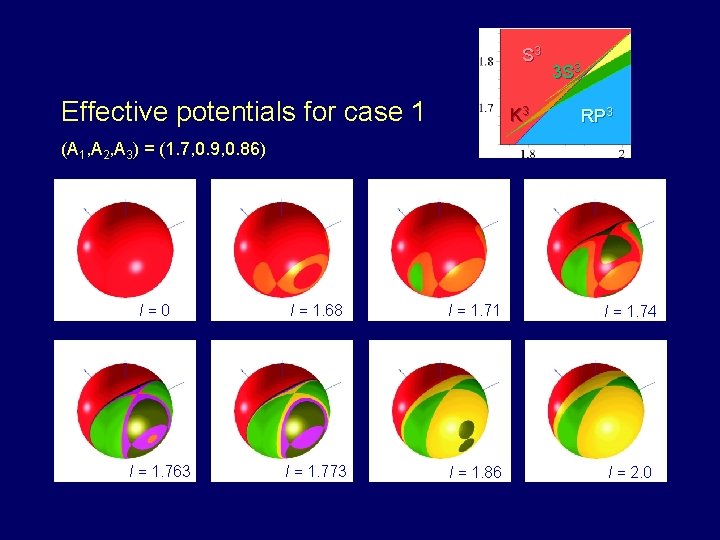
S 3 Effective potentials for case 1 K 3 3 S 3 RP 3 (A 1, A 2, A 3) = (1. 7, 0. 9, 0. 86) l=0 l = 1. 763 Groningen, June 3, 2009 l = 1. 68 l = 1. 71 l = 1. 74 l = 1. 773 l = 1. 86 l = 2. 0 40

7+1 types of envelopes (I) S 3 I T 2 (h, l) = (1, 1) Groningen, June 3, 2009 S 3 I‘ T 2 (1, 0. 6) 2 S 3 II (A 1, A 2, A 3) = (1. 7, 0. 9, 0. 86) 2 T 2 (2. 5, 2. 15) S 1 x. S 2 III M 3 2 (2, 1. 8) 41

7+1 types of envelopes (II) RP 3 IV T 2 (1. 5, 0. 6) Groningen, June 3, 2009 K 3 V M 3 2 (1. 85, 1. 705) 3 S 3 VI (A 1, A 2, A 3) = (1. 7, 0. 9, 0. 86) 2 S 2, T 2 (1. 9, 1. 759) S 3, S 1 x. S 2 VII 2 T 2 (1. 912, 1. 763) 42

2 variations of types II and III A = (0. 8, 1. 1, 0. 9) 2 S 3 2 S 2 A = (0. 8, 1. 1, 1. 0) S 1 x. S 2 T 2 Only in cases II‘ and III‘ are the envelopes free of singularities. Case II‘ occurs in Katok‘s regions 4, 6, 7, case III‘ only in region 7. II‘ (3. 6, 2. 8) III‘ (3. 6, 2. 75) This completes the list of all possible types of envelopes in the Katok case. There are more in the more general cases where only s 3=0 (Gashenenko) or none of the si = 0 (not done yet). Groningen, June 3, 2009 43

Rigid body dynamics in SO(3) - - Phase spaces and basic equations • Full and reduced phase spaces • Euler-Poisson equations • Invariant sets and their bifurcations Integrable cases • • • - Katok‘s more general cases • • • - Effective potentials Bifurcation diagrams Enveloping surfaces Poincaré surfaces of section • • • Groningen, June 3, 2009 Euler Lagrange Kovalevskaya Gashenenko‘s version Dullin-Schmidt version An application 44

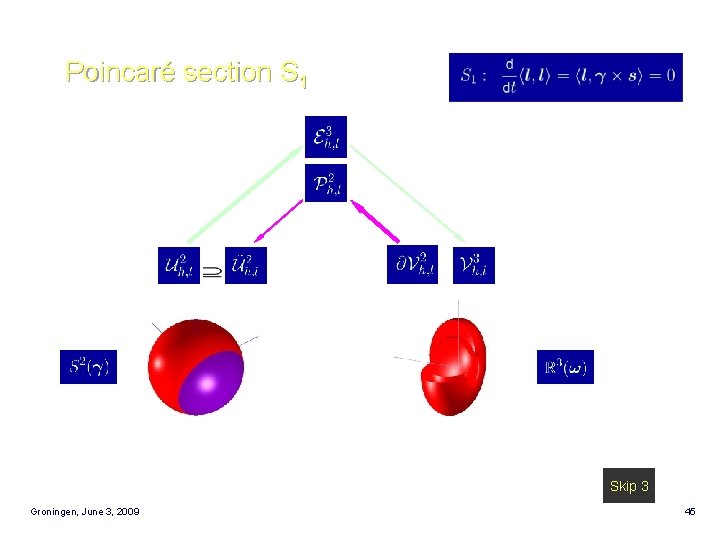
Poincaré section S 1 Skip 3 Groningen, June 3, 2009 45

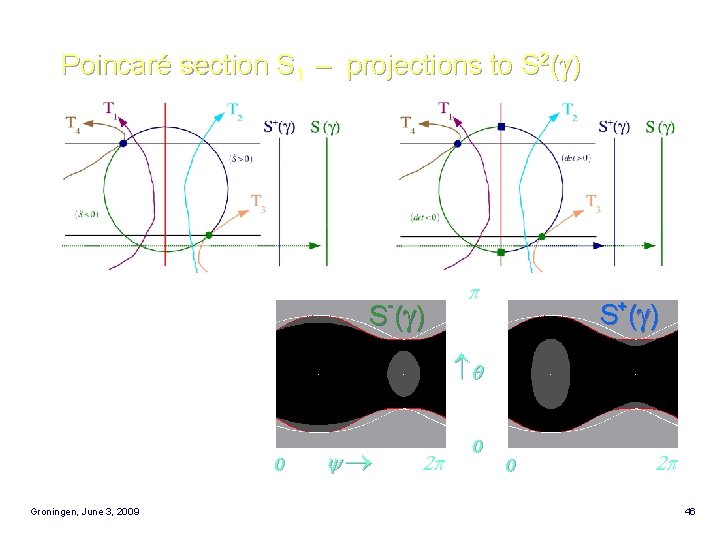
Poincaré section S 1 – projections to S 2(g) S (g ) - p S + (g ) q 0 Groningen, June 3, 2009 2 p 0 0 2 p 46

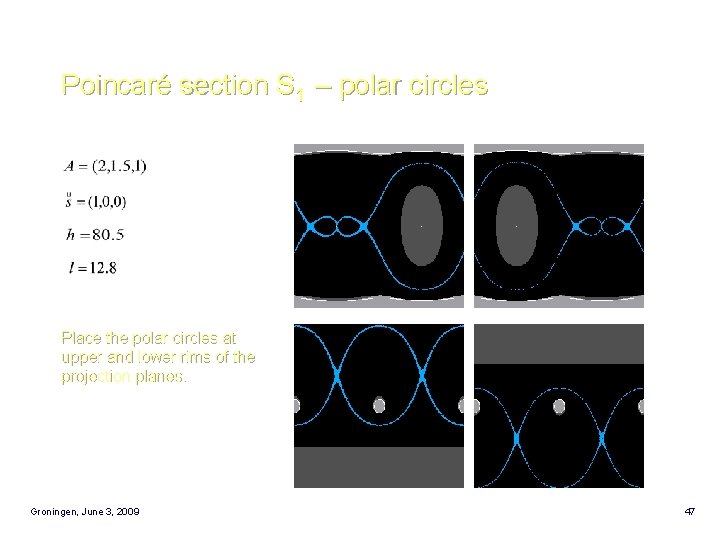
Poincaré section S 1 – polar circles Place the polar circles at upper and lower rims of the projection planes. Groningen, June 3, 2009 47

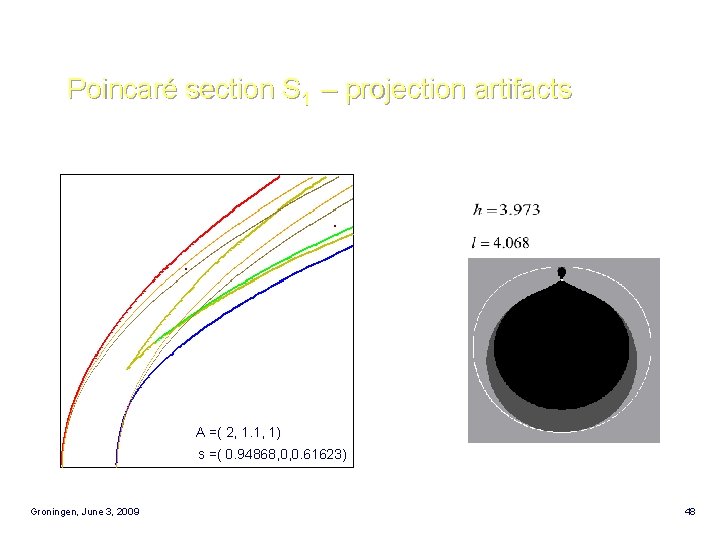
Poincaré section S 1 – projection artifacts A =( 2, 1. 1, 1) s =( 0. 94868, 0, 0. 61623) Groningen, June 3, 2009 48

Explicit formulae for the two sections with S 1: S 2: where Groningen, June 3, 2009 49

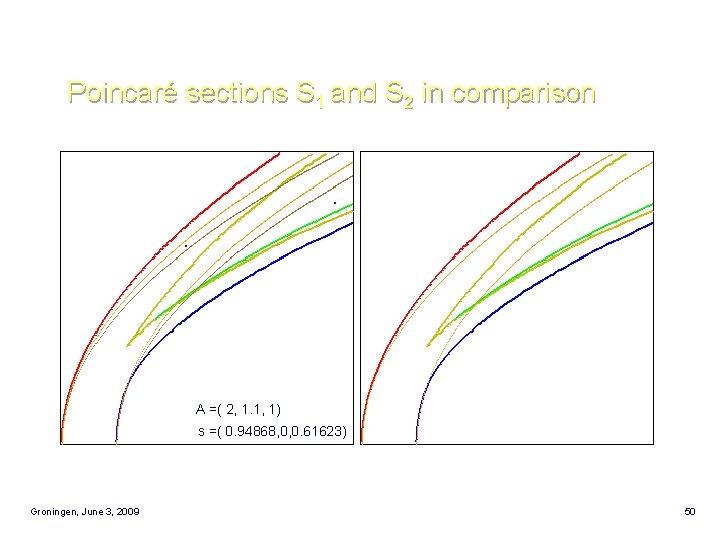
Poincaré sections S 1 and S 2 in comparison A =( 2, 1. 1, 1) s =( 0. 94868, 0, 0. 61623) Groningen, June 3, 2009 50

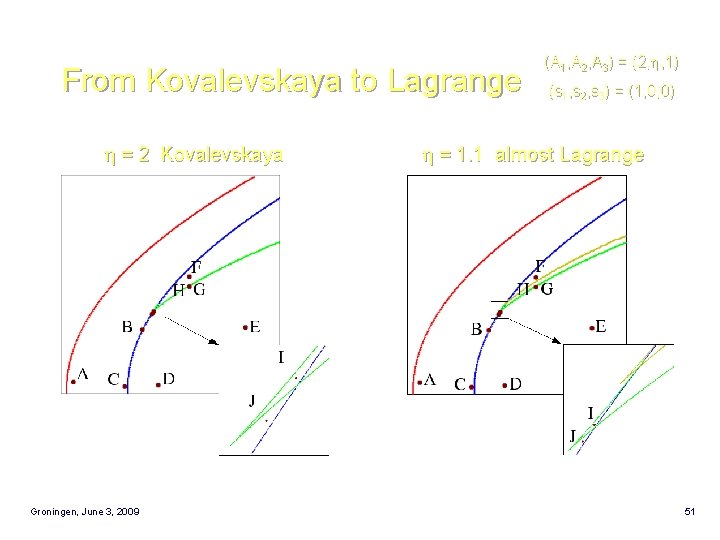
From Kovalevskaya to Lagrange = 2 Kovalevskaya Groningen, June 3, 2009 (A 1, A 2, A 3) = (2, , 1) (s 1, s 2, s 3) = (1, 0, 0) = 1. 1 almost Lagrange 51

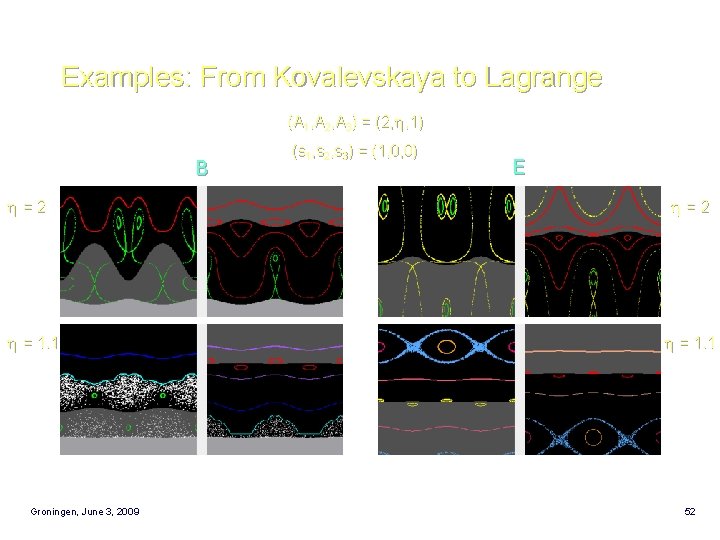
Examples: From Kovalevskaya to Lagrange (A 1, A 2, A 3) = (2, , 1) B =2 = 1. 1 Groningen, June 3, 2009 (s 1, s 2, s 3) = (1, 0, 0) E =2 = 1. 1 52

Example of a bifurcation scheme of periodic orbits Groningen, June 3, 2009 53