The complex dynamics of spinning tops Peter H

The complex dynamics of spinning tops Peter H. Richter University of Bremen Physics Colloquium Jacobs University Bremen February 23, 2011 Jacobs University Feb. 23, 2011 1

Outline Rigid bodies: configuration and parameter spaces - SO(3)→S 2, T 3→T 2 Moments of inertia, center of gravity, Cardan frame SO(3)-Dynamics - Euler-Poisson equations, Casimir and energy constants Relative equilibria (Staude solutions) and their stability (Grammel) Bifurcation diagrams, iso-energy surfaces Integrable cases: Euler, Lagrange, Kovalevskaya Liouville-Arnold foliation, critical tori, action representation General motion: Poincaré section over Poisson-spheres→torus T 3 -Dynamics - canonical equations 3 D or 5 D iso-energy surfaces Integrable cases: symmetric Euler and Lagrange in upright Cardan frame General motion: Poincaré section over Poisson-tori+2 cylinder connection Jacobs University Feb. 23, 2011 2

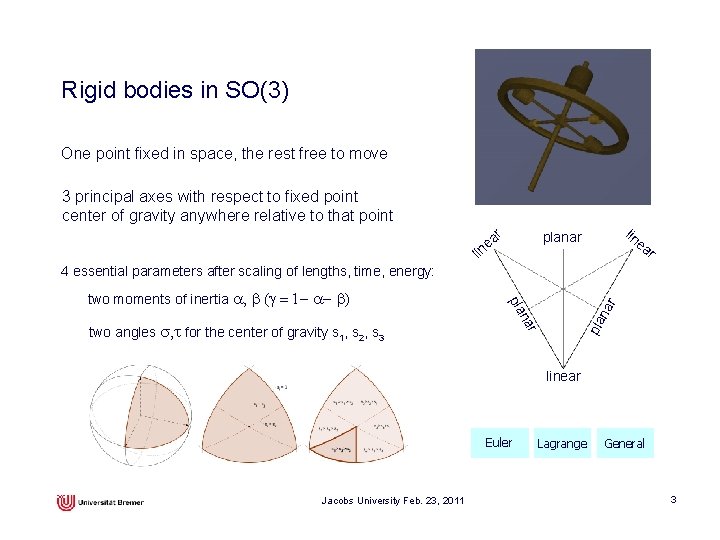
Rigid bodies in SO(3) One point fixed in space, the rest free to move 3 principal axes with respect to fixed point center of gravity anywhere relative to that point ar e n lin planar li ea r 4 essential parameters after scaling of lengths, time, energy: r two angles s, t for the center of gravity s 1, s 2, s 3 pla na na r pla two moments of inertia a, b (g = 1 - a- b) linear Euler Jacobs University Feb. 23, 2011 Lagrange General 3

Rigid bodies in T 3 a little more than 2 SO(3) → classical spin? Cardan angles (j, q, y) 6 essential parameters after scaling of lengths, time, energy: two moments of inertia a, b (g = 1 -a-b) at least one independent moment of inertia r for the Cardan frame (j + p, 2 p - q, y + p) Euler: symm up – Integr asymm up – Chaos Lagrange: up – Integr two angles s, t for the center of gravity angle d between the frame‘s axis and the direction of gravity tilted – Chaos General: horiz – Interm horiz – Chaos Jacobs University Feb. 23, 2011 4

SO(3)-Dynamics: Euler-Poisson equations coordinates angular velocity angular momentum Casimir constants → four-dimensional reduced phase space with parameter l energy constant Jacobs University Feb. 23, 2011 5

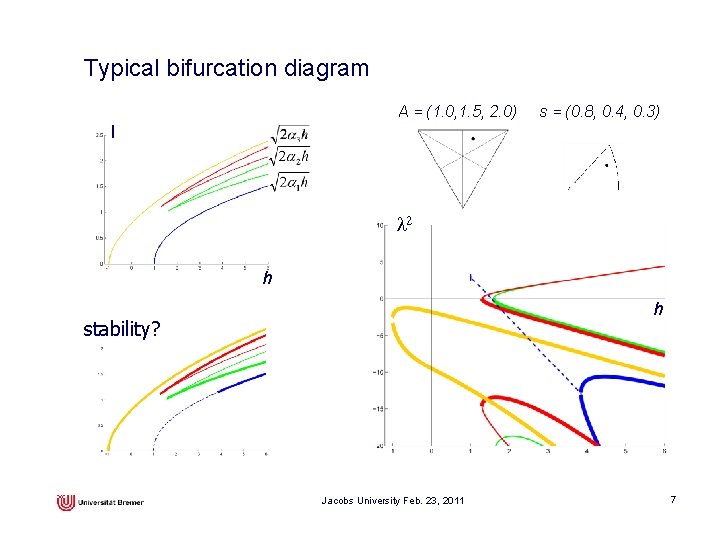
Relative equilibria: Staude solutions angular velocity vector constant, aligned with gravity high energy: rotations about principal axes low energy: rotations with hanging or upright position of center of gravity intermediate energy: carrousel motion possible only for certain combinations of (h, l ): bifurcation diagram Jacobs University Feb. 23, 2011 6

Typical bifurcation diagram A = (1. 0, 1. 5, 2. 0) s = (0. 8, 0. 4, 0. 3) l l 2 h h stability? Jacobs University Feb. 23, 2011 7

A Integrable cases P Euler: „gravity-free“ E 4 integrals Lagrange: „heavy“, symmetric 3 integrals L Kovalevskaya: 3 integrals Jacobs University Feb. 23, 2011 K 8

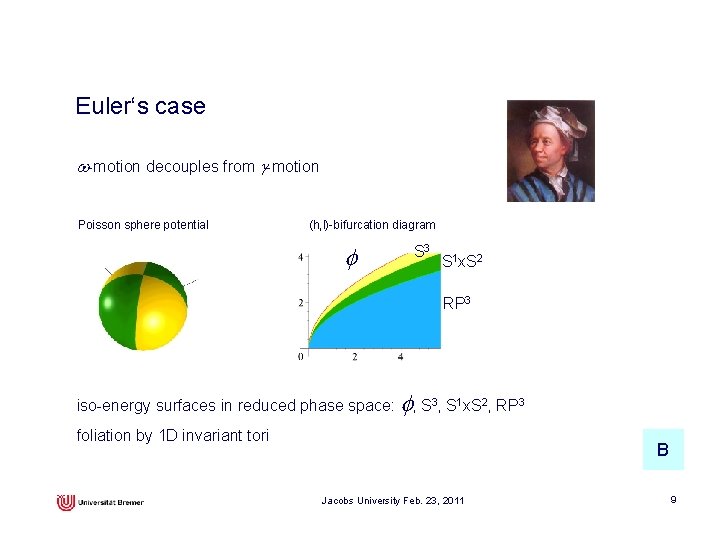
Euler‘s case w-motion decouples from g-motion Poisson sphere potential (h, l)-bifurcation diagram S 3 S 1 x. S 2 RP 3 iso-energy surfaces in reduced phase space: , S 3, S 1 x. S 2, RP 3 foliation by 1 D invariant tori B Jacobs University Feb. 23, 2011 9

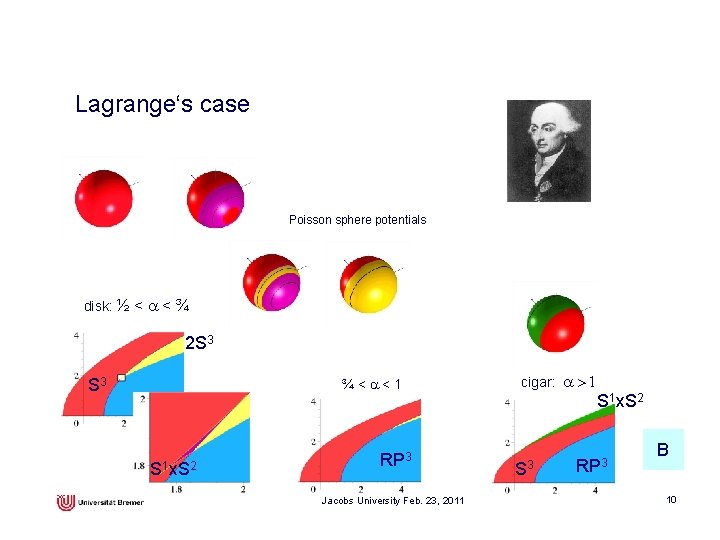
Lagrange‘s case Poisson sphere potentials disk: ½ < a < ¾ 2 S 3 ¾<a<1 S 1 x. S 2 RP 3 Jacobs University Feb. 23, 2011 cigar: a > 1 S 1 x. S 2 S 3 RP 3 B 10

Kovalevskaya‘s case Tori in phase space and Poincaré surface of section Action integral: B Jacobs University Feb. 23, 2011 11

Energy surfaces in action representation Euler Lagrange Kovalevskaya B Jacobs University Feb. 23, 2011 12

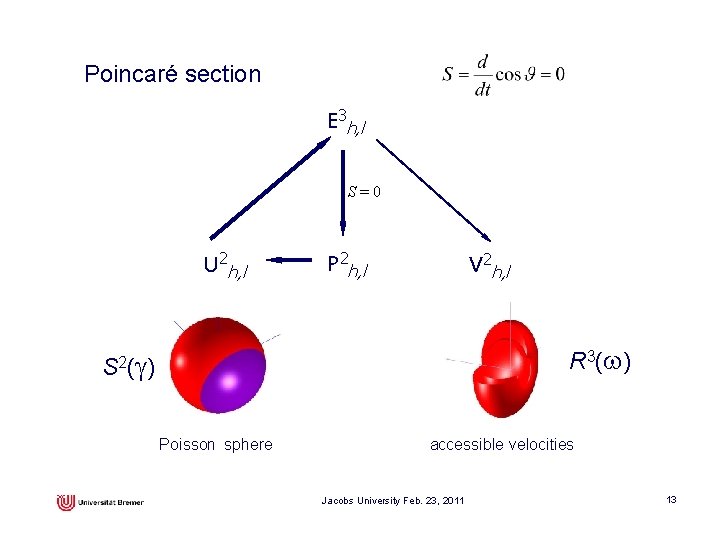
Poincaré section E 3 h, l S=0 U 2 h, l P 2 h, l V 2 h, l R 3 (w ) S 2 (g ) Poisson sphere accessible velocities Jacobs University Feb. 23, 2011 13

Topology of Surface of Section if lz is an integral SO(3)-Dynamics - 1: 1 projection to 2 copies of the Poisson sphere which are punctuated at their poles and glued along the polar circles this turns them into a torus (PP torus) at high energies the So. S covers the entire torus at lower energies boundary points on the two copies must be identified P T 3 -Dynamics - 1: 1 projection to 2 copies of the Poisson torus plus two connecting cylinders the Poincaré surface is not a manifold! but it allows for a complete picture at given energy h and angular momentum lz S Jacobs University Feb. 23, 2011 14

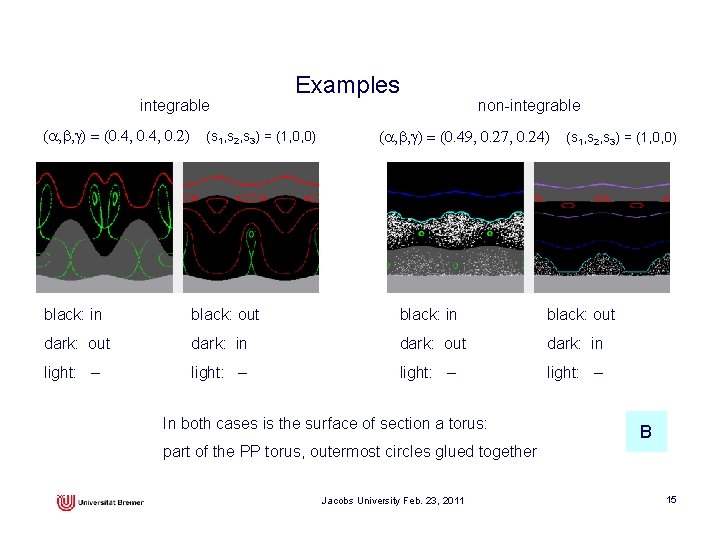
integrable (a, b, g) = (0. 4, 0. 2) Examples (s 1, s 2, s 3) = (1, 0, 0) non-integrable (a, b, g) = (0. 49, 0. 27, 0. 24) (s 1, s 2, s 3) = (1, 0, 0) black: in black: out dark: in light: – In both cases is the surface of section a torus: B part of the PP torus, outermost circles glued together Jacobs University Feb. 23, 2011 15

Summary • • Rigid bodies fixed in one point and subject to external forces need a support, e. g. a Cardan suspension This changes the configuration space from SO(3) to T 3, and the parameter set from 4 to 6 dimensional Integrable cases are only a small albeit highly interesting subset Not much is known about non-integrable cases If one degree of freedom is cyclic, complete Poincaré surfaces of section can be identified – always with SO(3), sometimes with T 3 The general case with 3 non-reducible degrees of freedom is beyond currently available methods of investigation Very little is known about the quantum mechanics of such systems Jacobs University Feb. 23, 2011 16

Thanks to • • Nadia Juhnke Andreas Wittek Holger Dullin Sven Schmidt Dennis Lorek Konstantin Finke Nils Keller Andreas Krut • • • Emil Horozov Mikhail Kharlamov Igor Gashenenko Alexey Bolsinov Alexander Veselov Victor Enolskii Jacobs University Feb. 23, 2011 17

Jacobs University Feb. 23, 2011 18

Stability analysis: variational equations (Grammel 1920) relative equilibrium: variational equations: J: a 6 x 6 matrix with rank 4 and characteristic polynomial g 0 l 6 + g 1 l 4 + g 2 l 2 Jacobs University Feb. 23, 2011 19

Stability analysis: eigenvalues 2 eigenvalues l = 0 4 eigenvalues obtained from g 0 l 4 + g 1 l 2 + g 2 = 0 The two l 2 are either real or complex conjugate. If the l 2 form a complex pair, two l have positive real part → instability If one l 2 is positive, then one of its roots l is positive → instability Linear stability requires both solutions l 2 to be negative: then all l are imaginary We distinguish singly and doubly unstable branches of the bifurcation diagram depending on whether one or two l 2 are non-negative Jacobs University Feb. 23, 2011 20

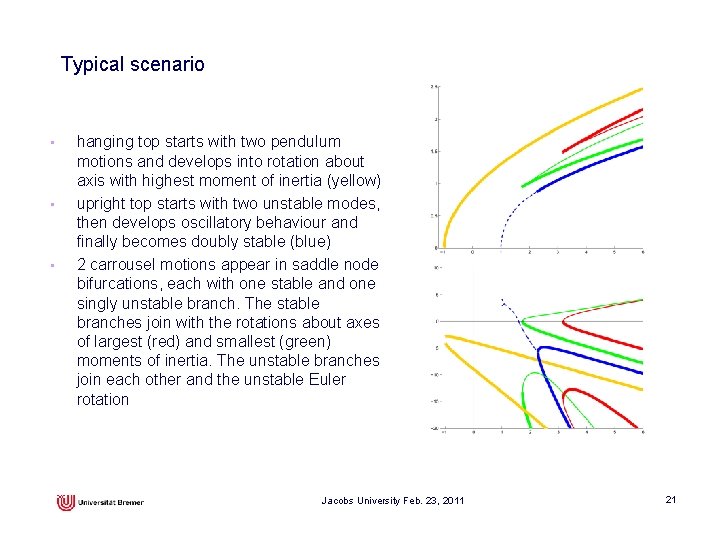
Typical scenario • • • hanging top starts with two pendulum motions and develops into rotation about axis with highest moment of inertia (yellow) upright top starts with two unstable modes, then develops oscillatory behaviour and finally becomes doubly stable (blue) 2 carrousel motions appear in saddle node bifurcations, each with one stable and one singly unstable branch. The stable branches join with the rotations about axes of largest (red) and smallest (green) moments of inertia. The unstable branches join each other and the unstable Euler rotation Jacobs University Feb. 23, 2011 21

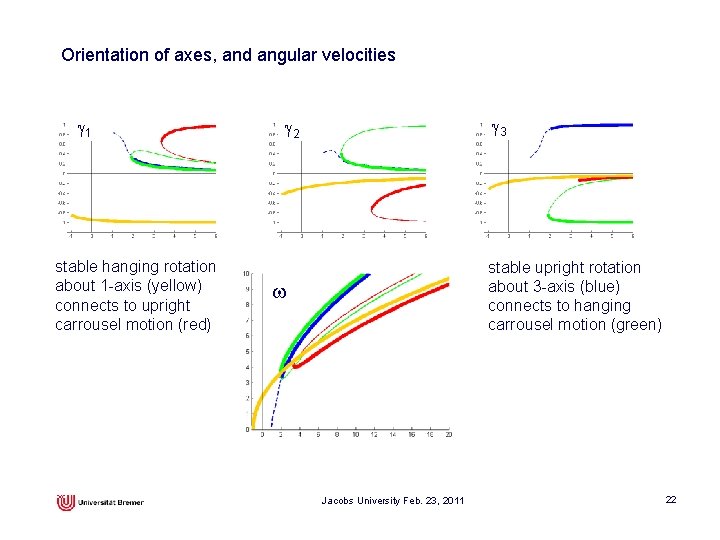
Orientation of axes, and angular velocities g 1 stable hanging rotation about 1 -axis (yellow) connects to upright carrousel motion (red) g 3 g 2 unstable carrousel motion about w 2 -axis (red and green) connects to stable branches Jacobs University Feb. 23, 2011 stable upright rotation about 3 -axis (blue) connects to hanging carrousel motion (green) 22

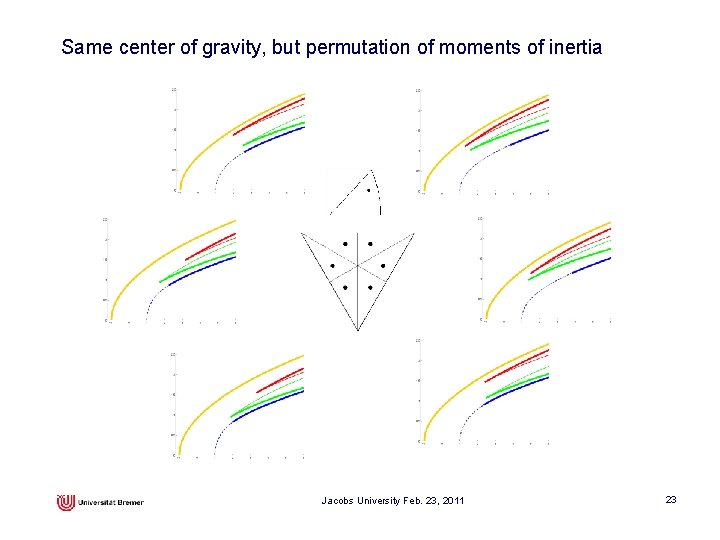
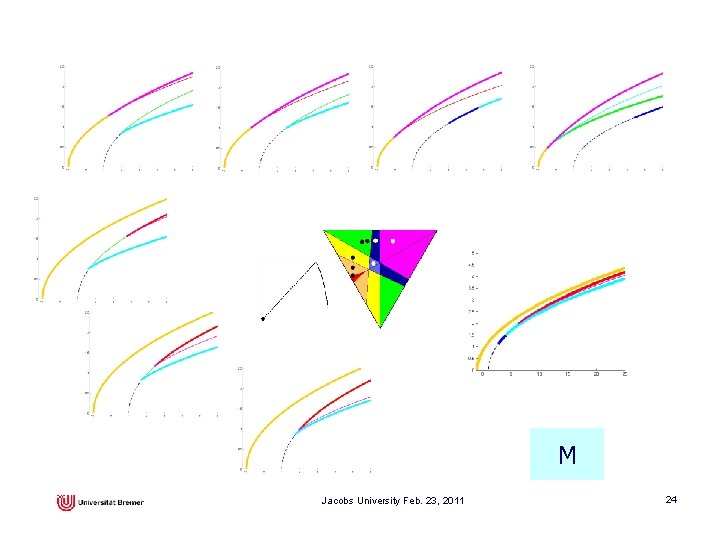
Same center of gravity, but permutation of moments of inertia Jacobs University Feb. 23, 2011 23

M Jacobs University Feb. 23, 2011 24

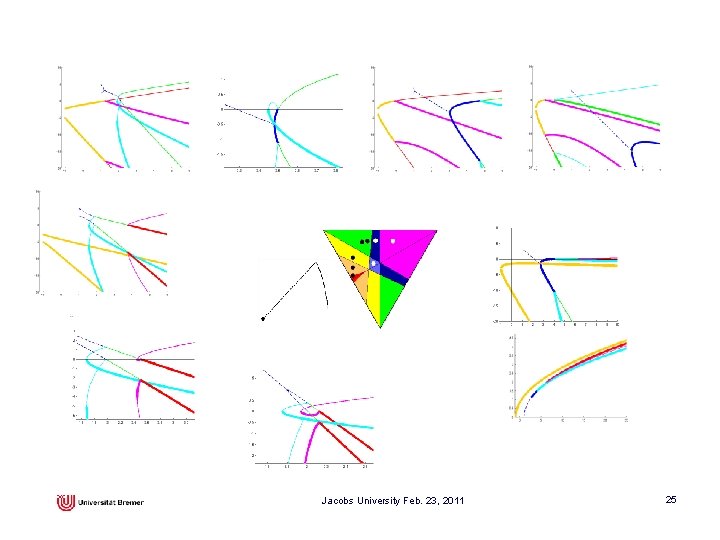
Jacobs University Feb. 23, 2011 25