The Complex Plane The Complex Plane The complex





















- Slides: 25

The Complex Plane

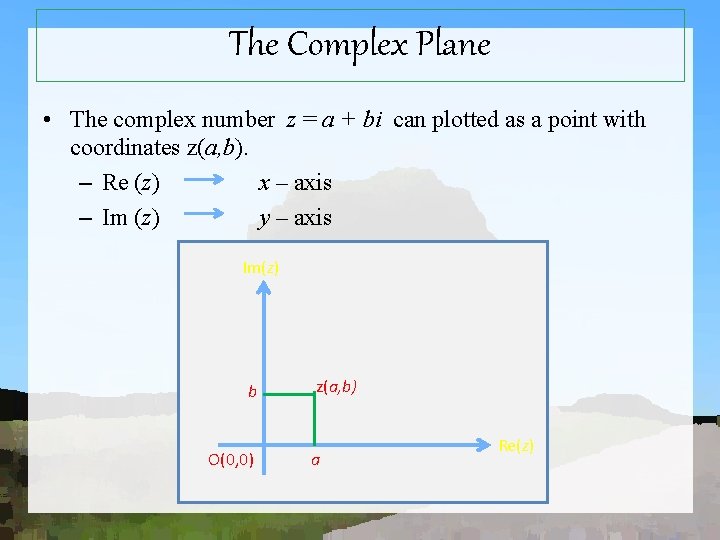
The Complex Plane • The complex number z = a + bi can plotted as a point with coordinates z(a, b). – Re (z) x – axis – Im (z) y – axis Im(z) b O(0, 0) z(a, b) a Re(z)

The Complex Plane • Definition 1. 6 (Modulus of Complex Numbers) The modulus of z is defined by Im(z) z(a, b) b r O(0, 0) a Re(z)

The Complex Plane • Example 1. 7 : • Find the modulus of z:

The Complex Plane • The Properties of Modulus

Argument of Complex Numbers • Definition 1. 7 The argument of the complex number z = a + bi is defined as 2 nd QUADRANT 1 st QUADRANT 3 rd QUADRANT 4 th QUADRANT

Argument of Complex Numbers • Example 1. 8 : • Find the arguments of z:

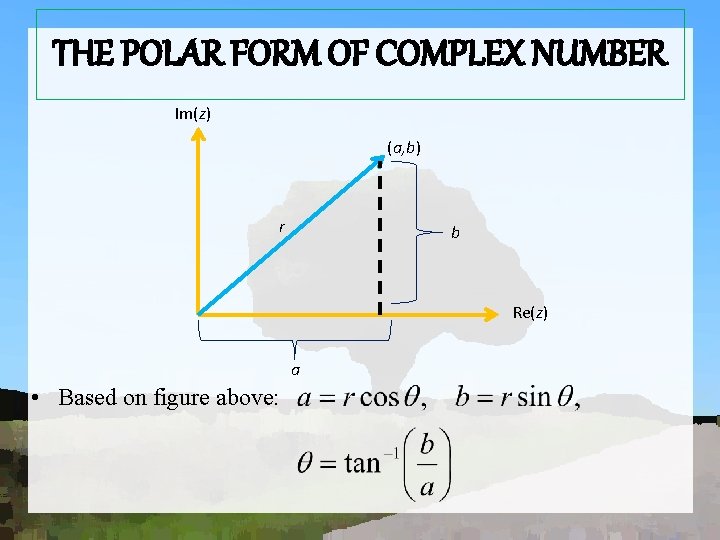
THE POLAR FORM OF COMPLEX NUMBER Im(z) (a, b) r b Re(z) a • Based on figure above:

• The polar form is defined by: • Example 1. 9: • Represent the following complex number in polar form:

• Example 1. 10 : • Express the following in standard form of complex number:

Theorem 1: If z 1 and z 2 are 2 complex numbers in polar form where then,

• Example 1. 11 : a) If z 1 = 2(cos 40+isin 40) and z 2 = 3(cos 95+isin 95). Find : b) If z 1 = 6(cos 60+isin 60) and z 2 = 2(cos 270+isin 270). Find :

THE EXPONENTIAL FORM • DEFINITION 1. 8 The exponential form of a complex number can be defined as Where θ is measured in radians and

THE EXPONENTIAL FORM • Example 1. 15 Express the complex number in exponential form:

THE EXPONENTIAL FORM Theorem 2 If and , then:

THE EXPONENTIAL FORM • Example 1. 16 If and , find:

DE MOIVRE’S THEOREM Theorem 3 If any power of n, then De Moivre’s Theorem: Therefore : is a complex number in polar form to

DE MOIVRE’S THEOREM • Example 1. 17 If , calculate :

FINDING ROOTS Theorem 4 If (θ in degrees) OR (θ in radians) Where k = 0, 1, 2, . . n-1 then, the n root of z is:

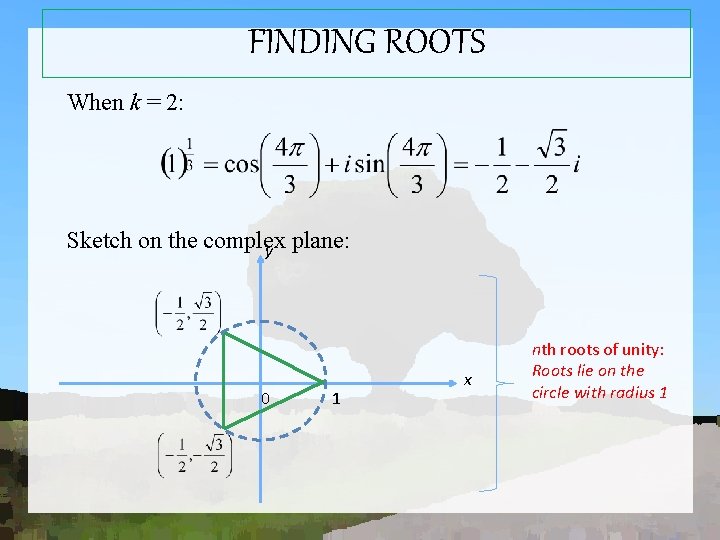
FINDING ROOTS Example 1. 18 If then, r =1 and Let n =3, therefore k =0, 1, 2 When k =0: When k = 1: :

FINDING ROOTS When k = 2: Sketch on the complex y plane: 0 1 x nth roots of unity: Roots lie on the circle with radius 1

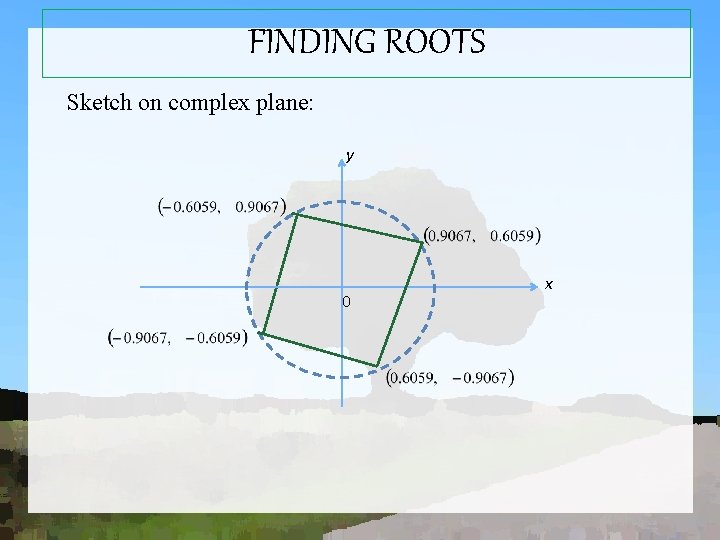
FINDING ROOTS Example 1. 18 If then, Let n =4, therefore k =0, 1, 2, 3 When k =0: When k = 1: and :

FINDING ROOTS Let n =4, therefore k =0, 1, 2, 3 When k =2: When k = 3:

FINDING ROOTS Sketch on complex plane: y 0 x

Thank You Prepared By Smt. Sasmita kumari swain Lecturer in Mathematics Khemundi College
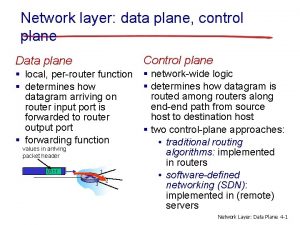
 Software-defined networking: a comprehensive survey
Software-defined networking: a comprehensive survey Forwarding equivalence classes
Forwarding equivalence classes Z-transform examples
Z-transform examples 탄성계수
탄성계수 Integration in the complex plane
Integration in the complex plane Compound complex simple sentences quiz
Compound complex simple sentences quiz Freud complexes
Freud complexes Simple compound complex and compound-complex sentences quiz
Simple compound complex and compound-complex sentences quiz The freudian concept of the ego is best described as *
The freudian concept of the ego is best described as * Droplet infection
Droplet infection Sublimation defense mechanism
Sublimation defense mechanism Tỉ lệ cơ thể trẻ em
Tỉ lệ cơ thể trẻ em đại từ thay thế
đại từ thay thế Các châu lục và đại dương trên thế giới
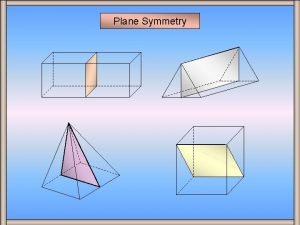
Các châu lục và đại dương trên thế giới Vẽ hình chiếu vuông góc của vật thể sau
Vẽ hình chiếu vuông góc của vật thể sau Thế nào là hệ số cao nhất
Thế nào là hệ số cao nhất Thế nào là mạng điện lắp đặt kiểu nổi
Thế nào là mạng điện lắp đặt kiểu nổi Dạng đột biến một nhiễm là
Dạng đột biến một nhiễm là Lời thề hippocrates
Lời thề hippocrates Hát kết hợp bộ gõ cơ thể
Hát kết hợp bộ gõ cơ thể Vẽ hình chiếu đứng bằng cạnh của vật thể
Vẽ hình chiếu đứng bằng cạnh của vật thể Cách giải mật thư tọa độ
Cách giải mật thư tọa độ Tư thế worm breton
Tư thế worm breton Sự nuôi và dạy con của hổ
Sự nuôi và dạy con của hổ điện thế nghỉ
điện thế nghỉ Thể thơ truyền thống
Thể thơ truyền thống