EE2402009 PCA EE2402009 PCA Principal Component Analysis EE2402009

EE-240/2009 PCA EE-240/2009

PCA Principal Component Analysis EE-240/2009

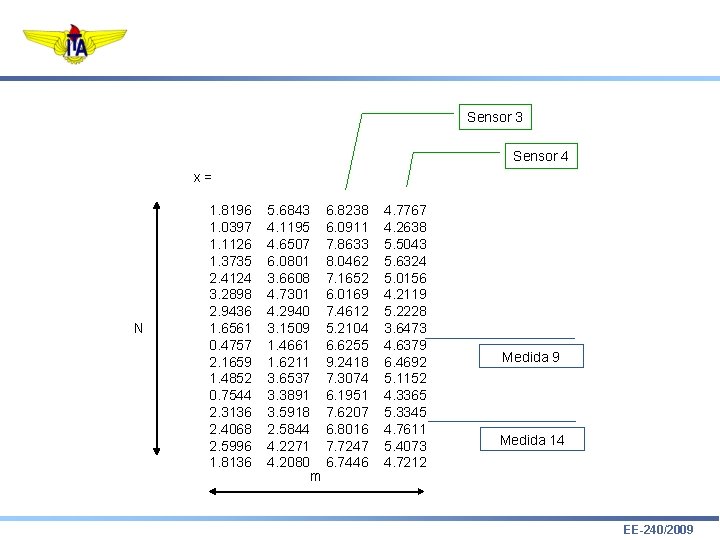
Sensor 3 Sensor 4 x= N 1. 8196 1. 0397 1. 1126 1. 3735 2. 4124 3. 2898 2. 9436 1. 6561 0. 4757 2. 1659 1. 4852 0. 7544 2. 3136 2. 4068 2. 5996 1. 8136 5. 6843 4. 1195 4. 6507 6. 0801 3. 6608 4. 7301 4. 2940 3. 1509 1. 4661 1. 6211 3. 6537 3. 3891 3. 5918 2. 5844 4. 2271 4. 2080 m 6. 8238 6. 0911 7. 8633 8. 0462 7. 1652 6. 0169 7. 4612 5. 2104 6. 6255 9. 2418 7. 3074 6. 1951 7. 6207 6. 8016 7. 7247 6. 7446 4. 7767 4. 2638 5. 5043 5. 6324 5. 0156 4. 2119 5. 2228 3. 6473 4. 6379 6. 4692 5. 1152 4. 3365 5. 3345 4. 7611 5. 4073 4. 7212 Medida 9 Medida 14 EE-240/2009

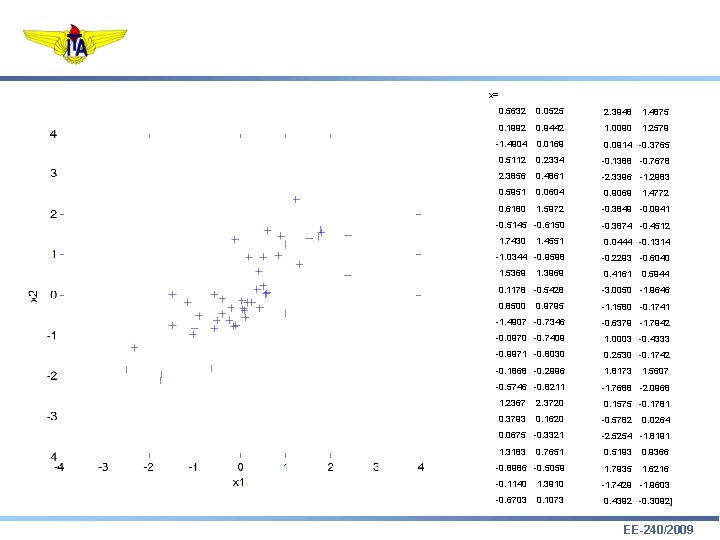
x= 0. 5632 0. 0525 2. 3948 1. 4875 0. 1992 0. 9442 1. 0090 1. 2579 -1. 4904 0. 0169 0. 0914 -0. 3765 0. 5112 0. 2334 -0. 1388 -0. 7678 2. 3856 0. 4861 -2. 3396 -1. 2983 0. 5951 0. 0604 0. 9069 0. 6180 1. 5972 -0. 3849 -0. 0941 -0. 5145 -0. 6150 -0. 3874 -0. 4512 1. 7430 1. 4551 0. 0444 -0. 1314 -1. 0344 -0. 9598 -0. 2293 -0. 6040 1. 5369 0. 4161 1. 3969 1. 4772 0. 5944 0. 1178 -0. 5428 -3. 0050 -1. 9646 0. 8500 0. 9795 -1. 1580 -0. 1741 -1. 4907 -0. 7346 -0. 6379 -1. 7942 -0. 0970 -0. 7409 1. 0003 -0. 4333 -0. 9971 -0. 8030 0. 2530 -0. 1742 -0. 1868 -0. 2996 1. 8173 -0. 5746 -0. 8211 -1. 7688 -2. 0968 1. 2367 2. 3720 0. 1575 -0. 1781 0. 3793 0. 1620 -0. 5782 1. 5607 0. 0264 0. 0675 -0. 3321 -2. 5254 -1. 8191 1. 3183 0. 7651 0. 5193 0. 9366 -0. 8986 -0. 5059 1. 7935 1. 6216 -0. 1140 1. 3910 -1. 7429 -1. 9603 -0. 6703 0. 1073 0. 4392 -0. 3092] EE-240/2009

clear all; N=50; sigma 2=[1 0. 8 ; 0. 8 1]; mi=repmat([0 0], N, 1); xx=mvnrnd(mi, sigma 2); xmean=mean(xx, 1); [lin, col]=size(xx); x=xx-repmat(xmean, lin, 1); [p, lat, exp]=pcacov(x); plot(x(: , 1), x(: , 2), '+'); hold on plot([p(1, 1) 0 p(1, 2)], [p(2, 1) 0 p(2, 2)]) EE-240/2009

EE-240/2009

EE-240/2009

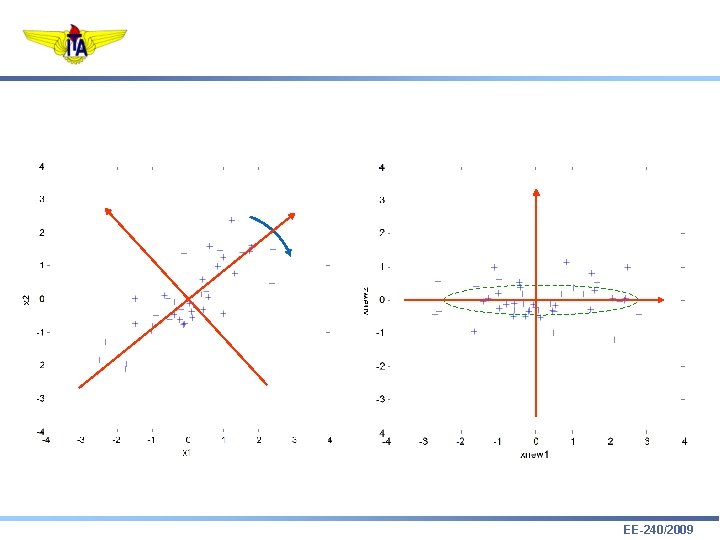
Como determinar? EE-240/2009

cov = [1 0 ; 0 1] cov=[1 0. 9 ; 0. 9 1] EE-240/2009

cov = [1 0 ; 0 1] cov=[1 0. 9 ; 0. 9 1] EE-240/2009

cov = [1 0 ; 0 1] cov=[1 0. 9 ; 0. 9 1] EE-240/2009

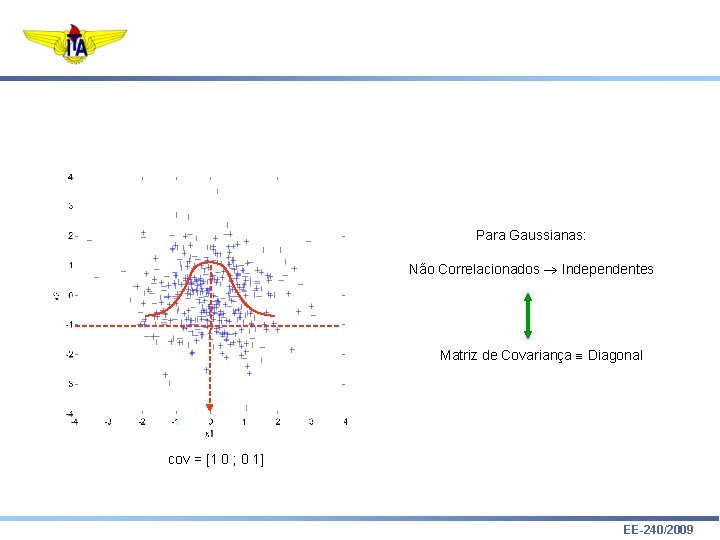
Para Gaussianas: Não Correlacionados Independentes Matriz de Covariança Diagonal cov = [1 0 ; 0 1] EE-240/2009

Dado XN m Obter P, tal que Y = XP Dada uma matriz Am m , os auto-valores e os auto-vetores v são caracterizados por ou seja, é diagonal. Como (s) é um polinômio de grau m, (s) =0 possui m raízes, 1, 2, . . . , m associados a v 1, v 2, . . . , vm No caso de e-valores distintos: P-1 A P = L EE-240/2009

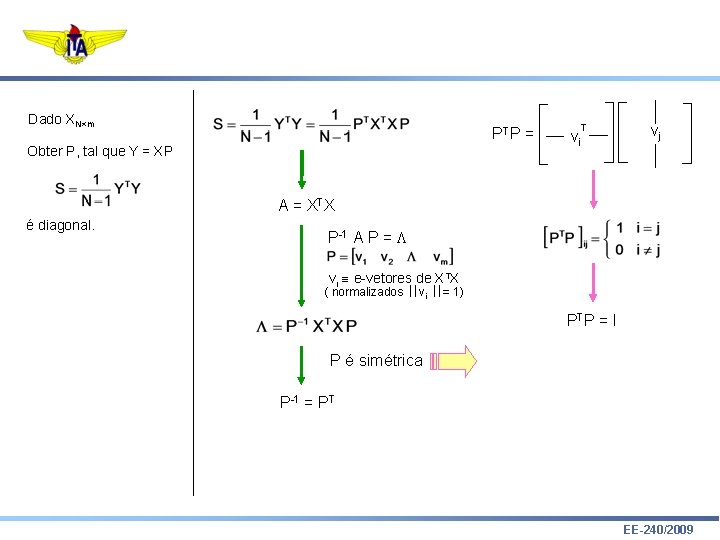
Dado XN m PT P = Obter P, tal que Y = XP A = XTX é diagonal. vj T vi i=j P-1 A P = L vi e-vetores de XTX ( normalizados vi = 1) P é simétrica P-1 = PT EE-240/2009

Dado XN m PT P = Obter P, tal que Y = XP vj T vi i j A = XTX é diagonal. P-1 A P = L vi e-vetores de XTX ( normalizados vi = 1) PT = P P é simétrica P-1 = PT EE-240/2009

Dado XN m PT P = Obter P, tal que Y = XP T vi vj A = XTX é diagonal. P-1 A P = L vi e-vetores de XTX ( normalizados vi = 1) PT P = I P é simétrica P-1 = PT EE-240/2009

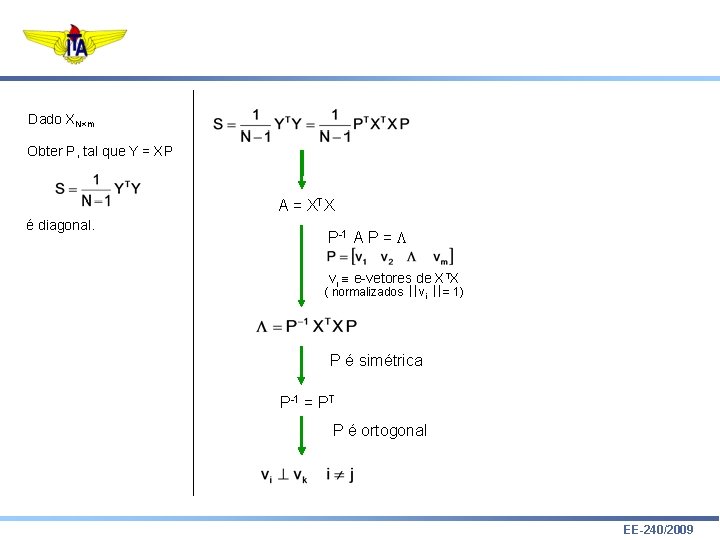
Dado XN m Obter P, tal que Y = XP A = XTX é diagonal. P-1 A P = L vi e-vetores de XTX ( normalizados vi = 1) P é simétrica P-1 = PT P é ortogonal EE-240/2009

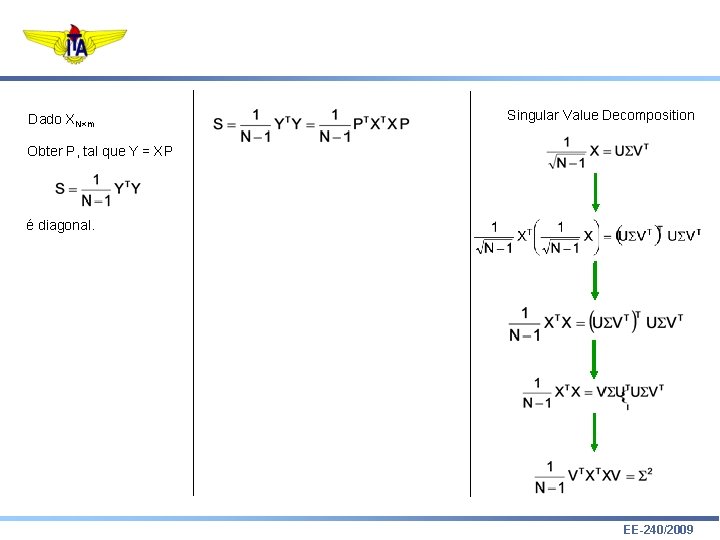
Dado XN m Singular Value Decomposition Obter P, tal que Y = XP é diagonal. EE-240/2009

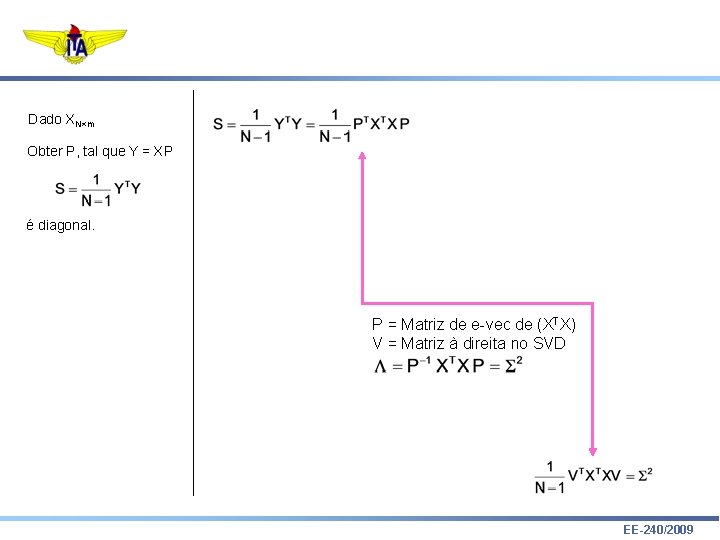
Dado XN m Obter P, tal que Y = XP é diagonal. P = Matriz de e-vec de (XTX) V = Matriz à direita no SVD EE-240/2009

x= 0. 5632 0. 0525 0. 1992 0. 9442 1. 0090 -1. 4904 0. 0169 0. 0914 -0. 3765 0. 5112 0. 2334 -0. 1388 -0. 7678 2. 3856 0. 4861 -2. 3396 -1. 2983 0. 5951 0. 0604 0. 9069 0. 6180 1. 5972 -0. 3849 -0. 0941 -0. 5145 -0. 6150 -0. 3874 -0. 4512 1. 7430 1. 4551 0. 0444 -0. 1314 -1. 0344 -0. 9598 -0. 2293 -0. 6040 1. 5369 0. 4161 1. 3969 2. 3948 1. 4875 1. 2579 1. 4772 0. 5944 0. 1178 -0. 5428 -3. 0050 -1. 9646 0. 8500 0. 9795 -1. 1580 -0. 1741 -1. 4907 -0. 7346 -0. 6379 -1. 7942 -0. 0970 -0. 7409 1. 0003 -0. 4333 -0. 9971 -0. 8030 0. 2530 -0. 1742 -0. 1868 -0. 2996 1. 8173 -0. 5746 -0. 8211 -1. 7688 -2. 0968 1. 2367 2. 3720 0. 1575 -0. 1781 0. 3793 0. 1620 -0. 5782 1. 5607 0. 0264 0. 0675 -0. 3321 -2. 5254 -1. 8191 1. 3183 0. 7651 0. 5193 0. 9366 -0. 8986 -0. 5059 1. 7935 1. 6216 -0. 1140 1. 3910 -1. 7429 -1. 9603 -0. 6703 0. 1073 0. 4392 -0. 3092] EE-240/2009

x= xx = 70. 3445 50. 3713 55. 6982 >> [P, Lambda]=eig(xx) P= Lambda = -0. 7563 0. 6543 -0. 7563 113. 9223 0 0 12. 1205 >> Lambda = inv(P)*xx*P OK Lambda = 113. 9223 0 0. 0000 12. 1205 Lambda (1) >> Lambda (2) 0. 5632 0. 0525 0. 1992 0. 9442 1. 0090 -1. 4904 0. 0169 0. 0914 -0. 3765 0. 5112 0. 2334 -0. 1388 -0. 7678 2. 3856 0. 4861 -2. 3396 -1. 2983 0. 5951 0. 0604 0. 9069 0. 6180 1. 5972 -0. 3849 -0. 0941 -0. 5145 -0. 6150 -0. 3874 -0. 4512 1. 7430 1. 4551 0. 0444 -0. 1314 -1. 0344 -0. 9598 -0. 2293 -0. 6040 1. 5369 0. 4161 1. 3969 2. 3948 1. 4875 1. 2579 1. 4772 0. 5944 0. 1178 -0. 5428 -3. 0050 -1. 9646 0. 8500 0. 9795 -1. 1580 -0. 1741 -1. 4907 -0. 7346 -0. 6379 -1. 7942 -0. 0970 -0. 7409 1. 0003 -0. 4333 -0. 9971 -0. 8030 0. 2530 -0. 1742 -0. 1868 -0. 2996 1. 8173 -0. 5746 -0. 8211 -1. 7688 -2. 0968 1. 2367 2. 3720 0. 1575 -0. 1781 0. 3793 0. 1620 -0. 5782 1. 5607 0. 0264 0. 0675 -0. 3321 -2. 5254 -1. 8191 1. 3183 0. 7651 0. 5193 0. 9366 -0. 8986 -0. 5059 1. 7935 1. 6216 -0. 1140 1. 3910 -1. 7429 -1. 9603 -0. 6703 0. 1073 0. 4392 -0. 3092] EE-240/2009

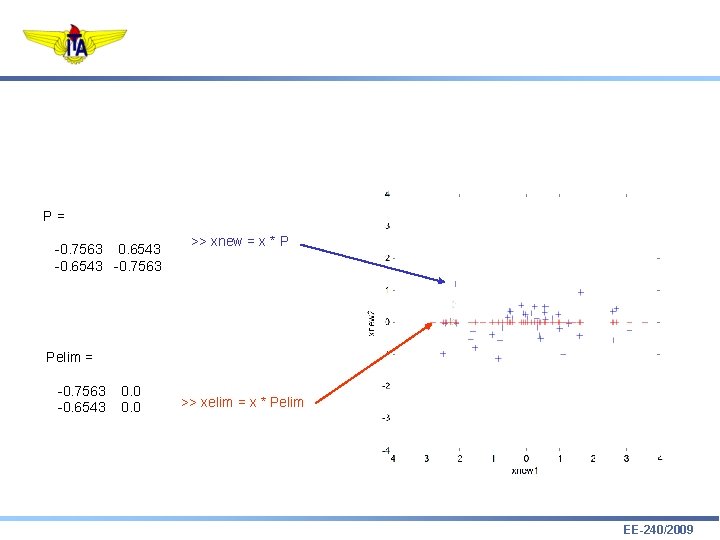
P= -0. 7563 0. 6543 -0. 7563 >> xnew = x * P Pelim = -0. 7563 -0. 6543 0. 0 >> xelim = x * Pelim EE-240/2009

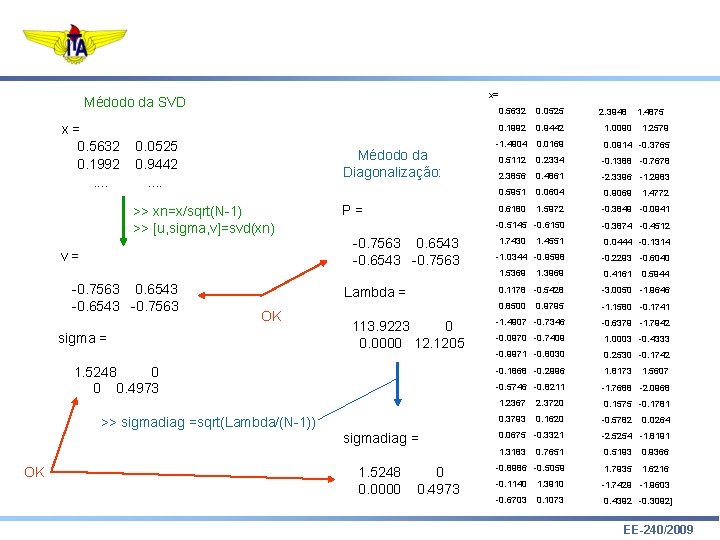
x= Médodo da SVD x= 0. 5632 0. 1992. . 0. 0525 0. 9442. . Médodo da Diagonalização: >> xn=x/sqrt(N-1) >> [u, sigma, v]=svd(xn) P= -0. 7563 0. 6543 -0. 7563 v= -0. 7563 0. 6543 -0. 7563 Lambda = OK sigma = 113. 9223 0 0. 0000 12. 1205 1. 5248 0 0 0. 4973 >> sigmadiag =sqrt(Lambda/(N-1)) sigmadiag = OK 1. 5248 0. 0000 0 0. 4973 0. 5632 0. 0525 0. 1992 0. 9442 1. 0090 -1. 4904 0. 0169 0. 0914 -0. 3765 0. 5112 0. 2334 -0. 1388 -0. 7678 2. 3856 0. 4861 -2. 3396 -1. 2983 0. 5951 0. 0604 0. 9069 0. 6180 1. 5972 -0. 3849 -0. 0941 -0. 5145 -0. 6150 -0. 3874 -0. 4512 1. 7430 1. 4551 0. 0444 -0. 1314 -1. 0344 -0. 9598 -0. 2293 -0. 6040 1. 5369 0. 4161 1. 3969 2. 3948 1. 4875 1. 2579 1. 4772 0. 5944 0. 1178 -0. 5428 -3. 0050 -1. 9646 0. 8500 0. 9795 -1. 1580 -0. 1741 -1. 4907 -0. 7346 -0. 6379 -1. 7942 -0. 0970 -0. 7409 1. 0003 -0. 4333 -0. 9971 -0. 8030 0. 2530 -0. 1742 -0. 1868 -0. 2996 1. 8173 -0. 5746 -0. 8211 -1. 7688 -2. 0968 1. 2367 2. 3720 0. 1575 -0. 1781 0. 3793 0. 1620 -0. 5782 1. 5607 0. 0264 0. 0675 -0. 3321 -2. 5254 -1. 8191 1. 3183 0. 7651 0. 5193 0. 9366 -0. 8986 -0. 5059 1. 7935 1. 6216 -0. 1140 1. 3910 -1. 7429 -1. 9603 -0. 6703 0. 1073 0. 4392 -0. 3092] EE-240/2009

>> help pcacov PCACOV Principal Component Analysis using the covariance matrix. [PC, LATENT, EXPLAINED] = PCACOV(X) takes a the covariance matrix, X, and returns the principal components in PC, the eigenvalues of the covariance matrix of X in LATENT, and the percentage of the total variance in the observations explained by each eigenvector in EXPLAINED. >> [pc, latent, explained]=pcacov(x) pc = -0. 7563 0. 6543 -0. 7563 latent = 10. 6734 3. 4814 explained = 75. 4046 24. 5954 EE-240/2009

>> help pcacov PCACOV Principal Component Analysis using the covariance matrix. [PC, LATENT, EXPLAINED] = PCACOV(X) takes a the covariance matrix, X, and returns the principal components in PC, the eigenvalues of the covariance matrix of X in LATENT, and the percentage of the total variance in the observations explained by each eigenvector in EXPLAINED. >> [pc, latent, explained]=pcacov(x) latent = pc = -0. 7563 0. 6543 -0. 7563 P= 10. 6734 3. 4814 explained = 75. 4046 24. 5954 v= -0. 7563 0. 6543 -0. 7563 OK EE-240/2009

>> help pcacov PCACOV Principal Component Analysis using the covariance matrix. [PC, LATENT, EXPLAINED] = PCACOV(X) takes a the covariance matrix, X, and returns the principal components in PC, the eigenvalues of the covariance matrix of X in LATENT, and the percentage of the total variance in the observations explained by each eigenvector in EXPLAINED. >> [pc, latent, explained]=pcacov(x) latent = pc = -0. 7563 0. 6543 -0. 7563 10. 6734 3. 4814 Lambda = 113. 9223 0 0 12. 1205 explained = 75. 4046 24. 5954 sqrlamb = >> sqrlamb=sqrt(evalor) 10. 6734 0 0 3. 4814 EE-240/2009

>> help pcacov PCACOV Principal Component Analysis using the covariance matrix. [PC, LATENT, EXPLAINED] = PCACOV(X) takes a the covariance matrix, X, and returns the principal components in PC, the eigenvalues of the covariance matrix of X in LATENT, and the percentage of the total variance in the observations explained by each eigenvector in EXPLAINED. >> [pc, latent, explained]=pcacov(x) pc = -0. 7563 0. 6543 -0. 7563 latent = 10. 6734 3. 4814 sqrlamb = 10. 6734 0 0 3. 4814 explained = 75. 4046 24. 5954 percent = >> e=[Lambda(1, 1) ; Lambda(2, 2)] >> soma=sum(e) >> percent=e*100/soma 75. 4046 24. 5954 EE-240/2009

>> help princomp PRINCOMP Principal Component Analysis (centered and scaled data). [PC, SCORE, LATENT, TSQUARE] = PRINCOMP(X) takes a data matrix X and returns the principal components in PC, the so-called Z-scores in SCORES, the eigenvalues of the covariance matrix of X in LATENT, and Hotelling's T-squared statistic for each data point in TSQUARE. >> [pc, score, latent 1, tsquare]=princomp(x) pc = -0. 7563 0. 6543 -0. 7563 score = -0. 4603 0. 3288 -0. 7684 -0. 5837 1. 1161 -0. 9879 -0. 5393 0. 1579 -2. 1222 1. 1932 -0. 4896 0. 3437. . latent 1 = 2. 3249 0. 2474 tsquare = 0. 5281 1. 6315 4. 4813 0. 2260 7. 6929 0. 5806. . . EE-240/2009

>> help princomp PRINCOMP Principal Component Analysis (centered and scaled data). [PC, SCORE, LATENT, TSQUARE] = PRINCOMP(X) takes a data matrix X and returns the principal components in PC, the so-called Z-scores in SCORES, the eigenvalues of the covariance matrix of X in LATENT, and Hotelling's T-squared statistic for each data point in TSQUARE. >> [pc, score, latent 1, tsquare]=princomp(x) pc = -0. 7563 0. 6543 -0. 7563 P= -0. 7563 0. 6543 -0. 7563 score = -0. 4603 0. 3288 -0. 7684 -0. 5837 1. 1161 -0. 9879 -0. 5393 0. 1579 -2. 1222 1. 1932 -0. 4896 0. 3437. . latent 1 = 2. 3249 0. 2474 tsquare = 0. 5281 1. 6315 4. 4813 0. 2260 7. 6929 0. 5806. . . EE-240/2009

>> help princomp PRINCOMP Principal Component Analysis (centered and scaled data). [PC, SCORE, LATENT, TSQUARE] = PRINCOMP(X) takes a data matrix X and returns the principal components in PC, the so-called Z-scores in SCORES, the eigenvalues of the covariance matrix of X in LATENT, and Hotelling's T-squared statistic for each data point in TSQUARE. >> [pc, score, latent 1, tsquare]=princomp(x) score = -0. 4603 0. 3288 -0. 7684 -0. 5837 1. 1161 -0. 9879 -0. 5393 0. 1579 -2. 1222 1. 1932 -0. 4896 0. 3437. . sco = >> sco=x*P -0. 4603 0. 3288 -0. 7684 -0. 5838 1. 1161 -0. 9880 -0. 5393 0. 1580 -2. 1223 1. 1933 -0. 4896 0. 3437 EE-240/2009

>> help princomp PRINCOMP Principal Component Analysis (centered and scaled data). [PC, SCORE, LATENT, TSQUARE] = PRINCOMP(X) takes a data matrix X and returns the principal components in PC, the so-called Z-scores in SCORES, the eigenvalues of the covariance matrix of X in LATENT, and Hotelling's T-squared statistic for each data point in TSQUARE. >> [pc, score, latent 1, tsquare]=princomp(x) pc = -0. 7563 0. 6543 -0. 7563 score = -0. 4603 0. 3288 -0. 7684 -0. 5837 1. 1161 -0. 9879 -0. 5393 0. 1579 -2. 1222 1. 1932 -0. 4896 0. 3437. . latent 1 = 2. 3249 0. 2474 >> eig( x'*x /(N-1)) ans = tsquare = 0. 5281 1. 6315 4. 4813 0. 2260 7. 6929 0. 5806. . . 0. 2474 2. 3249 EE-240/2009

>> help princomp PRINCOMP Principal Component Analysis (centered and scaled data). [PC, SCORE, LATENT, TSQUARE] = PRINCOMP(X) takes a data matrix X and returns the principal components in PC, the so-called Z-scores in SCORES, the eigenvalues of the covariance matrix of X in LATENT, and Hotelling's T-squared statistic for each data point in TSQUARE. >> [pc, score, latent 1, tsquare]=princomp(x) pc = -0. 7563 0. 6543 -0. 7563 score = -0. 4603 0. 3288 -0. 7684 -0. 5837 1. 1161 -0. 9879 -0. 5393 0. 1579 -2. 1222 1. 1932 -0. 4896 0. 3437. . latent 1 = 2. 3249 0. 2474 tsquare = 0. 5281 1. 6315 4. 4813 0. 2260 7. 6929 0. 5806. . . caracteriza a região de confiança 100 a% EE-240/2009

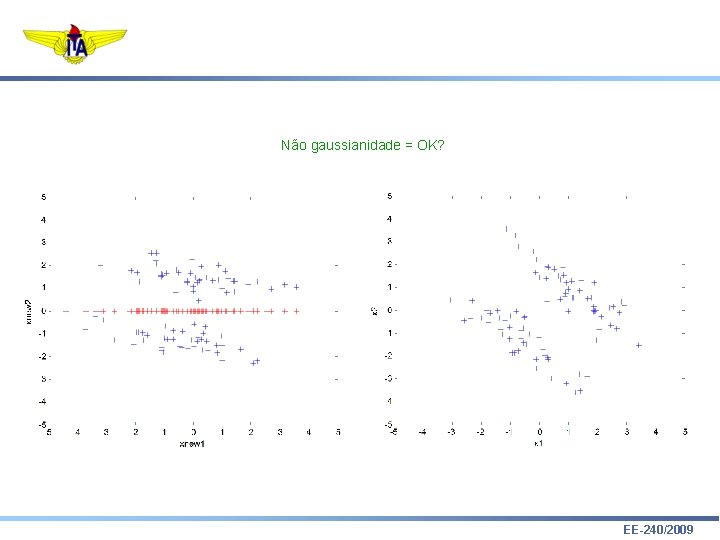
Não gaussianidade = OK? EE-240/2009

Não gaussianidade = OK? EE-240/2009

Não gaussianidade = OK? EE-240/2009

>> xm=mean(xx); >> [lin, col]=size(xx); >> xm=repmat(xm, lin, 1); >> xx=xx-xm; EE-240/2009

EE-240/2009

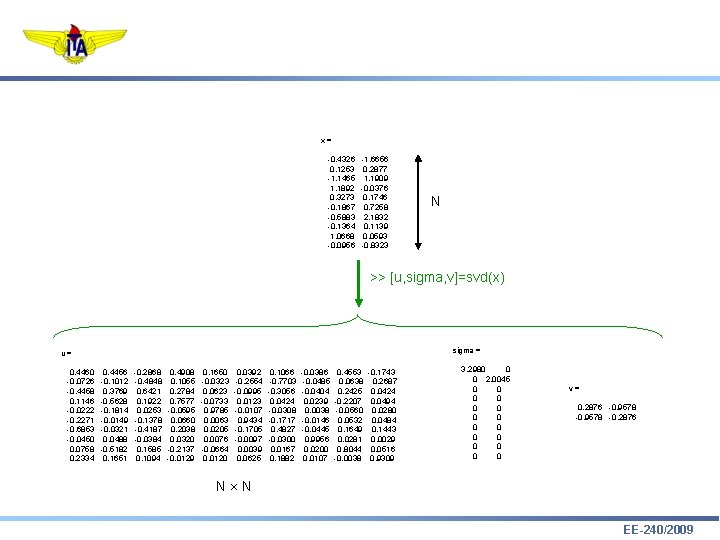
x= -0. 4326 -1. 6656 0. 1253 0. 2877 -1. 1465 1. 1909 1. 1892 -0. 0376 0. 3273 0. 1746 -0. 1867 0. 7258 -0. 5883 2. 1832 -0. 1364 0. 1139 1. 0668 0. 0593 -0. 0956 -0. 8323 N >> [u, sigma, v]=svd(x) sigma = u= 0. 4460 -0. 0726 -0. 4458 0. 1146 -0. 0222 -0. 2271 -0. 6853 -0. 0450 0. 0758 0. 2334 0. 4456 -0. 1012 0. 3769 -0. 5628 -0. 1814 -0. 0149 -0. 0321 0. 0488 -0. 5182 0. 1651 -0. 2868 -0. 4848 0. 6421 0. 1922 0. 0253 -0. 1378 -0. 4187 -0. 0384 0. 1585 0. 1094 0. 4908 0. 1055 0. 2784 0. 7577 -0. 0595 0. 0660 0. 2038 0. 0320 -0. 2137 -0. 0129 0. 1650 -0. 0323 0. 0623 -0. 0733 0. 9785 0. 0063 0. 0205 0. 0076 -0. 0664 0. 0120 0. 0392 -0. 2554 -0. 0995 0. 0123 -0. 0107 0. 9434 -0. 1705 -0. 0097 0. 0039 0. 0625 0. 1066 -0. 7703 -0. 3056 0. 0424 -0. 0308 -0. 1717 0. 4827 -0. 0300 0. 0167 0. 1882 -0. 0386 -0. 0485 -0. 0404 0. 0239 0. 0038 -0. 0146 -0. 0445 0. 9956 0. 0200 0. 0107 0. 4553 0. 0638 0. 2425 -0. 2207 -0. 0560 0. 0532 0. 1649 0. 0281 0. 8044 -0. 0038 -0. 1743 0. 2687 0. 0424 0. 0494 0. 0280 0. 0484 0. 1443 0. 0029 0. 0516 0. 9309 3. 2980 0 0 2. 0045 0 0 0 0 v= 0. 2876 -0. 9578 -0. 2876 N N EE-240/2009

Muito Obrigado! EE-240/2009