Principal Component Analysis PCA or Empirical Orthogonal Functions

Principal Component Analysis (PCA) or Empirical Orthogonal Functions (EOFs) Arnaud Czaja (SPAT Data analysis lecture Nov. 2011)

Outline • Motivation • Mathematical formulation (on the board) • Illustration: analysis of ~100 yr of sea surface temperature fluctuations in the North Atlantic • How to compute EOFs • Some issues regarding EOF analysis

Motivation 12 EOFs • Data compression. . . to “carry less luggage” Original pictures 6 EOFs 24 EOFs

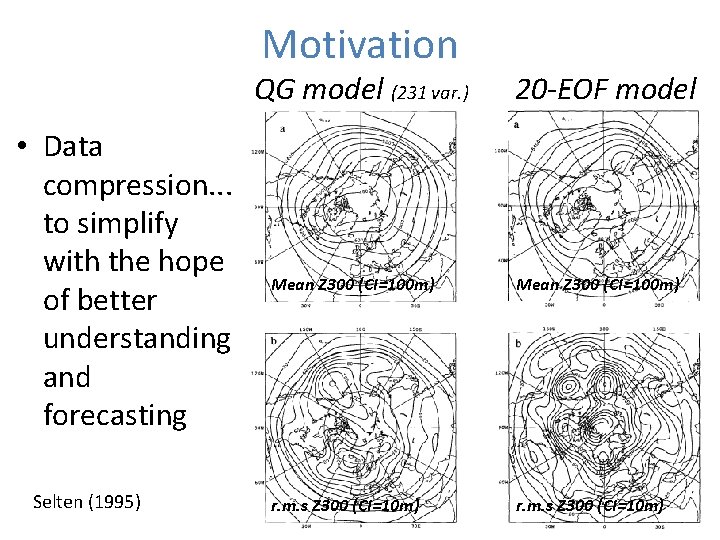
Motivation QG model (231 var. ) • Data compression. . . to simplify with the hope of better understanding and forecasting Selten (1995) 20 -EOF model Mean Z 300 (CI=100 m) r. m. s Z 300 (CI=10 m)

Motivation • Identify “modes” empirically from data “Annular modes” in pressure data Thompson and Wallace (2000)

Some examples of calculations

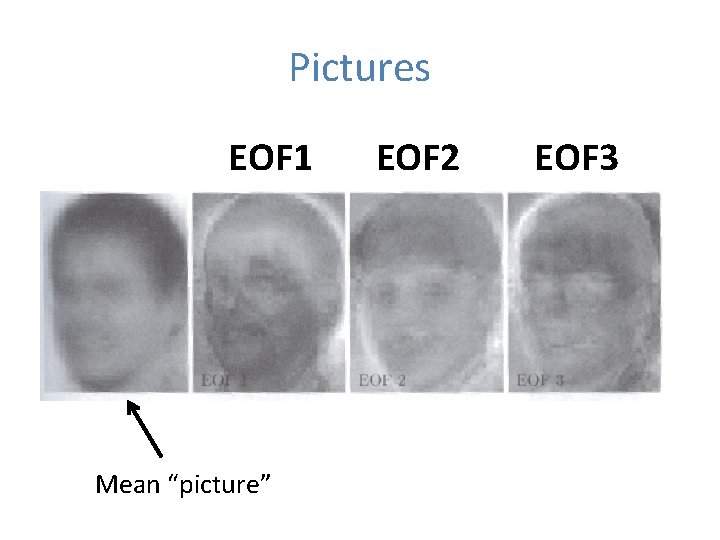
Pictures EOF 1 Mean “picture” EOF 2 EOF 3

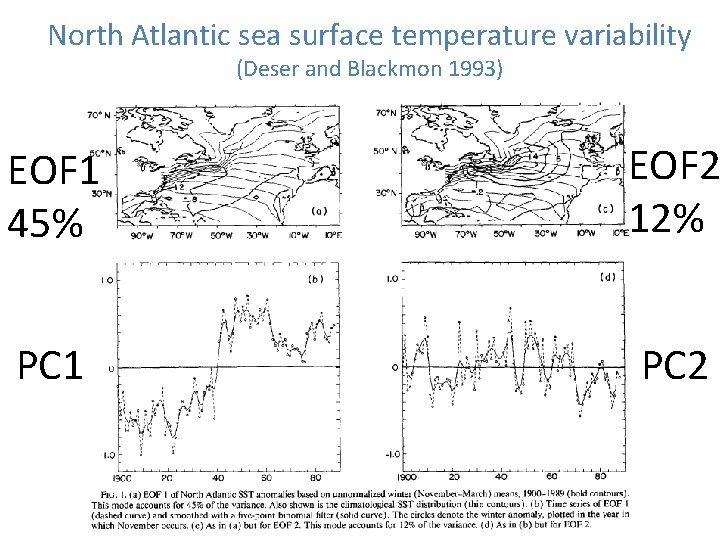
North Atlantic sea surface temperature variability (Deser and Blackmon 1993) EOF 1 45% EOF 2 12% PC 1 PC 2

How to compute EOFs • Compute the covariance matrix Σ of the observation matrix X • Compute its eigenvalues (variance explained) and eigenvectors (=eof) • The principal component is then obtained by “projection”: pc(t) = X * eof • Another (more efficient) method: singular value decomposition of X (come and see me if you are interested)

Main issues with EOF analysis • Sensitivity to size of dataset (“sampling” issues) See North et al. (1982)

Main issues with EOF analysis • Sensitivity to size of dataset (“sampling” issues)

Main issues with EOF analysis • Sensitivity to size of dataset (“sampling” issues)

Main issues with EOF analysis • Orthogonality constraint is not physical. Methods have been developed to deal with this (“rotated EOFs”) • The link between EOFs and physical modes of a system is not clear

Main issues with EOF analysis • Orthogonality constraint is not physical. Methods have been developed to deal with this (“rotated EOFs”) • The link between EOFs and physical modes of a system is not clear • Good luck if you try EOFs. . . Do not hesitate to come and see me!