FACTOR ANALYSIS 1 What is Factor Analysis FA

FACTOR ANALYSIS 1

What is Factor Analysis (FA)? • Method of data reduction o take many variables and explain them with a few “factors” or “components” o correlated variables are grouped together and separated from other variables with low or no correlation o seeks underlying unobservable (latent) variables that are reflected in the observed variables (manifest variables)

More on Factor Analysis • requires a large sample size since it is based on the correlation matrix of the variables involved o 50 cases is very poor o 100 is poor o 200 is fair o 300 is good o 500 is very good, and 1000 or more is excellent. o rule of thumb – a bare minimum of 10 observations per variable is necessary to avoid computational difficulties.

“Good Factor” • A good factor: o makes sense o easy to interpret o simple structure o lacks complex loadings

Problems with Factor Analysis • There is no statistical criterion to compare the linear combination to as in MANOVA or Canonical Correlations • It is more art than science o several extraction methods o several rotation methods o number of factors to extract o communality estimates • Life (researcher) saver o Often, when nothing else can be salvaged from research a FA will be conducted.

Types of Factor Analysis • Exploratory Factor Analysis (EFA) • Confirmatory Factor Analysis (CFA)

Exploratory Factor Analysis (EFA) • Exploratory Factor Analysis (EFA) o summarizing data by grouping correlated variables o investigating sets of measured variables related to theoretical constructs o usually done near the onset of research o generate “factor scores“ which represent values of the underlying constructs for use in other analyses o often confused with Principal Component Analysis (PCA) which is a similar statistical procedure

FA vs. PCA EFA PCA • analyzes only the variance • analyzes all of the variance shared among the variables (common variance without error or unique variance) • examines what are the underlying processes that could produce these correlations • produces factors • factors cause variables • only summarizes empirical associations • very data driven • produces components • components are aggregates of the variables

Confirmatory Factor Analysis (CFA) • Confirmatory FA o more advanced technique o used when factor structure is known or at least theorized o testing generalization of factor structure to new data, etc. o tested through Structural Equation Modeling (SEM) methods discussed later in course

Application of Factor Analysis defining indicators of constructs o ideally 4 or more measures should be chosen to represent each construct of interest o choice of measures should, as much as possible, be guided by theory, previous research, and logic selecting items or scales to be included in a measure determine what items or scales should be included and excluded from a measure results of the analysis should not be used alone in making decisions of inclusions or exclusions decisions should be taken in conjunction with theory and what is known about the construct(s) that the items or scales assess

Assumptions Underlying Factor Analysis • measured variables are linearly related to the factors + errors. o likely to be violated if items use limited response scales, i. e. too many dichotomous variables • should have a bivariate normal distribution for each pair of variables • observations are independent • assumes variables are determined by common factors and unique factors o unique factors assumed to be uncorrelated with each other and with the common factors

Terminology • Reproduced Correlation Matrix o correlation matrix based on the extracted factors o want the values in the reproduced matrix to be as close to the values in the original correlation matrix as possible o If reproduced matrix is very similar to the original correlation matrix, then the few factors do a good job of representing the original data • Residual Correlation Matrix • represents the differences between original correlations and the reproduced correlations • should be close to zero

Terminology • Eigenvalues o number of variables which the factor represents o amount of variance in the data described by the factor • Communalities o proportion of the variance in the original variables that can be explained by the factors o factor solution should explain at least half of each original variable's variance, so the communality value for each variable should be 0. 50 or higher

Terminology • Rotated Factor Matrix o represents both how the variables are weighted for each factor and also the correlation between the variables and the factor • these are correlations so possible values range from -1 to +1 o In SPSS, you can tell it to print any of the correlations that less than a particular value (usually use 0. 3) o makes the output easier to read by removing the clutter of low correlations that are probably not meaningful anyway

General Steps to FA • Step 1: Selecting and Measuring a set of variables in a given domain • Step 2: Data screening in order to prepare the correlation matrix • Step 3: Factor Extraction • Step 4: Factor Rotation to increase interpretability • Step 5: Interpretation • Further Steps: Validation and Reliability of the measures

The Correlation Matrix • generate a correlation matrix for all variables • identify variables not related to other variables • if correlation between variables are small, unlikely that they share common factors (variables must be related to each other for the factor model to be appropriate) • think of correlations in absolute value. • correlation coefficients > 0. 3 in absolute value are indicative of acceptable correlations. • examine visually the appropriateness of the factor model

The Correlation Matrix • Bartlett Test of Sphericity o tests the null hypothesis that the correlation matrix is an identity matrix (all diagonal terms are 1 and all offdiagonal terms are 0) § want to reject this null hypothesis o If the value of the test statistic for sphericity is large and the associated significance level is small, it is unlikely that the population correlation matrix is an identity

The Correlation Matrix • The Kaiser-Meyer-Olkin (KMO) measure of sampling adequacy o index for comparing magnitude of observed correlation coefficients to magnitude of partial correlation coefficients. o closer KMO measure is to 1, evidence of a sizeable sampling adequacy § 0. 8 and higher are great § 0. 7 is acceptable § 0. 6 is mediocre § < 0. 5 is unacceptable o Small KMO values indicate that a factor analysis may not be a good idea.

Factor Extraction primary objective is to determine the factors initial decisions can be made here about number of factors underlying a set of measured variables. several factor extraction methods o Principal Component Analysis – used for data reduction o Maximum likelihood method o Principal axis factoring o Alpha method o Unweighted lease squares method o Generalized least square method o Image factoring

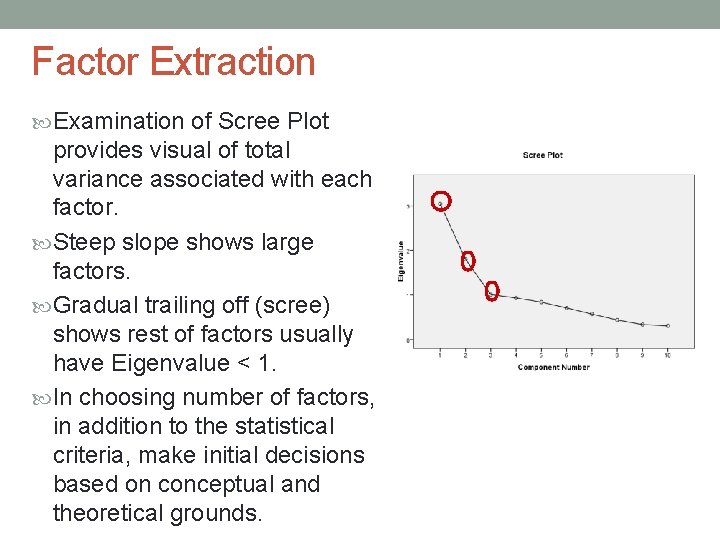
Factor Extraction To decide on how many factors needed to represent the data, use 2 statistical criteria: o Eigenvalues o Scree Plot Determination of number of factors is usually done by considering only factors with Eigenvalues > 1. Factors with a variance less than 1 are no better than a single variable, since each variable is expected to have a variance of 1. Total Variance Explained Extraction Sums of Squared Initial Eigenvalues Loadings % of Cumulativ Variance e % Comp onent Total 1 3. 046 30. 465 2 1. 801 18. 011 48. 476 3 1. 009 10. 091 58. 566 4 . 934 9. 336 67. 902 5 . 840 8. 404 76. 307 6 . 711 7. 107 83. 414 7 . 574 5. 737 89. 151 8 . 440 4. 396 93. 547 9 . 337 3. 368 96. 915 10 . 308 3. 085 100. 000 Extraction Method: Principal Component Analysis.

Factor Extraction Examination of Scree Plot provides visual of total variance associated with each factor. Steep slope shows large factors. Gradual trailing off (scree) shows rest of factors usually have Eigenvalue < 1. In choosing number of factors, in addition to the statistical criteria, make initial decisions based on conceptual and theoretical grounds.

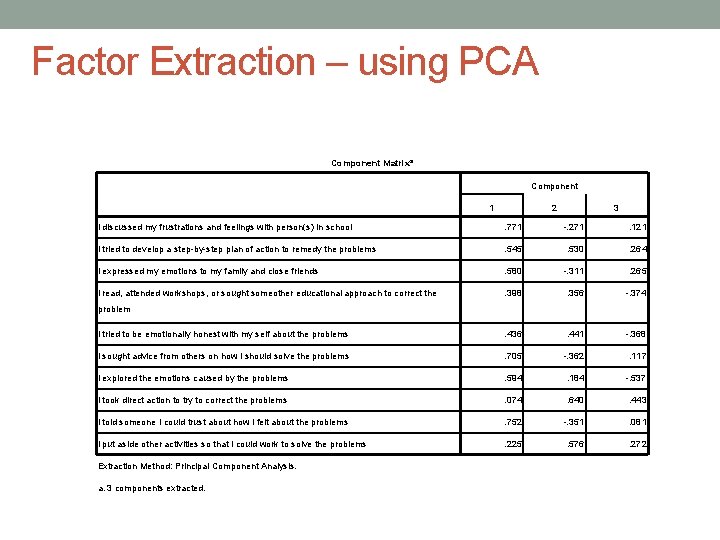
Factor Extraction – using PCA Component Matrixa Component 1 2 3 I discussed my frustrations and feelings with person(s) in school . 771 -. 271 . 121 I tried to develop a step-by-step plan of action to remedy the problems . 545 . 530 . 264 I expressed my emotions to my family and close friends . 580 -. 311 . 265 I read, attended workshops, or sought someother educational approach to correct the . 398 . 356 -. 374 I tried to be emotionally honest with my self about the problems . 436 . 441 -. 368 I sought advice from others on how I should solve the problems . 705 -. 362 . 117 I explored the emotions caused by the problems . 594 . 184 -. 537 I took direct action to try to correct the problems . 074 . 640 . 443 I told someone I could trust about how I felt about the problems . 752 -. 351 . 081 I put aside other activities so that I could work to solve the problems . 225 . 576 . 272 problem Extraction Method: Principal Component Analysis. a. 3 components extracted.

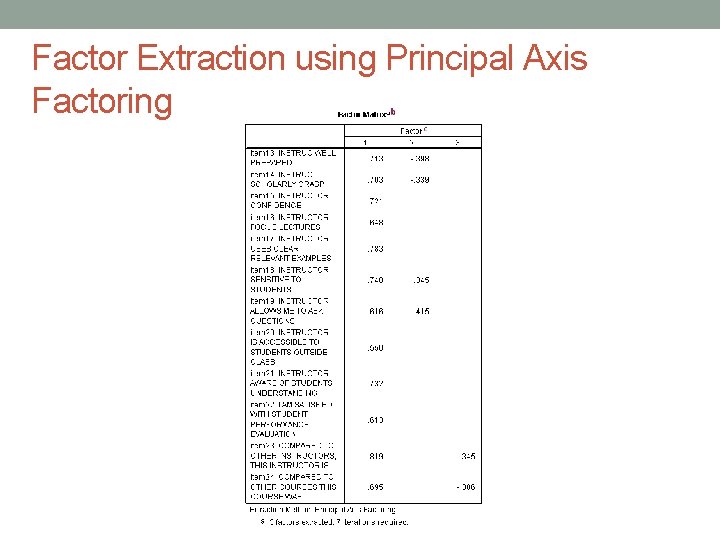
Factor Extraction using Principal Axis Factoring

Factor Rotation Unrotated factors are typically not very interpretable (most factors are correlated with may variables). Factors are rotated to make them more meaningful and easier to interpret (each variable is associated with a minimal number of factors). Different rotation methods may result in the identification of somewhat different factors.

Factor Rotation Two types of rotation o Orthogonal – produces uncorrelated factors/components § Varimax: most popular • attempts to minimize the number of variables that have high loadings on a factor. • enhances the interpretability of the factors § Quartimax § Equamax o Oblique – produces correlated factors/components § used less frequently because results are more difficult to summarize § types • Direct Quartimin • Promax • Harris-Kaiser Orthoblique

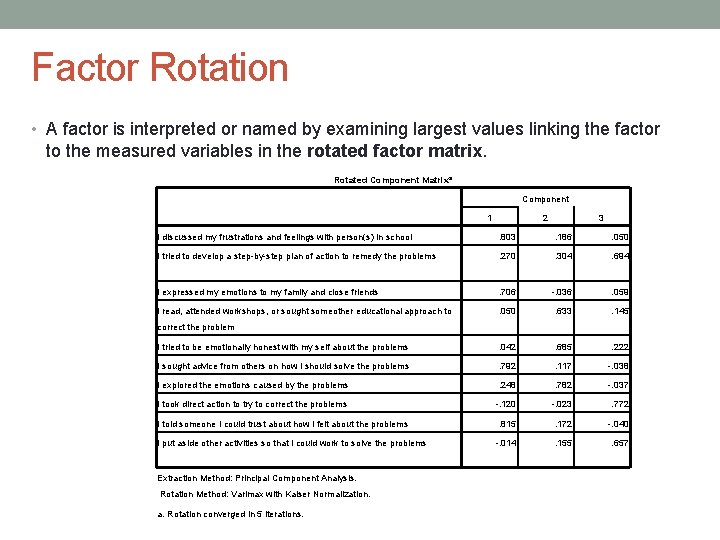
Factor Rotation • A factor is interpreted or named by examining largest values linking the factor to the measured variables in the rotated factor matrix. Rotated Component Matrixa Component 1 2 3 I discussed my frustrations and feelings with person(s) in school . 803 . 186 . 050 I tried to develop a step-by-step plan of action to remedy the problems . 270 . 304 . 694 I expressed my emotions to my family and close friends . 706 -. 036 . 059 I read, attended workshops, or sought someother educational approach to . 050 . 633 . 145 I tried to be emotionally honest with my self about the problems . 042 . 685 . 222 I sought advice from others on how I should solve the problems . 792 . 117 -. 038 I explored the emotions caused by the problems . 248 . 782 -. 037 I took direct action to try to correct the problems -. 120 -. 023 . 772 . 815 . 172 -. 040 -. 014 . 155 . 657 correct the problem I told someone I could trust about how I felt about the problems I put aside other activities so that I could work to solve the problems Extraction Method: Principal Component Analysis. Rotation Method: Varimax with Kaiser Normalization. a. Rotation converged in 5 iterations.

Making Final Decisions • Making final decisions o should base final decision on number of factors for rotated solution that is most interpretable. o identify factors by grouping variables that have large loadings for same factor o interpret factors according to meaning of the variables o decision should be guided by: § conceptual beliefs about the number of factors from past research or theory § Eigenvalues computed earlier § relative interpretability of rotated solutions computed