From PCA to Confirmatory FA from using Stata



![http: //lib. stat. cmu. edu/DASL/Datafiles/Colleges. html data=read. table("G: /Albert/COURSES/RMMSS/Schools 1. txt", header=T) names(data) [1] http: //lib. stat. cmu. edu/DASL/Datafiles/Colleges. html data=read. table("G: /Albert/COURSES/RMMSS/Schools 1. txt", header=T) names(data) [1]](https://slidetodoc.com/presentation_image_h/f7f2afe8f363d11088d0fa35b98c1cbc/image-5.jpg)

![. graph f 2 f 1, s([_n]) . graph f 2 f 1, s([_n])](https://slidetodoc.com/presentation_image_h/f7f2afe8f363d11088d0fa35b98c1cbc/image-10.jpg)


![> data[, 1] [1] Amherst Swarthmore [6] Pomona Wesleyan Williams Smith Davidson Clar. Mc. > data[, 1] [1] Amherst Swarthmore [6] Pomona Wesleyan Williams Smith Davidson Clar. Mc.](https://slidetodoc.com/presentation_image_h/f7f2afe8f363d11088d0fa35b98c1cbc/image-13.jpg)
![DD=dist(pca$scores[, 1: 2], method ="euclidean", diag=FALSE) clust=hclust(DD, method="complete", members=NULL) plot(clust, labels=data[, 1], cex=. 8, DD=dist(pca$scores[, 1: 2], method ="euclidean", diag=FALSE) clust=hclust(DD, method="complete", members=NULL) plot(clust, labels=data[, 1], cex=. 8,](https://slidetodoc.com/presentation_image_h/f7f2afe8f363d11088d0fa35b98c1cbc/image-14.jpg)

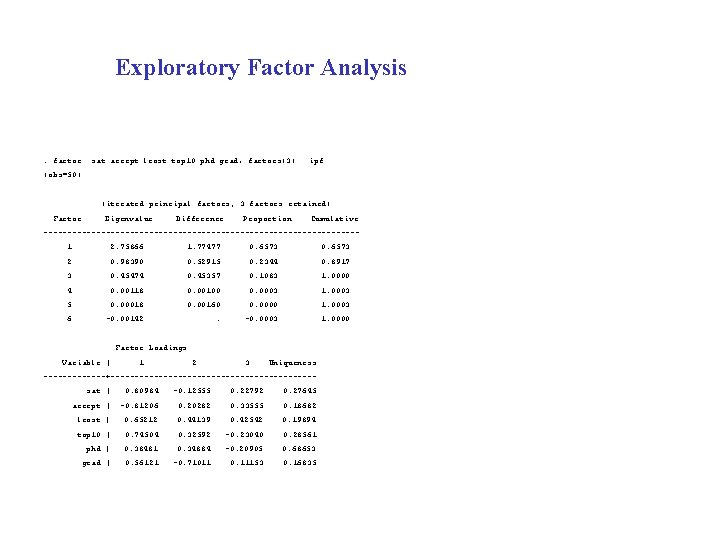




![data=read. table("E: /Albert/COURSES/RMMSS/ Mx/ADOPTION. txt", header=T) names(data) [1] "ADOPt 1" "ADOPt 2" "VALUE data=read. table("E: /Albert/COURSES/RMMSS/ Mx/ADOPTION. txt", header=T) names(data) [1] "ADOPt 1" "ADOPt 2" "VALUE](https://slidetodoc.com/presentation_image_h/f7f2afe8f363d11088d0fa35b98c1cbc/image-21.jpg)

![Exploratory Factor Analysis, ML method > data=read. table("E: /Albert/COURSES/RMMSS/Mx/ADOPTION. txt", header=T) > names(data) [1] Exploratory Factor Analysis, ML method > data=read. table("E: /Albert/COURSES/RMMSS/Mx/ADOPTION. txt", header=T) > names(data) [1]](https://slidetodoc.com/presentation_image_h/f7f2afe8f363d11088d0fa35b98c1cbc/image-23.jpg)








- Slides: 35

From PCA to Confirmatory FA (from using Stata to using Mx and other SEM software) References: Chapter 8 of Hamilton Chapter 10 of Lattin et al Data sets: College. txt, Govern. sav, Adoption. txt

Class 1 • Principal Components • Exploratory Factor Model • Confirmatory Factor Model

Principal Components Basic principles and the use of the method, with an example Chapter 8 of Hamilton, pp. 249 -267

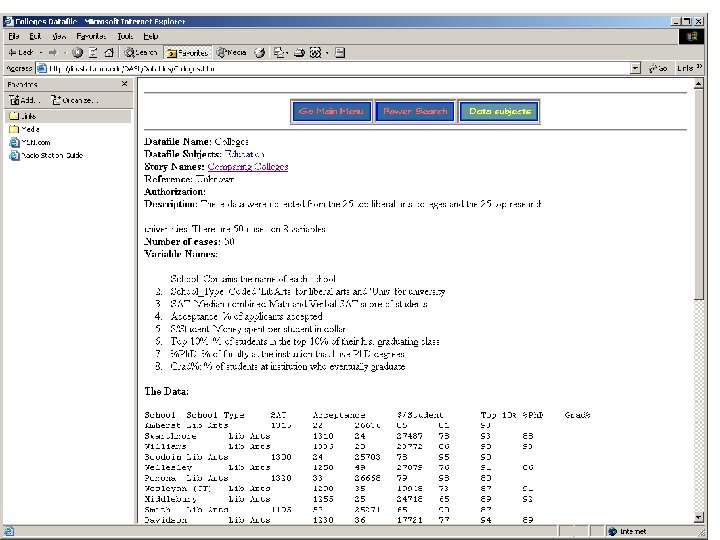
![http lib stat cmu eduDASLDatafilesColleges html dataread tableG AlbertCOURSESRMMSSSchools 1 txt headerT namesdata 1 http: //lib. stat. cmu. edu/DASL/Datafiles/Colleges. html data=read. table("G: /Albert/COURSES/RMMSS/Schools 1. txt", header=T) names(data) [1]](https://slidetodoc.com/presentation_image_h/f7f2afe8f363d11088d0fa35b98c1cbc/image-5.jpg)
http: //lib. stat. cmu. edu/DASL/Datafiles/Colleges. html data=read. table("G: /Albert/COURSES/RMMSS/Schools 1. txt", header=T) names(data) [1] "School" "School. T" "SAT" "Accept" "Cost. St" "Top 10" "Ph. D" [8] "Grad" attach(data) pairs(data[, 3: 8]) l. Cost=log(Cost. St) cdata=cbind(data[, 3: 4], l. Cost, data[, 6: 8]) pairs(cdata)

Principal Components Analysis (PCA) Yj = aj 1 PC 1 + aj 2 PC 2 + Ej, j = 1, 2, . . . P the Yj are manifest variables Ej = aj 3 PC 3 +. . ajp PCp the PC are called principal components Let Rj 2 the R 2 of the (linear) regression of Yj on PC 1 and PC 2 In PCA, the a’s are choosen so to maximize sumj Rj 2

use "G: AlbertCOURSESRMMSSschool 1. dta", clear. edit - preserve. summarize sat accept costst top 10 phd grad Variable | Obs Mean Std. Dev. Min Max -------+---------------------------- sat | 50 1263. 96 62. 32959 1109 1400 accept | 50 37. 84 13. 36361 17 67 costst | 50 30247. 2 15266. 17 17520 102262 top 10 | 50 74. 44 13. 51516 47 98 phd | 50 90. 56 8. 258972 58 100 -------+---------------------------- grad | 50 83. 48 7. 557237 61 95 .

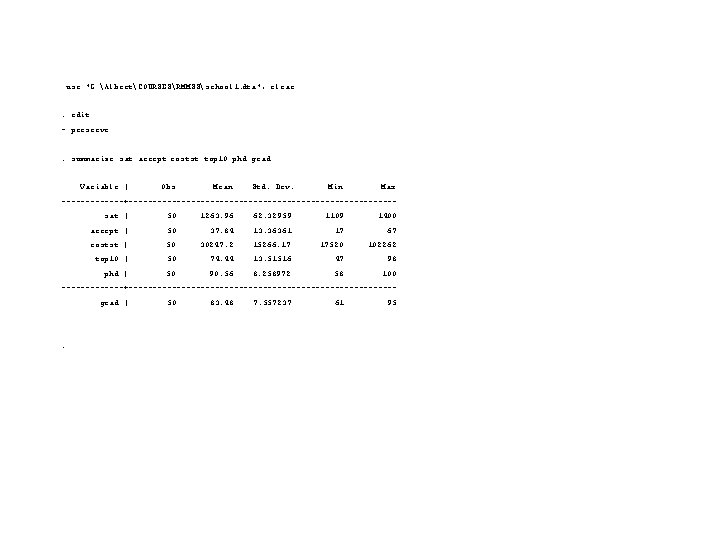
. Normalized pc . gen lcost = log(costst). pca sat accept lcost top 10 phd grad, factors(2) (obs=50) (principal components; 2 components retained) Component Eigenvalue Difference Proportion Cumulative --------------------------------- 1 3. 01940 1. 74300 0. 5032 2 1. 27640 0. 52532 0. 2127 0. 7160 3 0. 75108 0. 25948 0. 1252 0. 8411 4 0. 49160 0. 25118 0. 0819 0. 9231 5 0. 24042 0. 01930 0. 0401 0. 9631 6 0. 22112 . 0. 0369 1. 0000 Eigenvectors Variable | 1 2 -------+---------- sat | 0. 48705 -0. 20272 accept | -0. 47435 0. 20082 lcost | 0. 38708 0. 30674 top 10 | 0. 45710 0. 28373 phd | 0. 27982 0. 55460 grad | 0. 31732 -0. 66060. greigen . summarize f 1 f 2 . score f 1 f 2 Variable | Obs Mean Std. Dev. Min Max (based on unrotated principal components) -------+---------------------------- Scoring Coefficients f 1 | 50 2. 76 e-09 1. 737641 -2. 693964 3. 290203 Variable | 1 2 f 2 | 50 -7. 38 e-09 1. 129777 -2. 067842 3. 50152 -------+---------- sat | 0. 48705 -0. 20272 accept | -0. 47435 0. 20082

![graph f 2 f 1 sn . graph f 2 f 1, s([_n])](https://slidetodoc.com/presentation_image_h/f7f2afe8f363d11088d0fa35b98c1cbc/image-10.jpg)
. graph f 2 f 1, s([_n])

. cor sat accept lcost top 10 phd grad f 1 f 2 (obs=50) | sat accept lcost top 10 phd grad f 1 f 2 -------+------------------------------------ sat | 1. 0000 accept | -0. 6068 1. 0000 lcost | 0. 5697 -0. 2972 1. 0000 top 10 | 0. 5093 -0. 6163 0. 5321 1. 0000 phd | 0. 2209 -0. 3117 0. 3155 0. 4486 1. 0000 grad | 0. 5691 -0. 5622 0. 0999 0. 1613 -0. 0554 1. 0000 f 1 | 0. 8463 -0. 8243 0. 6726 0. 7943 0. 4862 0. 5514 1. 0000 f 2 | -0. 2290 0. 2269 0. 3465 0. 3206 0. 6266 -0. 7463 -0. 0000 1. 0000

library(mva) help('factanal') help('princomp') pca=princomp(cdata, cor=T, scores=T) biplot(pca) > summary(pca) Importance of components: Comp. 1 Comp. 2 Comp. 3 Comp. 4 Comp. 5 Standard deviation 1. 7376411 1. 1297771 0. 8666462 0. 70114124 0. 49032369 Proportion of Variance 0. 5032328 0. 2127327 0. 1251793 0. 08193317 0. 04006955 Cumulative Proportion 0. 5032328 0. 7159655 0. 8411447 0. 92307790 0. 96314745 round(cov(pca$scores[, 1: 2]), 3) Comp. 1 Comp. 2 Comp. 1 3. 081 0. 000 Comp. 2 0. 000 1. 302
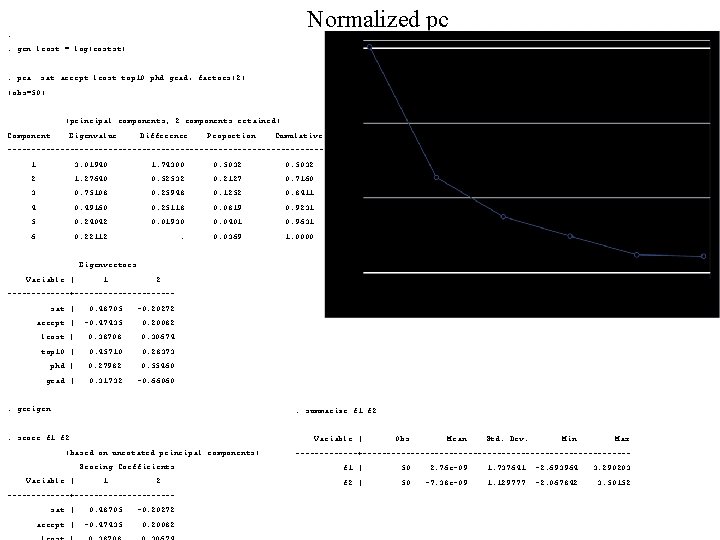
![data 1 1 Amherst Swarthmore 6 Pomona Wesleyan Williams Smith Davidson Clar Mc > data[, 1] [1] Amherst Swarthmore [6] Pomona Wesleyan Williams Smith Davidson Clar. Mc.](https://slidetodoc.com/presentation_image_h/f7f2afe8f363d11088d0fa35b98c1cbc/image-13.jpg)
> data[, 1] [1] Amherst Swarthmore [6] Pomona Wesleyan Williams Smith Davidson Clar. Mc. Kenna Oberlin Washington. Lee Carleton [16] Grinnell Mount. Holyoke Colby Colgate [26] Harvard [31] MIT Stanford Duke [36] Uof. Chicago [41] Rice [46] UMichican Brown UCLA Wellesley Middlebury [11] Vassar [21] Haverford Bowdoin Bryn. Mawr Yale Dartmouth UPenn UVa. Hamilton Bates Occidental Barnard Princeton Cornell Berkeley Georgetown Cal. Tech Columbia Johns. Hopkins UNC Carnegie. Mellon Northwestern Washington. U Uof. Rochester
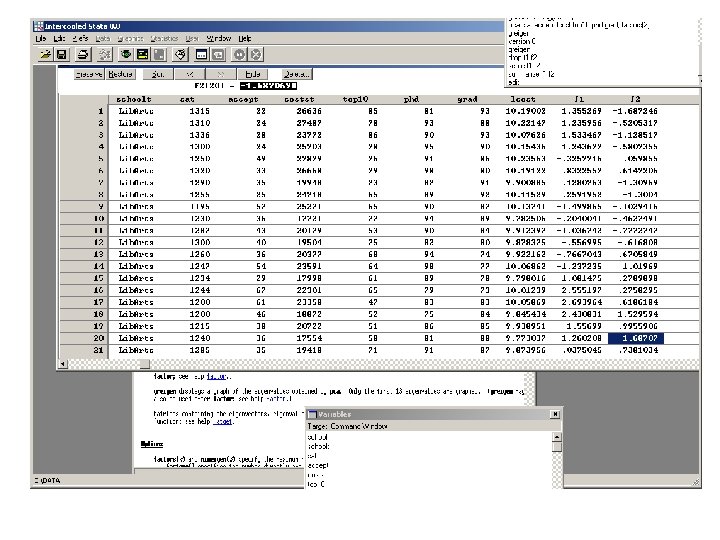
![DDdistpcascores 1 2 method euclidean diagFALSE clusthclustDD methodcomplete membersNULL plotclust labelsdata 1 cex 8 DD=dist(pca$scores[, 1: 2], method ="euclidean", diag=FALSE) clust=hclust(DD, method="complete", members=NULL) plot(clust, labels=data[, 1], cex=. 8,](https://slidetodoc.com/presentation_image_h/f7f2afe8f363d11088d0fa35b98c1cbc/image-14.jpg)
DD=dist(pca$scores[, 1: 2], method ="euclidean", diag=FALSE) clust=hclust(DD, method="complete", members=NULL) plot(clust, labels=data[, 1], cex=. 8, col="blue", main="clustering of education")

Chapter 8 of Hamilton, pp. 270 -281 (Exploratory) Factor Analysis Yj = aj 1 F 1 + aj 2 F 2 + Ej, j = 1, 2, . . . P Ej =. . uncorrelated across j !! The a’s are choosen by principal factor method, ML, . . . There is no unique solution (model is non-identified). Rotation methods to maximize interpretation (e. g. , Varimax).

Exploratory Factor Analysis . factor sat accept lcost top 10 phd grad, factors(3) ipf (obs=50) (iterated principal factors; 3 factors retained) Factor Eigenvalue Difference Proportion Cumulative --------------------------------- 1 2. 75866 1. 77477 0. 6573 2 0. 98390 0. 52915 0. 2344 0. 8917 3 0. 45474 0. 45357 0. 1083 1. 0000 4 0. 00118 0. 00100 0. 0003 1. 0003 5 0. 00018 0. 00160 0. 0000 1. 0003 6 -0. 00142 . -0. 0003 1. 0000 Factor Loadings Variable | 1 2 3 Uniqueness -------+--------------------- sat | 0. 80984 -0. 12555 0. 22792 0. 27645 accept | -0. 81206 0. 20282 0. 33555 0. 18682 lcost | 0. 65212 0. 44139 0. 42542 0. 19894 top 10 | 0. 74504 0. 32592 -0. 23040 0. 28561 phd | 0. 38481 0. 34884 -0. 20905 0. 68653 grad | 0. 56121 -0. 71011 0. 11153 0. 16835

Exploratory Factor Analysis > factanal(cdata, factors=2) > summary(fac) Call: Length Class Mode fac=factanal(cdata, factors=2, scores="regression") converged 1 -none- logical loadings 12 loadings numeric Uniquenesses: uniquenesses 6 -none- numeric SAT Accept l. Cost Top 10 Ph. D Grad correlation 36 -none- numeric 0. 388 0. 353 0. 600 0. 256 0. 708 0. 005 criteria 3 -none- numeric factors 1 -none- numeric Loadings: dof 1 -none- numeric Factor 1 Factor 2 method 1 -none- character SAT 0. 484 0. 615 scores 100 -none- numeric Accept -0. 523 -0. 612 STATISTIC 1 -none- numeric l. Cost 0. 613 0. 155 PVAL 1 -none- numeric Top 10 0. 830 0. 235 n. obs 1 -none- numeric Ph. D 0. 540 call 4 -none- call Grad 0. 994 > Factor 1 Factor 2 SS loadings 1. 871 1. 819 Proportion Var 0. 312 0. 303 Cumulative Var 0. 312 0. 615 Test of the hypothesis that 2 factors are sufficient. The chi square statistic is 11. 47 on 4 degrees of freedom. The p-value is 0. 0217 >

(Confirmatory) Factor Analysis Yj = aj 1 F 1 + aj 2 F 2 + Ej, j = 1, 2, . . . P Ej =. . uncorrelated across j !! Some of the a’s are free, other restricted a priori (to 0 s, 1 s, or by equality among them), estimation method is ML, GLS, . . . There is uniqueness in the solution (an identified model).

Lattin and Roberts data of adoption new technologies p. 366 of Lattin et al. See the data file adoption. txt in RMMRS

Analysis of Adoption data
![dataread tableE AlbertCOURSESRMMSS MxADOPTION txt headerT namesdata 1 ADOPt 1 ADOPt 2 VALUE data=read. table("E: /Albert/COURSES/RMMSS/ Mx/ADOPTION. txt", header=T) names(data) [1] "ADOPt 1" "ADOPt 2" "VALUE](https://slidetodoc.com/presentation_image_h/f7f2afe8f363d11088d0fa35b98c1cbc/image-21.jpg)
data=read. table("E: /Albert/COURSES/RMMSS/ Mx/ADOPTION. txt", header=T) names(data) [1] "ADOPt 1" "ADOPt 2" "VALUE 1" "VALUE 2" "VALUE 3" "USAGE 1" "USAGE 2" "USAGE 3" attach(data) round(cov(data, use="complete. obs"), 2) ADOPt 1 ADOPt 2 VALUE 1 VALUE 2 VALUE 3 USAGE 1 USAGE 2 USAGE 3 ADOPt 1 675. 17 489. 24 6. 25 5. 46 4. 08 10. 62 11. 69 7. 12 ADOPt 2 489. 24 994. 31 4. 16 4. 46 3. 42 16. 35 17. 92 12. 17 VALUE 1 6. 25 4. 16 0. 95 0. 37 0. 45 0. 16 0. 19 0. 12 VALUE 2 5. 46 4. 46 0. 37 0. 83 0. 31 0. 12 0. 07 VALUE 3 4. 08 3. 42 0. 45 0. 31 0. 86 0. 13 0. 18 0. 05 USAGE 1 10. 62 16. 35 0. 16 0. 11 0. 13 0. 76 0. 64 0. 45 USAGE 2 11. 69 17. 92 0. 19 0. 12 0. 18 0. 64 0. 92 0. 55 USAGE 3 7. 12 12. 17 0. 12 0. 07 0. 05 0. 45 0. 55 0. 64 dim(data) [1] 188 8

Adoption. dat Data Nimput=8 Nobservations=188 CMatrix 675. 17 489. 24 994. 31 6. 25 4. 16 0. 95 5. 46 4. 46 0. 37 0. 83 4. 08 3. 42 0. 45 0. 31 0. 86 10. 62 16. 35 0. 16 0. 11 0. 13 0. 76 11. 69 17. 92 0. 19 0. 12 0. 18 0. 64 0. 92 7. 12 12. 17 0. 12 0. 07 0. 05 0. 45 0. 55 0. 64 Labels ADOPt 1 ADOPt 2 VALUE 1 VALUE 2 VALUE 3 USAGE 1 USAGE 2 USAGE 3
![Exploratory Factor Analysis ML method dataread tableE AlbertCOURSESRMMSSMxADOPTION txt headerT namesdata 1 Exploratory Factor Analysis, ML method > data=read. table("E: /Albert/COURSES/RMMSS/Mx/ADOPTION. txt", header=T) > names(data) [1]](https://slidetodoc.com/presentation_image_h/f7f2afe8f363d11088d0fa35b98c1cbc/image-23.jpg)
Exploratory Factor Analysis, ML method > data=read. table("E: /Albert/COURSES/RMMSS/Mx/ADOPTION. txt", header=T) > names(data) [1] "ADOPt 1" "ADOPt 2" "VALUE 1" "VALUE 2" "VALUE 3" "USAGE 1" "USAGE 2" "USAGE 3" attach(data) factanal(cbind(VALUE 1, VALUE 2, VALUE 3, USAGE 1, USAGE 2, USAGE 3), factors=2, rotation="varimax") Call: factanal(x = cbind(VALUE 1, VALUE 2, VALUE 3, USAGE 1, USAGE 2, USAGE 3), factors = 2) Uniquenesses: VALUE 1 VALUE 2 VALUE 3 USAGE 1 USAGE 2 USAGE 3 0. 493 0. 648 0. 484 0. 291 0. 165 0. 292 Loadings: Factor 1 Factor 2 VALUE 1 0. 127 0. 700 VALUE 2 0. 586 VALUE 3 0. 714 USAGE 1 0. 823 0. 179 Test of the hypothesis that 2 factors are sufficient. USAGE 2 0. 896 0. 179 The chi square statistic is 1. 82 on 4 degrees of freedom. USAGE 3 0. 836 The p-value is 0. 768 Factor 1 Factor 2 SS loadings 2. 209 1. 418 Proportion Var 0. 368 0. 236 Cumulative Var 0. 368 0. 604

Adoption. dat Data Nimput=8 Nobservations=188 CMatrix 675. 17 489. 24 994. 31 6. 25 4. 16 0. 95 5. 46 4. 46 0. 37 0. 83 4. 08 3. 42 0. 45 0. 31 0. 86 10. 62 16. 35 0. 16 0. 11 0. 13 0. 76 11. 69 17. 92 0. 19 0. 12 0. 18 0. 64 0. 92 7. 12 12. 17 0. 12 0. 07 0. 05 0. 45 0. 55 0. 64 Labels ADOPt 1 ADOPt 2 VALUE 1 VALUE 2 VALUE 3 USAGE 1 USAGE 2 USAGE 3

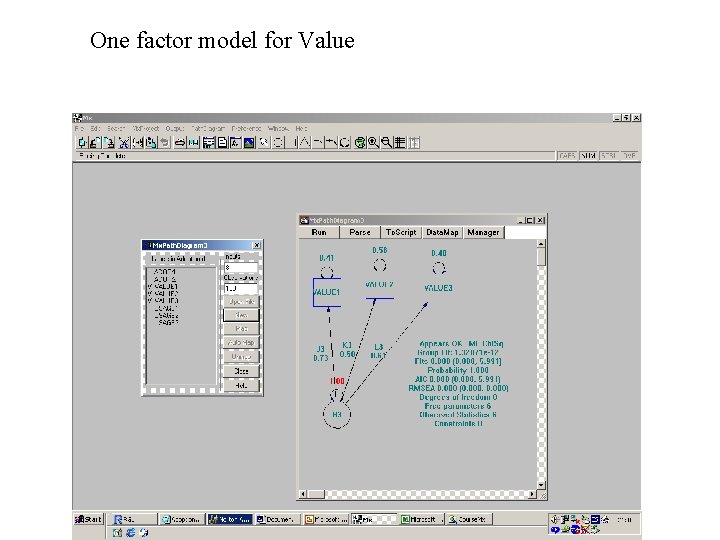
One factor model for Value

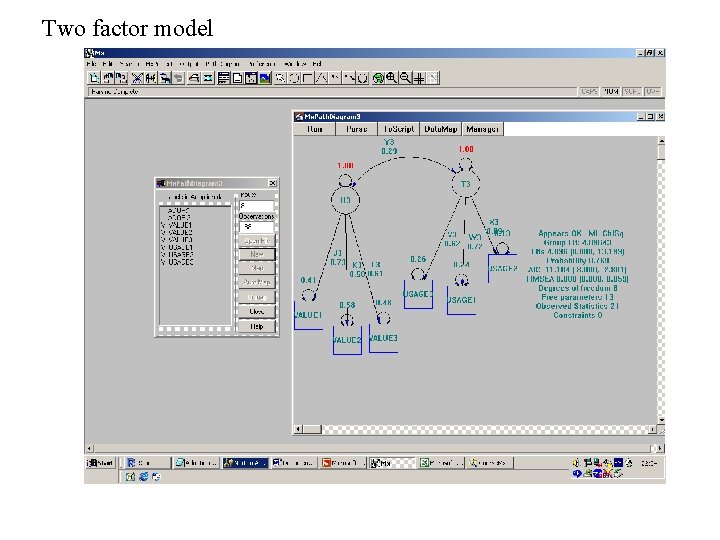
Two factor model

Factor Analysis Charles Spearman, 1904 Acording to the two-factor theory of intelligence, the performance of any intellectual act requires some combination of "g", which is available to the same individual to the same degree for all intellectual acts, and of "specific factors" or "s" which are specific to that act and which varies in strength from one act to another. If one knows how a person performs on one task that is highly saturated with "g", one can safely predict a similar level of performance for a another highly "g" saturated task. Prediction of performance on tasks with high "s" factors are less accurate. Nevertheless, since "g" pervades all tasks, prediction will be significantly better than chance. Thus, the most important information to have about a person's intellectual ability is an estimate of their "g".

Spearman, 1904 Variables Correlation matrix CLASSIC FRENCH ENGLISH MATH DISCRIM MUSIC = = = V 1 V 2 V 3 V 4 V 5 V 6 1. 83 1. 78. 67 1. 70. 64 1. 66. 65. 54. 45 1. 63. 57. 51. 40 1 cases = 23;

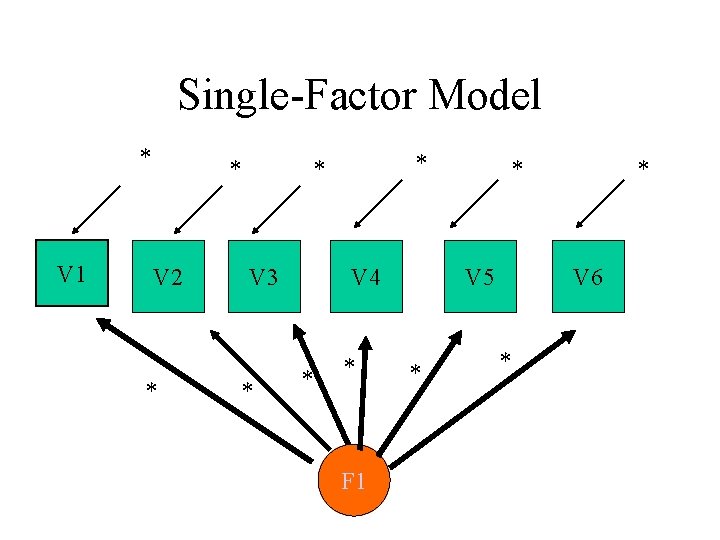
Single-Factor Model * V 1 * V 2 * * * V 3 * V 4 * * F 1 * V 5 * * V 6 *

EQS code for a factor model

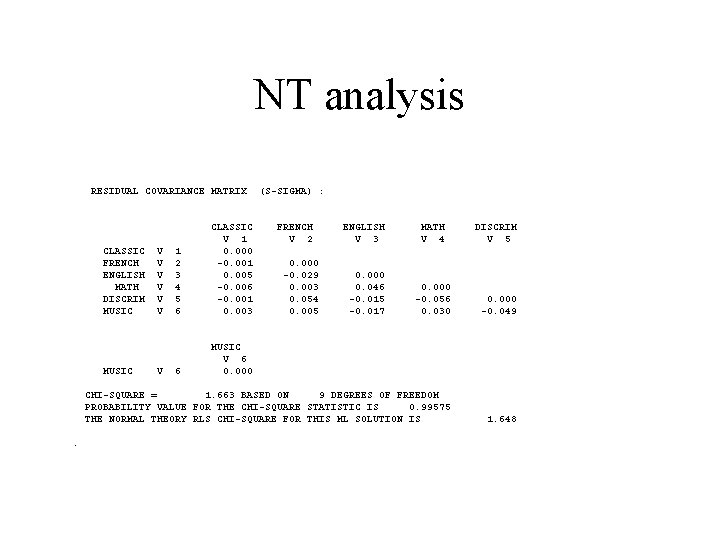
NT analysis RESIDUAL COVARIANCE MATRIX ENGLISH V 3 MATH V 4 DISCRIM V 5 0. 000 0. 046 -0. 015 -0. 017 0. 000 -0. 056 0. 030 0. 000 -0. 049 CHI-SQUARE = 1. 663 BASED ON 9 DEGREES OF FREEDOM PROBABILITY VALUE FOR THE CHI-SQUARE STATISTIC IS 0. 99575 THE NORMAL THEORY RLS CHI-SQUARE FOR THIS ML SOLUTION IS 1. 648 CLASSIC FRENCH ENGLISH MATH DISCRIM MUSIC . V V V V 1 2 3 4 5 6 CLASSIC V 1 0. 000 -0. 001 0. 005 -0. 006 -0. 001 0. 003 6 MUSIC V 6 0. 000 (S-SIGMA) : FRENCH V 2 0. 000 -0. 029 0. 003 0. 054 0. 005

Loadings’ estimates, s. e. and z-test statistics CLASSIC =V 1 = . 960*F 1 +1. 000 E 1 . 160 6. 019 FRENCH =V 2 = . 866*F 1 +1. 000 E 2 . 171 5. 049 ENGLISH =V 3 = . 807*F 1 +1. 000 E 3 . 178 4. 529 MATH =V 4 = . 736*F 1 +1. 000 E 4 . 186 3. 964 DISCRIM =V 5 = . 688*F 1 +1. 000 E 5 . 190 3. 621 MUSIC =V 6 = . 653*F 1 +1. 000 E 6 . 193 3. 382

Estimates of unique-factors E 1 -CLASSIC . 078*I . 064 I 1. 224 I E 2 -FRENCH . 251*I . 093 I 2. 695 I I E 3 -ENGLISH . 349*I . 118 I 2. 958 I I E 4 - MATH . 459*I . 148 I 3. 100 I I E 5 -DISCRIM . 527*I . 167 I 3. 155 I E 6 -MUSIC . 574*I . 180 I 3. 184 I I

STANDARDIZED SOLUTION: CLASSIC FRENCH ENGLISH MATH DISCRIM MUSIC =V 1 =V 2 =V 3 =V 4 =V 5 =V 6 = = = . 960*F 1. 866*F 1. 807*F 1. 736*F 1. 688*F 1. 653*F 1 + + + . 279. 501. 591. 677. 726. 758 E 1 E 2 E 3 E 4 E 5 E 6

Data of Lawley and Maxwell M 0: /TITLE Lawley and Maxwell data /SPECIFICATIONS CAS=220; VAR=6; ME=ML; /LABEL v 1 =Gaelic; v 2 = English; v 3 = Histo; v 4 =aritm; /EQUATIONS v 5 =Algebra; V 1= *F 1 + E 1; v 6 =Geometry; V 2= *F 1 + E 2; /EQUATIONS V 3= *F 1 + E 3; V 1= *F 1 + E 1; V 4= *F 2 + E 4; V 5= *F 2 + E 5; V 2= *F 1 + E 2; V 6= *F 2 + E 6; V 3= *F 1 + E 3; /VARIANCES V 4= *F 1 + E 4; F 1 = 1; F 2=1; E 1 TO E 6 = *; V 5= *F 1 + E 5; /COVARIANCES V 6= *F 1 + E 6; /VARIANCES F 1, F 2 = *; F 1 = 1; E 1 TO E 6 = *; /COVARIANCES /MATRIX 1. 439. 410. 288. 329. 248. 439 1. 354. 320. 329. 410. 351 1. 164. 190. 181. 288. 354. 164 1. 595. 470. 329. 320. 190. 595 1. 464. 248. 329. 181. 470. 464 1 /END M 1: M 0, Single factor model CHI-SQUARE = 52. 841, 9 df P-value LESS THAN 0. 001 GAELIC =V 1 = . 687*F 1 + 1. 000 E 1 . 076 9. 079 ENGLISH =V 2 = . 672*F 1 + 1. 000 E 2 . 076 8. 896 HISTO =V 3 = . 533*F 1 + 1. 000 E 3 . 076 7. 047 ARITM =V 4 = . 766*F 2 + 1. 000 E 4 . 067 11. 379 ALGEBRA =V 5 = . 768*F 2 + 1. 000 E 5 . 067 11. 411 GEOMETRY=V 6 = . 616*F 2 + 1. 000 E 6 . 069 8. 942 COVARIANCES AMONG INDEPENDENT VARIABLES ------------------- I F 2 - F 2 . 597*I I F 1 - F 1 . 072 I 8. 308 M 1, Two factor model with correlated factors : CHI-SQUARE = 7. 953, 8 df P-value = 0. 43804