6 Principal Component Analysis Principal component analysis PCA


























- Slides: 40

6. Principal Component Analysis Principal component analysis (PCA) is a technique that is useful for the compression and classification of data. The purpose is to reduce the dimensionality of a data set (sample) by finding a new set of variables, smaller than the original set, that nonetheless retains most of the sample's information. 1 er. Escuela Red Pro. TIC - Tandil, 18 -28 de Abril, 2006

6. Principal Component Analysis By information we mean the variation present in the sample, given by the correlations between the original variables. The new variables, called principal components (PCs), are uncorrelated, and are ordered by the fraction of the total information each retains. 1 er. Escuela Red Pro. TIC - Tandil, 18 -28 de Abril, 2006

6. Principal Component Analysis Principal component • direction of maximum variance in the input space • principal eigenvector of the covariance matrix Goal: Relate these two definitions 1 er. Escuela Red Pro. TIC - Tandil, 18 -28 de Abril, 2006

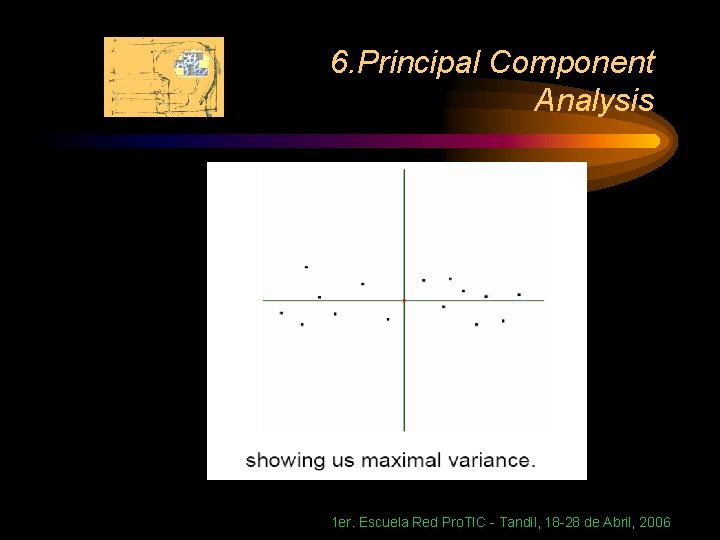
6. Principal Component Analysis • Variance A random variable fluctuating about its mean value Average of the square of the fluctuations 1 er. Escuela Red Pro. TIC - Tandil, 18 -28 de Abril, 2006

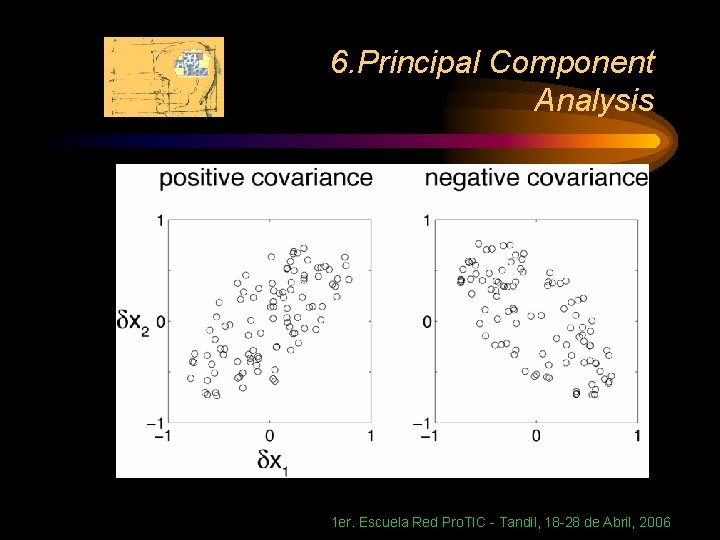
6. Principal Component Analysis • Covariance Pair of random variables, each fluctuating about its mean value. Average of product of fluctuations 1 er. Escuela Red Pro. TIC - Tandil, 18 -28 de Abril, 2006

6. Principal Component Analysis 1 er. Escuela Red Pro. TIC - Tandil, 18 -28 de Abril, 2006

6. Principal Component Analysis • Covariance matrix N random variables Nx. N symmetric matrix Diagonal elements are variances 1 er. Escuela Red Pro. TIC - Tandil, 18 -28 de Abril, 2006

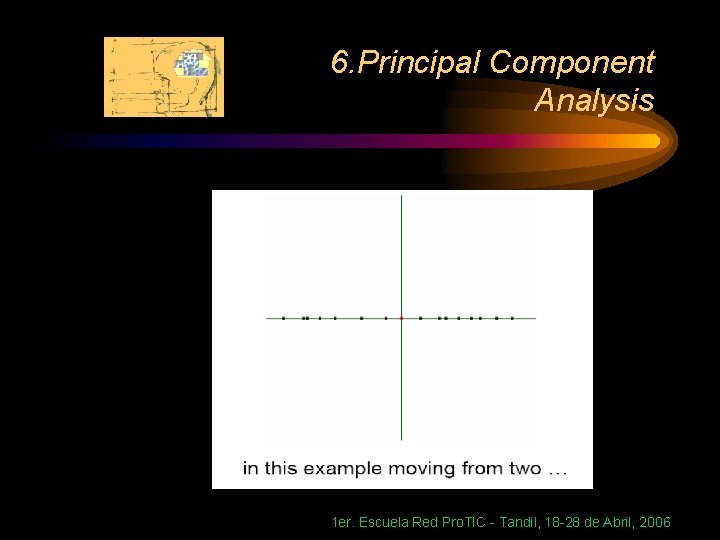
6. Principal Component Analysis Principal components • eigenvectors with k largest eigenvalues Now you can calculate them, but what do they mean? 1 er. Escuela Red Pro. TIC - Tandil, 18 -28 de Abril, 2006

6. Principal Component Analysis • Covariance to variance From the covariance, the variance of any projection can be calculated. w : unit vector 1 er. Escuela Red Pro. TIC - Tandil, 18 -28 de Abril, 2006

6. Principal Component Analysis • Maximizing parallel variance Principal eigenvector of C (the one with the largest eigenvalue) 1 er. Escuela Red Pro. TIC - Tandil, 18 -28 de Abril, 2006

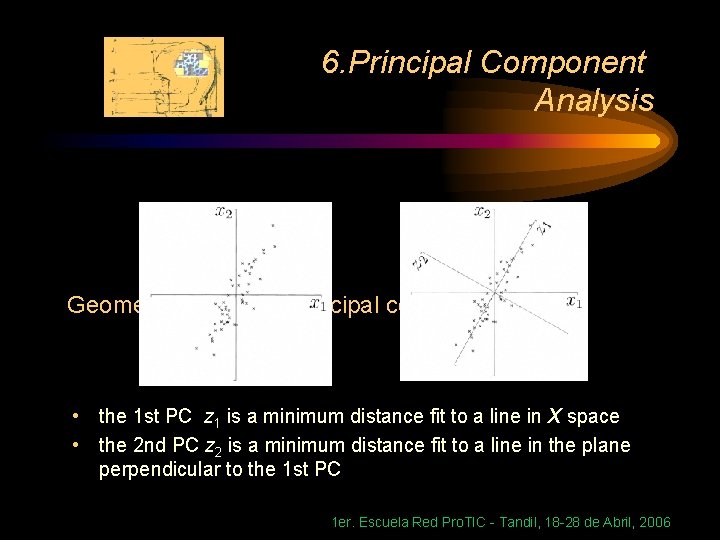
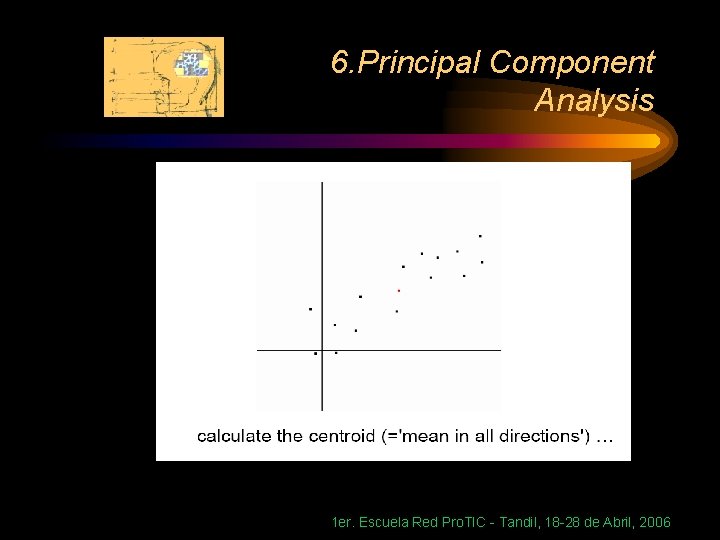
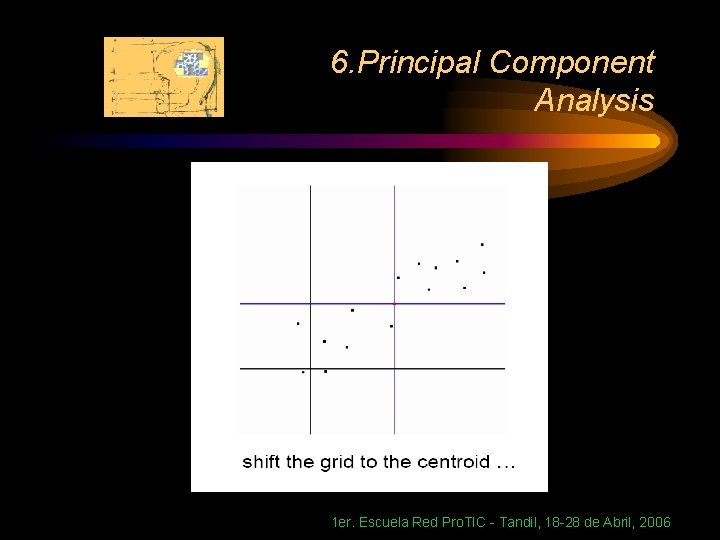
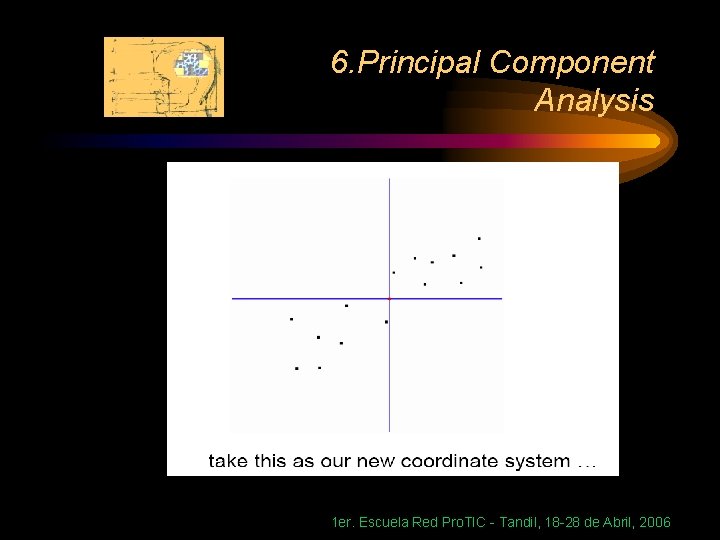
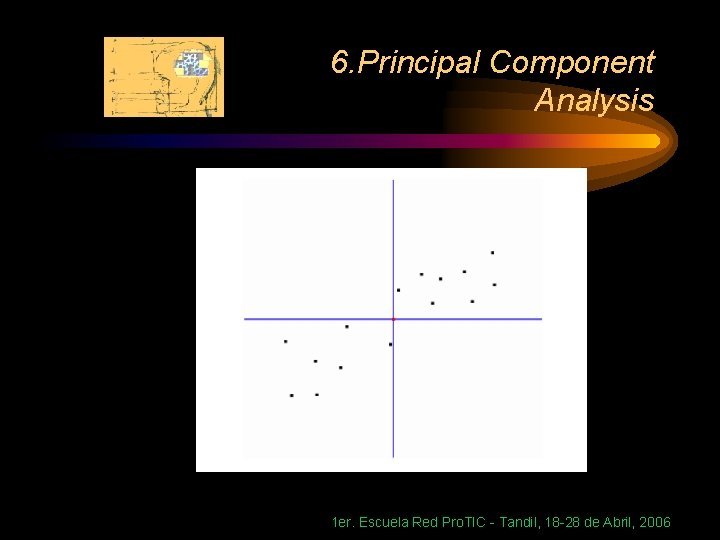
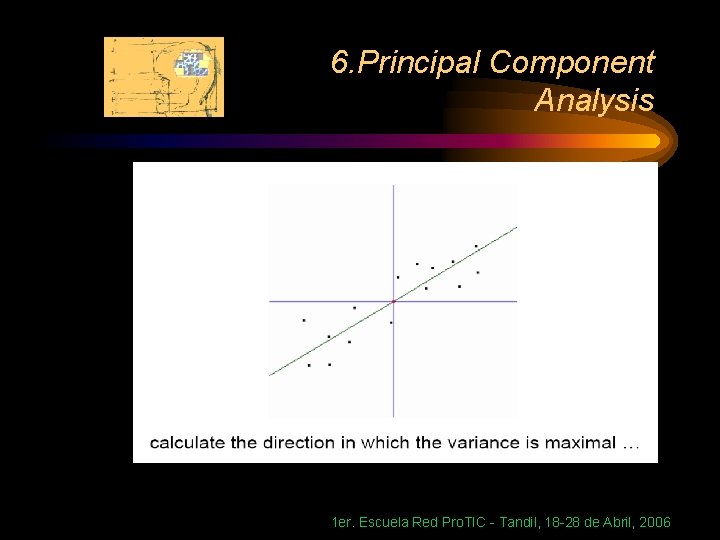
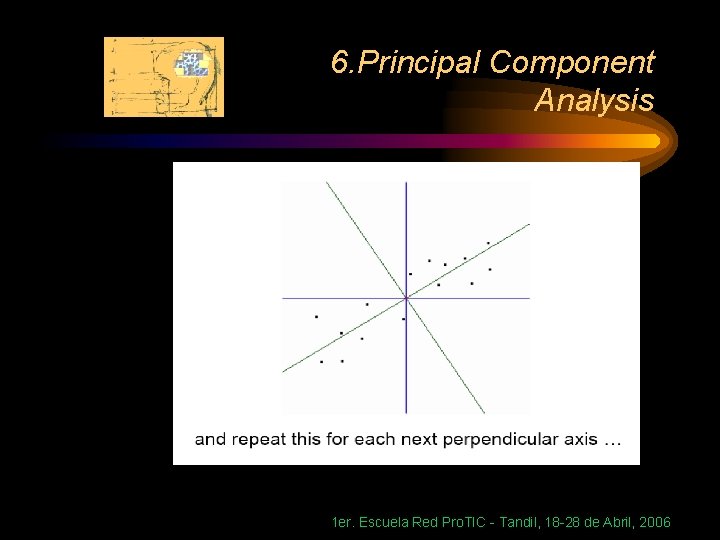
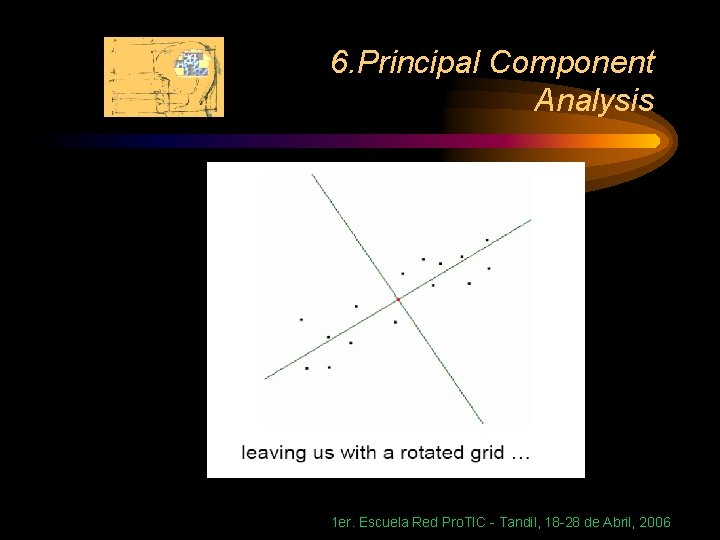
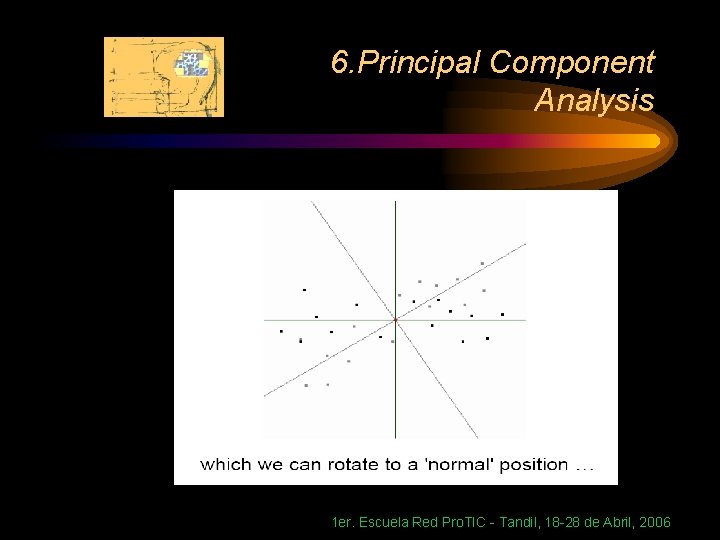
6. Principal Component Analysis Geometric picture of principal components • the 1 st PC z 1 is a minimum distance fit to a line in X space • the 2 nd PC z 2 is a minimum distance fit to a line in the plane perpendicular to the 1 st PC 1 er. Escuela Red Pro. TIC - Tandil, 18 -28 de Abril, 2006

6. Principal Component Analysis Then… 1 er. Escuela Red Pro. TIC - Tandil, 18 -28 de Abril, 2006

6. Principal Component Analysis 1 er. Escuela Red Pro. TIC - Tandil, 18 -28 de Abril, 2006

6. Principal Component Analysis 1 er. Escuela Red Pro. TIC - Tandil, 18 -28 de Abril, 2006

6. Principal Component Analysis 1 er. Escuela Red Pro. TIC - Tandil, 18 -28 de Abril, 2006

6. Principal Component Analysis 1 er. Escuela Red Pro. TIC - Tandil, 18 -28 de Abril, 2006

6. Principal Component Analysis 1 er. Escuela Red Pro. TIC - Tandil, 18 -28 de Abril, 2006

6. Principal Component Analysis 1 er. Escuela Red Pro. TIC - Tandil, 18 -28 de Abril, 2006

6. Principal Component Analysis 1 er. Escuela Red Pro. TIC - Tandil, 18 -28 de Abril, 2006

6. Principal Component Analysis 1 er. Escuela Red Pro. TIC - Tandil, 18 -28 de Abril, 2006

6. Principal Component Analysis 1 er. Escuela Red Pro. TIC - Tandil, 18 -28 de Abril, 2006

6. Principal Component Analysis 1 er. Escuela Red Pro. TIC - Tandil, 18 -28 de Abril, 2006

6. Principal Component Analysis 1 er. Escuela Red Pro. TIC - Tandil, 18 -28 de Abril, 2006

6. Principal Component Analysis 1 er. Escuela Red Pro. TIC - Tandil, 18 -28 de Abril, 2006

6. Principal Component Analysis 1 er. Escuela Red Pro. TIC - Tandil, 18 -28 de Abril, 2006

6. Principal Component Analysis 1 er. Escuela Red Pro. TIC - Tandil, 18 -28 de Abril, 2006

6. Principal Component Analysis Algebraic definition of PCs Given a sample of n observations on a vector of p λ variables x = (x 1, x 2, …. , xp) define the first principal component of the sample by the linear transformation where the vector is chosen such that is maximum 1 er. Escuela Red Pro. TIC - Tandil, 18 -28 de Abril, 2006

6. Principal Component Analysis Likewise, define the kth PC of the sample by the linear transformation where the vector is chosen such that is maximum subject to 1 er. Escuela Red Pro. TIC - Tandil, 18 -28 de Abril, 2006

6. Principal Component Analysis To find first note that is the covariance matrix for the variables 1 er. Escuela Red Pro. TIC - Tandil, 18 -28 de Abril, 2006

6. Principal Component Analysis To find maximize subject to Let λ be a Lagrange multiplier then maximize by differentiating… therefore is an eigenvector of corresponding to eigenvalue 1 er. Escuela Red Pro. TIC - Tandil, 18 -28 de Abril, 2006

6. Principal Component Analysis Algebraic derivation of We have maximized So is the largest eigenvalue of The first PC retains the greatest amount of variation in the sample. 1 er. Escuela Red Pro. TIC - Tandil, 18 -28 de Abril, 2006

6. Principal Component Analysis To find vector maximize subject to First note that then let λ and φ be Lagrange multipliers, and maximize 1 er. Escuela Red Pro. TIC - Tandil, 18 -28 de Abril, 2006

6. Principal Component Analysis We find that is also an eigenvector of whose eigenvalue is the second largest. In general The kth largest eigenvalue of the kth PC. is the variance of The kth PC retains the kth greatest fraction of the variation in the sample. 1 er. Escuela Red Pro. TIC - Tandil, 18 -28 de Abril, 2006

6. Principal Component Analysis Algebraic formulation of PCA Given a sample of n observations on a vector of p variables define a vector of p PCs according to where is an orthogonal p x p matrix whose kth column is the kth eigenvector of 1 er. Escuela Red Pro. TIC - Tandil, 18 -28 de Abril, 2006

6. Principal Component Analysis Then is the covariance matrix of the PCs, being diagonal with elements 1 er. Escuela Red Pro. TIC - Tandil, 18 -28 de Abril, 2006

6. Principal Component Analysis In general it is useful to define standardized variables by If the are each measured about their sample mean the covariance matrix correlation matrix of and the PCs of will be equal to the will be dimensionless 1 er. Escuela Red Pro. TIC - Tandil, 18 -28 de Abril, 2006

6. Principal Component Analysis Practical computation of PCs Given a sample of n observations on a vector of p variables (each measured about its sample mean) compute the covariance matrix where is the n x p matrix whose ith row is the ith observation 1 er. Escuela Red Pro. TIC - Tandil, 18 -28 de Abril, 2006

6. Principal Component Analysis Then, compute the n x p matrix whose ith row is the PC score for the ith observation: Write into PCs: to decompose each observation 1 er. Escuela Red Pro. TIC - Tandil, 18 -28 de Abril, 2006

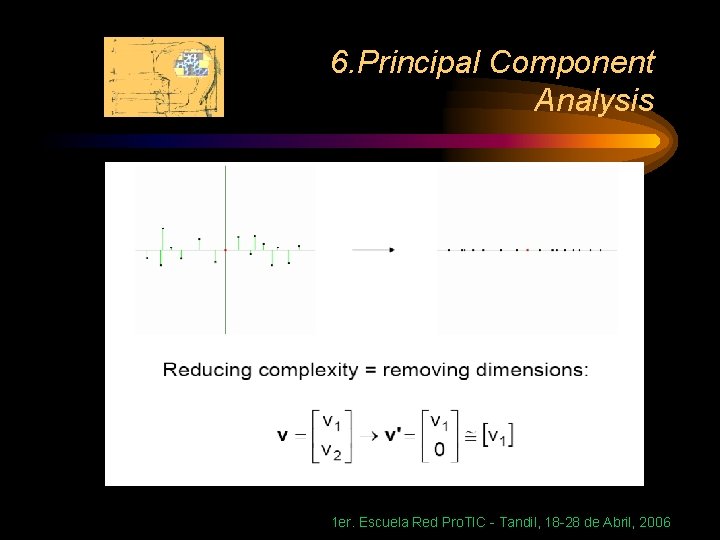
6. Principal Component Analysis Usage of PCA: Data compression Because the kth PC retains the kth greatest fraction of the variation, we can approximate each observation by truncating the sum at the first m < p PCs: 1 er. Escuela Red Pro. TIC - Tandil, 18 -28 de Abril, 2006

6. Principal Component Analysis This reduces the dimensionality of the data from p to m < p by approximating where is the n x m portion of and is the p x m portion of 1 er. Escuela Red Pro. TIC - Tandil, 18 -28 de Abril, 2006
 Independent component analysis vs pca
Independent component analysis vs pca Karl wuensch
Karl wuensch Principal component analysis
Principal component analysis Jmp neural network
Jmp neural network Generalized principal component analysis
Generalized principal component analysis Principal component analysis
Principal component analysis Generalized principal component analysis
Generalized principal component analysis Kernel pca
Kernel pca Disposable pca pump
Disposable pca pump Statquest josh starmer
Statquest josh starmer Pca rmr
Pca rmr Mnchoices assessment ramsey county
Mnchoices assessment ramsey county Ejemplo de pca
Ejemplo de pca Lda vs pca
Lda vs pca Pca observation chart
Pca observation chart Chong ho yu
Chong ho yu Sparse pca
Sparse pca Pca vs ica
Pca vs ica Https://www.retourabsence.bscc.fr
Https://www.retourabsence.bscc.fr Generalized pca
Generalized pca Rmmss
Rmmss Kmo test interpretation
Kmo test interpretation How does umap work
How does umap work Pca vs ica
Pca vs ica Pca introduction
Pca introduction Vincenzo verardi
Vincenzo verardi Pca algorithm steps
Pca algorithm steps Ggfortify pca
Ggfortify pca Is pca unsupervised learning
Is pca unsupervised learning Efa vs cfa
Efa vs cfa Pca logistic regression
Pca logistic regression Pca bcp
Pca bcp Unicef pca guidelines
Unicef pca guidelines Pca crucible
Pca crucible Que es la pca
Que es la pca Pruebas pca
Pruebas pca Que es la pca
Que es la pca Indicadores de la autoestima
Indicadores de la autoestima Que es la pca
Que es la pca Pca example
Pca example Pca
Pca