PCA vs ICA vs LDA How to represent

PCA vs ICA vs LDA

How to represent images? • Why representation methods are needed? ? – Curse of dimensionality – width x height x channels – Noise reduction – Signal analysis & Visualization • Representation methods – Representation in frequency domain : linear transform • DFT, DCT, DST, DWT, … • Used as compression methods – Subspace derivation • PCA, ICA, LDA • Linear transform derived from training data – Feature extraction methods • • • Edge(Line) Detection Feature map obtained by filtering Gabor transform Active contours (Snakes) …

What is subspace? (1/2) • Find a basis in a low dimensional sub-space: − Approximate vectors by projecting them in a low dimensional sub-space: (1) Original space representation: (2) Lower-dimensional sub-space representation: • Note: if K=N, then

What is subspace? (2/2) • Example (K=N):

PRINCIPAL COMPONENT ANALYSIS (PCA)

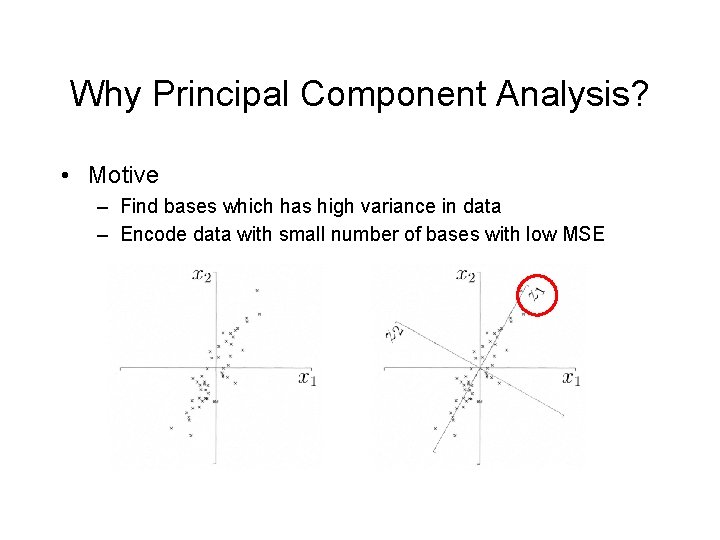
Why Principal Component Analysis? • Motive – Find bases which has high variance in data – Encode data with small number of bases with low MSE

Derivation of PCs Assume that Find q’s maximizing this!! Principal component q can be obtained by Eigenvector decomposition such as SVD!

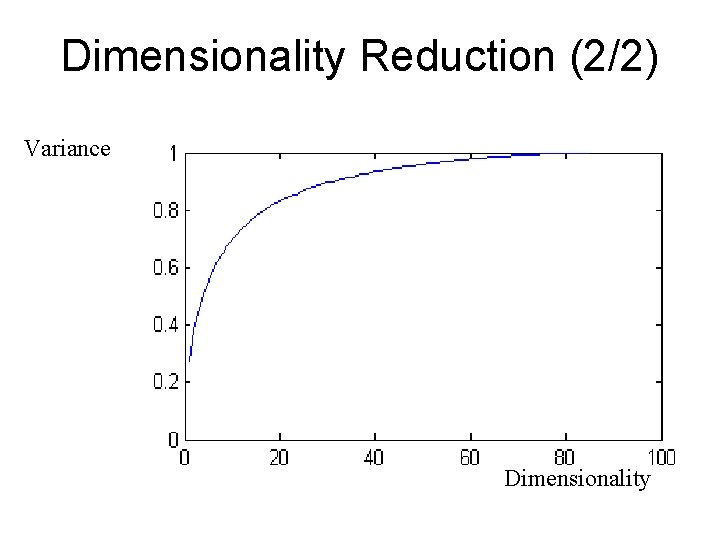
Dimensionality Reduction (1/2) Can ignore the components of less significance. You do lose some information, but if the eigenvalues are small, you don’t lose much – – n dimensions in original data calculate n eigenvectors and eigenvalues choose only the first p eigenvectors, based on their eigenvalues final data set has only p dimensions

Dimensionality Reduction (2/2) Variance Dimensionality

Reconstruction from PCs q=16 q=2 q=32 q=4 q=64 q=8 q=100… Original Image

LINEAR DISCRIMINANT ANALYSIS (LDA)

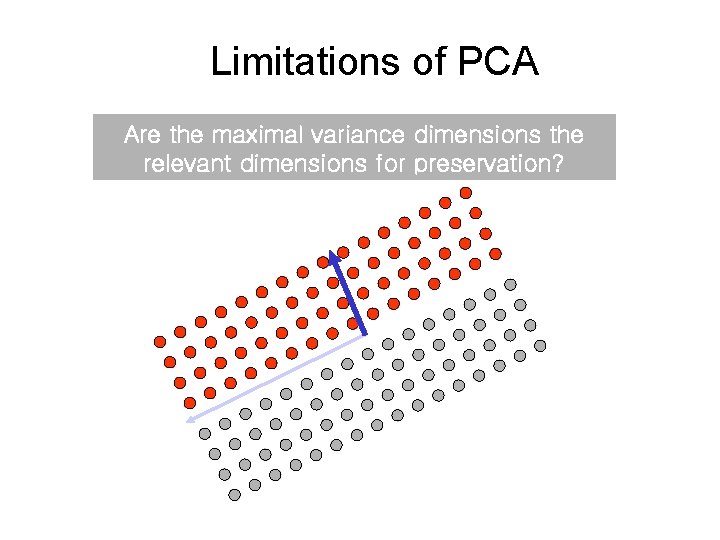
Limitations of PCA Are the maximal variance dimensions the relevant dimensions for preservation?

Linear Discriminant Analysis (1/6) • What is the goal of LDA? − Perform dimensionality reduction “while preserving as much of the class discriminatory information as possible”. − Seeks to find directions along which the classes are best separated. − Takes into consideration the scatter within-classes but also the scatter between-classes. − For example of face recognition, more capable of distinguishing image variation due to identity from variation due to other sources such as illumination and expression.

Linear Discriminant Analysis (2/6) Within-class scatter matrix Between-class scatter matrix projection matrix − LDA computes a transformation that maximizes the between-class scatter while minimizing the within-class scatter: products of eigenvalues ! : scatter matrices of the projected data y

Linear Discriminant Analysis (3/6) • Does Sw-1 always exist? − If Sw is non-singular, we can obtain a conventional eigenvalue problem by writing: − In practice, Sw is often singular since the data are image vectors with large dimensionality while the size of the data set is much smaller (M << N ) − c. f. Since Sb has at most rank C-1, the max number of eigenvectors with non-zero eigenvalues is C-1 (i. e. , max dimensionality of subspace is C-1)

Linear Discriminant Analysis (4/6) • Does Sw-1 always exist? – cont. − To alleviate this problem, we can use PCA first: 1) PCA is first applied to the data set to reduce its dimensionality. 2) LDA is then applied to find the most discriminative directions:

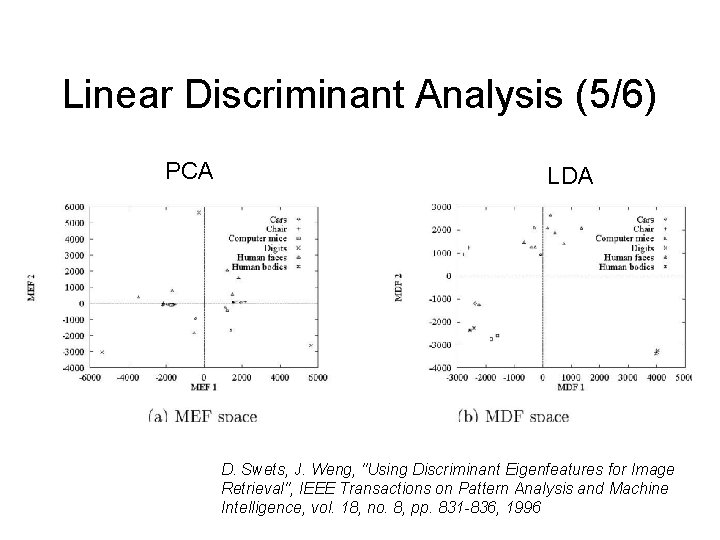
Linear Discriminant Analysis (5/6) PCA LDA D. Swets, J. Weng, "Using Discriminant Eigenfeatures for Image Retrieval", IEEE Transactions on Pattern Analysis and Machine Intelligence, vol. 18, no. 8, pp. 831 -836, 1996

Linear Discriminant Analysis (6/6) • Factors unrelated to classification − MEF vectors show the tendency of PCA to capture major variations in the training set such as lighting direction. − MDF vectors discount those factors unrelated to classification. D. Swets, J. Weng, "Using Discriminant Eigenfeatures for Image Retrieval", IEEE Transactions on Pattern Analysis and Machine Intelligence, vol. 18, no. 8, pp. 831 -836, 1996

INDEPENDENT COMPONENT ANALYSIS

PCA vs ICA • PCA – Focus on uncorrelated and Gaussian components – Second-order statistics – Orthogonal transformation • ICA – Focus on independent and non-Gaussian components – Higher-order statistics – Non-orthogonal transformation

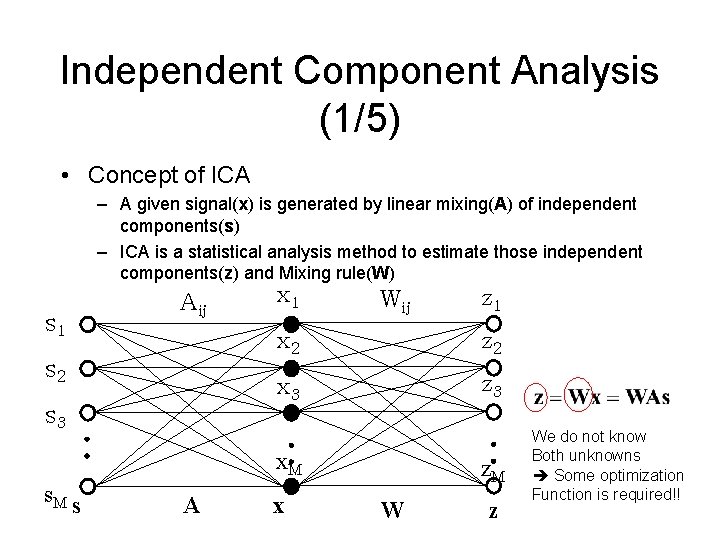
Independent Component Analysis (1/5) • Concept of ICA – A given signal(x) is generated by linear mixing(A) of independent components(s) – ICA is a statistical analysis method to estimate those independent components(z) and Mixing rule(W) s 1 Aij s 2 s 3 x 1 Wij x 2 z 2 x 3 z 3 x. M s A z 1 x z. M W z We do not know Both unknowns Some optimization Function is required!!

Independent Component Analysis (2/5)

Independent Component Analysis(3/5) • What is independent component? ? – If one variable can not be estimated from other variables, it is independent. – By Central Limit Theorem, a sum of two independent random variables is more gaussian than original variables distribution of independent components are nongaussian – To estimate ICs, z should have nongaussian distribution, i. e. we should maximize nonguassianity.

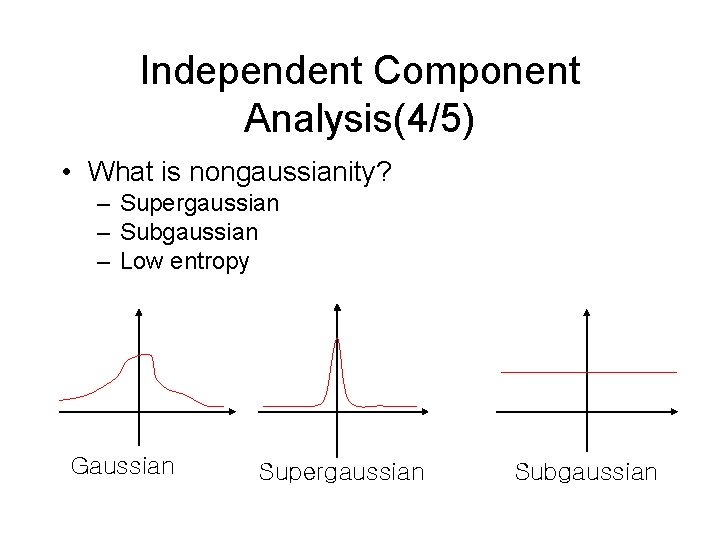
Independent Component Analysis(4/5) • What is nongaussianity? – Supergaussian – Subgaussian – Low entropy Gaussian Supergaussian Subgaussian

Independent Component Analysis(5/5) • Measuring nongaussianity by Kurtosis – Kurtosis : 4 th order cumulant of randomvariable • If kurt(z) is zero, gaussian • If kurt(z) is positive, supergaussian • If kurt(z) is negative, subgaussian • Maximzation of |kurt(z)| by gradient method Simply change The norm of w Fast-fixed point algorithm

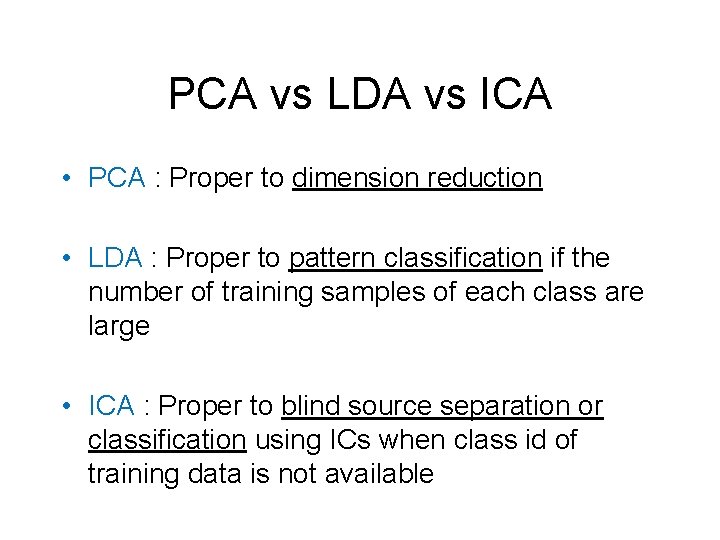
PCA vs LDA vs ICA • PCA : Proper to dimension reduction • LDA : Proper to pattern classification if the number of training samples of each class are large • ICA : Proper to blind source separation or classification using ICs when class id of training data is not available

References • Simon Haykin, “Neural Networks – A Comprehensive Foundation- 2 nd Edition, ” Prentice Hall • Marian Stewart Bartlett, “Face Image Analysis by Unsupervised Learning, ” Kluwer academic publishers • A. Hyvärinen, J. Karhunen and E. Oja, “Independent Component Analysis, ”, John Willy & Sons, Inc. • D. L. Swets and J. Weng, “Using Discriminant Eigenfeatures for Image Retrieval”, IEEE Trasaction on Pattern Analysis and Machine Intelligence, Vol. 18, No. 8, August 1996