Multivariate statistics PCA principal component analysis Correspondence analysis

Multivariate statistics • • • PCA: principal component analysis Correspondence analysis Canonical correlation Discriminant function analysis Cluster analysis MANOVA Xuhua Xia Slide 1

PCA • Given a set of variables x 1, x 2, …, xn, – find a set of coefficients a 11, a 12, …, a 1 n, so that PC 1 = a 11 x 1 + a 12 x 2 + …+ a 1 nxn has the maximum variance (v 1) subject to the constraint that a 1 is a unit vector, i. e. , sqrt(a 112+ a 122 …+ a 1 n 2) = 1 – find a 2 nd set of coefficients a 2 so that PC 2 has the maximum variance (v 2) subject to the unit vector constraint and the additional constraint that a 2 is orthogonal to a 1 – find 3 rd, 4 th, … nth set of coefficients so that PC 3, PC 4, … have the maximum variance (v 3, v 4, …) subject to the unit vector constraint and that ai is orthogonal to all ai-1 vectors. – It turns out that v 1, v 2, … are eigenvalues and a 1, a 2, … are eigenvectors of the variance-covariance matrix of x 1, x 2, …, xn • PCA is to find the eigenvalues and eigenvectors. Slide 2

Typical Form of Data A data set in a 8 x 3 matrix. The rows could be species and columns sampling sites. 100 97 99 96 90 90 80 75 60 75 85 95 X= 62 40 28 77 80 78 92 91 80 75 85 100 A matrix is often referred to as a nxp matrix (n for number of rows and p for number of columns). Our matrix has 8 rows and 3 columns, and is an 8 x 3 matrix. A variance-covariance matrix has n = p, and is called n-dimensional square matrix. Xuhua Xia Slide 3

What are Principal Components? PC = a 1 X 1 + a 2 X 2 + … an. Xn • Principal components are linear combinations of the observed variables. The coefficients of these principal components are chosen to meet four criteria • What are the four criteria? Xuhua Xia Slide 4

What are Principal Components? • The four criteria: – There are exactly p principal components (PCs), each being a linear combination of the observed variables; – The PCs are mutually orthogonal (i. e. , perpendicular and uncorrelated); – The components are extracted in order of decreasing variance. – The components are in the form of eigenvalues and eigenvector of unit length. Xuhua Xia Slide 5

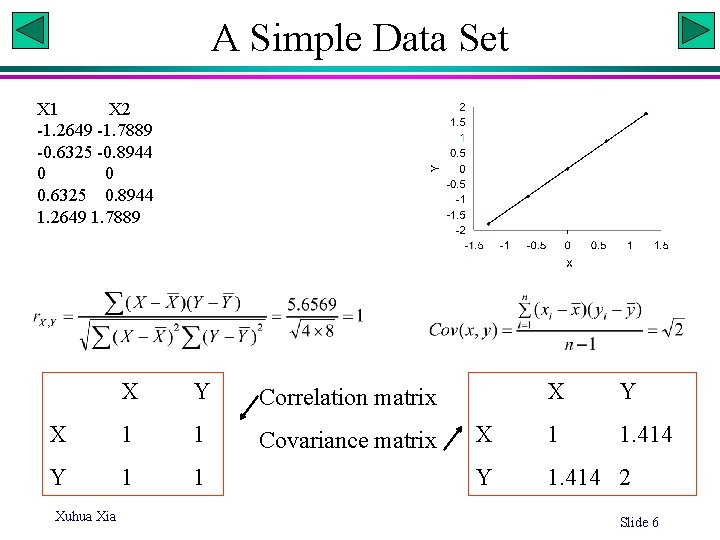
A Simple Data Set X 1 X 2 -1. 2649 -1. 7889 -0. 6325 -0. 8944 0 0 0. 6325 0. 8944 1. 2649 1. 7889 X Y Correlation matrix X 1 1 Covariance matrix Y 1 1 Xuhua Xia X Y X 1 1. 414 Y 1. 414 2 Slide 6

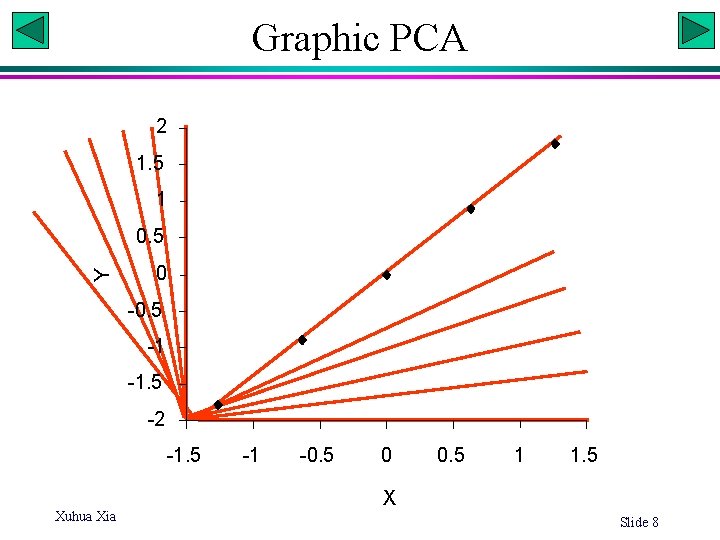
General observations • The total variance is 3 (= 1 + 2) • The two variables, X and Y, are perfectly correlated, with all points fall on the regression line. • The spatial relationship among the 5 points can therefore be represented by a single dimension. • For this reason, PCA is often referred to as a dimension-reduction technique. What would happen if we apply PCA to the data? Xuhua Xia Slide 7

Graphic PCA 2 1. 5 1 Y 0. 5 0 -0. 5 -1 -1. 5 -2 -1. 5 Xuhua Xia -1 -0. 5 0 0. 5 1 1. 5 X Slide 8

R functions X 1 X 2 -1. 2649 -1. 7889 -0. 6325 -0. 8944 0 0 0. 6325 0. 8944 1. 2649 1. 7889 options("scipen"=100, "digits"=6) obj. PCA<-prcomp(~X 1+X 2) obj. PCA<-prcomp(md, scale. =T) predict(obj. PCA, md) predict(obj. PCA, data. frame(X 1=0. 3, X 2=0. 5) screeplot(obj. PCA) Don’t use scientific notation. Requesting the PCA to be carried out on the covariance matrix (default) rather than the correlation matrix. Use scale. =TRUE to request PCA on correlation matrix Help decide how many PCs to keep when there are many variables Xuhua Xia Slide 9

A positive definite matrix • When you run the SAS program, the log file will warn that “The Correlation Matrix is not positive definite. ”. What does that mean? • A symmetric matrix M (such as a correlation matrix or a covariance matrix) is positive definite if z’Mz > 0 for all nonzero vectors z with real entries, where z’ is the transpose of z. • Given our correlation matrix with all entries being 1, it is easy to find z that lead to z’Mz = 0. So the matrix is not positive definite: Replace the correlation matrix with the covariance matrix and solve for z. Xuhua Xia Slide 10

SAS Output Standard deviations: [1] 1. 7320714226 0. 0000440773 Rotation: PC 1 PC 2 X 1 0. 577347 0. 816499 X 2 0. 816499 -0. 577347 [1, ] [2, ] [3, ] [4, ] [5, ] better to output in variance (eigenvalue) accounted for by each PC eigenvectors: PC 1 = 0. 57735 X 1+0. 81650 X 2 PC 1 PC 2 -2. 19092 0. 0000278767 -1. 09545 -0. 0000557540 0. 0000000000 1. 09545 0. 0000557540 2. 19092 -0. 0000278767 Principal component scores What’s the variance in PC 1? Xuhua Xia Slide 11

PCA on correlation matrix (scale. =T) Standard deviations: [1] 1. 4142135619 0. 0000381717 Rotation: PC 1 PC 2 X 1 0. 707107 X 2 0. 707107 -0. 707107 PC 1 PC 2 [1, ] -1. 788850 0. 0000241421 [2, ] -0. 894435 -0. 0000482837 [3, ] 0. 0000000000 [4, ] 0. 894435 0. 0000482837 [5, ] 1. 788850 -0. 0000241421 Xuhua Xia Slide 12

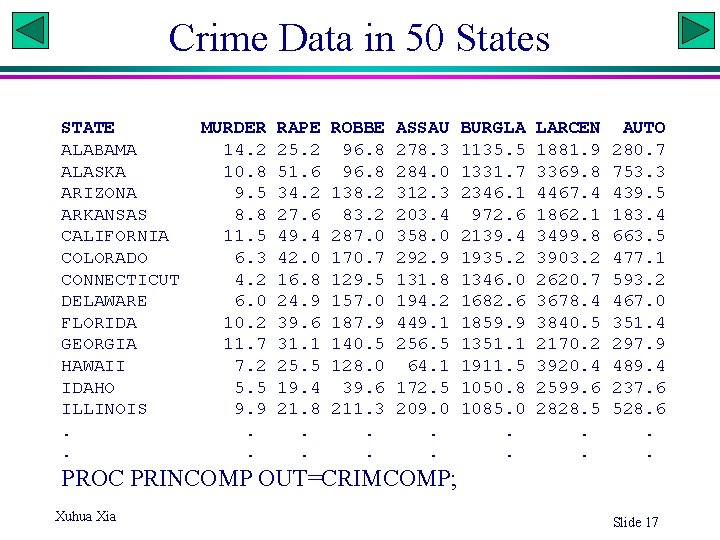
Crime Data in 50 States STATE ALABAMA ALASKA ARIZONA ARKANSAS CALIFORNIA COLORADO CONNECTICUT DELAWARE FLORIDA GEORGIA HAWAII IDAHO ILLINOIS. . MURDER 14. 2 10. 8 9. 5 8. 8 11. 5 6. 3 4. 2 6. 0 10. 2 11. 7 7. 2 5. 5 9. 9. . RAPE 25. 2 51. 6 34. 2 27. 6 49. 4 42. 0 16. 8 24. 9 39. 6 31. 1 25. 5 19. 4 21. 8. . ROBBE 96. 8 138. 2 83. 2 287. 0 170. 7 129. 5 157. 0 187. 9 140. 5 128. 0 39. 6 211. 3. . ASSAU 278. 3 284. 0 312. 3 203. 4 358. 0 292. 9 131. 8 194. 2 449. 1 256. 5 64. 1 172. 5 209. 0. . BURGLA 1135. 5 1331. 7 2346. 1 972. 6 2139. 4 1935. 2 1346. 0 1682. 6 1859. 9 1351. 1 1911. 5 1050. 8 1085. 0. . LARCEN 1881. 9 3369. 8 4467. 4 1862. 1 3499. 8 3903. 2 2620. 7 3678. 4 3840. 5 2170. 2 3920. 4 2599. 6 2828. 5. . AUTO 280. 7 753. 3 439. 5 183. 4 663. 5 477. 1 593. 2 467. 0 351. 4 297. 9 489. 4 237. 6 528. 6. . PROC PRINCOMP OUT=CRIMCOMP; Xuhua Xia Slide 17

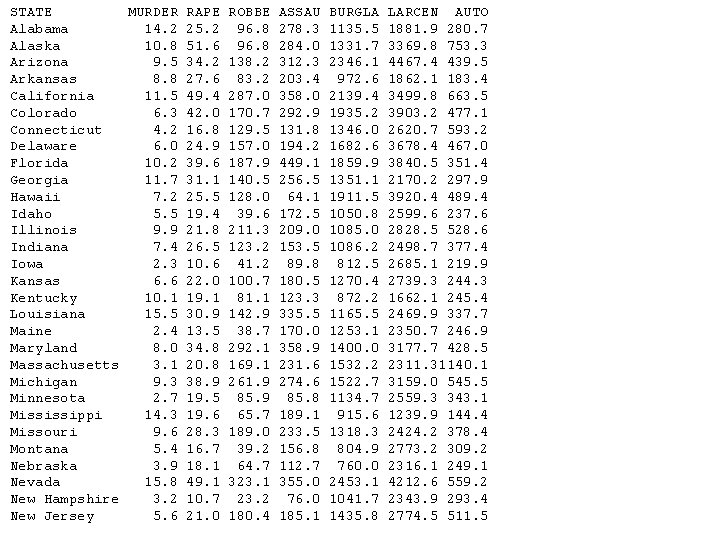
STATE MURDER RAPE ROBBE ASSAU BURGLA LARCEN AUTO Alabama 14. 2 25. 2 96. 8 278. 3 1135. 5 1881. 9 280. 7 Alaska 10. 8 51. 6 96. 8 284. 0 1331. 7 3369. 8 753. 3 Arizona 9. 5 34. 2 138. 2 312. 3 2346. 1 4467. 4 439. 5 Arkansas 8. 8 27. 6 83. 2 203. 4 972. 6 1862. 1 183. 4 California 11. 5 49. 4 287. 0 358. 0 2139. 4 3499. 8 663. 5 Colorado 6. 3 42. 0 170. 7 292. 9 1935. 2 3903. 2 477. 1 Connecticut 4. 2 16. 8 129. 5 131. 8 1346. 0 2620. 7 593. 2 Delaware 6. 0 24. 9 157. 0 194. 2 1682. 6 3678. 4 467. 0 Florida 10. 2 39. 6 187. 9 449. 1 1859. 9 3840. 5 351. 4 Georgia 11. 7 31. 1 140. 5 256. 5 1351. 1 2170. 2 297. 9 Hawaii 7. 2 25. 5 128. 0 64. 1 1911. 5 3920. 4 489. 4 Idaho 5. 5 19. 4 39. 6 172. 5 1050. 8 2599. 6 237. 6 Illinois 9. 9 21. 8 211. 3 209. 0 1085. 0 2828. 5 528. 6 Indiana 7. 4 26. 5 123. 2 153. 5 1086. 2 2498. 7 377. 4 Iowa 2. 3 10. 6 41. 2 89. 8 812. 5 2685. 1 219. 9 Kansas 6. 6 22. 0 100. 7 180. 5 1270. 4 2739. 3 244. 3 Kentucky 10. 1 19. 1 81. 1 123. 3 872. 2 1662. 1 245. 4 Louisiana 15. 5 30. 9 142. 9 335. 5 1165. 5 2469. 9 337. 7 Maine 2. 4 13. 5 38. 7 170. 0 1253. 1 2350. 7 246. 9 Maryland 8. 0 34. 8 292. 1 358. 9 1400. 0 3177. 7 428. 5 Massachusetts 3. 1 20. 8 169. 1 231. 6 1532. 2 2311. 31140. 1 Michigan 9. 3 38. 9 261. 9 274. 6 1522. 7 3159. 0 545. 5 Minnesota 2. 7 19. 5 85. 9 85. 8 1134. 7 2559. 3 343. 1 Mississippi 14. 3 19. 6 65. 7 189. 1 915. 6 1239. 9 144. 4 Missouri 9. 6 28. 3 189. 0 233. 5 1318. 3 2424. 2 378. 4 Montana 5. 4 16. 7 39. 2 156. 8 804. 9 2773. 2 309. 2 Nebraska 3. 9 18. 1 64. 7 112. 7 760. 0 2316. 1 249. 1 Nevada 15. 8 49. 1 323. 1 355. 0 2453. 1 4212. 6 559. 2 New Hampshire 3. 2 10. 7 23. 2 76. 0 1041. 7 2343. 9 293. 4 New Jersey 5. 6 21. 0 180. 4 185. 1 1435. 8 2774. 5 511. 5

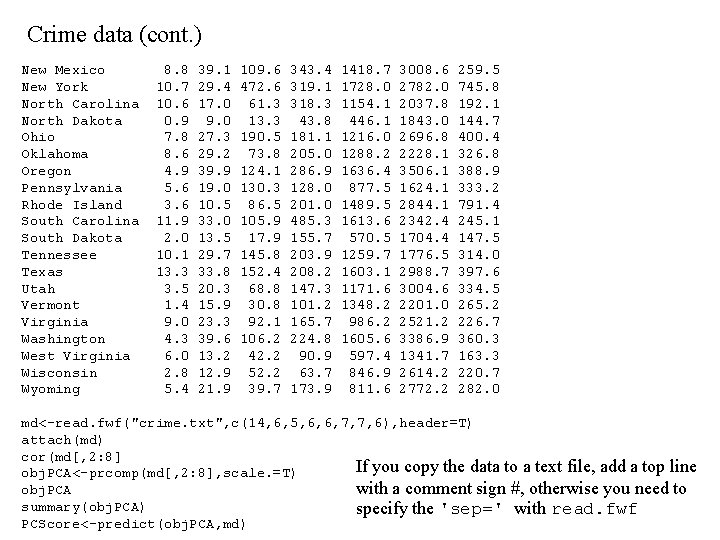
Crime data (cont. ) New Mexico New York North Carolina North Dakota Ohio Oklahoma Oregon Pennsylvania Rhode Island South Carolina South Dakota Tennessee Texas Utah Vermont Virginia Washington West Virginia Wisconsin Wyoming 8. 8 10. 7 10. 6 0. 9 7. 8 8. 6 4. 9 5. 6 3. 6 11. 9 2. 0 10. 1 13. 3 3. 5 1. 4 9. 0 4. 3 6. 0 2. 8 5. 4 39. 1 29. 4 17. 0 9. 0 27. 3 29. 2 39. 9 19. 0 10. 5 33. 0 13. 5 29. 7 33. 8 20. 3 15. 9 23. 3 39. 6 13. 2 12. 9 21. 9 109. 6 472. 6 61. 3 13. 3 190. 5 73. 8 124. 1 130. 3 86. 5 105. 9 17. 9 145. 8 152. 4 68. 8 30. 8 92. 1 106. 2 42. 2 52. 2 39. 7 343. 4 319. 1 318. 3 43. 8 181. 1 205. 0 286. 9 128. 0 201. 0 485. 3 155. 7 203. 9 208. 2 147. 3 101. 2 165. 7 224. 8 90. 9 63. 7 173. 9 1418. 7 1728. 0 1154. 1 446. 1 1216. 0 1288. 2 1636. 4 877. 5 1489. 5 1613. 6 570. 5 1259. 7 1603. 1 1171. 6 1348. 2 986. 2 1605. 6 597. 4 846. 9 811. 6 3008. 6 2782. 0 2037. 8 1843. 0 2696. 8 2228. 1 3506. 1 1624. 1 2844. 1 2342. 4 1704. 4 1776. 5 2988. 7 3004. 6 2201. 0 2521. 2 3386. 9 1341. 7 2614. 2 2772. 2 259. 5 745. 8 192. 1 144. 7 400. 4 326. 8 388. 9 333. 2 791. 4 245. 1 147. 5 314. 0 397. 6 334. 5 265. 2 226. 7 360. 3 163. 3 220. 7 282. 0 md<-read. fwf("crime. txt", c(14, 6, 5, 6, 6, 7, 7, 6), header=T) attach(md) cor(md[, 2: 8] If you copy the data to a text file, add a top line obj. PCA<-prcomp(md[, 2: 8], scale. =T) with a comment sign #, otherwise you need to obj. PCA summary(obj. PCA) specify the 'sep=' with read. fwf PCScore<-predict(obj. PCA, md)

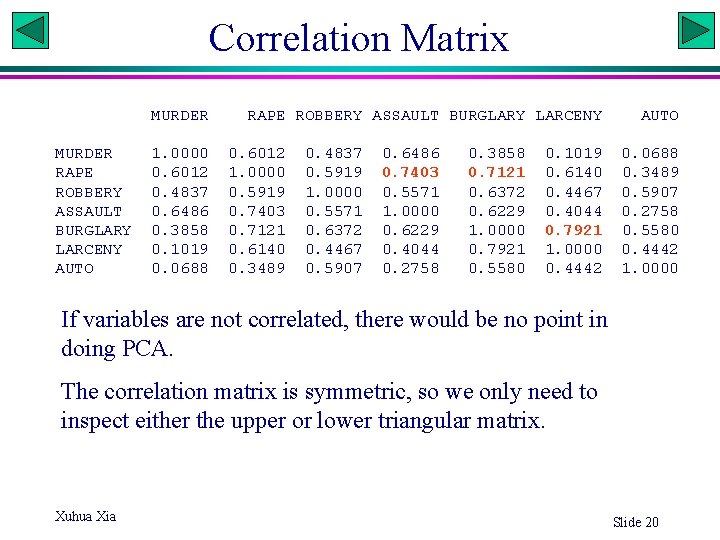
Correlation Matrix MURDER RAPE ROBBERY ASSAULT BURGLARY LARCENY AUTO 1. 0000 0. 6012 0. 4837 0. 6486 0. 3858 0. 1019 0. 0688 RAPE ROBBERY ASSAULT BURGLARY LARCENY 0. 6012 1. 0000 0. 5919 0. 7403 0. 7121 0. 6140 0. 3489 0. 4837 0. 5919 1. 0000 0. 5571 0. 6372 0. 4467 0. 5907 0. 6486 0. 7403 0. 5571 1. 0000 0. 6229 0. 4044 0. 2758 0. 3858 0. 7121 0. 6372 0. 6229 1. 0000 0. 7921 0. 5580 0. 1019 0. 6140 0. 4467 0. 4044 0. 7921 1. 0000 0. 4442 AUTO 0. 0688 0. 3489 0. 5907 0. 2758 0. 5580 0. 4442 1. 0000 If variables are not correlated, there would be no point in doing PCA. The correlation matrix is symmetric, so we only need to inspect either the upper or lower triangular matrix. Xuhua Xia Slide 20

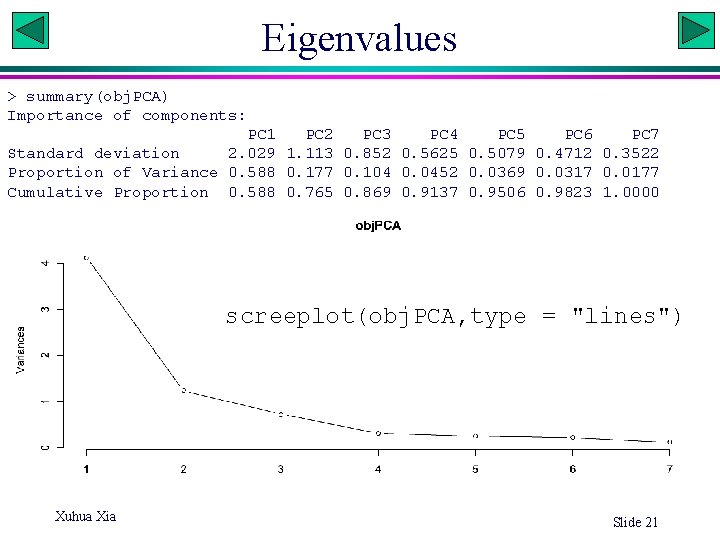
Eigenvalues > summary(obj. PCA) Importance of components: PC 1 PC 2 PC 3 PC 4 PC 5 PC 6 PC 7 Standard deviation 2. 029 1. 113 0. 852 0. 5625 0. 5079 0. 4712 0. 3522 Proportion of Variance 0. 588 0. 177 0. 104 0. 0452 0. 0369 0. 0317 0. 0177 Cumulative Proportion 0. 588 0. 765 0. 869 0. 9137 0. 9506 0. 9823 1. 0000 screeplot(obj. PCA, type = "lines") Xuhua Xia Slide 21

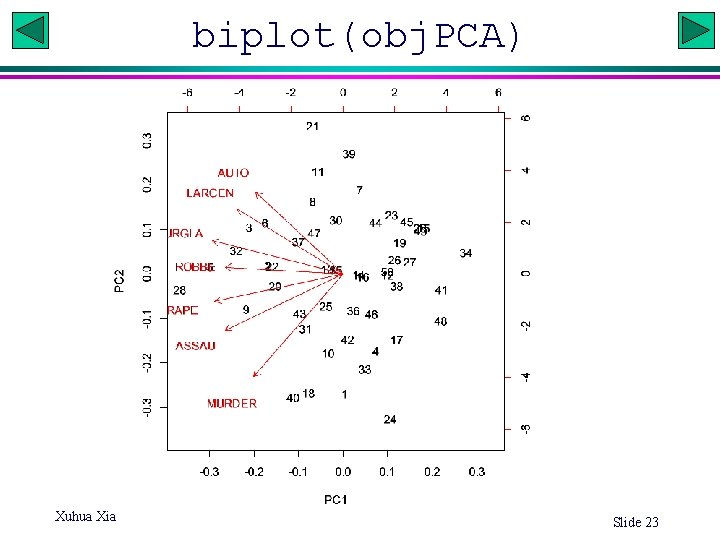
Eigenvectors PC 1 PC 2 PC 3 PC 4 PC 5 PC 6 PC 7 MURDER -0. 3003 -0. 62918 0. 17824 -0. 23216 0. 53810 0. 25912 0. 267589 RAPE -0. 4318 -0. 16944 -0. 24421 0. 06219 0. 18848 -0. 77327 -0. 296490 ROBBE -0. 3969 0. 04224 0. 49588 -0. 55793 -0. 52002 -0. 11439 -0. 003902 ASSAU -0. 3966 -0. 34353 -0. 06953 0. 62984 -0. 50660 0. 17235 0. 191751 BURGLA -0. 4402 0. 20334 -0. 20990 -0. 05757 0. 10101 0. 53599 -0. 648117 LARCEN -0. 3574 0. 40233 -0. 53922 -0. 23491 0. 03008 0. 03941 0. 601688 AUTO -0. 2952 0. 50241 0. 56837 0. 41922 0. 36980 -0. 05729 0. 147044 • Do these eigenvectors mean anything? – All crimes are negatively correlated with the first eigenvector, which is therefore interpreted as a measure of overall safety. – The 2 nd eigenvector has positive loadings on AUTO, LARCENY and ROBBERY and negative loadings on MURDER, ASSAULT and RAPE. It is interpreted to measure the preponderance of property crime over violent crime…. . . Xuhua Xia Slide 22

biplot(obj. PCA) Xuhua Xia Slide 23

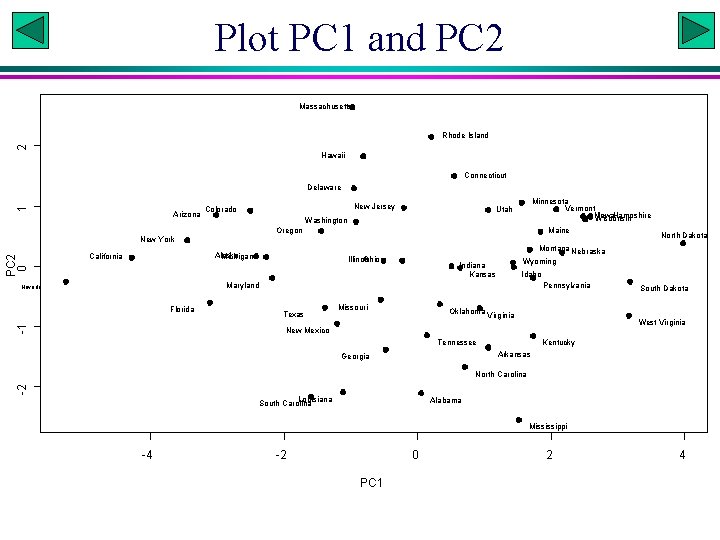
Plot PC 1 and PC 2 Massachusetts 2 Rhode Island Hawaii Connecticut 1 Delaware Arizona New Jersey Colorado Minnesota Vermont New Iowa. Hampshire Wisconsin Utah Washington Oregon Maine PC 2 0 New York Alaska Michigan California Illinois Ohio Wyoming Indiana Kansas Idaho Maryland Nevada -1 Florida Pennsylvania Texas North Dakota Montana Nebraska Missouri Oklahoma Virginia South Dakota West Virginia New Mexico Tennessee Kentucky Arkansas Georgia -2 North Carolina Louisiana South Carolina Alabama Mississippi -4 -2 0 PC 1 2 4

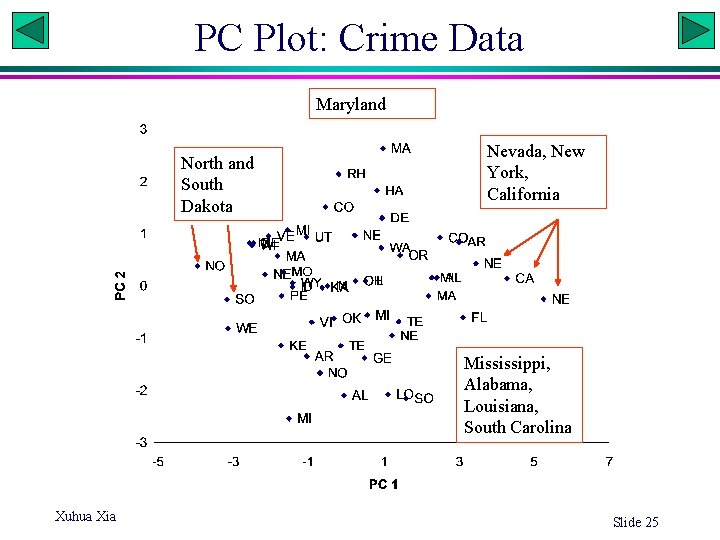
PC Plot: Crime Data Maryland North and South Dakota Nevada, New York, California Mississippi, Alabama, Louisiana, South Carolina Xuhua Xia Slide 25

Steps in a PCA • • • Generate a correlation or variance-covariance matrix Obtain eigenvalues and eigenvectors Generate principal component (PC) scores Choose the number of PCs Plot the PC scores in the space with reduced dimensions Xuhua Xia Slide 26