Unsupervised Learning NEt WORKS PCA NETWORK PCA is





![Oja Learning Rule Δw(t) = β [x(t)a(t) - w(t) 2 a(t) ] the Oja Oja Learning Rule Δw(t) = β [x(t)a(t) - w(t) 2 a(t) ] the Oja](https://slidetodoc.com/presentation_image/523a5b0f003fa35d7ceab622b813c667/image-7.jpg)


![Proof: Δw(t) = β [x(t)a(t) - w(t) a(t)2] Δw(t) = β [x(t)x’(t)w(t) - a(t)2 Proof: Δw(t) = β [x(t)a(t) - w(t) a(t)2] Δw(t) = β [x(t)x’(t)w(t) - a(t)2](https://slidetodoc.com/presentation_image/523a5b0f003fa35d7ceab622b813c667/image-10.jpg)
![Convergence Rates Θ(ť) = [θ 1(ť) θ 2(ť) … θn(ť)]T Each of the eigen-components Convergence Rates Θ(ť) = [θ 1(ť) θ 2(ť) … θn(ť)]T Each of the eigen-components](https://slidetodoc.com/presentation_image/523a5b0f003fa35d7ceab622b813c667/image-11.jpg)






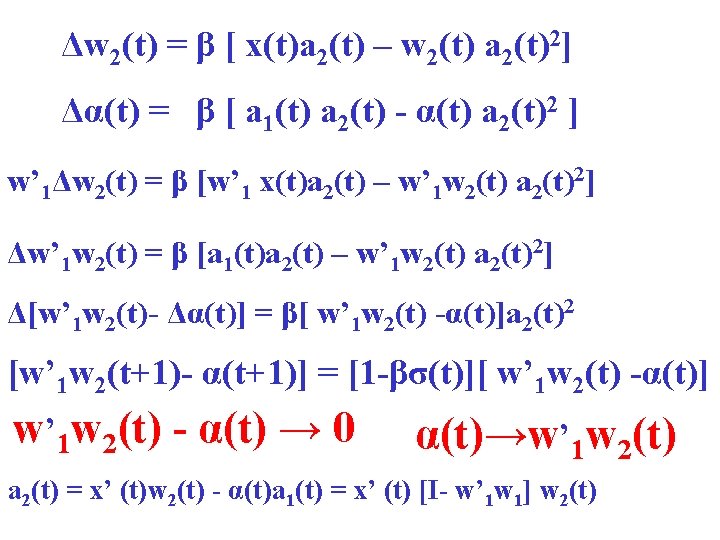


- Slides: 23

Unsupervised Learning NEt. WORKS • PCA NETWORK

PCA is a Representation Network useful for signal, image, video processing

PCA NEt. WORKS In order to analyze multi-dimensional input vectors, a representation with maximum information is the principal component analysis (PCA). PCA • per component: extract most significant features, • inter-component: avoid duplication or redundancy between the neurons.

An estimate of the autocorrelation matrix by taking the time average over the sample vectors: Rx Řx = (1/M ) Σt x(t)xt(t) Rx = t UΛU

the optimal matrix W is formed by the first m singular vectors of Rx. x(t) = W a(t) the errors of the optimal estimate are [Jain 89]: • matrix-2 -norm error = λm+1 • least-mean-square error = Σin=m+1 λi

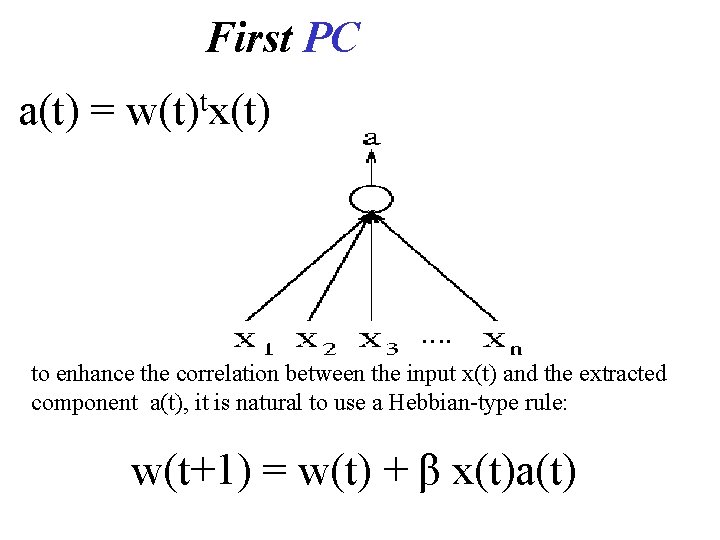
First PC a(t) = t w(t) x(t) to enhance the correlation between the input x(t) and the extracted component a(t), it is natural to use a Hebbian-type rule: w(t+1) = w(t) + β x(t)a(t)
![Oja Learning Rule Δwt β xtat wt 2 at the Oja Oja Learning Rule Δw(t) = β [x(t)a(t) - w(t) 2 a(t) ] the Oja](https://slidetodoc.com/presentation_image/523a5b0f003fa35d7ceab622b813c667/image-7.jpg)
Oja Learning Rule Δw(t) = β [x(t)a(t) - w(t) 2 a(t) ] the Oja learning Rule is equivalent to a normalized Hebbian rule. (Show procedure!!)


Convergence theorem: Single Component By the Oja learning rule, w(t) converges asymptotically (with probability 1) to w = w(∞) = e 1 where e 1 is the principal eigenvector of Rx
![Proof Δwt β xtat wt at2 Δwt β xtxtwt at2 Proof: Δw(t) = β [x(t)a(t) - w(t) a(t)2] Δw(t) = β [x(t)x’(t)w(t) - a(t)2](https://slidetodoc.com/presentation_image/523a5b0f003fa35d7ceab622b813c667/image-10.jpg)
Proof: Δw(t) = β [x(t)a(t) - w(t) a(t)2] Δw(t) = β [x(t)x’(t)w(t) - a(t)2 w(t)] take average over a block of data, and redenote ť as the block time index: Δw(ť) = β [Rx - σ(ť)I] w(ť) Δw(ť) = β [UΛUT - σ(ť)I] w(ť) Δw(ť) = β U[Λ - σ(ť)I] UT w(ť) ΔUTw(ť) = β [Λ - σ(ť)I] UTw(ť) ΔΘ(ť) = β [Λ - σ(ť)I] Θ (ť)
![Convergence Rates Θť θ 1ť θ 2ť θnťT Each of the eigencomponents Convergence Rates Θ(ť) = [θ 1(ť) θ 2(ť) … θn(ť)]T Each of the eigen-components](https://slidetodoc.com/presentation_image/523a5b0f003fa35d7ceab622b813c667/image-11.jpg)
Convergence Rates Θ(ť) = [θ 1(ť) θ 2(ť) … θn(ť)]T Each of the eigen-components is enhanced/dampened by θi(ť+1) = [1+β' λi - β' σ(ť)] θi(ť) the relative dominance of the principle component grows, with a growth rate: (1+β' [λi-σ(ť)])/(1+β' [λ 1 - σ(ť)])

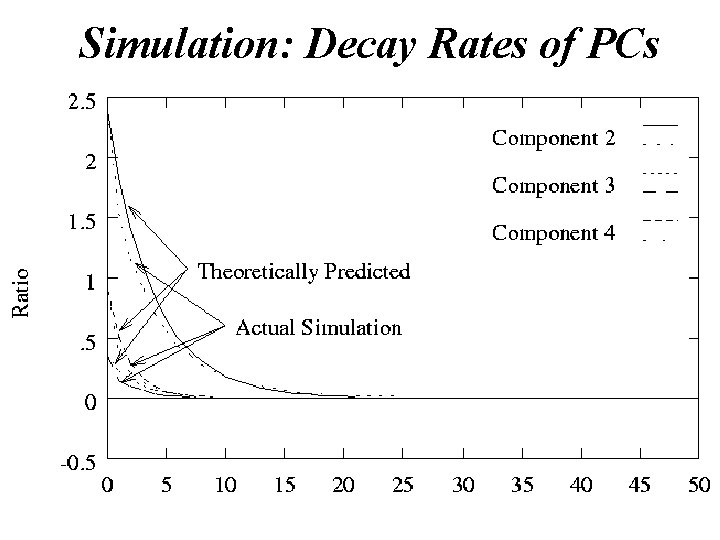
Simulation: Decay Rates of PCs

How to extract Multiple Principal Components

Let W denote a n m weight matrix ΔW(t) = β [x(t) - W(t) a(t)] a(t)t Concern on duplication/redundancy

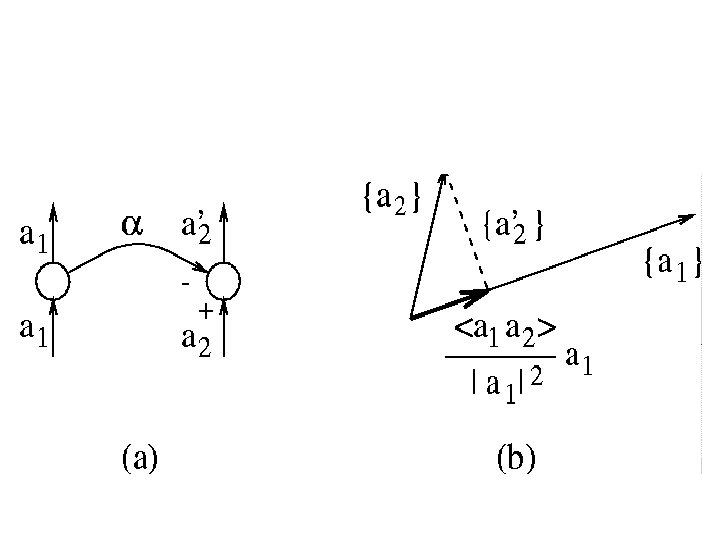
Deflation Method Assume that the first component is already obtained; then the output value can be ``deflated'' by the following transformation: x˜ = (I- w 1 w’ 1) x

Lateral Orthogonalization Network the basic idea is to allow the old hidden units to influence the new units so that the new ones do not duplicate information (in full or in part) already provided by the old units. By this approach, the deflation process is effectively implemented in an adaptive manner.


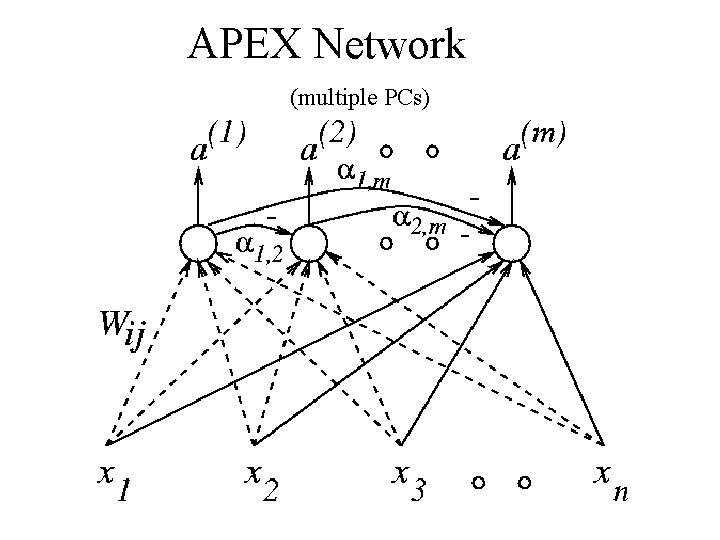
APEX Network (multiple PCs)

APEX: Adaptive Principal-component Extractor the Oja Rule: for i-th component (e. g. i=2) Δwi(t) = β [ x(t)ai(t) - wi(t) ai(t)2] Dynamic Orthogonalization Rule (e. g. i=2, j=1) Δαij(t) = β [ ai(t) aj(t) - αij(t) ai(t)2 ]

Convergence theorem: Multiple Components the Hebbian weight matrix W(t) in APEX converges asymptotically to a matrix formed by the m largest principal components. the weight matrix W(t) converges to (with probability 1), W(∞) = W where W is the matrix formed by m row vectors wit, wi = wi(∞) = ei
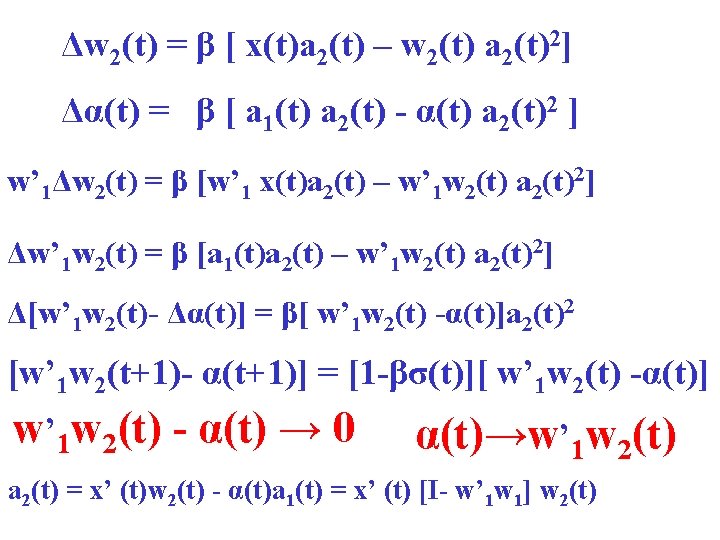


Other Extensions • PAPEX: Hierarchical Extraction • DCA: Discriminant Component Analysis • ICA: Independent Component Analysis