Generalized Principal Component Analysis GPCA Ren Vidal Yi

Generalized Principal Component Analysis (GPCA) René Vidal Yi Ma Shankar Sastry UC Berkeley University of Illinois UC Berkeley

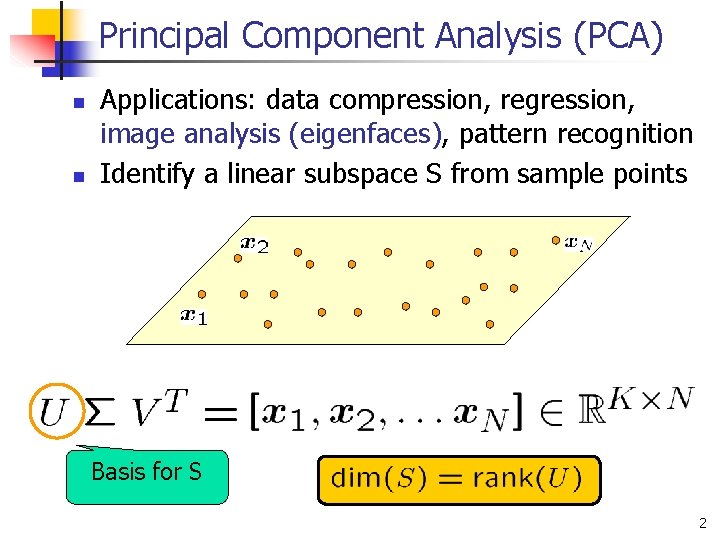
Principal Component Analysis (PCA) n n Applications: data compression, regression, image analysis (eigenfaces), pattern recognition Identify a linear subspace S from sample points Basis for S 2

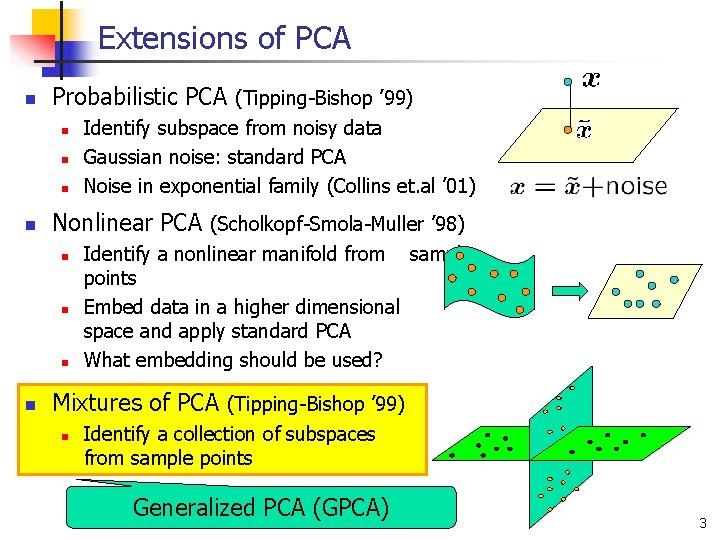
Extensions of PCA n Probabilistic PCA (Tipping-Bishop ’ 99) n n Nonlinear PCA (Scholkopf-Smola-Muller ’ 98) n n Identify subspace from noisy data Gaussian noise: standard PCA Noise in exponential family (Collins et. al ’ 01) Identify a nonlinear manifold from sample points Embed data in a higher dimensional space and apply standard PCA What embedding should be used? Mixtures of PCA (Tipping-Bishop ’ 99) n Identify a collection of subspaces from sample points Generalized PCA (GPCA) 3

Some possible applications of GPCA n Geometry n n Segmentation n n Vanishing points Intensity Texture 2 D Motion 3 D Motion Recognition n Faces (Eigenfaces) n n Human activities n n Man - Woman Running, walking Data compression 4

Generalized Principal Component Analysis n Given points on multiple subspaces, identify n n “Chicken-and-egg” problem n n n Given segmentation, estimate subspaces Given subspaces, segment the data Prior work n n n The number of subspaces and their dimension A basis for each subspace The segmentation of the data points Geometric approaches: 2 planes in R 3 (Shizawa-Maze ’ 91) Factorization approaches: (Boult-Brown ‘ 91, Costeira-Kanade ‘ 98, Kanatani ‘ 01) cluster the data+ apply standard PCA to each cluster Iterative algorithms: e. g. K-plane clustering (Bradley’ 00) Probabilistic approaches (Tipping-Bishop ‘ 99): learn the parameters of a mixture model using e. g. EM Initialization? 5

Our approach to segmentation (GPCA) n Towards an analytic solution to segmentation n n We propose an algebraic geometric approach to multilinear data segmentation n Number of subspaces Subspace basis = degree of a polynomial ≈ roots of a polynomial = polynomial factorization In the absence of noise n n Can we estimate ALL subspaces simultaneously using ALL data? When can we do so analytically? In closed form? Is there a formula for the number of subspaces? Use constraints that are independent on the segmentation There is a unique solution which is closed form iff nsubspaces ≤ 4 The exact solution can be computed using linear algebra In the presence of noise n n Algebraic solution can be used to initialize EM Derive an optimal algorithm for zero-mean Gaussian noise in which the E-step is algebraically eliminated 6

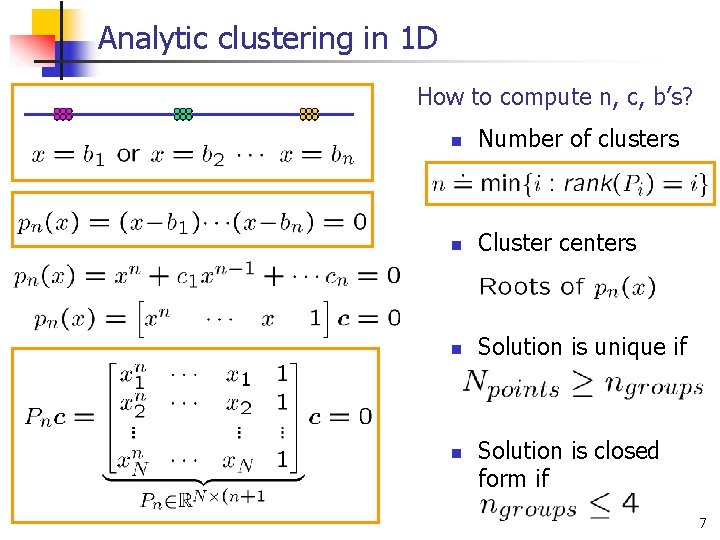
Analytic clustering in 1 D How to compute n, c, b’s? n Number of clusters n Cluster centers n Solution is unique if n Solution is closed form if 7

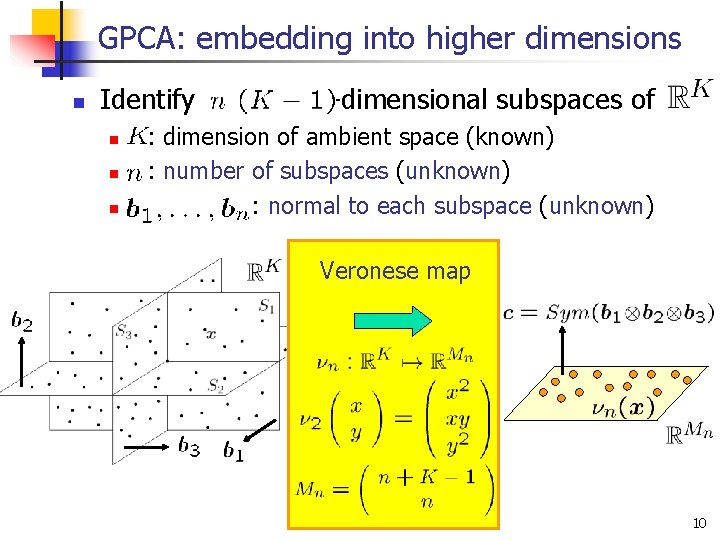
GPCA: embedding into higher dimensions n Identify n n n -dimensional subspaces of : dimension of ambient space (known) : number of subspaces (unknown) : normal to each subspace (unknown) Veronese map 10

GPCA: estimating a model for all subspaces n 1 -dimensional case n K-dimensional case 11

GPCA: estimating individual subspaces n 1 -dimensional case n K-dimensional case Estimate number models: rank of a matrix Estimate individual models: roots/factors of the polynomial Theorem: Generalized PCA [Vidal et al. 2003] n n n Find roots of polynomial of degree in one variable Solve linear systems in variables Solution obtained in closed form for 12

Optimal GPCA n Zero-mean Gaussian noise Minimize distance from noisy data to noise free data subject to segmentation constraints n Using Langrange optimization n After some algebra n 14

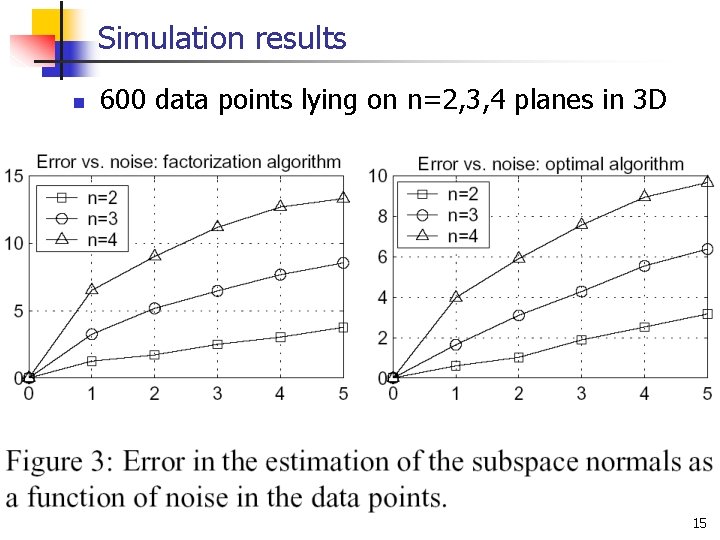
Simulation results n 600 data points lying on n=2, 3, 4 planes in 3 D 15

Segmentation of 2 D translational motions n n n Scene having multiple optical flows Brightness constancy constraint (BCC) gives GPCA problem with K=3 Multibody brightness constraint constancy 16

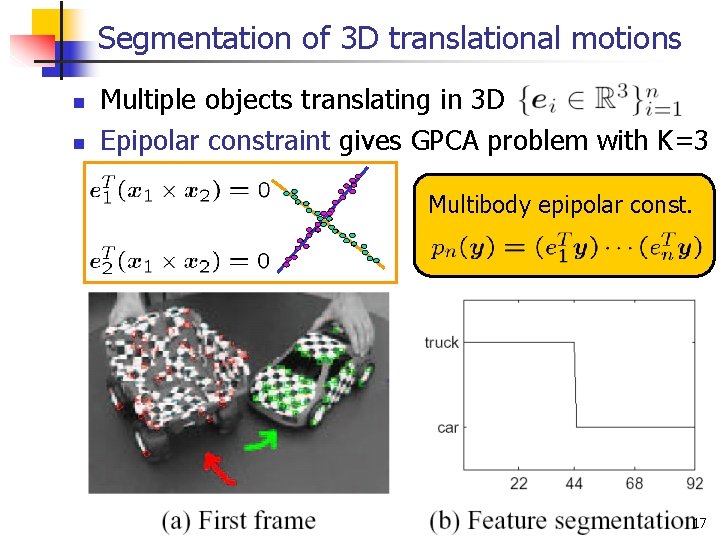
Segmentation of 3 D translational motions n n Multiple objects translating in 3 D Epipolar constraint gives GPCA problem with K=3 Multibody epipolar const. 17

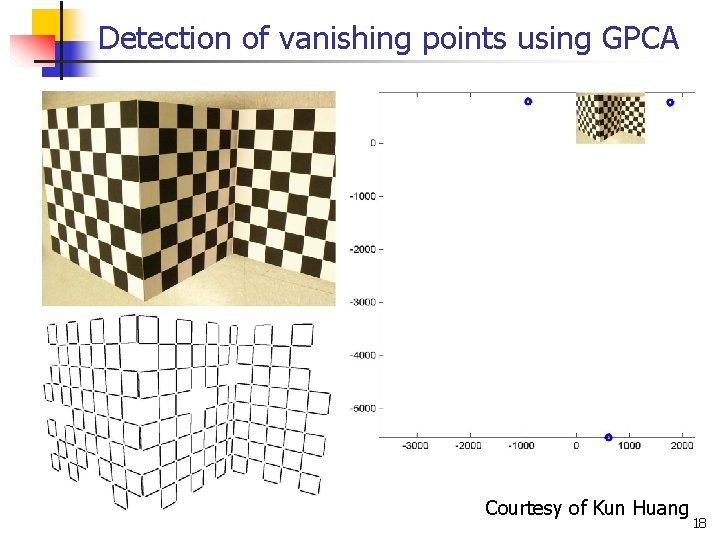
Detection of vanishing points using GPCA Courtesy of Kun Huang 18

Intensity-based image segmentation Black group Gray group White group 147 x 221 Time: 2 (sec) 10 (sec) 0. 4 (sec) 19

Conclusions and ongoing work n Algebraic/geometric approach to simultaneous model estimation and data segmentation for n n Solution based on n Mixtures of subspaces: linear constraints Polynomial factorization: linear algebra Solution is closed form if nsubspaces ≤ 4 Ongoing work n n n Dealing with noisy data and outliers Subspaces of different dimensions Other data types: bilinear constraints, dynamic data n n Optimal Segmentation of Dynamic Scenes (CVPR’ 03) A geometric/statistical theory of segmentation? 20

Texture-based image segmentation GPCA Human 21

Texture-based image segmentation 22

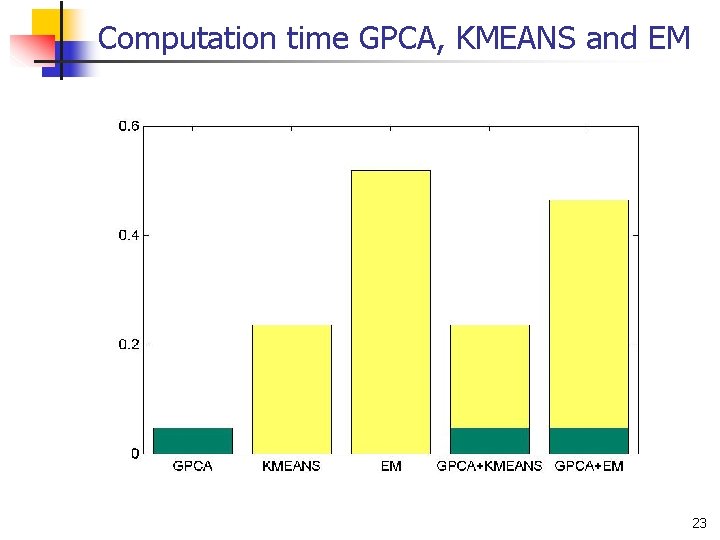
Computation time GPCA, KMEANS and EM 23