Nonnegative polynomials and difference of convex optimization Georgina

Nonnegative polynomials and difference of convex optimization Georgina Hall Princeton, ORFE Joint work with Amir Ali Ahmadi Princeton, ORFE 2/20/2021 IBM May 2016 1

Nonnegative and convex polynomials • Is this polynomial nonnegative?

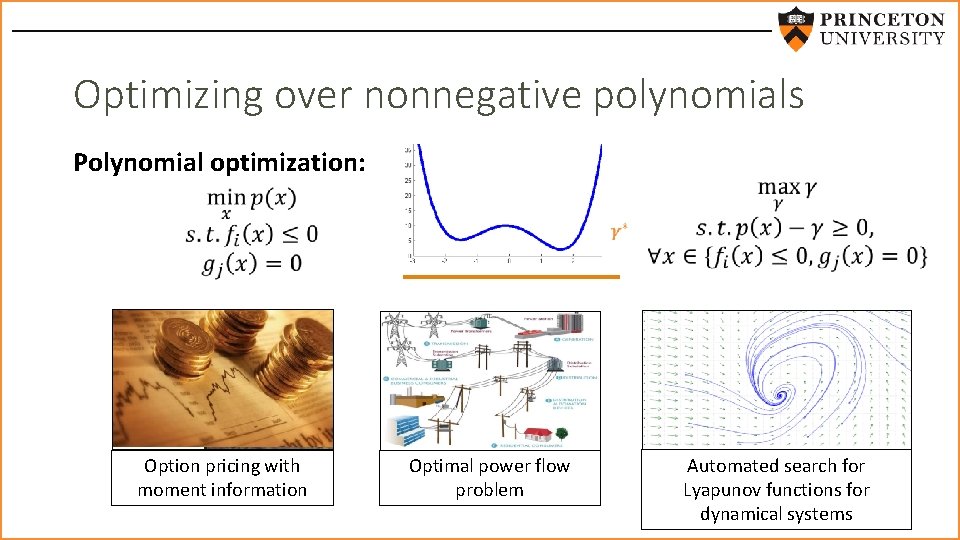
Optimizing over nonnegative polynomials Polynomial optimization: Option pricing with moment information Optimal power flow problem Automated search for Lyapunov functions for dynamical systems

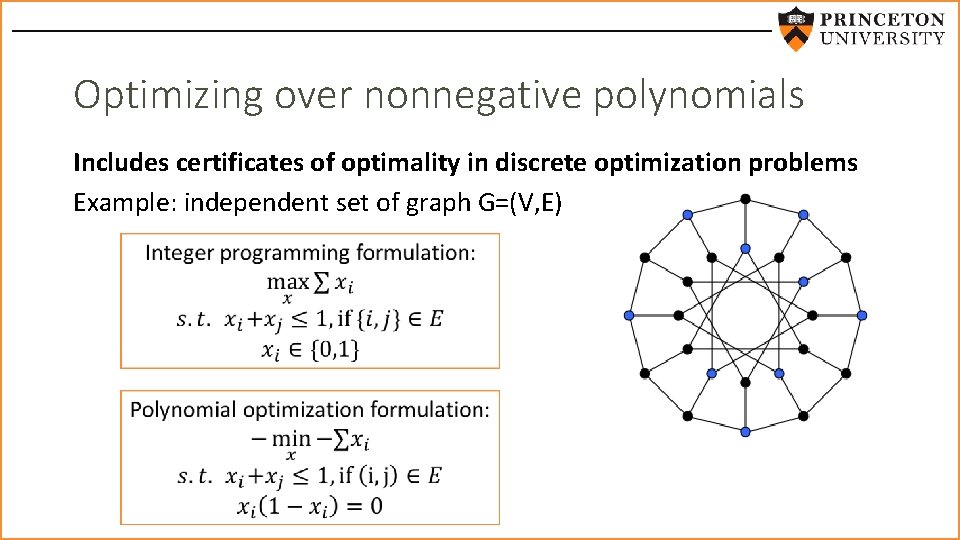
Optimizing over nonnegative polynomials Includes certificates of optimality in discrete optimization problems Example: independent set of graph G=(V, E)

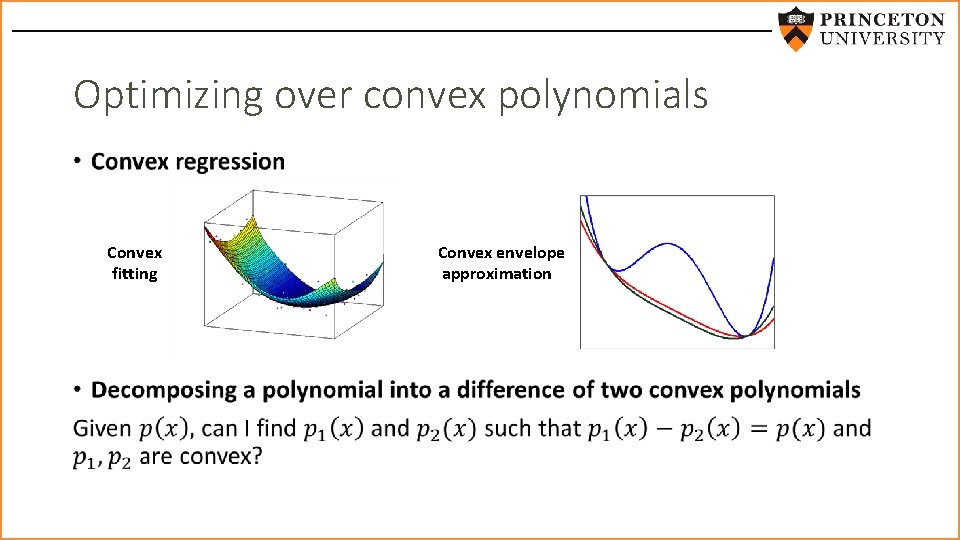
Optimizing over convex polynomials • Convex fitting Convex envelope approximation

Imposing nonnegativity or convexity •

Imposing nonnegativity or convexity • Example:

This talk • Recent efforts to make sos more scalable by avoiding SDP (Ahmadi, Dash, Majumdar) • Using more scalable versions of sum of squares for difference of convex programming

Alternatives to sums-of-squares: dsos and sdsos Sum of squares (sos) SDP Diagonally dominant sum of squares (dsos) LP Scaled diagonally dominant sum of squares (sdsos) SOCP Ahmadi, Majumdar

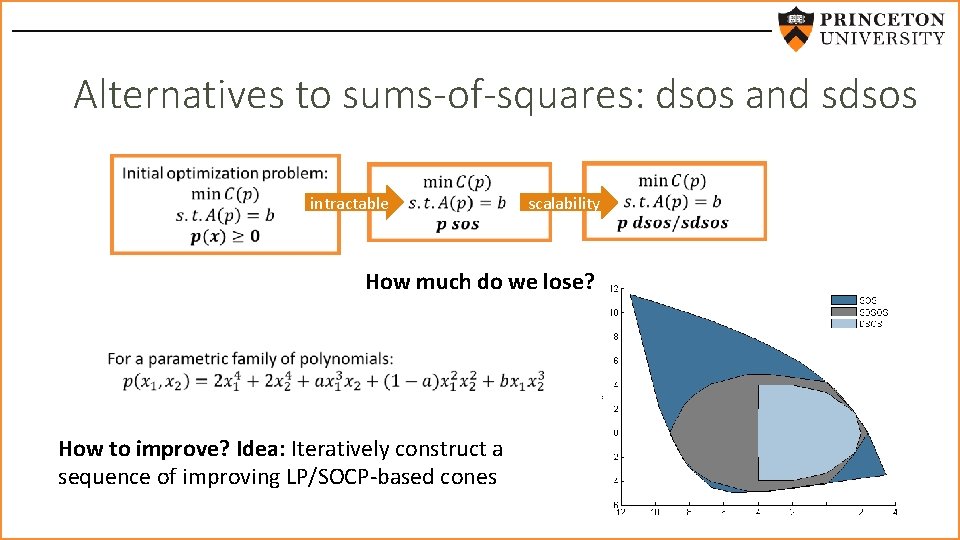
Alternatives to sums-of-squares: dsos and sdsos intractable scalability How much do we lose? How to improve? Idea: Iteratively construct a sequence of improving LP/SOCP-based cones

Cholesky change of basis (1/3) dd in the “right basis” psd but not dd

Cholesky change of basis (2/3) Step 2 Step 1 Initialize Another recent technique: Column Generation method with Sanjeeb Dash.

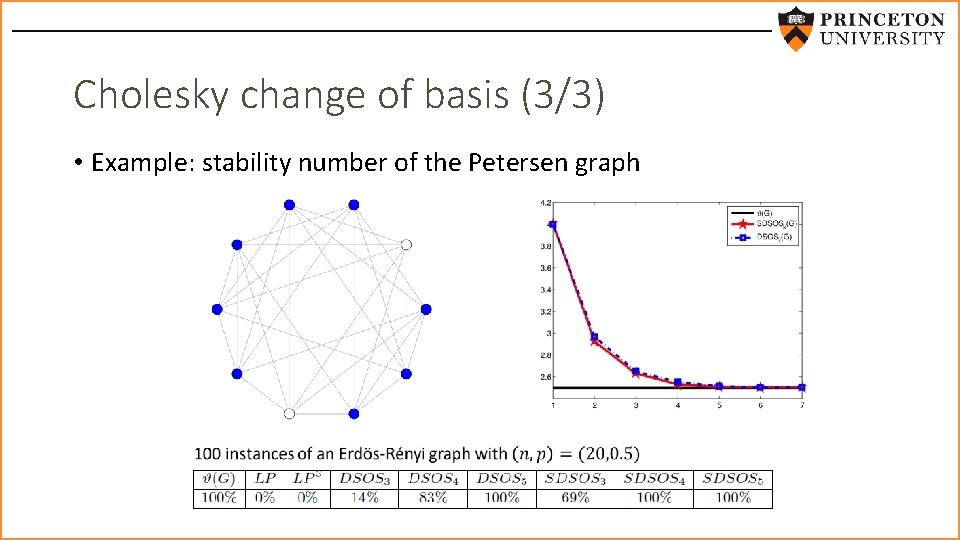
Cholesky change of basis (3/3) • Example: stability number of the Petersen graph

This talk • Recent efforts to make sos more scalable by avoiding SDP (Ahmadi, Dash, Majumdar) • Using more scalable versions of sum of squares for difference of convex programming

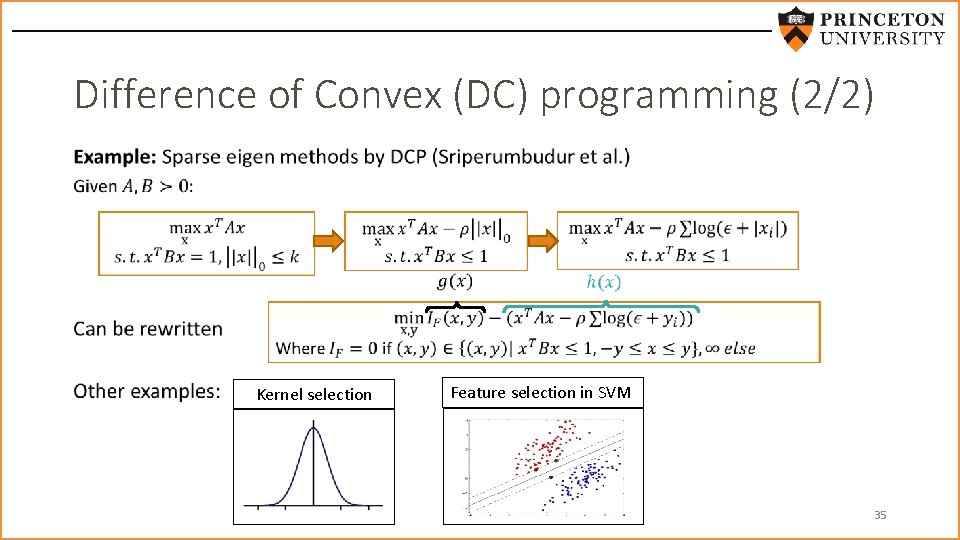
Difference of Convex (DC) programming • Applications: Machine Learning (Sparse PCA, Kernel selection, feature selection in SVM) Hiriart-Urruty, 1985 Tuy, 1995 15

Difference of Convex (dc) decomposition •

Existence of dc decomposition (1/5) Recall: SOS-convexity Theorem: Any polynomial can be written as the difference of two sos-convex polynomials. Corollary: Any polynomial can be written as the difference of two convex polynomials.

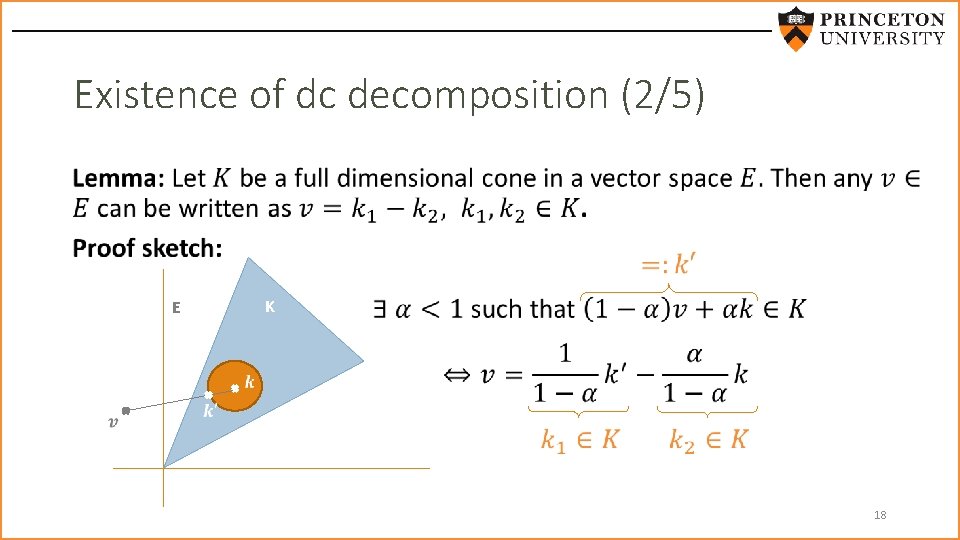
Existence of dc decomposition (2/5) • K E 18

Existence of dc decomposition (3/5) • solving is an SDP.

Existence of dc decomposition (4/5) DSOS-convexity SDSOS-convexity For scalability Theorem: Any polynomial can be written as the difference of two dsos-convex polynomials.

Existence of dc decomposition (5/5) •

Uniqueness of dc decomposition • Initial decomposition Yes Through s/d/sos-convexity Alternative decompositions “Best decomposition? ”

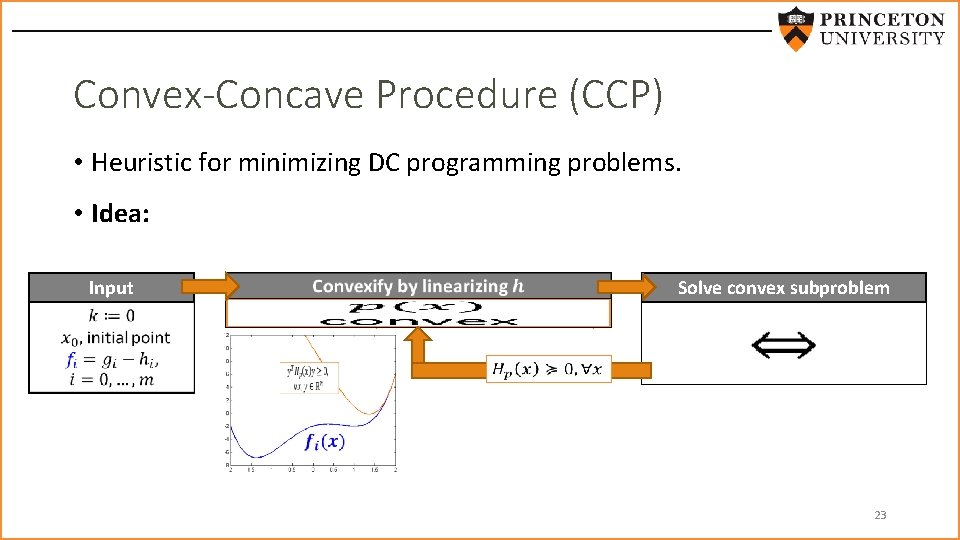
Convex-Concave Procedure (CCP) • Heuristic for minimizing DC programming problems. • Idea: Input Solve convex subproblem convex affine 23

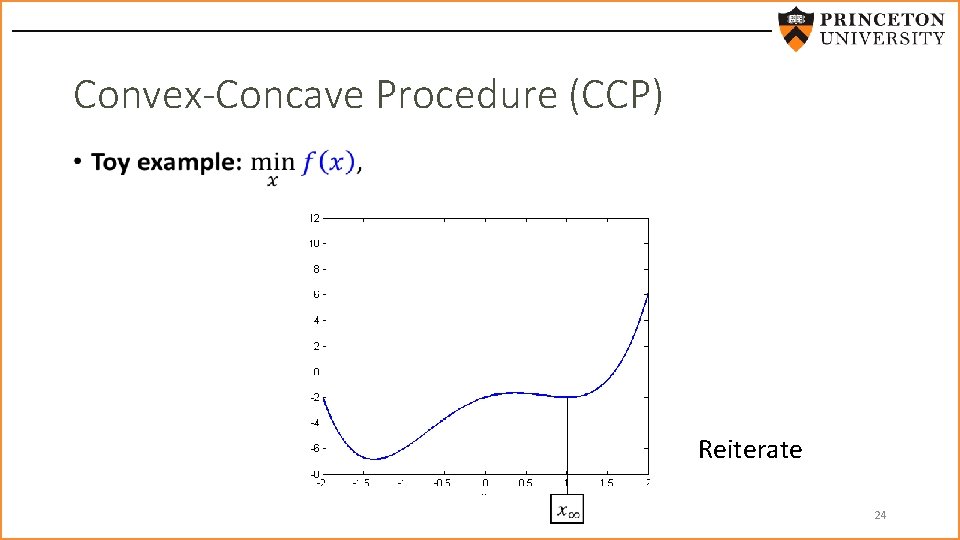
Convex-Concave Procedure (CCP) • Reiterate 24

Picking the “best” decomposition for CCP (1/3) Algorithm Idea Mathematical translation Average curvature* Worst-case curvature* 25

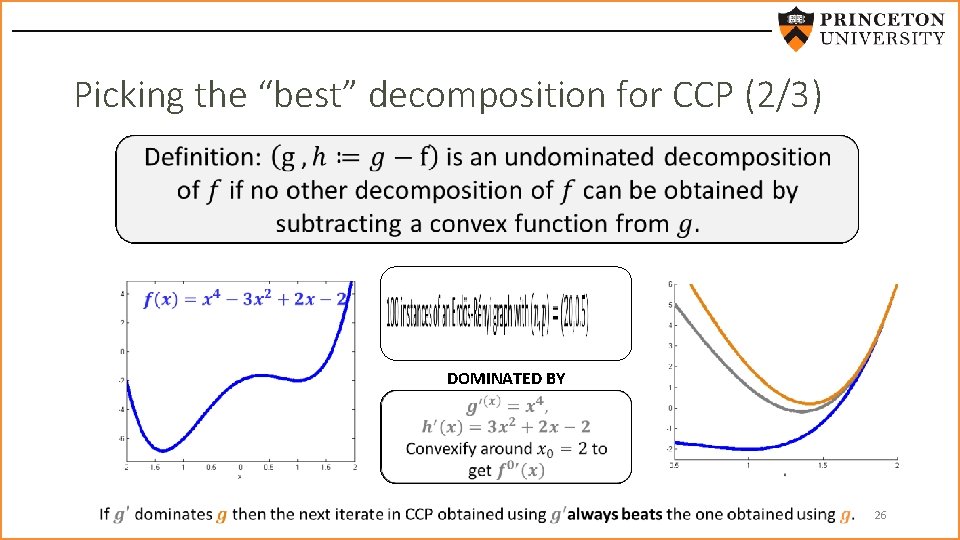
Picking the “best” decomposition for CCP (2/3) DOMINATED BY 26

Picking the “best” decomposition for CCP (3/3) • 27

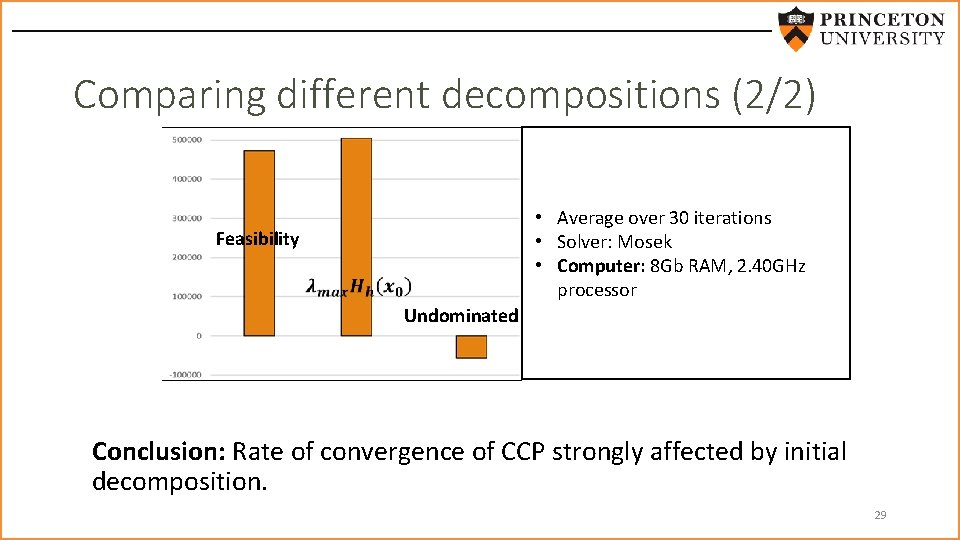
Comparing different decompositions (1/2) • Feasibility Undominated 28

Comparing different decompositions (2/2) • Average over 30 iterations • Solver: Mosek • Computer: 8 Gb RAM, 2. 40 GHz processor Feasibility Undominated Conclusion: Rate of convergence of CCP strongly affected by initial decomposition. 29

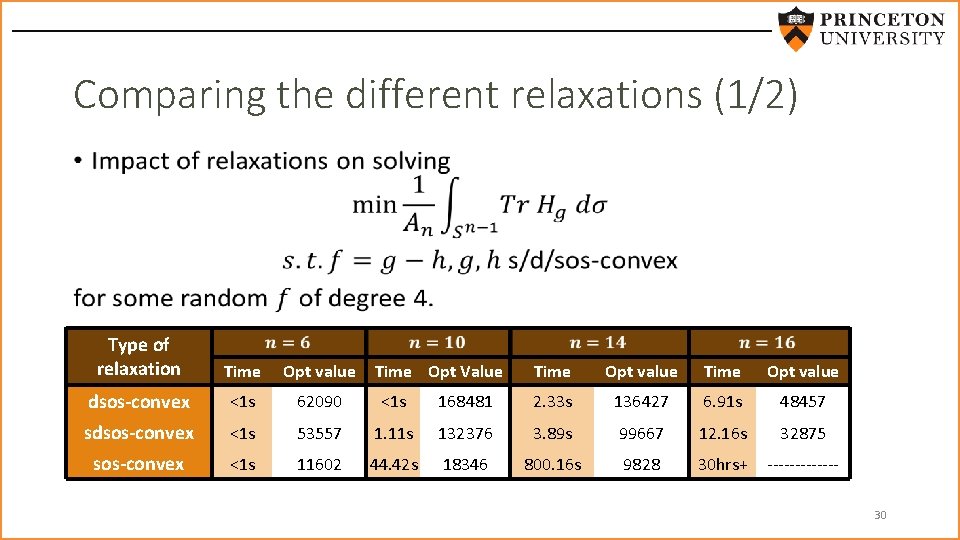
Comparing the different relaxations (1/2) • Type of relaxation Time Opt value dsos-convex <1 s 62090 <1 s sdsos-convex <1 s 53557 sos-convex <1 s 11602 Time Opt Value Time Opt value 168481 2. 33 s 136427 6. 91 s 48457 1. 11 s 132376 3. 89 s 99667 12. 16 s 32875 44. 42 s 18346 800. 16 s 9828 30 hrs+ ------30

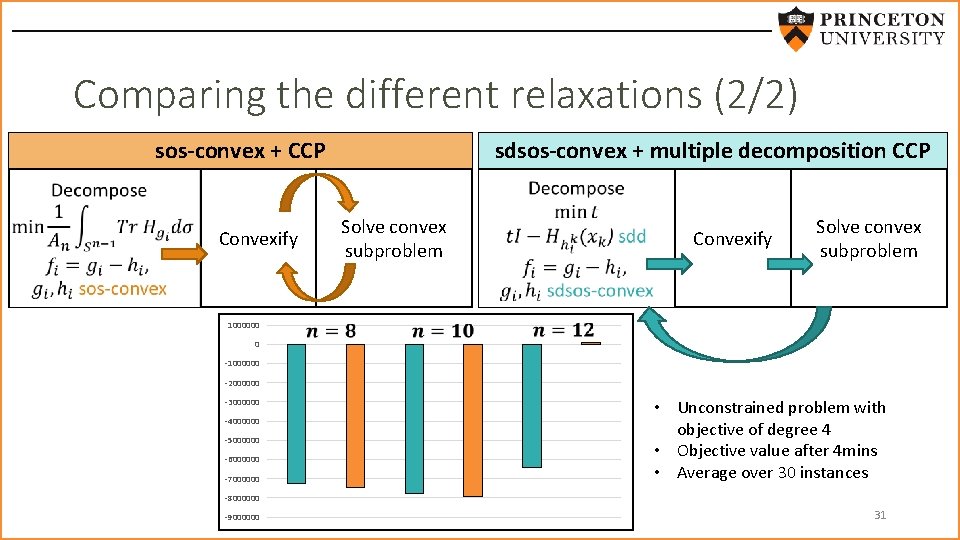
Comparing the different relaxations (2/2) sos-convex + CCP sdsos-convex + multiple decomposition CCP Solve convex subproblem Convexify 1000000 0 Convexify Solve convex subproblem -1000000 -2000000 -3000000 -4000000 -5000000 -6000000 -7000000 • Unconstrained problem with objective of degree 4 • Objective value after 4 mins • Average over 30 instances -8000000 -9000000 31

Main messages • Optimizing over nonnegative and convex polynomials has many applications. • Sum of squares techniques used are SDPs (expensive). • More scalable versions of sum of squares are presented (DSOS, SDSOS, Cholesky Basis method). • Applied these techniques to DCP, to decompose a polynomial into a difference of convex functions. The choice of the decomposition impacts speed of convergence of CCP.

Thank you for listening Questions? Want to learn more? http: //scholar. princeton. edu/ghall/home 33

Existence of difference of convex decomposition (1/4) • How to get round this? SOS-convexity Theorem: Any polynomial can be written as the difference of two sos-convex polynomials.

Difference of Convex (DC) programming (2/2) • Kernel selection Feature selection in SVM 35