EXACT MATRIX COMPLETION VIA CONVEX OPTIMIZATION EMMANUEL J
































- Slides: 34

EXACT MATRIX COMPLETION VIA CONVEX OPTIMIZATION EMMANUEL J. CANDES AND BENJAMIN RECHT MAY 2008 Presenter: Shujie Hou January, 28 th, 2011 Department of Electrical and Computer Engineering Cognitive Radio Institute Tennessee Technological university

SOME AVAILABLE CODES http: //perception. csl. illinois. edu/matrixrank/sample_code. html#RPCA http: //svt. caltech. edu/code. html http: //lmafit. blogs. rice. edu/ http: //www. stanford. edu/~raghuram/optspace/code. html http: //people. ee. duke. edu/~lcarin/BCS. html

OUTLINE The problem statement Examples of impossible recovery Algorithms Main theorems Proof Experimental results Discussion

PROBLEM CONSIDERED The problem of low-rank matrix completion: � Recovery of a data matrix from a sampling of its entries. � A matrix with rows and columns � Only observing a number of of its entries which is much smaller than. Can the partially observed matrix be recovered and under what kind of conditions such a matrix can be exactly recovered?

EXAMPLES OF IMPOSSIBLE RECOVERY This matrix can not be recovered unless all of the entries are given. Reason: for most sampling sets, only observing all of zeros. Not all of the matrices can be completed from a sample of their entries.

EXAMPLES OF IMPOSSIBLE RECOVERY The observation does not include samples from first row, the first component could never be guessed out. Not all the sampling set can be used to complete the matrix.

SHORT CONCLUSION One can not recover all low-rank matrices from any set of sampled entries. Can one recover most matrices from almost all sampling sets of cardinality ? The two theorems given later will tell that this is possible for most low-rank matrices under some specific conditions.

ALGORITHM Intuitively, (NP-hard problem) Locations of observed entries Alternatively, considering a heuristic optimization in which Sum of singular values Is (1. 5) reasonable or to what extent it is equivalent to rank minimization?

THE FIRST THEOREM Talk later There is unique low-rank matrix consistent with the observed entries. The heuristic model (1. 5) is equivalent to the above NP-hard formulation.

RANDOM ORTHOGONAL MODEL Generic low-rank matrix SVD (singular value decomposition ) of a matrix

A DEFINITION The subspace with low coherence is the special interest of this paper. Singular vectors with low coherence is “spread out. ”(not sparse) It can guarantee that the sampling set cannot really be a zero set.

TWO ASSUMPTIONS

MAIN RESULTS Theorem 1. 1 is a special case of theorem 1. 3. If only a few matrices satisfy the conditions, it will also make theorem 1. 3 of little practical use.

THE CONDITIONS OF THEOREM 1. 3 The random orthogonal model obeys the two assumptions A 0 and A 1 with large probability.

THE PROOF OF THE LEMMAS

REVIEW OF THEOREM 1. 3

THE PROOF The author employs the tools of subgradient (in distributions (generalized functional) and duality ( in optimization theory) and tools in asymptotic geometric analysis to prove the existence and uniqueness of theorem (1. 3). The proof is from page. 15 -42. The details won’t be discussed here.

DUALITY(1) In optimization theory, the duality principle states that optimization problems may be viewed from either of two perspectives, the primal problem or the dual problem. (Wikipedia) Concept in constraint optimization

DUALITY(2) The largest singular value

DUALITY(3) in which Orthogonal complement

DUALITY(4) Ensure Y is the subgradient of nuclear norm at X 0 Property of injectivity Equivalent to the operator

ARCHITECTURE OF THE PROOF(1) The candidate Y which vanishes on the complement of the will be the solution to the optimization model of

ARCHITECTURE OF THE PROOF(2) The candidate Y which vanishes on the complement of the will be the solution to Hopefully, the small Frobenius norm will indicate the small spectral norm as well. Prove the first statement The first part of the statement 1.

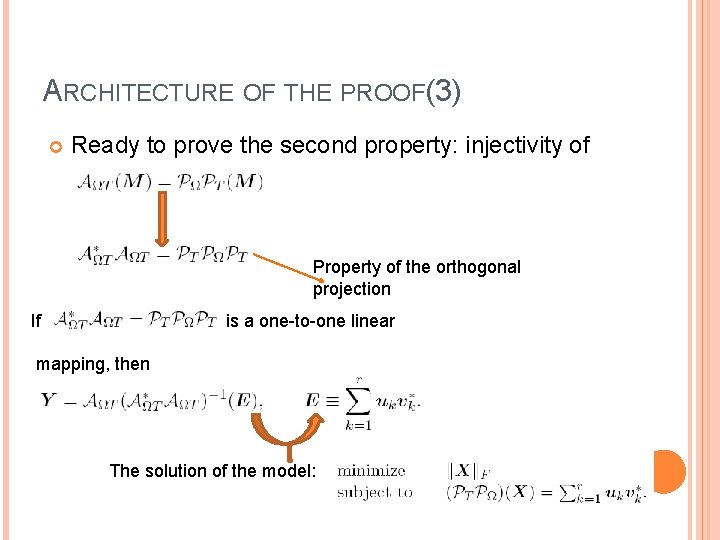
ARCHITECTURE OF THE PROOF(3) Ready to prove the second property: injectivity of Property of the orthogonal projection If is a one-to-one linear mapping, then The solution of the model:

ARCHITECTURE OF THE PROOF(4) Bernoulli model of the sampling set

ARCHITECTURE OF THE PROOF(5)

ARCHITECTURE OF THE PROOF(6)

CONNECTIONS TO TRACE HEURISTIC When the matrix variable is symmetric and positive semidefinite: Which is equivalent to

EXTENSIONS The matrix completion can be extended to multitask and multiclass learning problems in machine learning.

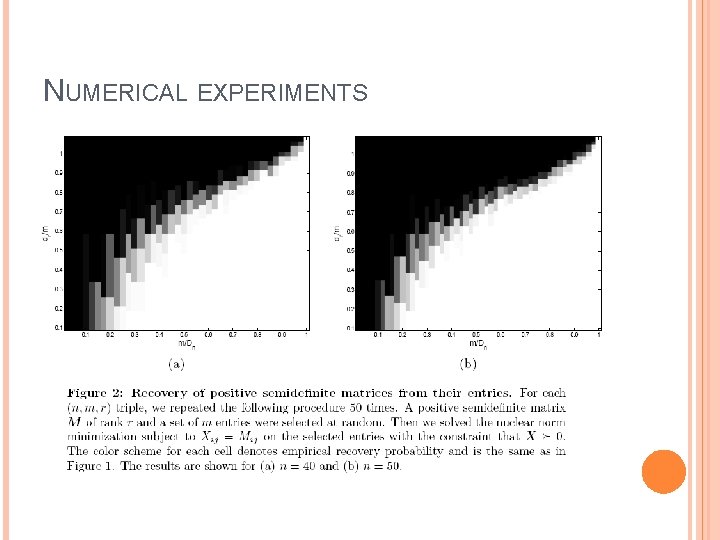
NUMERICAL EXPERIMENTS

NUMERICAL EXPERIMENTS

NUMERICAL RESULTS

DISCUSSIONS Under suitable conditions, the matrix can be completed for a small number of the sampled entries. The required number of the sample entries is on the order of.

Questions? Thank you!
 Exact matrix completion via convex optimization
Exact matrix completion via convex optimization Convex and non convex polygon examples
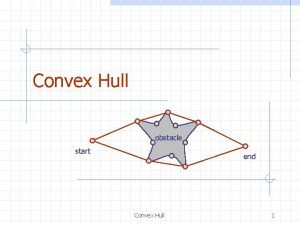
Convex and non convex polygon examples Convex hull is the smallest convex set
Convex hull is the smallest convex set Convex optimization in machine learning javatpoint
Convex optimization in machine learning javatpoint Convex optimization
Convex optimization Lions epfl
Lions epfl Imágenes de las 1-4 estaciones del vía lucis
Imágenes de las 1-4 estaciones del vía lucis Rodete piramidal
Rodete piramidal Decimo quinta estacion via crucis
Decimo quinta estacion via crucis Via erudita e via popular
Via erudita e via popular Via negativa
Via negativa Matrix multiplication cache optimization
Matrix multiplication cache optimization Cuda matrix multiplication optimization
Cuda matrix multiplication optimization Emmanuel dudognon
Emmanuel dudognon Avareza emmanuel
Avareza emmanuel Emmanuel cordonnier
Emmanuel cordonnier Emmanuel bert
Emmanuel bert Llamar emmanuel
Llamar emmanuel Emmanuel garant peintre
Emmanuel garant peintre Emmanuel boutillon
Emmanuel boutillon Emmanuel tsesmelis
Emmanuel tsesmelis Emmanuel kant la musique est la langue des émotions
Emmanuel kant la musique est la langue des émotions Emmanuel beam
Emmanuel beam Emmanuel dard
Emmanuel dard O jugo leve emmanuel
O jugo leve emmanuel Quel beau nom que celui d'emmanuel
Quel beau nom que celui d'emmanuel Emmanuel bertin
Emmanuel bertin Berkeley international office advising
Berkeley international office advising Emmanuel mondon
Emmanuel mondon Navigation atpl
Navigation atpl Bem aventurados os puros de coração espiritismo
Bem aventurados os puros de coração espiritismo A verdadeira propriedade emmanuel
A verdadeira propriedade emmanuel Emmanuel agu
Emmanuel agu Emmanuel monod
Emmanuel monod Smiologie
Smiologie