Percentage Percentage Percentage Find each amount a 12





















































- Slides: 53

Percentage

Percentage

Percentage Find each amount. a) 12% of 40 c) 5% of 320 m e) 4. 5% of 20 kg g) 90% of 45 g b) 18% of $36. 00 d) 21. 5% of 2500 f) 7. 5% of 360˚ h) 36% of $5. 50

Percentage Find each percent. a) 40 out of 200 b) 75 g out of 225 g c) 64 out of 16 d) 32 out of 180 e) 21 out of 100 f) 12 out of 8

Word Problem 1. Fred earned $325 last year working at the Pizza Boat. He spent $165. What percent of his money did he spend? 2. There are 1970 students in the school, 550 of which are grade 9 students. What percent of students are in grade 9. What percent of students are NOT in grade 9.

DISCOUNT AND SALES TAX


Outline: • Ratios! What is a Ratio? How to Use Ratios? How to Simplify? Proportions! What is a proportion? Properties of proportions? How to use proportions? • Mysterious Problems…

Ratios and Proportions

Outline: • Ratios! What is a Ratio? How to Use Ratios? How to Simplify? Proportions! What is a proportion? Properties of proportions? How to use proportions? • Mysterious Problems…

What is a Ratio? • A ratio is a comparison of two numbers. • Ratios can be written in three different ways: a to b a: b Because a ratio is a fraction, b can not be zero Ratios are expressed in simplest form

How to Use Ratios? • The ratio of boys and girls in the class is 12 to 11. This means, for every 12 boys you can find 11 girls to match. How could manybe dogs cats do • There justand 12 boys, 11 I have? We don’t know, all we girls. knowcould is if they’d fight, • There be 24 start boys, a 22 girls. eachcould dog has to fight 2 cats. • There be 120 boys, 110 4 cm girls…a huge class 1 cm • The ratio of length and width of this rectangle is 4 to 1. What is the ratio if the rectangle is 8 cm long and 2 cm wide? Still 4 to 1, because for every 4 cm, you can find 1 cm to match . • The ratio of cats and dogs at my home is 2 to 1

How to simplify ratios? • The ratios we saw on last slide were all simplified. How was it done? Ratios can be expressed The ratio of boys and girls in the class is The ratio of the rectangle is in fraction form… This allows us to do math on them. The ratio of cats and dogs in my house is

How to simplify ratios? • Now I tell you I have 12 cats and 6 dogs. Can you simplify the ratio of cats and dogs to 2 to 1? = = Divide both numerator and denominator by their Greatest Common Factor 6.

How to simplify ratios? A person’s arm is 80 cm, he is 2 m tall. Find the ratio of the length of his arm to his total height To compare them, we need to convert both numbers into the same unit …either cm or m. • Let’s try cm first! Once we have the same units, we can simplify them.

How to simplify ratios? • Let’s try m now! Once we have the same units, they simplify to 1. To make both numbers integers, we multiplied both numerator and denominator by 10

How to simplify ratios? • If the numerator and denominator do not have the same units it may be easier to convert to the smaller unit so we don’t have to work with decimals… 3 cm/12 m = 3 cm/1200 cm = 1/400 2 kg/15 g = 2000 g/15 g = 400/3 5 ft/70 in = (5*12)in / 70 in = 60 in/70 in = 6/7 2 g/8 g = 1/4 Of course, if they are already in the same units, we don’t have to worry about converting. Good deal

More examples… = = =

Now, on to proportions! What is a proportion? A proportion is an equation that equates two ratios The ratio of dogs and cats was 3/2 The ratio of dogs and cats now is 6/4=3/2 So we have a proportion :

Properties of a proportion? Cross Product Property 2 x 6=12 3 x 4 = 2 x 6

Properties of a proportion? • Cross Product Property ad = bc means extremes

Properties of a proportion? Let’s make sense of the Cross Product Property… For any numbers a, b, c, d:

Properties of a proportion? • Reciprocal Property If Then Can you see it? If yes, can you think of why it works?

How about an example? Solve for x: 7(6) = 2 x 42 = 2 x 21 = x Cross Product Property

How about another example? Solve for x: 7 x = 2(12) Cross Product Property 7 x = 24 x= Can you solve it using Reciprocal Property? If yes, would it be easier?

Can you solve this one? Solve for x: 7 x = (x-1)3 Cross Product Property 7 x = 3 x – 3 4 x = -3 x= Again, Reciprocal Property?

Now you know enough about properties, let’s solve the Mysterious problems! If your car gets 30 miles/gallon, how many gallons of gas do you need to commute to school everyday? 5 miles to home 5 miles to school Let x be the number gallons we need for a day: x= Gal Can you solve it from here?

5 miles to home 5 miles to school So you use up 1/3 gallon a day. How many gallons would you use for a week? Let t be the number of gallons we need for a week: What property is this? Gal

So you use up 5/3 gallons a week (which is about 1. 67 gallons). Consider if the price of gas is 3. 69 dollars/gal, how much would it cost for a week? Let s be the sum of cost for a week: 3. 69(1. 67) = 1 s s = 6. 16 dollars 5 miles to home 5 miles to school

So what do you think? 5 miles 10 miles You pay about 6 bucks a week just to get to school! What about weekends? If you travel twice as much on weekends, say drive 10 miles to the Mall and 10 miles back, how many gallons do you need now? How much would it cost totally? How much would it cost for a month? Think proportionally!. . . It’s all about proportions!

Geometric Relationships

Classify Polygons Polygon – is a closed figure formed by three or more line segments Regular polygon – has all sides equal and all angles equal Regular quadrilateral is a square. An irregular quadrilateral may be a rectangle, a rhombus, a parallelogram, or a trapezoid.

Regular quadrilateral

Regular and Irregular quadrilateral

Angle Properties • When two lines intersect , the opposites angles are equal

• The sum of the interior angles of a triangle is 180 degree.

What is x?

Alternate angles are equal

Corresponding angles are equal

Co-interior angles have a sum of 180 degree

Angle Relationships in Triangles • Vertex – point where two or more sides meet

• Interior angle – angle formed on the inside of a polygon by two sides meeting at a vertex • Exterior angle – angle formed on the outside of a geometric shape by extending one of the sides past a vertex

Find the measure of the exterior angles of ABC

Find a, b, and c.

Exterior Angles of a triangle • The sum of the exterior angles of a triangle is 360 degree.

Angle Relationship is Quadrilaterals • Sum of interior angles of a quadrilateral is 360 degree

Angle Relationship of Quadrilateral • Sum or the exterior angles of a quadrilateral

Angle Relationships in Parallelograms • Adjacent – adjoining or next to • Supplementary – adding to 180 degree • Transversal – line intersecting two or more lines

Angle Relationships in Polygons • Convex polygon – a polygon with no part of any line segment joining two points on the polygon outside the polygon • Concave polygon – a polygon with parts of some line segments joining two points on the polygon outside the polygon

Polygons • • • Pentagon – a polygon with five sides Hexagon – a polygon with six sides Heptagon – a polygon with seven sides Octagon – a polygon with eight sides Regular polygon – a polygon with all sides equal and all interior angles equal SUM OF INTERIOR ANGLES = 180(n-2)

Polygons

REMEMBER

Midpoints and Medians in Triangles • Midpoint – the point that divides a line segment into two equal segments
 How to read centavos
How to read centavos ब्याज का सूत्र
ब्याज का सूत्र P= i/rt
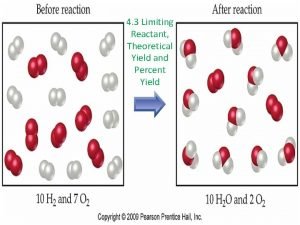
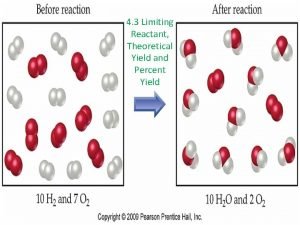
P= i/rt How do you find how much excess reactant is left over
How do you find how much excess reactant is left over How to calculate percent composition by mass
How to calculate percent composition by mass Use the properties of exponents to rewrite each expression
Use the properties of exponents to rewrite each expression Identify each line or segment that intersects each circle
Identify each line or segment that intersects each circle Percent strength w/v
Percent strength w/v Means out of 100
Means out of 100 How to find percentage decrease
How to find percentage decrease How to find percentage yeild
How to find percentage yeild How to find decreasing percentage
How to find decreasing percentage Find percentage increase
Find percentage increase Percentage decrease calculator
Percentage decrease calculator How to find the percent increase
How to find the percent increase Percent composition by mass
Percent composition by mass How to get percentage decrease
How to get percentage decrease How to get the selling price
How to get the selling price How to find percentage decrease
How to find percentage decrease How to find percentage decrease
How to find percentage decrease Percent yoeld
Percent yoeld How to find theoretical yield
How to find theoretical yield Definition of percent composition
Definition of percent composition 582 x 4
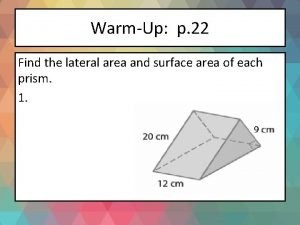
582 x 4 Perimeter and area of complex figures
Perimeter and area of complex figures How to find inscribed angles
How to find inscribed angles Find the measure of each angle
Find the measure of each angle Find the inverse for each relation
Find the inverse for each relation Find the radius and diameter of each circle
Find the radius and diameter of each circle Find the odd one out brother sister mother grandson
Find the odd one out brother sister mother grandson In the figure, m∠7 = 100° . find the measure of ∠9 .
In the figure, m∠7 = 100° . find the measure of ∠9 . Find the area of each shape
Find the area of each shape Area of segment example
Area of segment example Find volum
Find volum Find the value of each variable
Find the value of each variable Find x
Find x Multiplying polynomials find each product
Multiplying polynomials find each product Quadrilateral rstq is a parallelogram
Quadrilateral rstq is a parallelogram Factors of 5 and 3
Factors of 5 and 3 Lesson 5-4 the triangle midsegment theorem
Lesson 5-4 the triangle midsegment theorem Lesson 8: solve for unknown angles—angles in a triangle
Lesson 8: solve for unknown angles—angles in a triangle Find each root
Find each root 5-1 geometry
5-1 geometry Lesson 25-3 multiplying polynomials
Lesson 25-3 multiplying polynomials Find the area of each rhombus
Find the area of each rhombus Find the volume of each pyramid
Find the volume of each pyramid Lateral edge
Lateral edge Find each measure
Find each measure Find the area of each figure
Find the area of each figure Find m
Find m Composite solid
Composite solid L x w x h
L x w x h Volume of prism and cylinder
Volume of prism and cylinder Find each indicated measure
Find each indicated measure