z Concept 52 3 D Shapes Polyhedron Solid











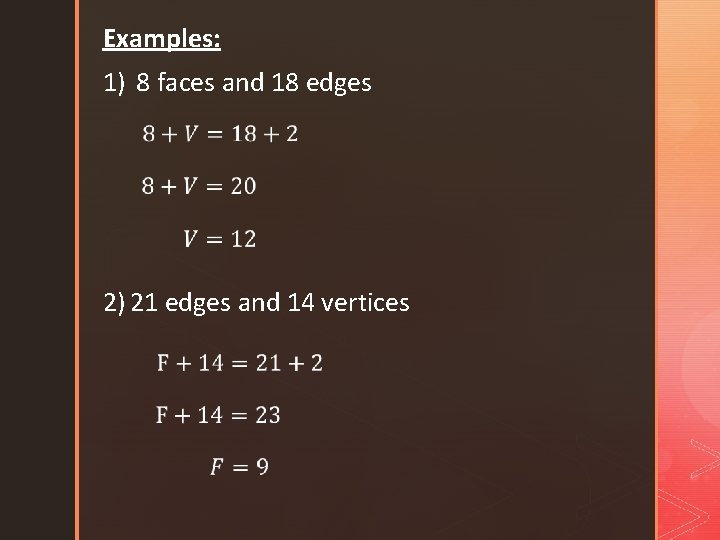













- Slides: 54

z Concept 52 3 -D Shapes

Polyhedron Solid Convex Concave Regular Cylinder Prism Cone Pyramid Sphere

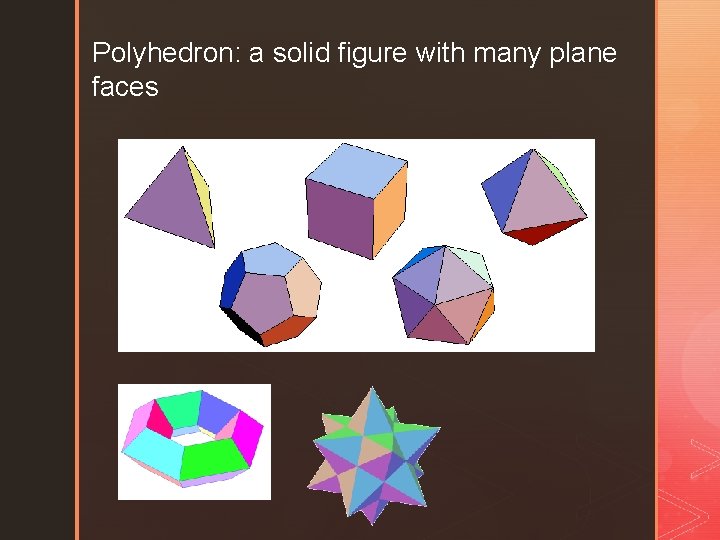
Polyhedron: a solid figure with many plane faces

Solid: a 3 -D shape that encloses space but is not made up of all polygon sides.

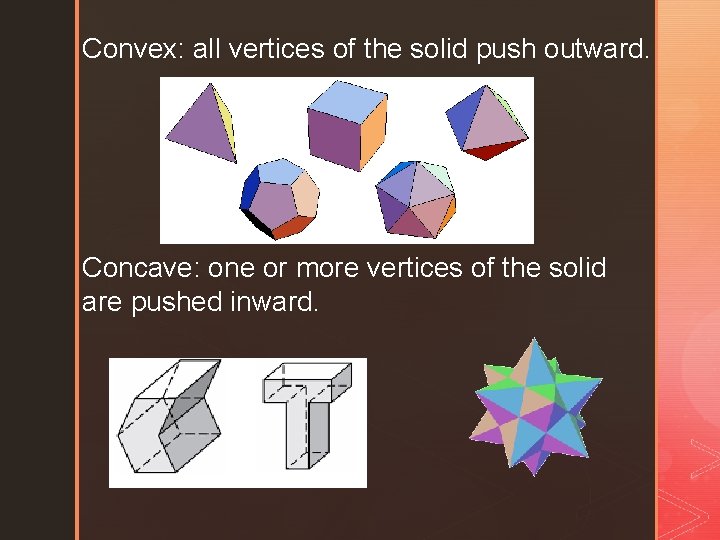
Convex: all vertices of the solid push outward. Concave: one or more vertices of the solid are pushed inward.

Regular: a polyhedron with all the same regular polygons.

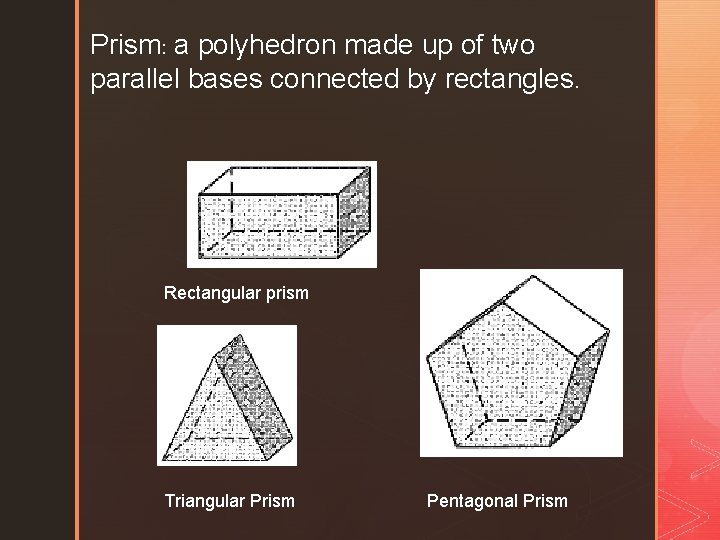
Prism: a polyhedron made up of two parallel bases connected by rectangles. Rectangular prism Triangular Prism Pentagonal Prism

Pyramid:

Cylinder:

Cone:

Sphere:

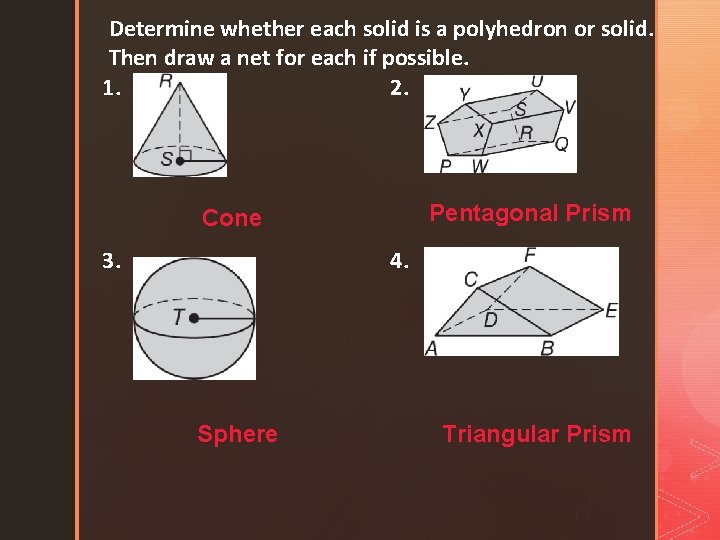
Determine whether each solid is a polyhedron or solid. Then draw a net for each if possible. 1. 2. Pentagonal Prism Cone 3. 4. Sphere Triangular Prism

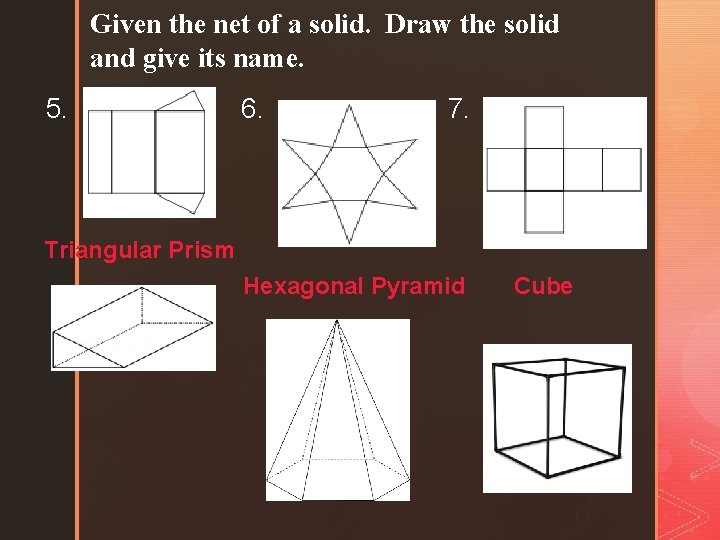
Given the net of a solid. Draw the solid and give its name. 5. 6. 7. Triangular Prism Hexagonal Pyramid Cube

z Concept 53 Parts of Solids and Cross Section

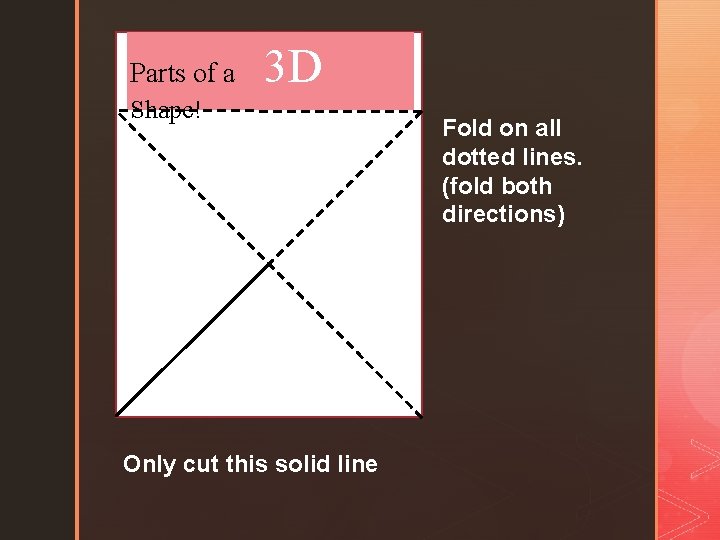
Parts of a 3 D Shape! Only cut this solid line Fold on all dotted lines. (fold both directions)

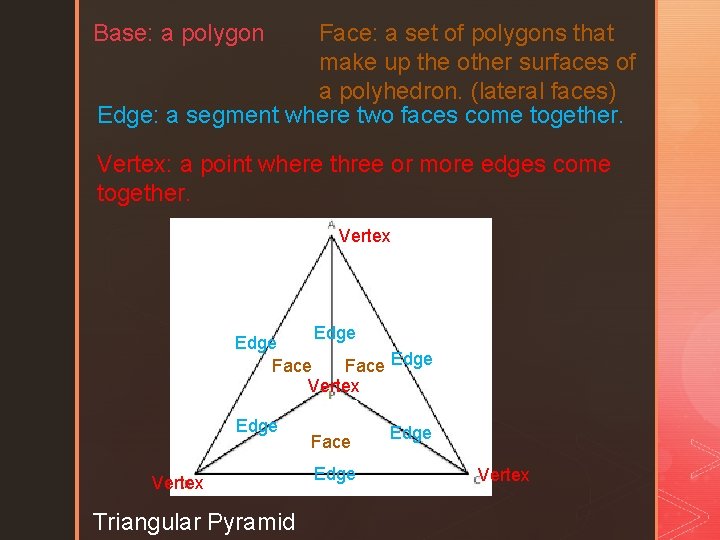
Face: a set of polygons that make up the other surfaces of a polyhedron. (lateral faces) Edge: a segment where two faces come together. Base: a polygon Vertex: a point where three or more edges come together. Vertex Edge Face Edge Vertex Base: Edge Face Vertex Triangular Pyramid Edge Vertex

Then identify the solid. If it is a polyhedron, name the faces, edges, and vertices. 9. 10. Faces: Circle S (B) Edges: none Vertices: Point R Faces: Pentagons: PWXYX and QRSUV, Quadrilaterals: QVXW, UVXY, USZY, PRSZ, PRXW Edges: Vertices: Points: P, W, X, Y, Z, Q, R, S, U, V

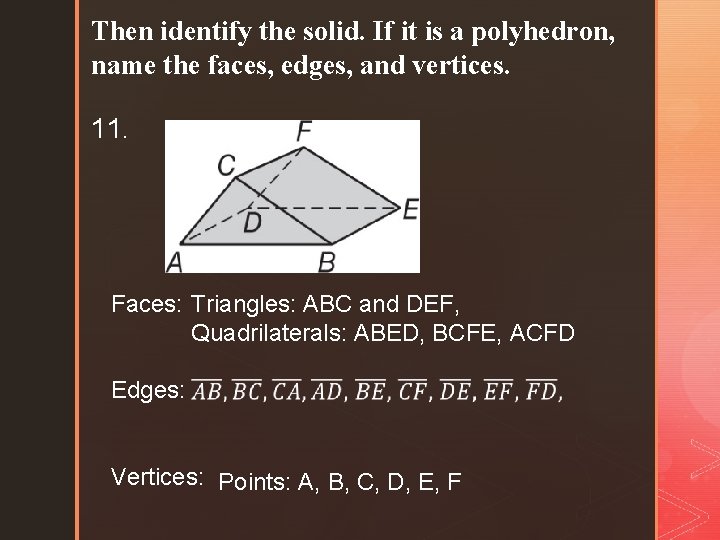
Then identify the solid. If it is a polyhedron, name the faces, edges, and vertices. 11. Faces: Triangles: ABC and DEF, Quadrilaterals: ABED, BCFE, ACFD Edges: Vertices: Points: A, B, C, D, E, F

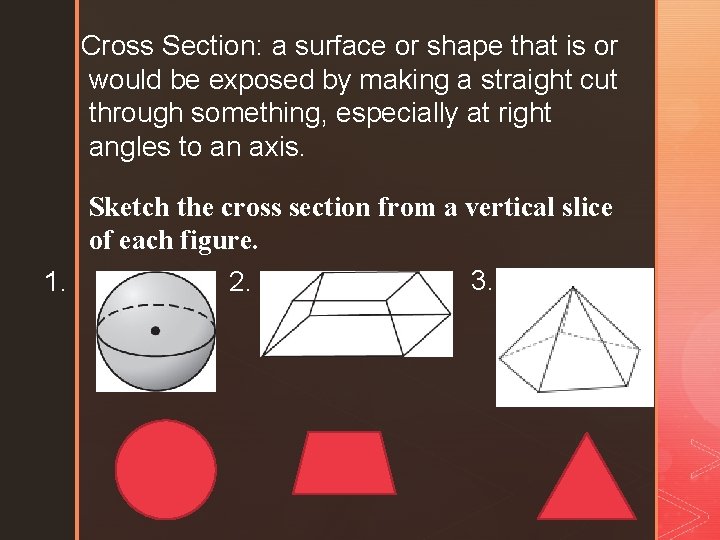
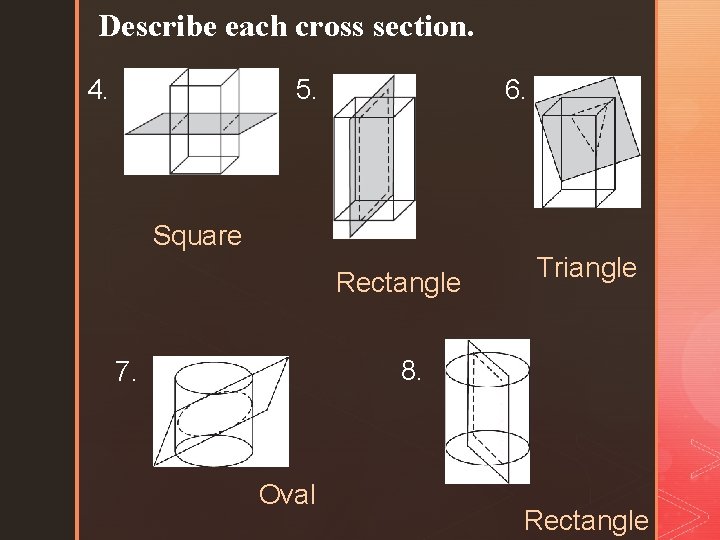
a surface or shape that is or Cross Section: would be exposed by making a straight cut through something, especially at right angles to an axis. Sketch the cross section from a vertical slice of each figure. 3. 1. 2.

Describe each cross section. 4. 5. 6. Square Rectangle Triangle 8. 7. Oval Rectangle


z Concept 54 Euler’s Theorem

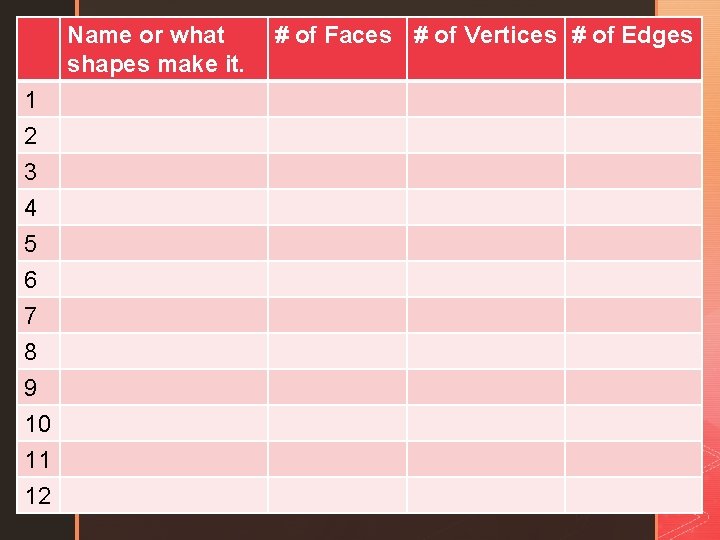
There are 11 polyhedrons located around the room at each group of desks. Use each one to fill in a row of the table. If the shape has a name you know write it in the first column, otherwise just write what it is made up of. Ex. (2 triangles and 3 rectangles)

Name or what shapes make it. 1 2 3 4 5 6 7 8 9 10 11 12 # of Faces # of Vertices # of Edges

Euler’s Theorem F+V=E+2
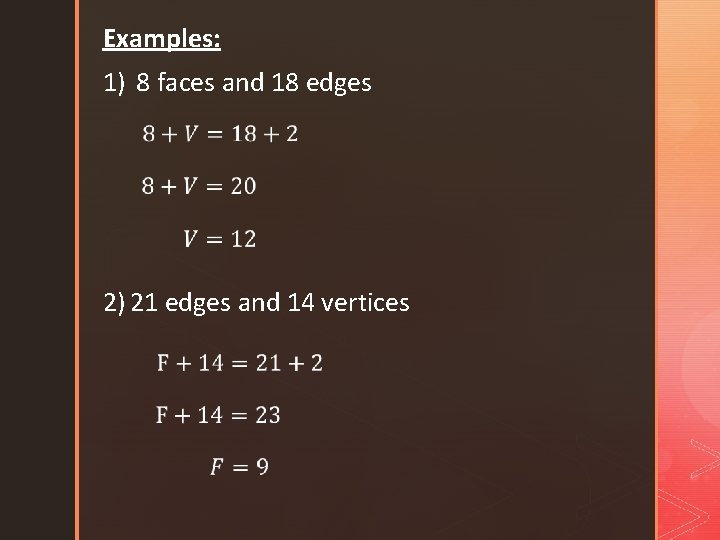
Examples: 1) 8 faces and 18 edges 2) 21 edges and 14 vertices

3) 12 pentagon faces 4) 8 triangle faces 5) 1 hexagon and 6 triangle faces

6) 20 triangle faces 7) 12 pentagon and 20 hexagon faces

2 hexagons and 6 rectangles

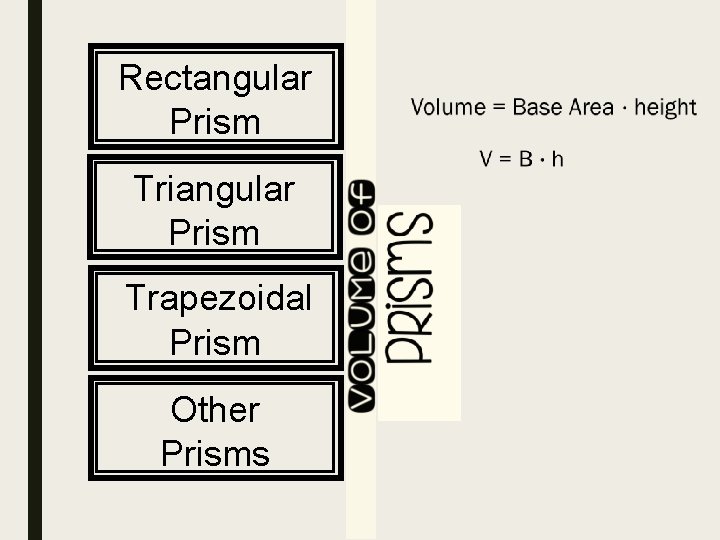
VOLUME OF PRISMS Concept 55

Rectangular Prism Triangular Prism Trapezoidal Prism Other Prisms

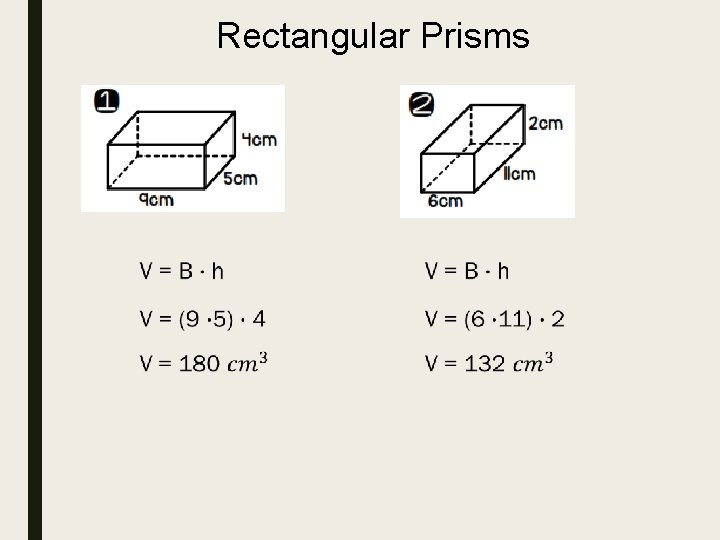
Rectangular Prisms

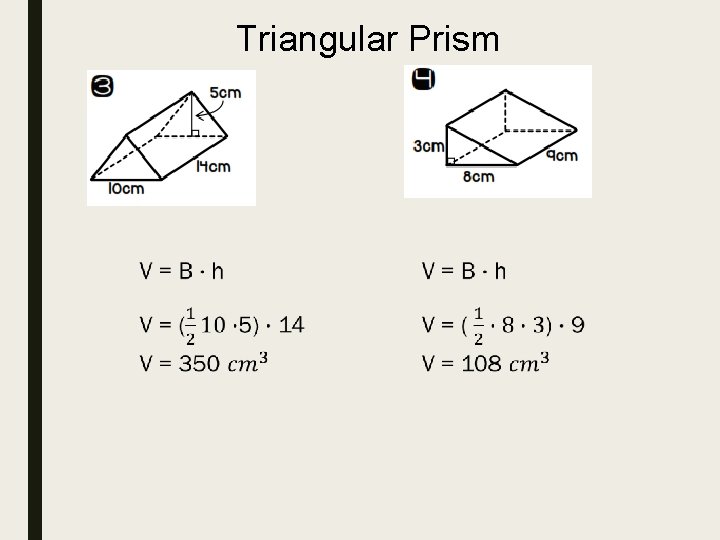
Triangular Prism

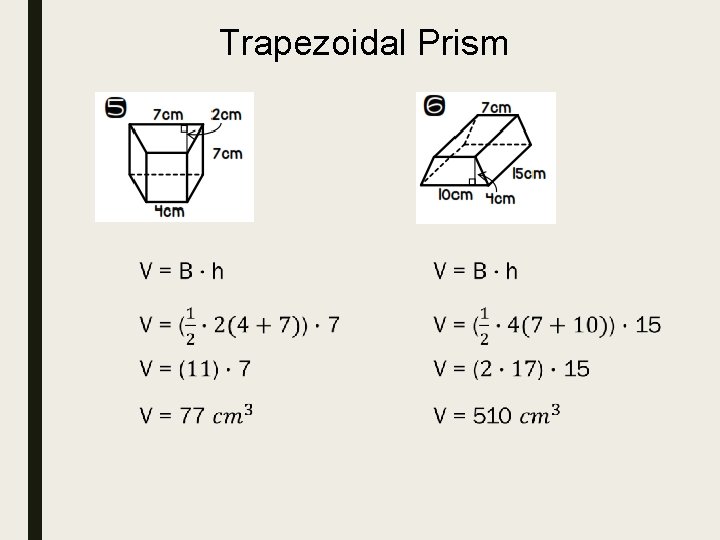
Trapezoidal Prism

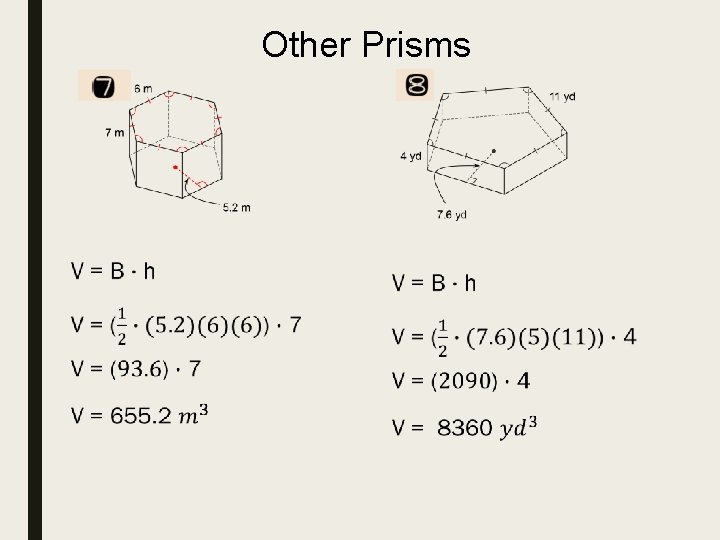
Other Prisms

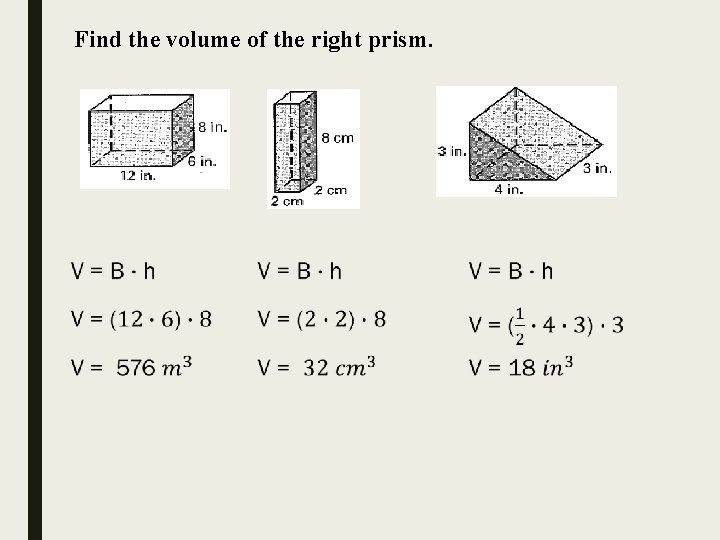
Find the volume of the right prism.

Find the missing side length given the Volume, V of each solid. 4. V = 480 cm 2 5. V = 120 in 2 6. V = 180 cm 2 480 = 96 x 120 = 10 x 180 =10(x +12) 5 cm = x 12 in = x 18 = x + 12 6 cm = x

VOLUME OF PYRAMIDS Concept 56

Volume of Pyramids Square Pyramid Triangular Pyramid Other Pyramids

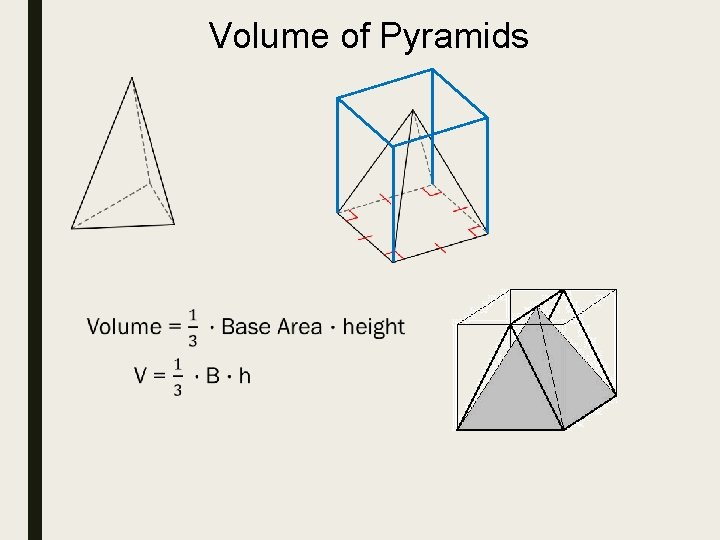
Volume of Pyramids

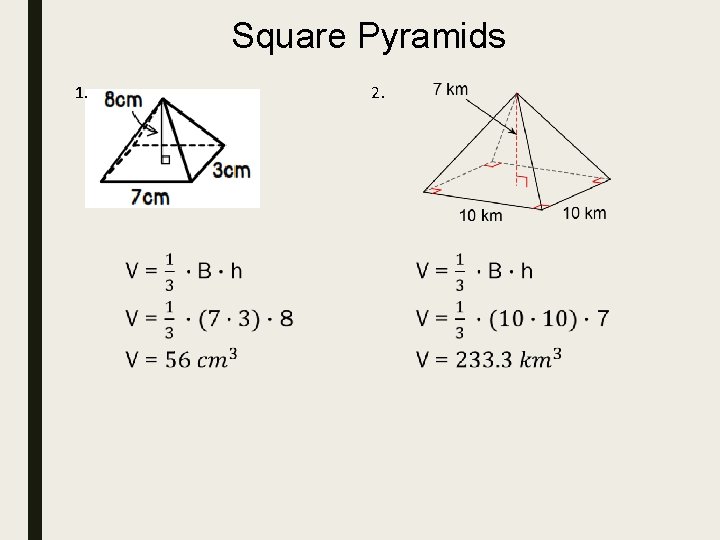
Square Pyramids 2. 1.

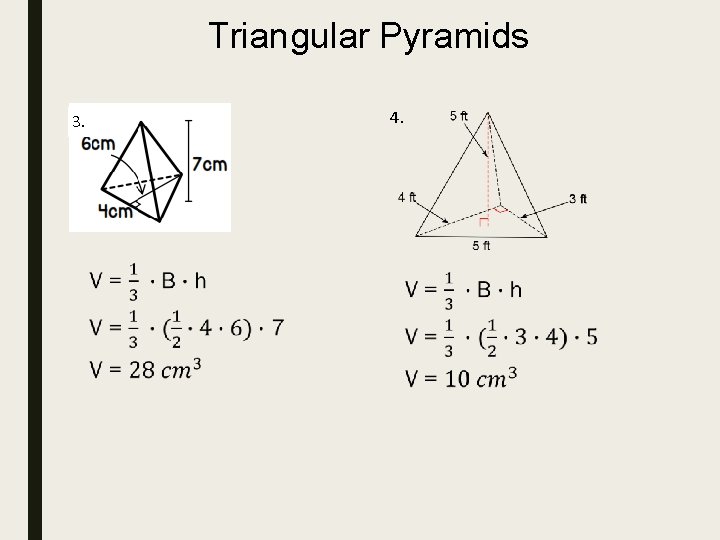
Triangular Pyramids 4. 3.

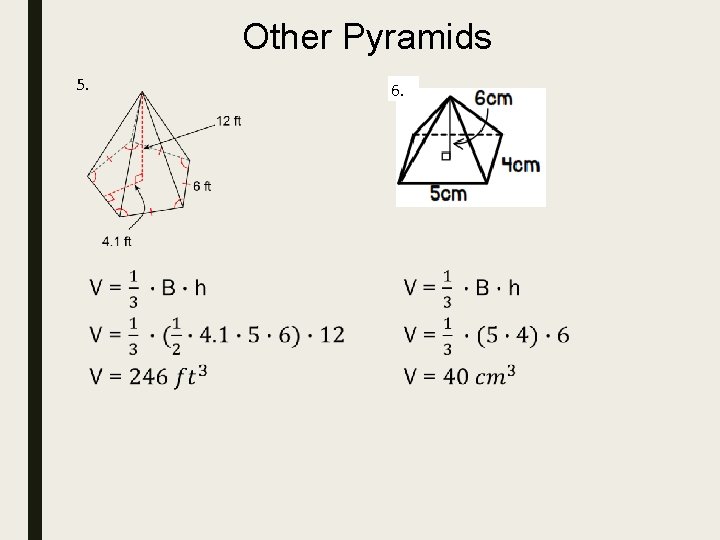
Other Pyramids 5. 6.

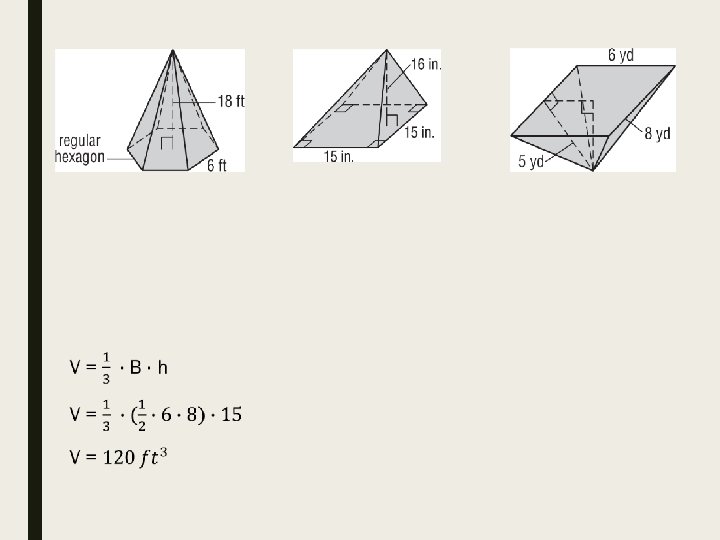
Find the volume of each pyramid. Round to the nearest tenth if necessary.


VOLUME OF CYLINDERS, CONES, AND SPHERES Concepts 57 - 59






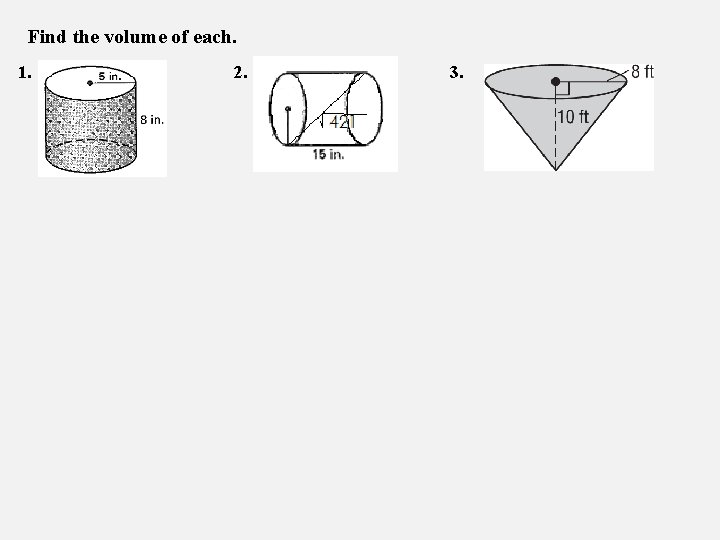
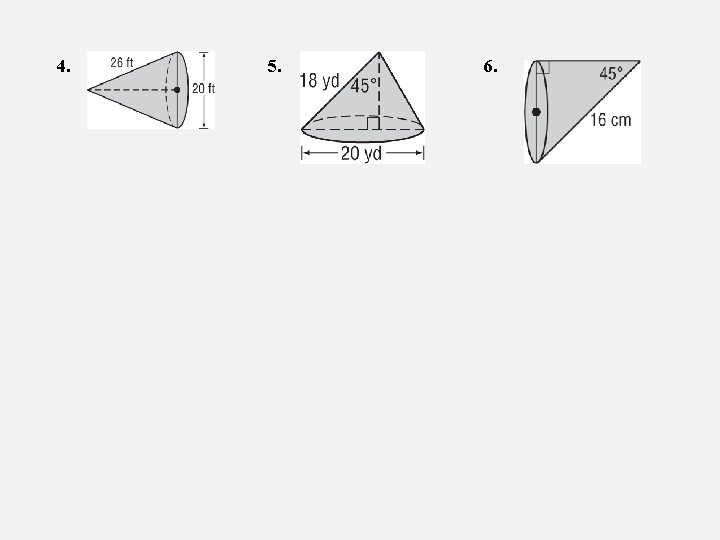
Find the volume of each. 1. 2. 3.

4. 5. 6.

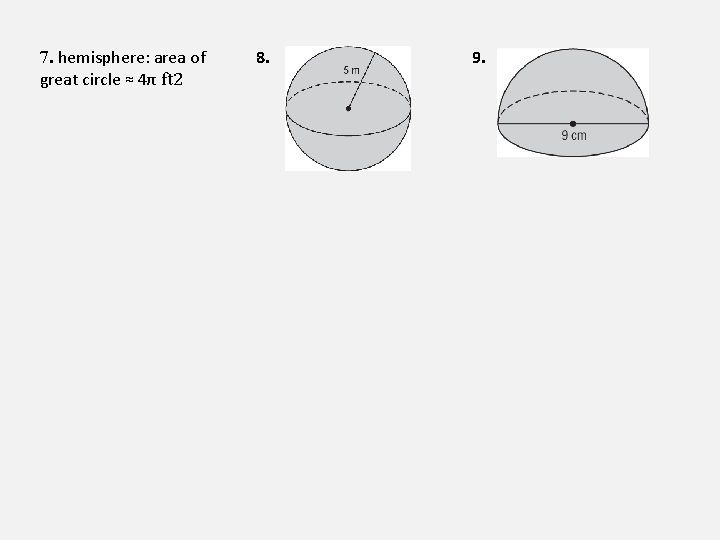
7. hemisphere: area of great circle ≈ 4π ft 2 8. 9.