Percentages Questions and Answers Fractions Decimals and Percentages

Percentages Questions and Answers • Fractions, Decimals and Percentages • Finding Percentages • Percentage Increase/Decrease • Reverse Percentages • You tube playlist LINK

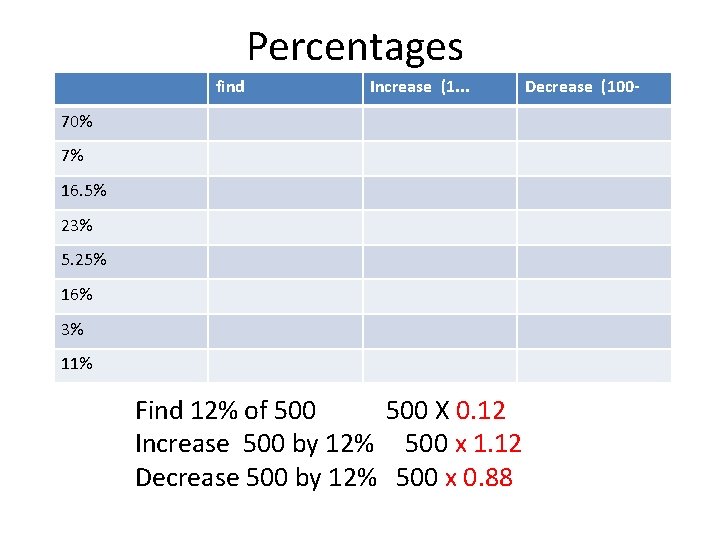
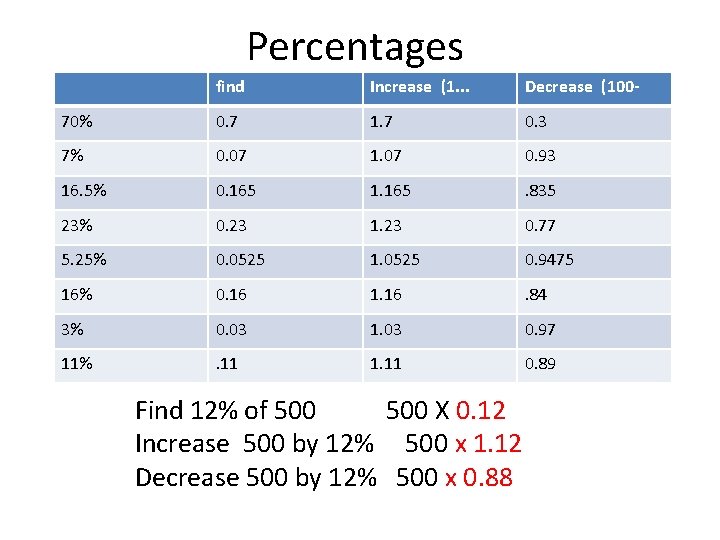
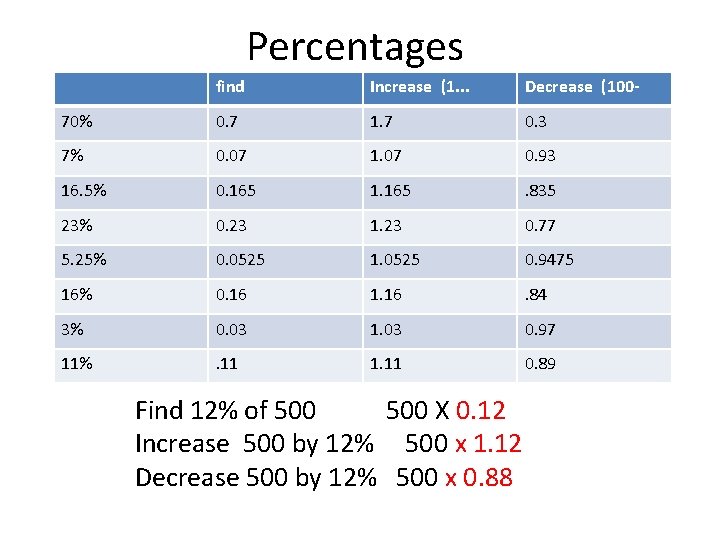
Percentages find Increase (1. . . 70% 7% 16. 5% 23% 5. 25% 16% 3% 11% Find 12% of 500 X 0. 12 Increase 500 by 12% 500 x 1. 12 Decrease 500 by 12% 500 x 0. 88 Decrease (100 -

Percentages find Increase (1. . . Decrease (100 - 70% 0. 7 1. 7 0. 3 7% 0. 07 1. 07 0. 93 16. 5% 0. 165 1. 165 . 835 23% 0. 23 1. 23 0. 77 5. 25% 0. 0525 1. 0525 0. 9475 16% 0. 16 1. 16 . 84 3% 0. 03 1. 03 0. 97 11% . 11 1. 11 0. 89 Find 12% of 500 X 0. 12 Increase 500 by 12% 500 x 1. 12 Decrease 500 by 12% 500 x 0. 88

Contents N 5 Percentages N 5. 1 Fractions, decimals and percentages N 5. 2 Percentages of quantities N 5. 3 Finding a percentage change N 5. 4 Increasing and decreasing by a percentage N 5. 5 Reverse percentages N 5. 6 Compound percentages

Percentage increase The value of Frank’s house has gone up by 20% since last year. If the house was worth £ 150 000 last year how much is it worth now? There are two methods to increase an amount by a given percentage. Method 1 We can work out 20% of £ 150 000 and then add this to the original amount. The amount of the increase = 20% of £ 150 000 = 0. 2 × £ 150 000 = £ 30 000 The new value = £ 150 000 + £ 30 000 = £ 180 000

Percentage increase Method 2 If we don’t need to know the actual value of the increase we can find the result in a single calculation. We can represent the original amount as 100% like this: 100% When we add on 20%, 20% we have 120% of the original amount. Finding 120% of the original amount is equivalent to finding 20% and adding it on.

Percentage increase So, to increase £ 150 000 by 20% we need to find 120% of £ 150 000 = 1. 2 × £ 150 000 = £ 180 000 In general, if you start with a given amount (100%) and you increase it by x%, then you will end up with (100 + x)% of the original amount. To convert (100 + x)% to a decimal multiplier we have to divide (100 + x) by 100. This is usually done mentally.

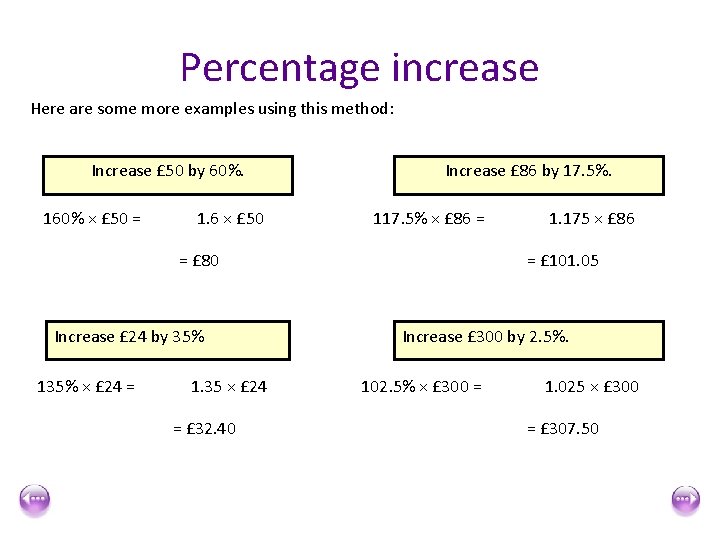
Percentage increase Here are some more examples using this method: Increase £ 50 by 60%. 160% × £ 50 = 1. 6 × £ 50 Increase £ 86 by 17. 5%. 117. 5% × £ 86 = = £ 80 Increase £ 24 by 35% 135% × £ 24 = 1. 35 × £ 24 = £ 32. 40 1. 175 × £ 86 = £ 101. 05 Increase £ 300 by 2. 5%. 102. 5% × £ 300 = 1. 025 × £ 300 = £ 307. 50

Percentage decrease A CD walkman originally costing £ 75 is reduced by 30% in a sale. What is the sale price? There are two methods to decrease an amount by a given percentage. Method 1 We can work out 30% of £ 75 and then subtract this from the original amount. The amount taken off = 30% of £ 75 = 0. 3 × £ 75 = £ 22. 50 The sale price = £ 75 – £ 22. 50 = £ 52. 50

Percentage decrease Method 2 We can use this method to find the result of a percentage decrease in a single calculation. We can represent the original amount as 100% like this: 70% When we subtract 30% 100% 30% we have 70% of the original amount. Finding 70% of the original amount is equivalent to finding 30% and subtracting it.

Percentage decrease So, to decrease £ 75 by 30% we need to find 70% of £ 75 = 0. 7 × £ 75 = £ 52. 50 In general, if you start with a given amount (100%) and you decrease it by x%, then you will end up with (100 – x)% of the original amount. To convert (100 – x)% to a decimal multiplier we have to divide (100 – x) by 100. This is usually done mentally.

Percentage decrease Here are some more examples using this method: Decrease £ 65 by 20%. 80% × £ 65 = 0. 8 × £ 65 Decrease £ 320 by 3. 5%. 96. 5% × £ 320 = = £ 52 Decrease £ 56 by 34% 66% × £ 56 = 0. 66 × £ 56 = £ 36. 96 0. 965 × £ 320 = £ 308. 80 Decrease £ 1570 by 95%. 5% × £ 1570 = 0. 05 × £ 1570 = £ 78. 50

Percentage increase and decrease

Contents N 5 Percentages N 5. 1 Fractions, decimals and percentages N 5. 2 Percentages of quantities N 5. 3 Finding a percentage change N 5. 4 Increasing and decreasing by a percentage N 5. 5 Reverse percentages N 5. 6 Compound percentages

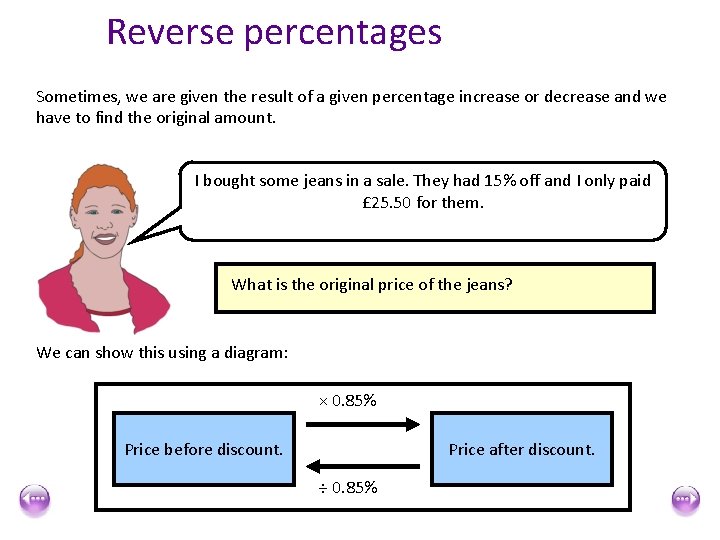
Reverse percentages Sometimes, we are given the result of a given percentage increase or decrease and we have to find the original amount. I bought some jeans in a sale. They had 15% off and I only paid £ 25. 50 for them. What is the original price of the jeans? We can solve this using inverse operations. Let p be the original price of the jeans. p × 0. 85 = £ 25. 50 so p= £ 25. 50 ÷ 0. 85 = £ 30

Reverse percentages Sometimes, we are given the result of a given percentage increase or decrease and we have to find the original amount. I bought some jeans in a sale. They had 15% off and I only paid £ 25. 50 for them. What is the original price of the jeans? We can show this using a diagram: × 0. 85% Price before discount. Price after discount. ÷ 0. 85%

Reverse percentages

Reverse percentages We can also use a unitary method to solve these type of percentage problems. For example, Christopher’s monthly salary after a 5% pay rise is £ 1312. 50. What was his original salary? The new salary represents 105% of the original salary = £ 1312. 50 1% of the original salary = £ 1312. 50 ÷ 105 100% of the original salary = £ 1312. 50 ÷ 105 × 100 = £ 1250 This method has more steps involved but may be easier to remember.

Contents N 5 Percentages N 5. 1 Fractions, decimals and percentages N 5. 2 Percentages of quantities N 5. 3 Finding a percentage change N 5. 4 Increasing and decreasing by a percentage N 5. 5 Reverse percentages N 5. 6 Compound percentages

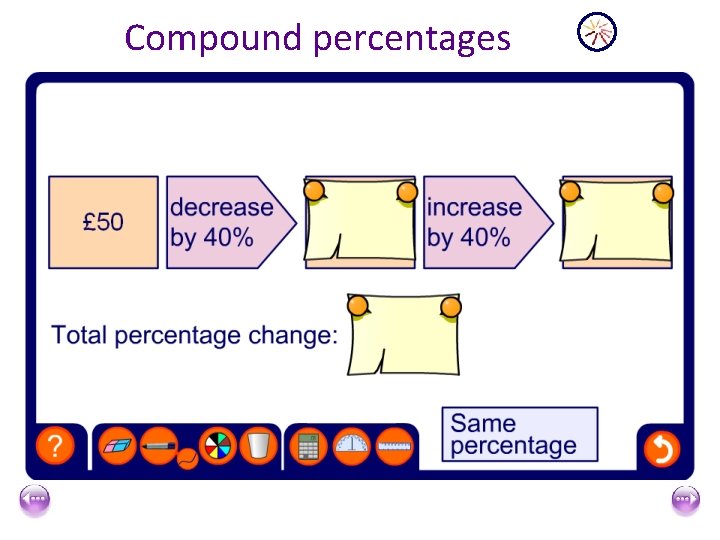
Compound percentages A jacket is reduced by 20% in a sale. Two weeks later the shop reduces the price by a further 10%. What is the total percentage discount? It is not 30%! When a percentage change is followed by another percentage change do not add the percentages together to find the total percentage change. The second percentage change is found on a new amount and not on the original amount.

Compound percentages A jacket is reduced by 20% in a sale. Two weeks later the shop reduces the price by a further 10%. What is the total percentage discount? To find a 20% decrease we multiply by 80% or 0. 8. To find a 10% decrease we multiply by 90% or 0. 9. A 20% discount followed by a 10% discount is equivalent to multiplying the original price by 0. 8 and then by 0. 9. original price × 0. 8 × 0. 9 = original price × 0. 72

Compound percentages A jacket is reduced by 20% in a sale. Two weeks later the shop reduces the price by a further 10%. What is the total percentage discount? The sale price is 72% of the original price. This is equivalent to a 28% discount. A 20% discount followed by a 10% discount A 28% discount

Compound percentages A jacket is reduced by 20% in a sale. Two weeks later the shop reduces the price by a further 10%. What is the total percentage discount? Suppose the original price of the jacket is £ 100. After a 20% discount it costs 0. 8 × £ 100 = £ 80 After an other 10% discount it costs 0. 9 × £ 80 = £ 72 is 72% of £ 100 is equivalent to a 28% discount altogether.

Compound percentages Jenna invests in some shares. After one week the value goes up by 10%. The following week they go down by 10%. Has Jenna made a loss, a gain or is she back to her original investment? To find a 10% increase we multiply by 110% or 1. 1. To find a 10% decrease we multiply by 90% or 0. 9. original amount × 1. 1 × 0. 9 = original amount × 0. 99 Fiona has 99% of her original investment and has therefore made a 1% loss.

Compound percentages

Compound interest Jack puts £ 500 into a savings account with an annual compound interest rate of 6%. How much will he have in the account at the end of 4 years if he doesn’t add or withdraw any money? At the end of each year interest is added to the total amount in the account. This means that each year 5% of an ever larger amount is added to the account. To increase the amount in the account by 5% we need to multiply it by 105% or 1. 05. We can do this for each year that the money is in the account.

Compound interest At the end of year 1 Jack has £ 500 × 1. 05 = £ 525 At the end of year 2 Jack has £ 525 × 1. 05 = £ 551. 25 At the end of year 3 Jack has £ 551. 25 × 1. 05 = £ 578. 81 At the end of year 4 Jack has £ 578. 81 × 1. 05 = £ 607. 75 (These amounts are written to the nearest penny. ) We can write this in a single calculation as £ 500 × 1. 05 = £ 607. 75 Or using index notation as £ 500 × 1. 054 = £ 607. 75

Compound interest How much would Jack have after 10 years? After 10 years the investment would be worth £ 500 × 1. 0510 = £ 814. 45 (to the nearest 1 p) How long would it take for the money to double? Using trial and improvement, £ 500 × 1. 0514 = £ 989. 97 (to the nearest 1 p) £ 500 × 1. 0515 = £ 1039. 46 (to the nearest 1 p) It would take 15 years for the money to double.

Compound interest

Repeated percentage change We can use powers to help solve many problems involving repeated percentage increase and decrease. For example, The population of a village increases by 2% each year. If the current population is 2345, what will it be in 5 years? To increase the population by 2% we multiply it by 1. 02. After 5 years the population will be 2345 × 1. 025 = 2589 (to the nearest whole) What will the population be after 10 years? After 5 years the population will be 2345 × 1. 0210 = 2859 (to the nearest whole)

Repeated percentage change The value of a new car depreciates at a rate of 15% a year. The car costs £ 24 000 in 2005. How much will it be worth in 2013? To decrease the value by 15% we multiply it by 0. 85. There are 8 years between 2005 and 2013. After 8 years the value of the car will be £ 24 000 × 0. 858 = £ 6540 (to the nearest pound)

Reverse • Bought a car 1 year ago and it has lost 45% of its value and is worth £ 3000 now, what did it cost me? • ? X. 55 = £ 3000 so ? = 3000/0. 55 = £ 5454. 55

Compound • Invest £ 5000 for 5 years earns 3% compound interest • 5000 x 1. 03^5

Percentages find Increase (1. . . Decrease (100 - 70% 0. 7 1. 7 0. 3 7% 0. 07 1. 07 0. 93 16. 5% 0. 165 1. 165 . 835 23% 0. 23 1. 23 0. 77 5. 25% 0. 0525 1. 0525 0. 9475 16% 0. 16 1. 16 . 84 3% 0. 03 1. 03 0. 97 11% . 11 1. 11 0. 89 Find 12% of 500 X 0. 12 Increase 500 by 12% 500 x 1. 12 Decrease 500 by 12% 500 x 0. 88

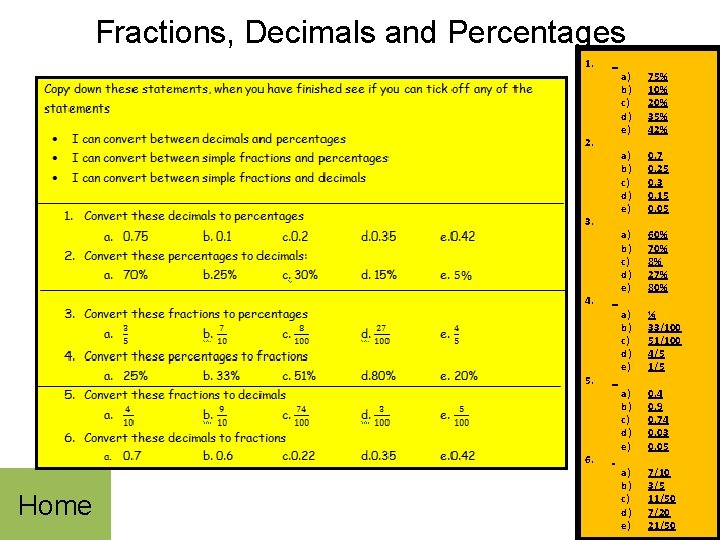
Fractions, Decimals and Percentages Home 1. 2. 3. 4. 5. 6. a) b) c) d) e) 75% 10% 20% 35% 42% a) b) c) d) e) 0. 7 0. 25 0. 3 0. 15 0. 05 a) b) c) d) e) 60% 70% 8% 27% 80% a) b) c) d) e) ¼ 33/100 51/100 4/5 1/5 a) b) c) d) e) 0. 4 0. 9 0. 74 0. 03 0. 05 a) b) c) d) e) 7/10 3/5 11/50 7/20 21/50

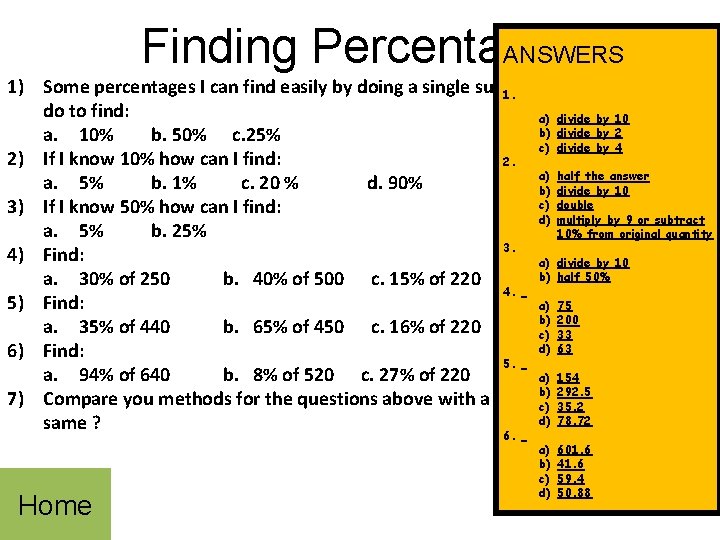
ANSWERS Finding Percentages 1) Some percentages I can find easily by doing a single sum, what single sums can I 1. do to find: a) divide by 10 b) divide by 2 a. 10% b. 50% c. 25% c) divide by 4 2) If I know 10% how can I find: 2. a) half the answer a. 5% b. 1% c. 20 % d. 90% b) divide by 10 c) double 3) If I know 50% how can I find: d) multiply by 9 or subtract a. 5% b. 25% 10% from original quantity 3. 4) Find: a) divide by 10 b) half 50% a. 30% of 250 b. 40% of 500 c. 15% of 220 d. 75% of 84 4. 5) Find: a) 75 b) 200 a. 35% of 440 b. 65% of 450 c. 16% of 220 d. 82% of 96 c) 33 d) 63 6) Find: 5. a. 94% of 640 b. 8% of 520 c. 27% of 220 d. 53% of 96 a) 154 b) 292. 5 7) Compare you methods for the questions above with a partner, where they the c) 35. 2 d) 78. 72 same ? 6. Home a) b) c) d) 601. 6 41. 6 59. 4 50. 88

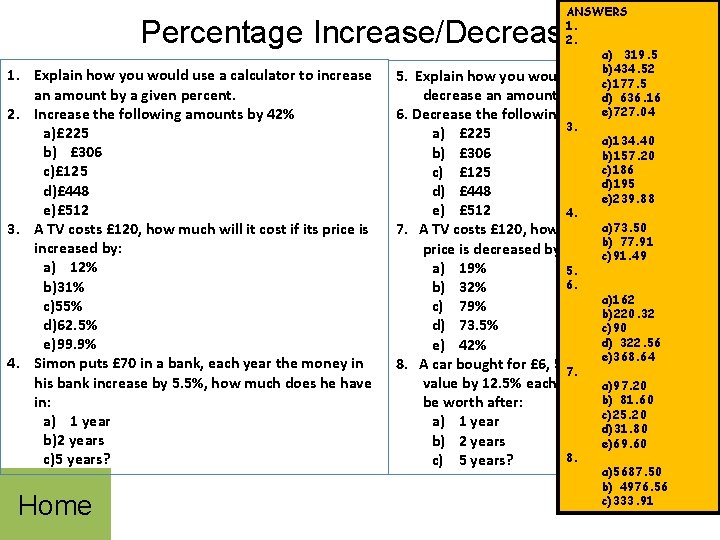
ANSWERS 1. 2. a) 319. 5 b)434. 52 5. Explain how you would use a calculator to c)177. 5 decrease an amount by a given percent. d) 636. 16 e)727. 04 6. Decrease the following amounts by 28% 3. a) £ 225 a)134. 40 b) £ 306 b)157. 20 c)186 c) £ 125 d)195 d) £ 448 e)239. 88 e) £ 512 4. a)73. 50 7. A TV costs £ 120, how much will it cost if its b) 77. 91 price is decreased by: c)91. 49 a) 19% 5. 6. b) 32% a)162 c) 79% b)220. 32 d) 73. 5% c)90 d) 322. 56 e) 42% e)368. 64 8. A car bought for £ 6, 500 depreciates in 7. value by 12. 5% each year, how much will it a)97. 20 b) 81. 60 be worth after: c)25. 20 a) 1 year d)31. 80 b) 2 years e)69. 60 8. c) 5 years? a)5687. 50 b) 4976. 56 c)333. 91 Percentage Increase/Decrease 1. Explain how you would use a calculator to increase an amount by a given percent. 2. Increase the following amounts by 42% a)£ 225 b) £ 306 c)£ 125 d)£ 448 e)£ 512 3. A TV costs £ 120, how much will it cost if its price is increased by: a) 12% b)31% c)55% d)62. 5% e)99. 9% 4. Simon puts £ 70 in a bank, each year the money in his bank increase by 5. 5%, how much does he have in: a) 1 year b)2 years c)5 years? Home

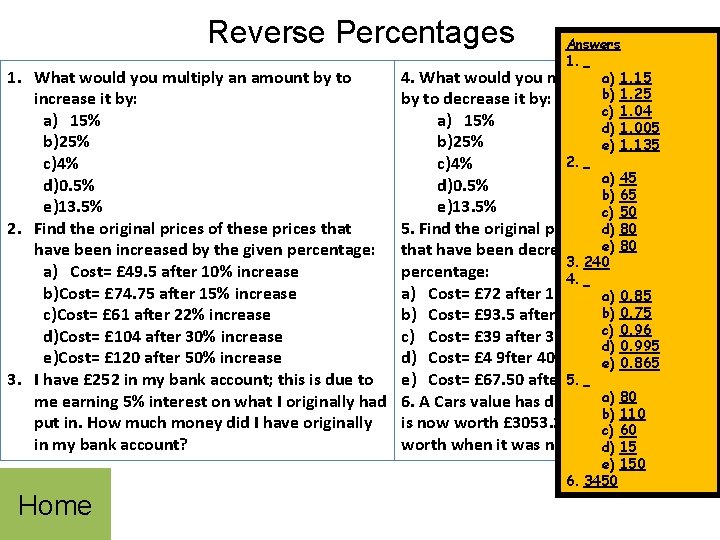
Reverse Percentages 1. What would you multiply an amount by to increase it by: a) 15% b)25% c)4% d)0. 5% e)13. 5% 2. Find the original prices of these prices that have been increased by the given percentage: a) Cost= £ 49. 5 after 10% increase b)Cost= £ 74. 75 after 15% increase c)Cost= £ 61 after 22% increase d)Cost= £ 104 after 30% increase e)Cost= £ 120 after 50% increase 3. I have £ 252 in my bank account; this is due to me earning 5% interest on what I originally had put in. How much money did I have originally in my bank account? Home Answers 1. 4. What would you multiply an amount a) 1. 15 b) 1. 25 by to decrease it by: c) 1. 04 a) 15% d) 1. 005 b)25% e) 1. 135 2. c)4% a) 45 d)0. 5% b) 65 e)13. 5% c) 50 5. Find the original prices of these items d) 80 e) 80 that have been decreased by the given 3. 240 percentage: 4. a) Cost= £ 72 after 10% decrease a) 0. 85 b) 0. 75 b) Cost= £ 93. 5 after 15% decrease c) 0. 96 c) Cost= £ 39 after 35% decrease d) 0. 995 d) Cost= £ 4 9 fter 40% decrease e) 0. 865 e) Cost= £ 67. 50 after 55% decrease 5. a) 80 6. A Cars value has dropped by 11. 5% it b) 110 is now worth £ 3053. 25, what was it c) 60 worth when it was new? d) 15 e) 150 6. 3450