Independent Component Analysis ICA Adopted from Independent Component

Independent Component Analysis (ICA) Adopted from: Independent Component Analysis: A Tutorial Aapo Hyvärinen and Erkki Oja Helsinki University of Technology

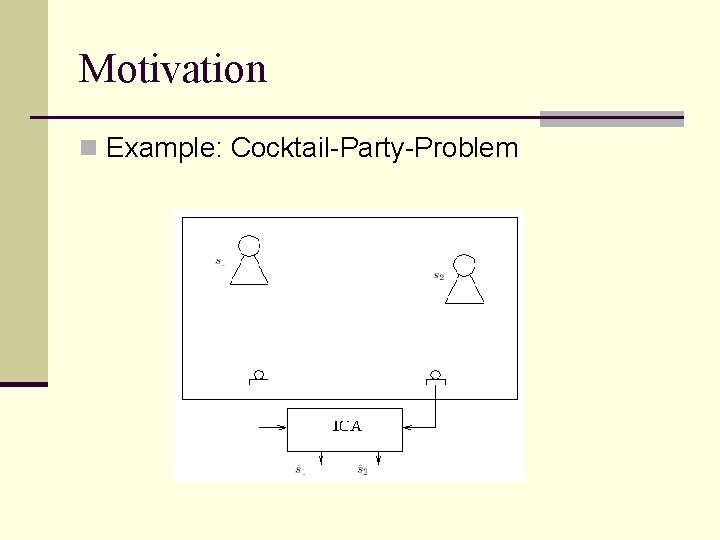
Motivation n Example: Cocktail-Party-Problem

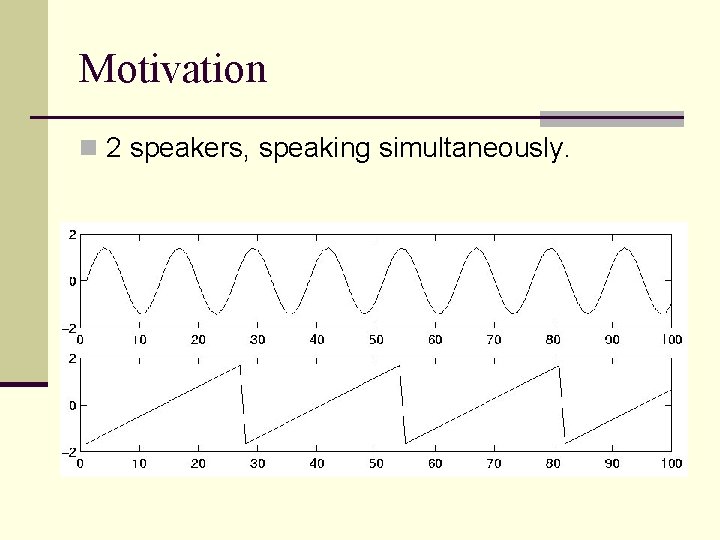
Motivation n 2 speakers, speaking simultaneously.

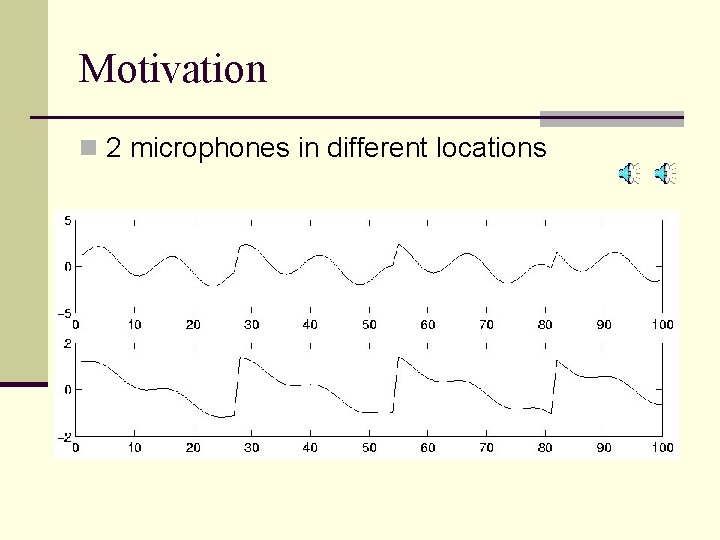
Motivation n 2 microphones in different locations

Motivation aij. . . depends on the distances of the microphones from the speakers

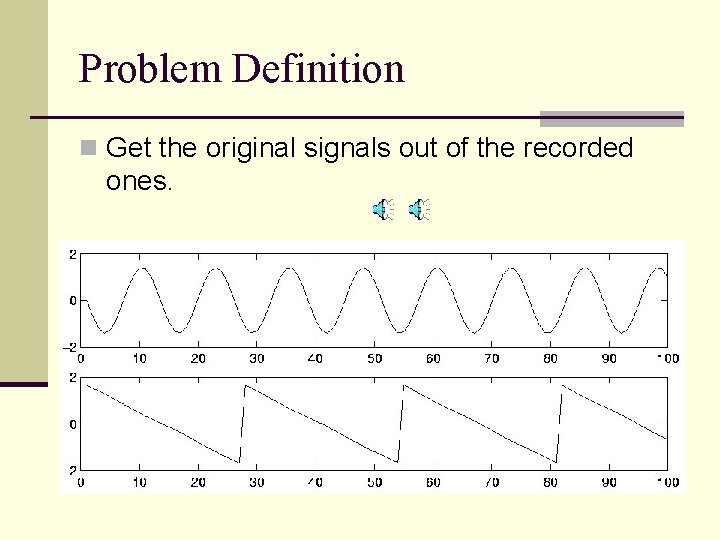
Problem Definition n Get the original signals out of the recorded ones.

Noise-free ICA model n Use statistical „latent variables“ system n Random variable sk instead of time signal n xj = aj 1 s 1 + aj 2 s 2 +. . + ajnsn, for all j x = As x = Sum(aisi) n ai. . . basis functions n si. . . independent components (IC‘s)

Generative Model n IC‘s s are latent variables => unknown n Mixing matrix A is also unknown n Task: estimate A and s using only the observeable random vector x

Restrictions n si are statistically independent n p(y 1, y 2) = p(y 1)p(y 2) n Non-gaussian distributions n Note: if only one IC is gaussian, the estimation is still possible

Solving the ICA model n Additional assumptions: n # of IC‘s = # of observable mixtures n => A is square and invertible n A is identifiable => estimate A n Compute W = A-1 n Obtain IC‘s from: s = Wx

Ambiguities (I) n Can‘t determine the variances (energies) of the IC‘s x = Sum[(1/Ci)aisi. Ci] n Fix magnitudes of IC‘s assuming unit variance: E{si 2} = 1 n Only ambiguity of sign remains n

Ambiguities (II) n Can‘t determine the order of the IC‘s n Terms can be freely interchanged, because both s and A are unknown n x = AP-1 Ps n P. . . permutation matrix

Centering the variables n Simplifying the algorithm: n Assume that both x and s have zero mean n Preprocessing: x = x‘ – E{x‘} n IC‘s are also zero mean because of: E{s} = A-1 E{x} n After ICA: add A-1 E{x‘} to zero mean IC‘s

Noisy ICA model x = As + n n A. . . mxn mixing matrix n s. . . n-dimensional vector of IC‘s n n. . . m-dimensional random noise vector n Same assumptions as for noise-free model

General ICA model n Find a linear transformation: n n s = Wx si as independent as possible Maximize F(s) : Measure of independence No assumptions on data Problem: n n definition for measure of independence Strict independence is in general impossible

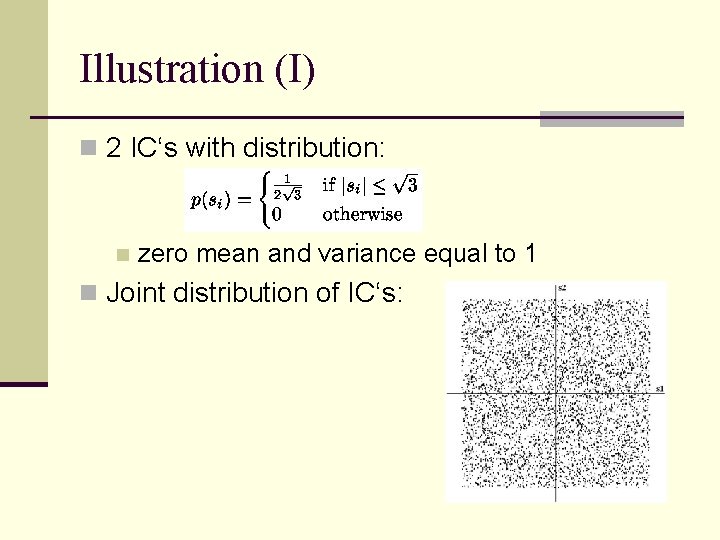
Illustration (I) n 2 IC‘s with distribution: n zero mean and variance equal to 1 n Joint distribution of IC‘s:

Illustration (II) n Mixing matrix: n Joint distribution of observed mixtures:

Other Problems n Blind Source/Signal Separation (BSS) n Cocktail Party Problem (another definition) n Electroencephalogram n Radar n Mobile Communication n Feature extraction n Image, Audio, Video, . . . representation

Principles of ICA Estimation n “Nongaussian is independent”: central limit theorem n Measure of nonguassianity n Kurtosis: (Kurtosis=0 for a gaussian distribution) n Negentropy: a gaussian variable has the largest entropy among all random variables of equal variance:

Approximations of Negentropy (1)

Approximations of Negentropy (2)

The Fast. ICA Algorithm

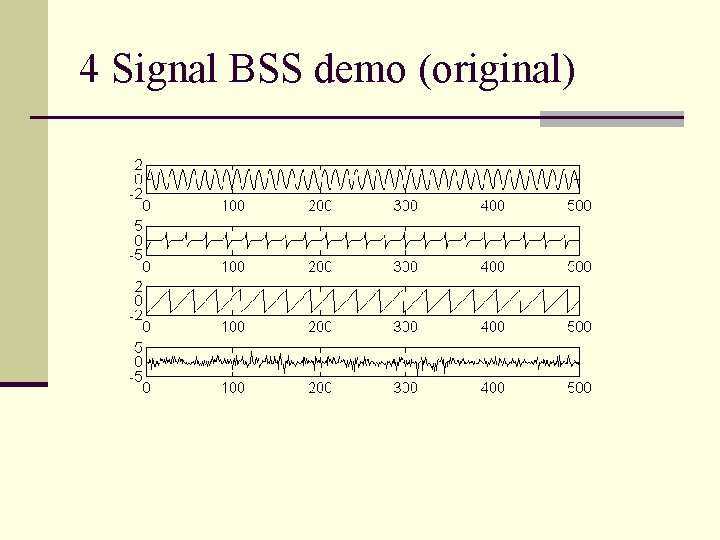
4 Signal BSS demo (original)

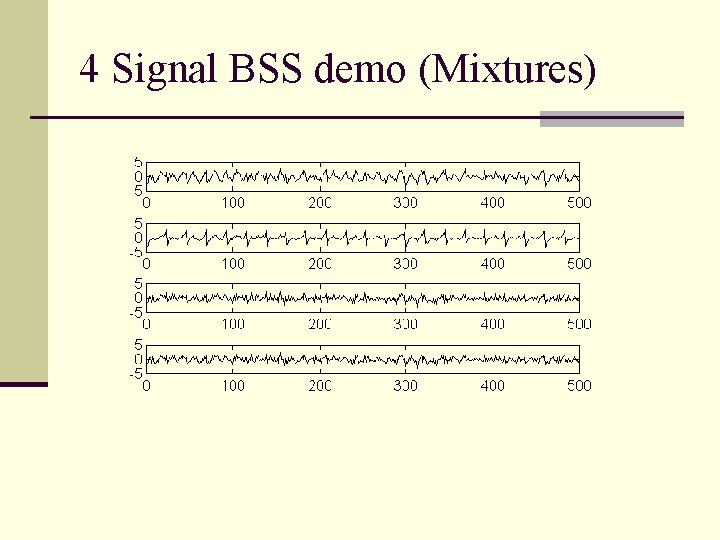
4 Signal BSS demo (Mixtures)

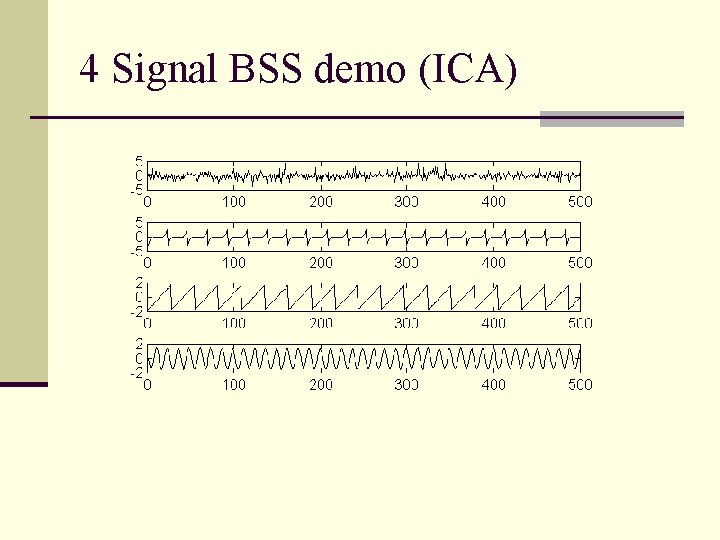
4 Signal BSS demo (ICA)

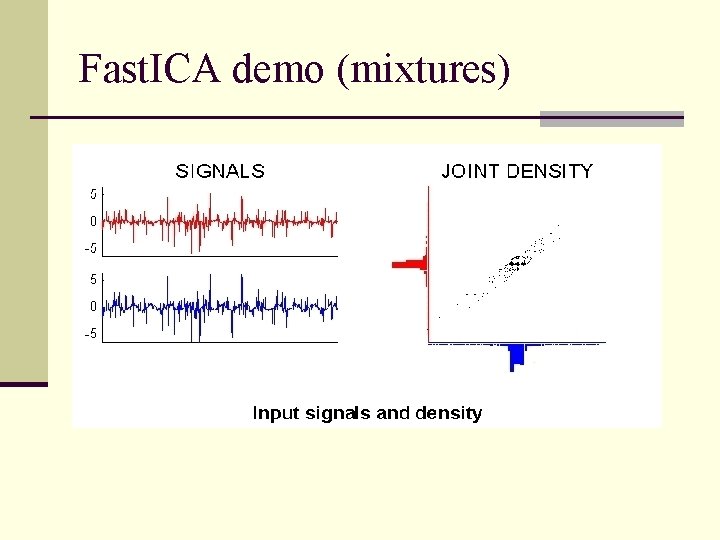
Fast. ICA demo (mixtures)

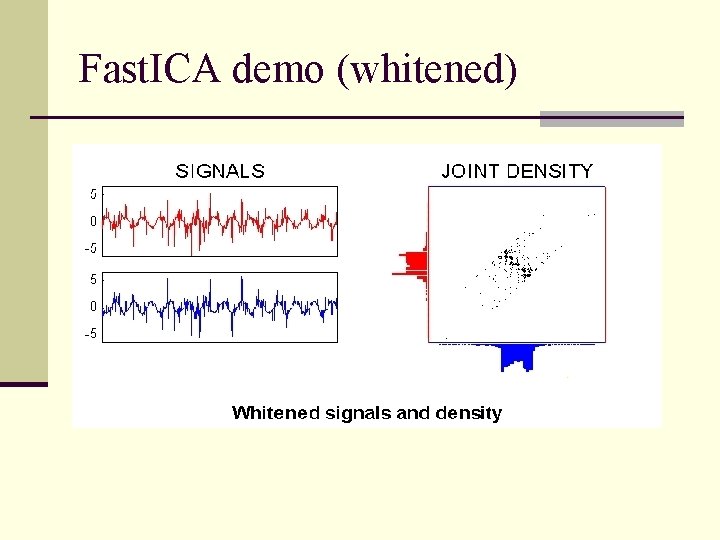
Fast. ICA demo (whitened)

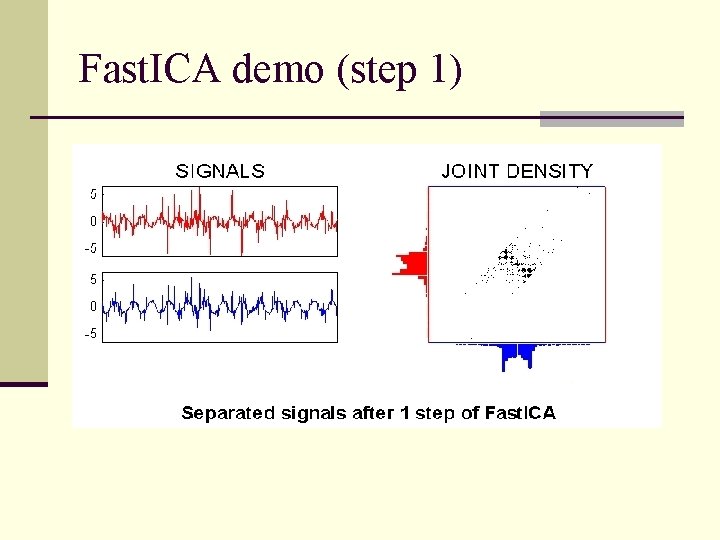
Fast. ICA demo (step 1)

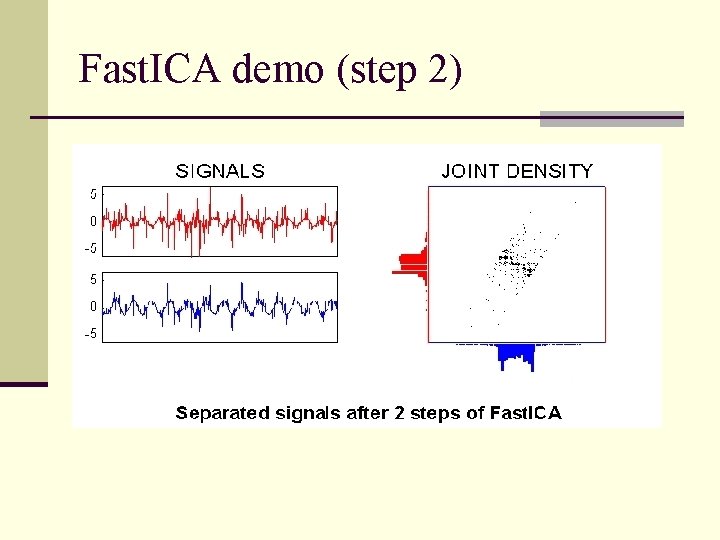
Fast. ICA demo (step 2)

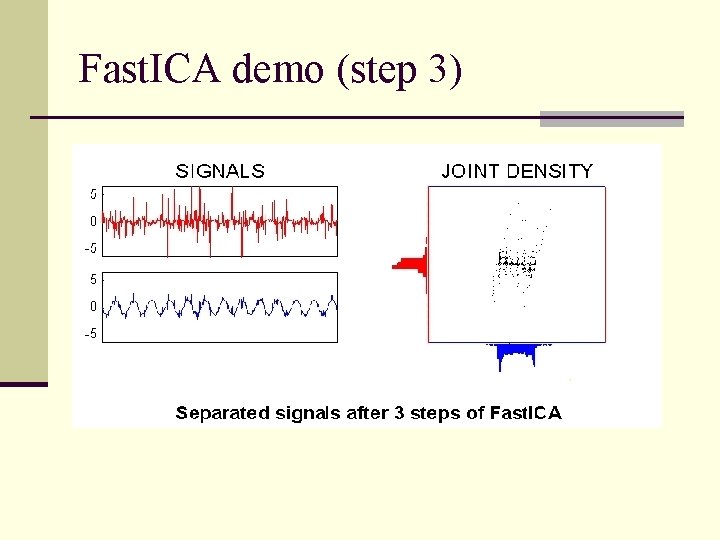
Fast. ICA demo (step 3)

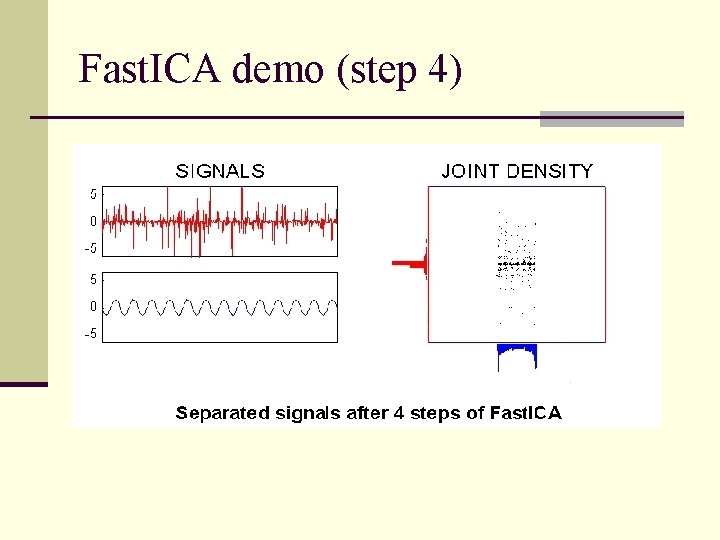
Fast. ICA demo (step 4)

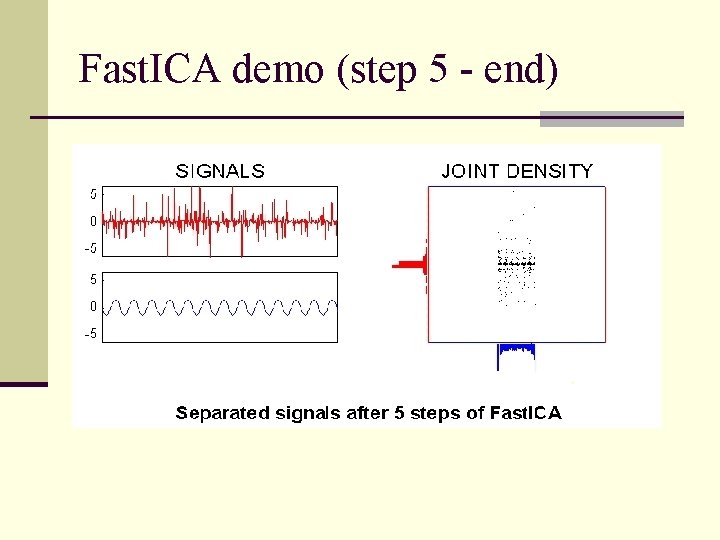
Fast. ICA demo (step 5 - end)

Other Algorithms for BSS n Temporal Predictability n TP of mixture < TP of any source signal n Maximize TP to seperate signals n Works also on signals with Gaussian PDF n Co. Bli. SS n Works in frequency domain n Only using the covariance matrix of the observation n JADE

Links 1 n Feature extraction (Images, Video) n http: //hlab. phys. rug. nl/demos/ica/ n Aapo Hyvarinen: ICA (1999) n http: //www. cis. hut. fi/aapo/papers/NCS 99 web/node 11. ht ml n ICA demo step-by-step n http: //www. cis. hut. fi/projects/icademo/ n Lots of links n http: //sound. media. mit. edu/~paris/ica. html

Links 2 n object-based audio capture demos n http: //www. media. mit. edu/~westner/sepdemo. html n Demo for BBS with „Co. Bli. SS“ (wav-files) n http: //www. esp. ele. tue. nl/onderzoek/daniels/BSS. html n Tomas Zeman‘s page on BSS research n http: //ica. fun-thom. misto. cz/page 3. html n Virtual Laboratories in Probability and Statistics n http: //www. math. uah. edu/stat/index. html

Links 3 n An efficient batch algorithm: JADE n http: //www-sig. enst. fr/~cardoso/guidesepsou. html n Dr JV Stone: ICA and Temporal Predictability n http: //www. shef. ac. uk/~pc 1 jvs/ n BBS with Degenerate Unmixing Estimation Technique (papers) n http: //www. princeton. edu/~srickard/bss. html

Links 4 n detailed information for scientists, engineers and industrials about ICA n http: //www. cnl. salk. edu/~tewon/ica_cnl. html n Fast. ICA package for matlab n http: //www. cis. hut. fi/projects/ica/fastica/fp. shtml n Aapo Hyvärinen n http: //www. cis. hut. fi/~aapo/ n Erkki Oja n http: //www. cis. hut. fi/~oja/