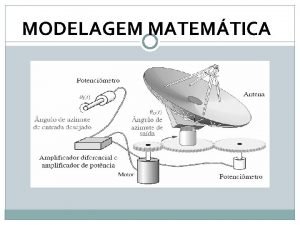
EE2402009 Modelamento EE2402009 Modelagem Caixa Transparente Caixa Opaca

EE-240/2009 Modelamento EE-240/2009

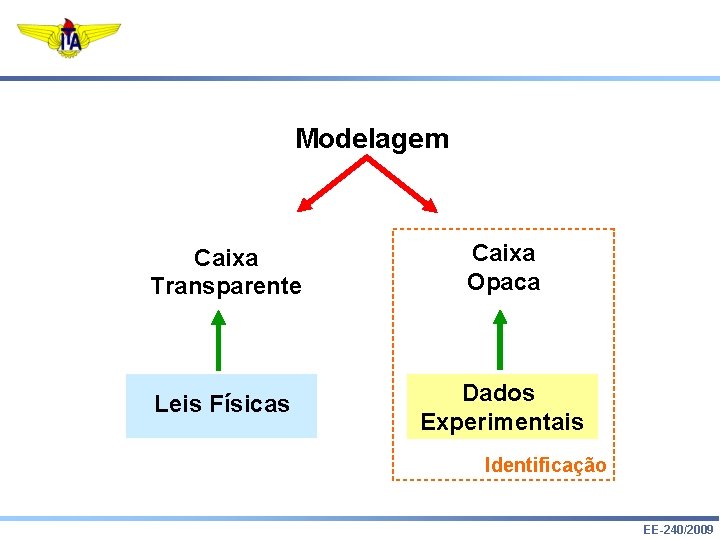
Modelagem Caixa Transparente Caixa Opaca Leis Físicas Dados Experimentais Identificação EE-240/2009

Caixa Transparente (Branca) EE-240/2009

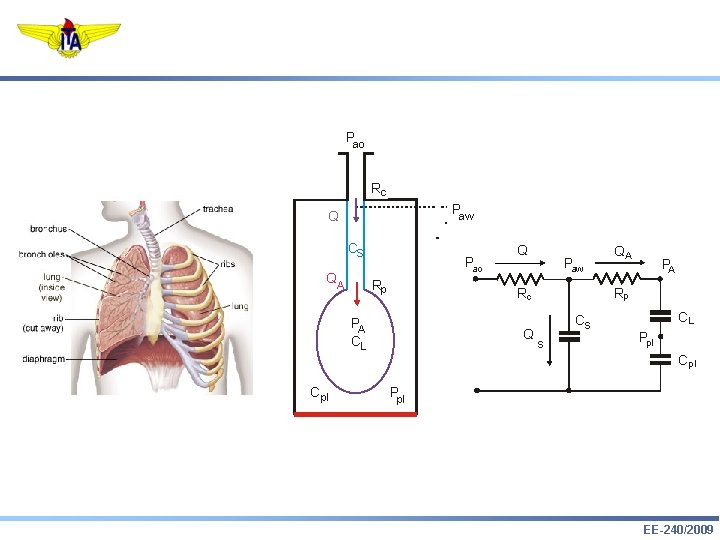
Pao Rc Paw Q CS QA Pao Rp Paw Q QA PA Rp Rc PA CL C pl Q CS S CL Ppl Cpl Ppl EE-240/2009

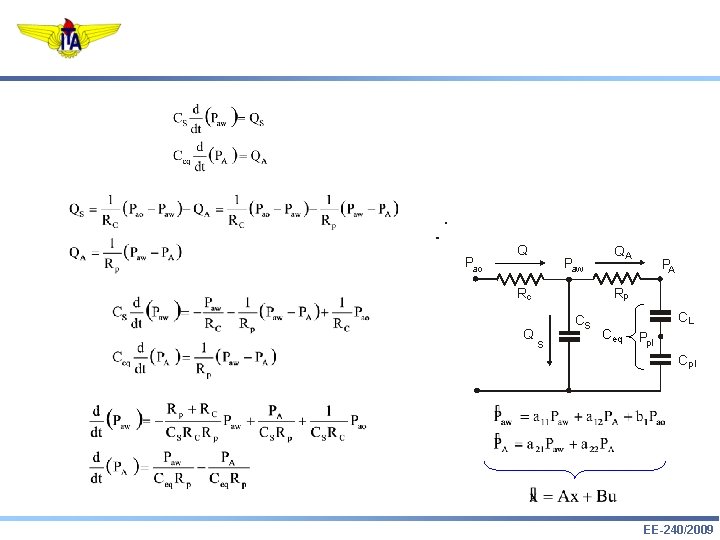
Pao Q Paw PA Rp Rc Q QA CS S Ceq CL Ppl Cpl EE-240/2009

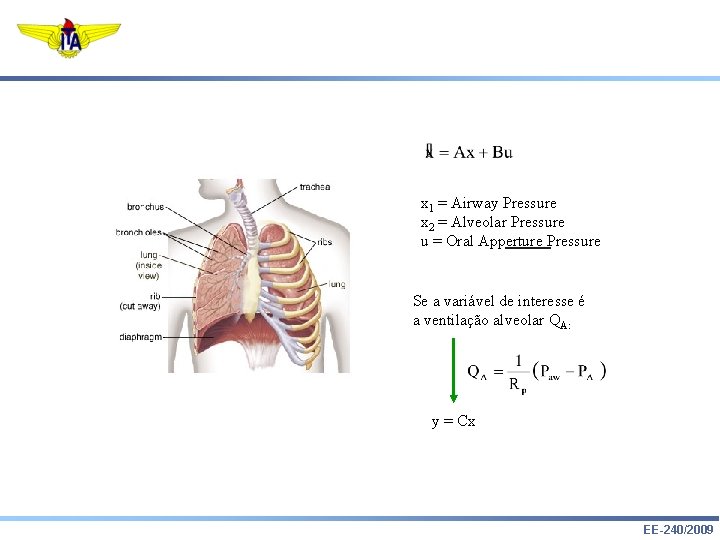
x 1 = Airway Pressure x 2 = Alveolar Pressure u = Oral Apperture Pressure Se a variável de interesse é a ventilação alveolar QA: y = Cx EE-240/2009

EE-240/2009

Caixa Opaca (Preta) EE-240/2009

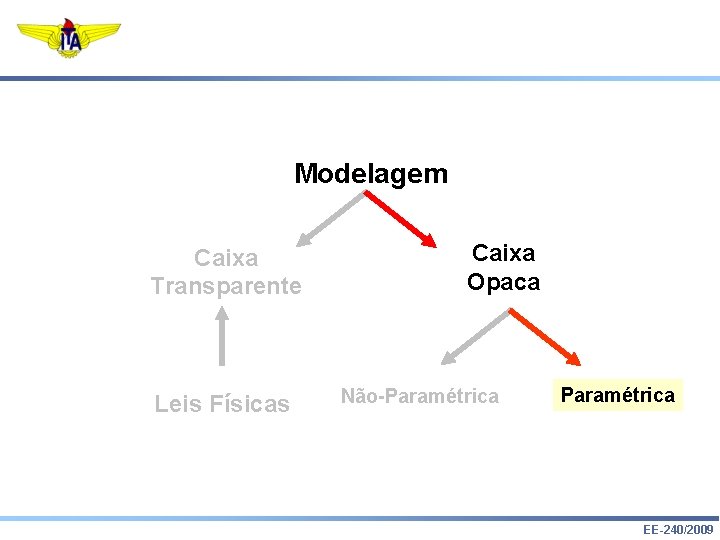
Modelagem Caixa Transparente Leis Físicas Caixa Opaca Não-Paramétrica EE-240/2009

Modelagem Caixa Transparente Leis Físicas Caixa Opaca Não-Paramétrica EE-240/2009

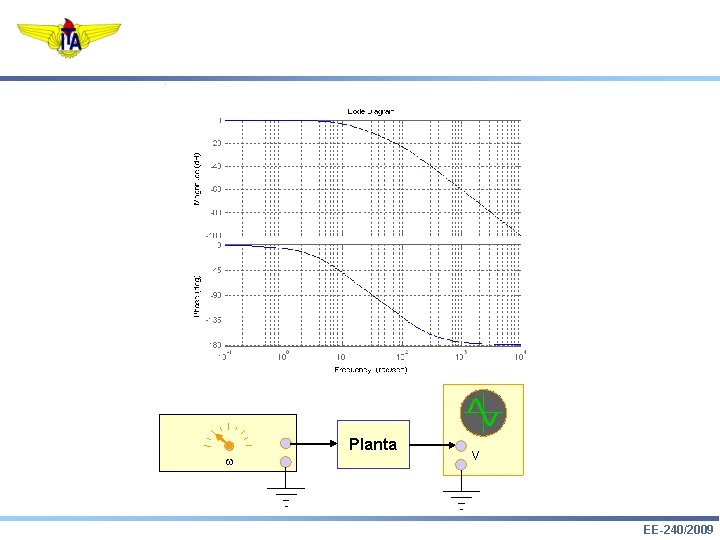
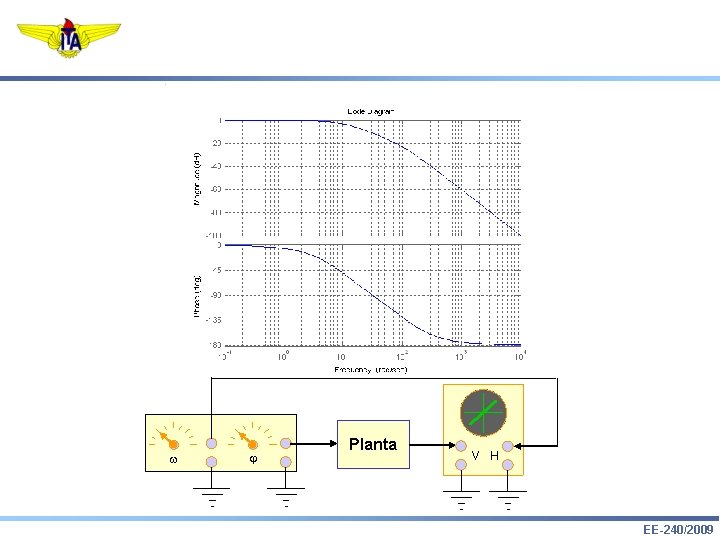
w Planta V EE-240/2009

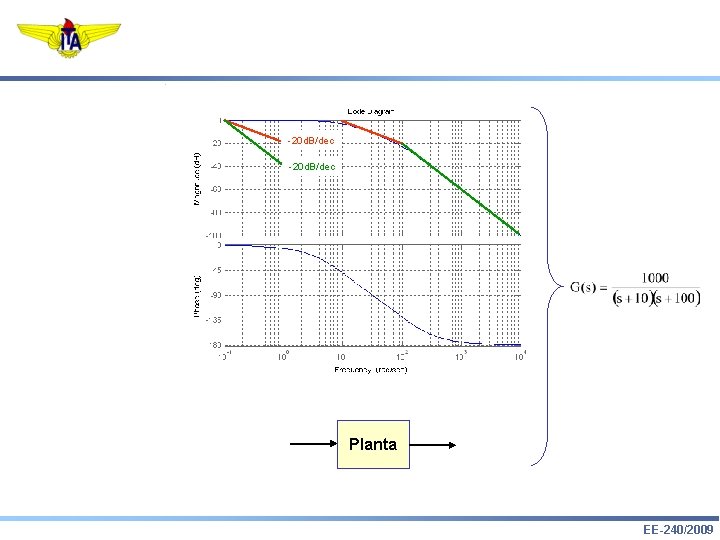
-20 d. B/dec Planta EE-240/2009

w j Planta V H EE-240/2009

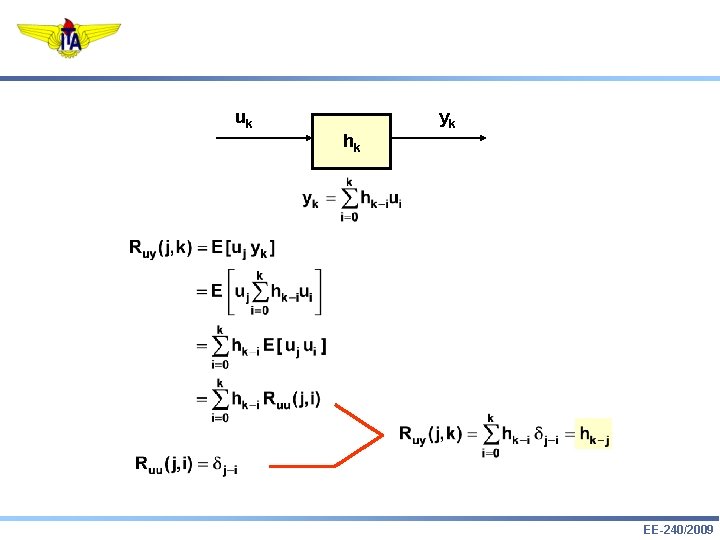
uk yk hk EE-240/2009

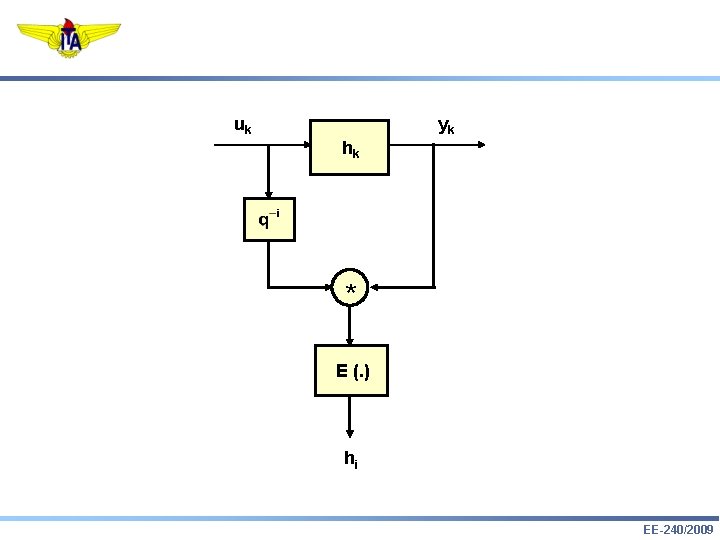
uk yk hk * E (. ) hi EE-240/2009

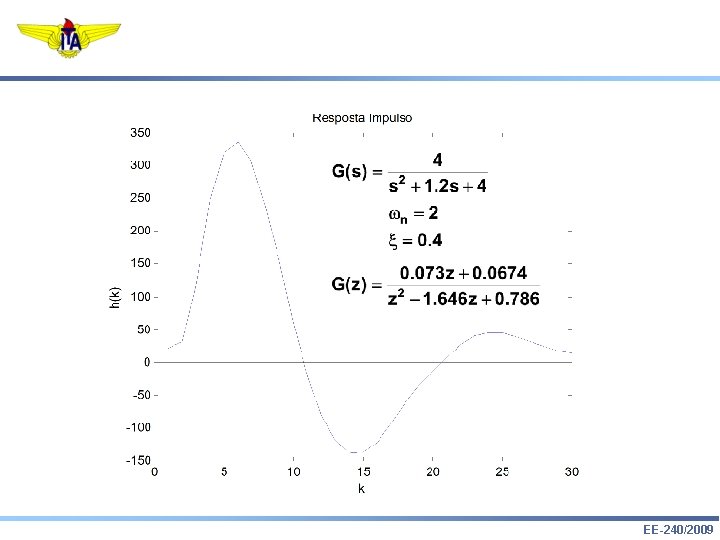
EE-240/2009

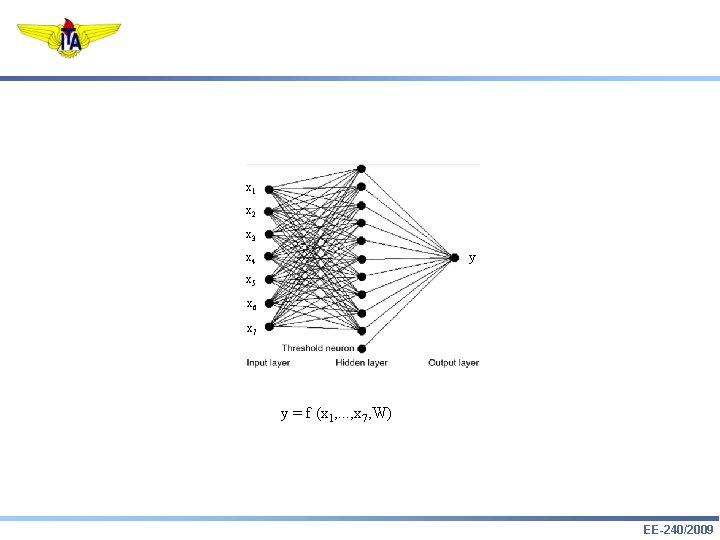
x 1 x 2 x 3 y x 4 x 5 x 6 x 7 y = f (x 1, . . . , x 7, W) EE-240/2009

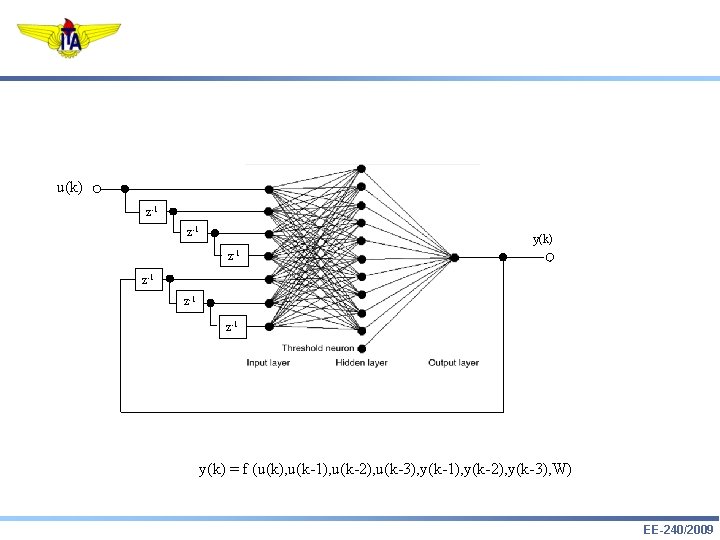
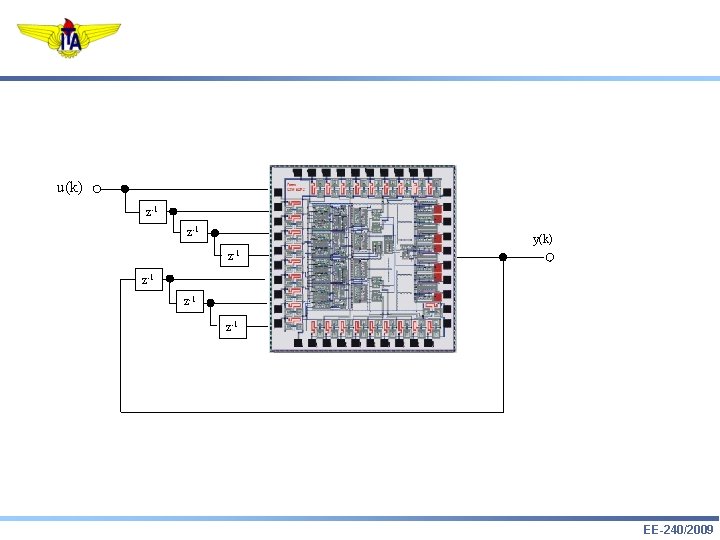
u(k) z-1 y(k) z-1 z-1 y(k) = f (u(k), u(k-1), u(k-2), u(k-3), y(k-1), y(k-2), y(k-3), W) EE-240/2009

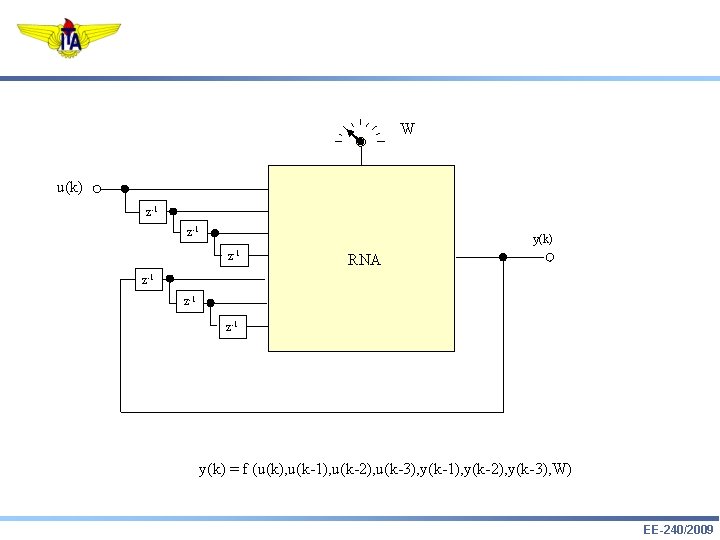
W u(k) z-1 y(k) z-1 RNA z-1 z-1 y(k) = f (u(k), u(k-1), u(k-2), u(k-3), y(k-1), y(k-2), y(k-3), W) EE-240/2009

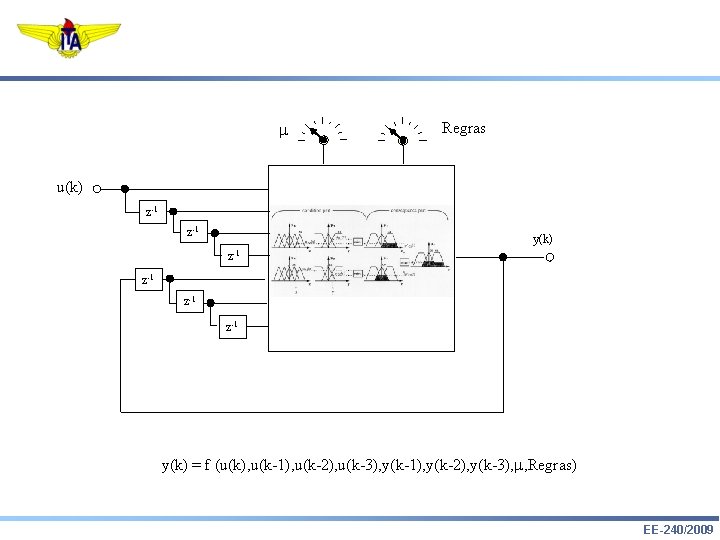
Regras u(k) z-1 y(k) z-1 z-1 y(k) = f (u(k), u(k-1), u(k-2), u(k-3), y(k-1), y(k-2), y(k-3), , Regras) EE-240/2009

u(k) z-1 y(k) z-1 z-1 EE-240/2009

Modelagem Caixa Transparente Leis Físicas Caixa Opaca Não-Paramétrica EE-240/2009

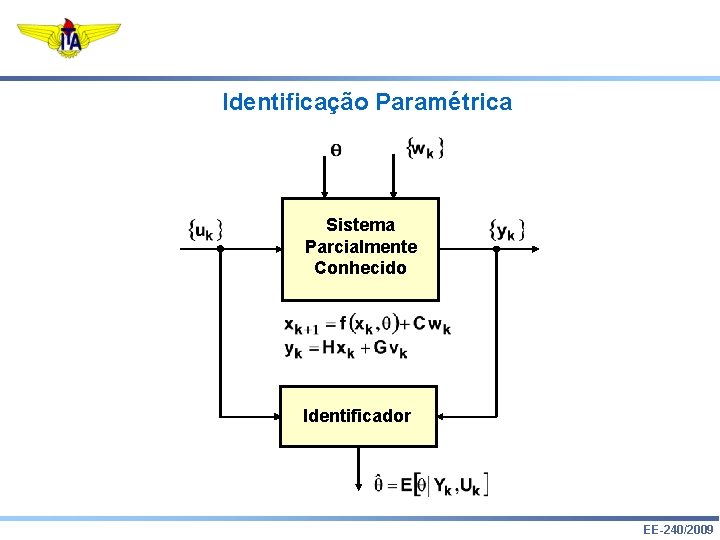
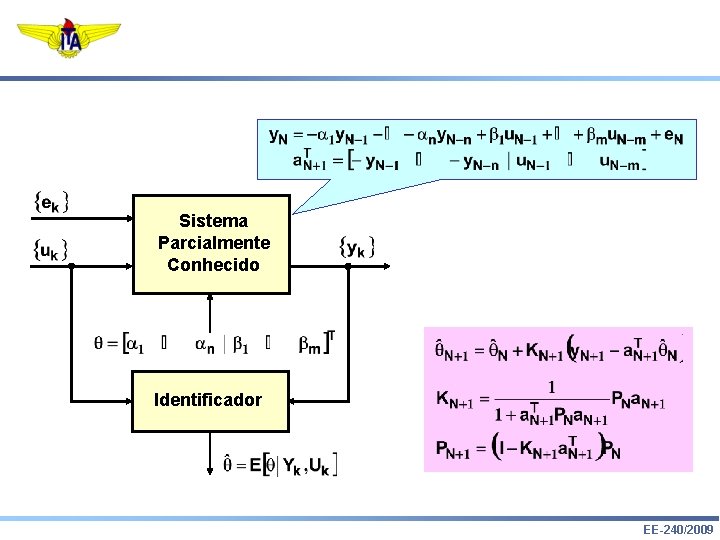
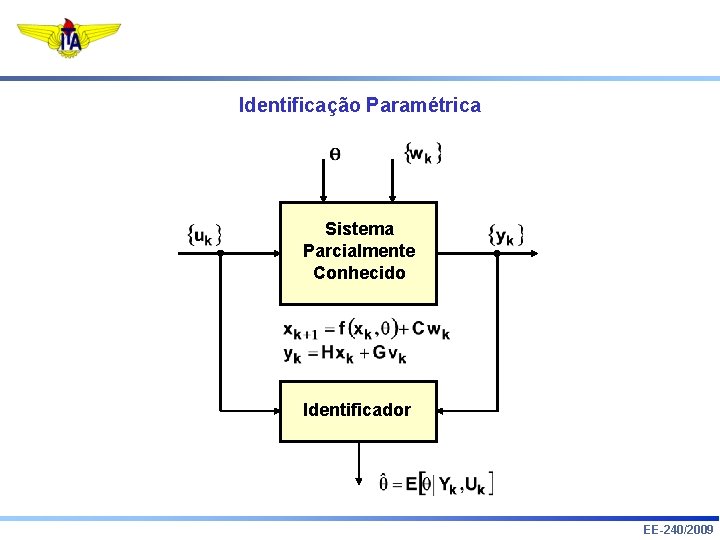
Identificação Paramétrica Sistema Parcialmente Conhecido Identificador EE-240/2009

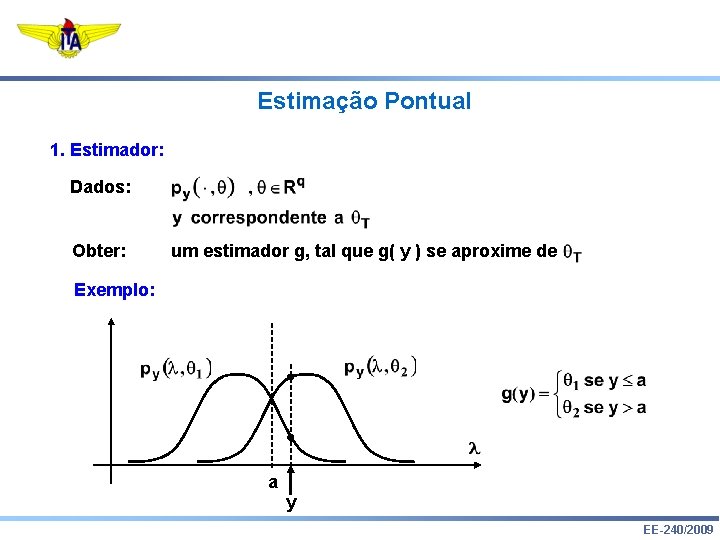
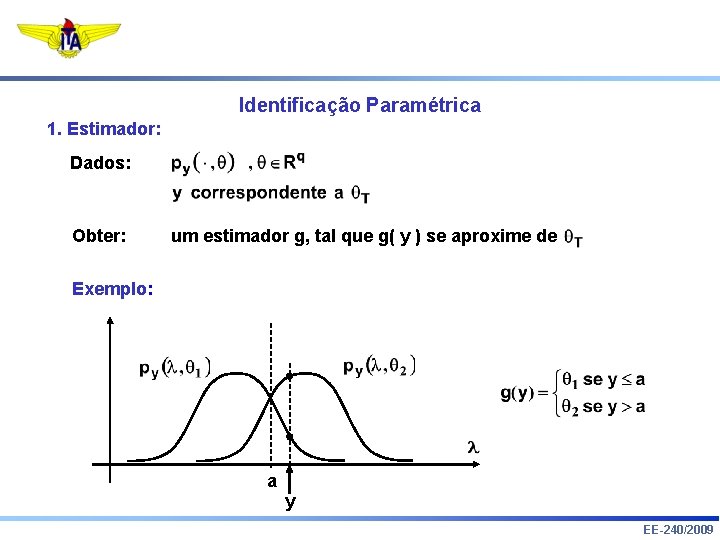
Estimação Pontual 1. Estimador: Dados: Obter: um estimador g, tal que g( y ) se aproxime de Exemplo: a y EE-240/2009

2. Estimador Não-Polarizado: Exemplo: Seja Obter LSE EE-240/2009

EE-240/2009

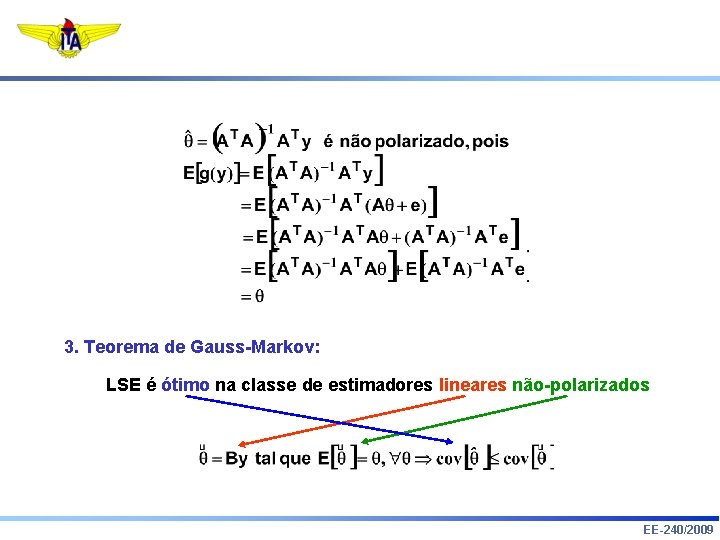
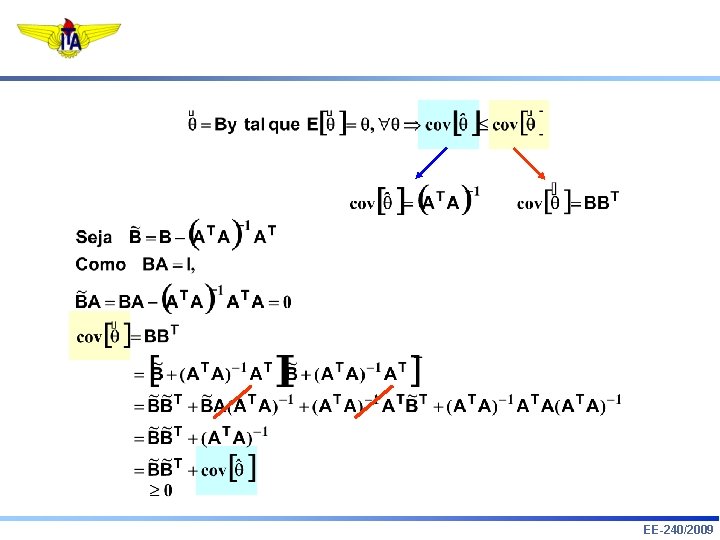
3. Teorema de Gauss-Markov: LSE é ótimo na classe de estimadores lineares não-polarizados EE-240/2009

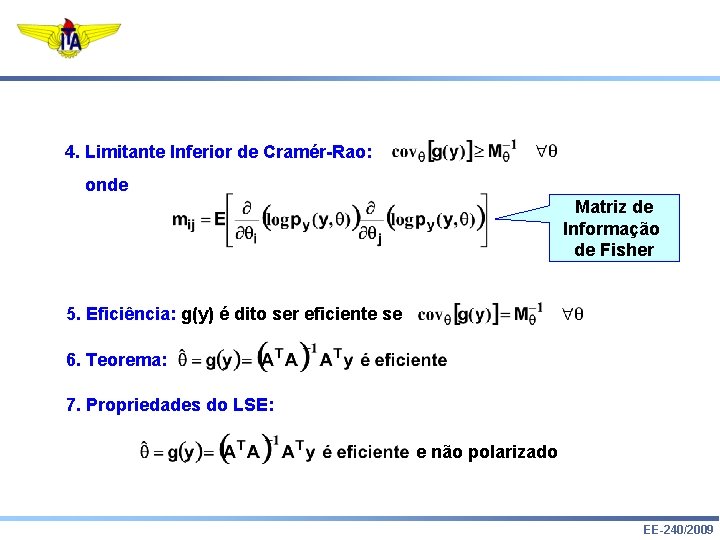
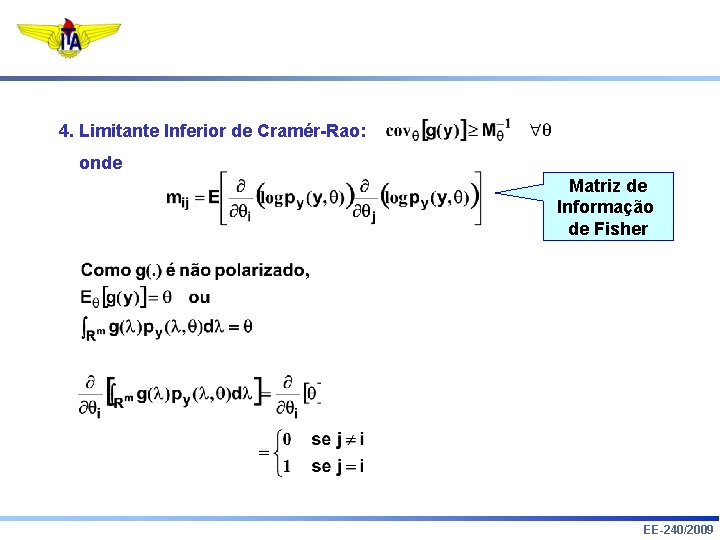
4. Limitante Inferior de Cramér-Rao: onde Matriz de Informação de Fisher 5. Eficiência: g(y) é dito ser eficiente se 6. Teorema: 7. Propriedades do LSE: e não polarizado EE-240/2009

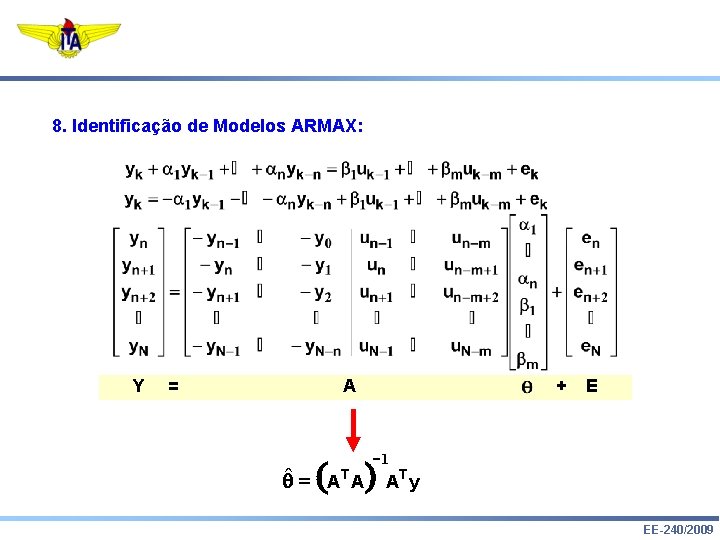
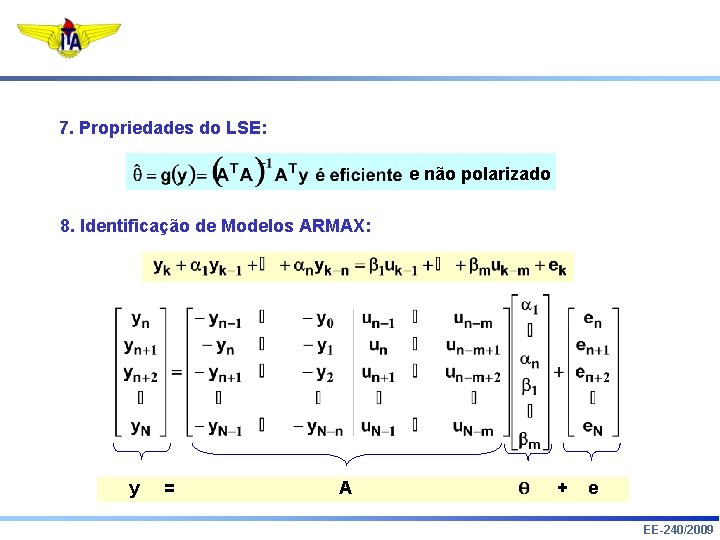
8. Identificação de Modelos ARMAX: Y = A ( qˆ = A T A + E -1 ) AT y EE-240/2009

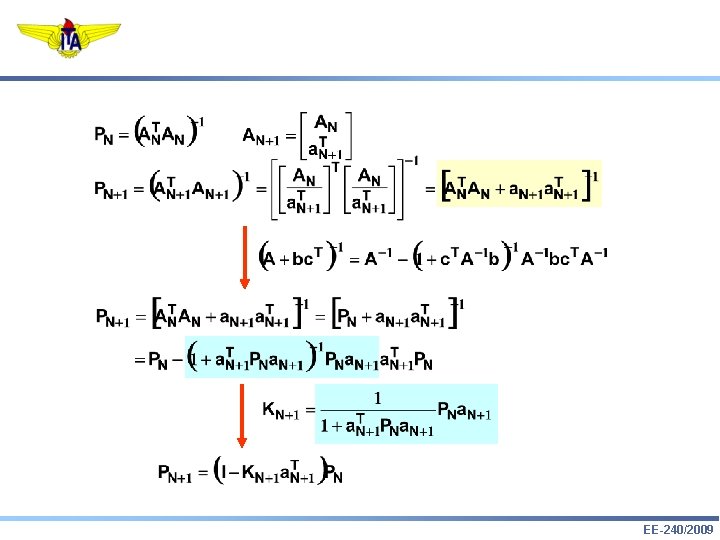
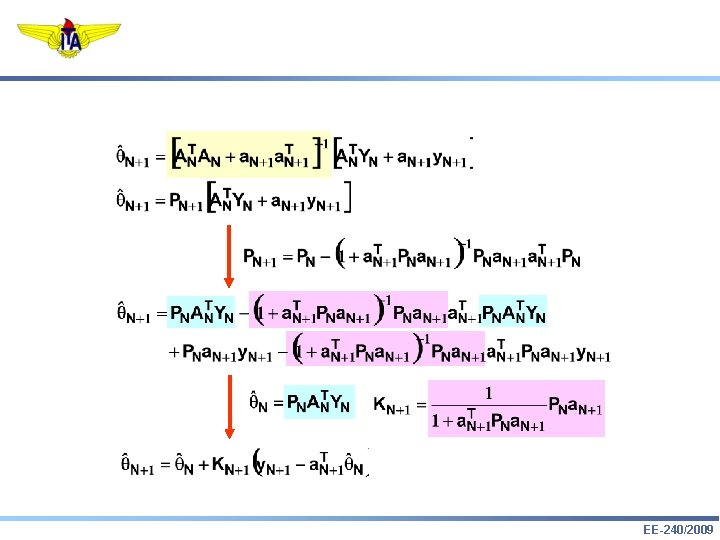
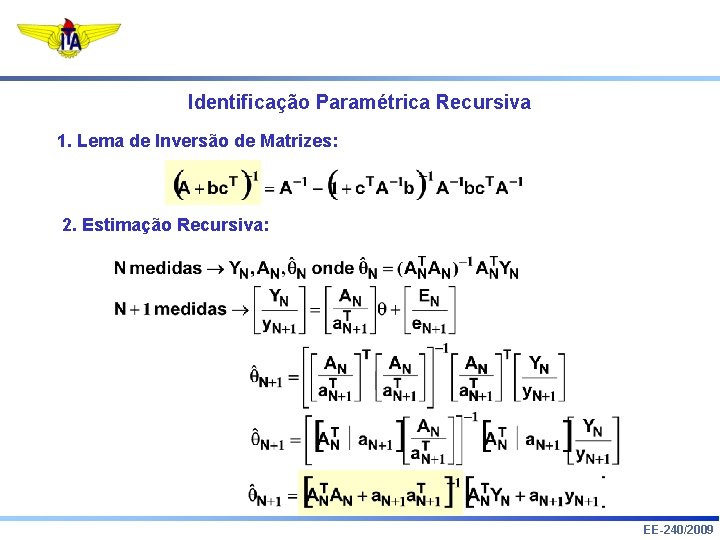
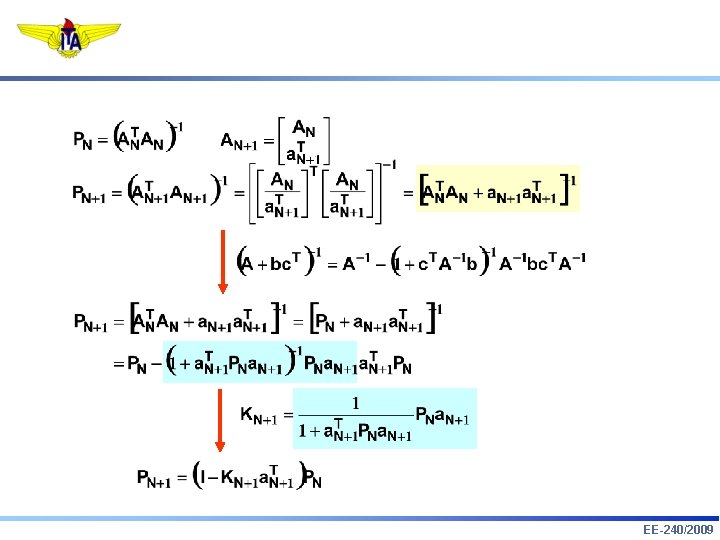
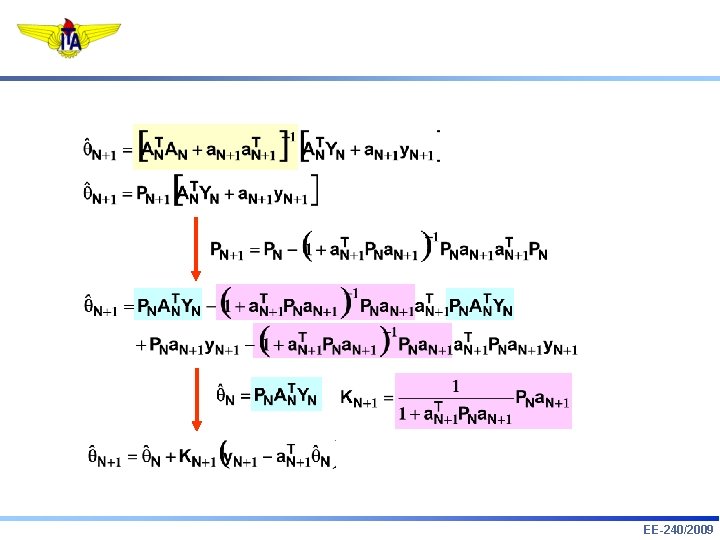
9. Lema de Inversão de Matrizes: 10. Estimação Recursiva: EE-240/2009

EE-240/2009

EE-240/2009

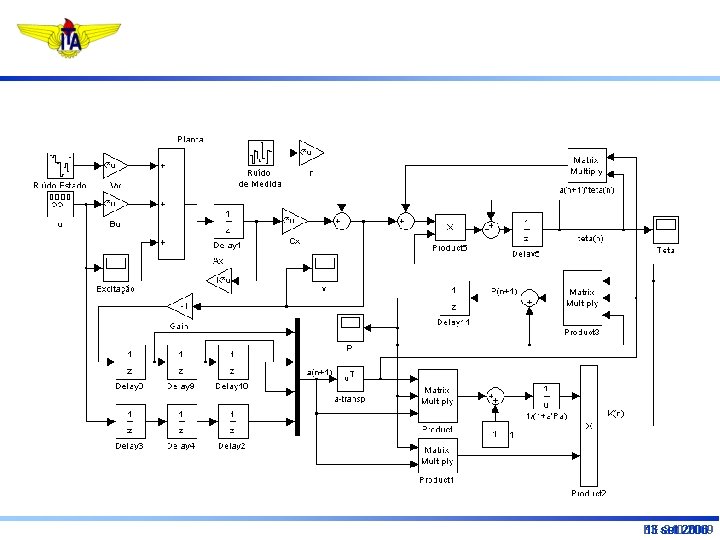
Sistema Parcialmente Conhecido Identificador EE-240/2009

Exemplo: EE-240/2009 13 set 2006

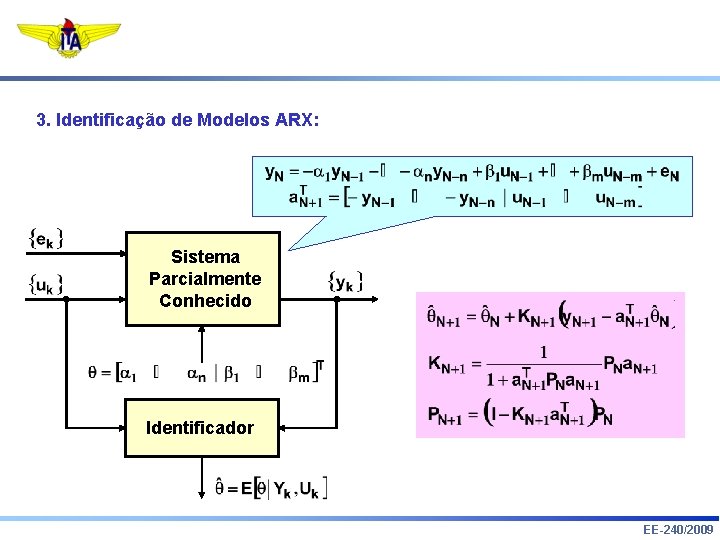
Identificação Paramétrica Sistema Parcialmente Conhecido Identificador EE-240/2009

Identificação Paramétrica 1. Estimador: Dados: Obter: um estimador g, tal que g( y ) se aproxime de Exemplo: a y EE-240/2009

2. Estimador Não - Polarizado: Exemplo: Seja Obter LSE EE-240/2009

3. Teorema de Gauss-Markov: LSE é ótimo na classe de estimadores lineares não-polarizados EE-240/2009

EE-240/2009

EE-240/2009

EE-240/2009

4. Limitante Inferior de Cramér-Rao: onde Matriz de Informação de Fisher EE-240/2009

Por outro lado, EE-240/2009

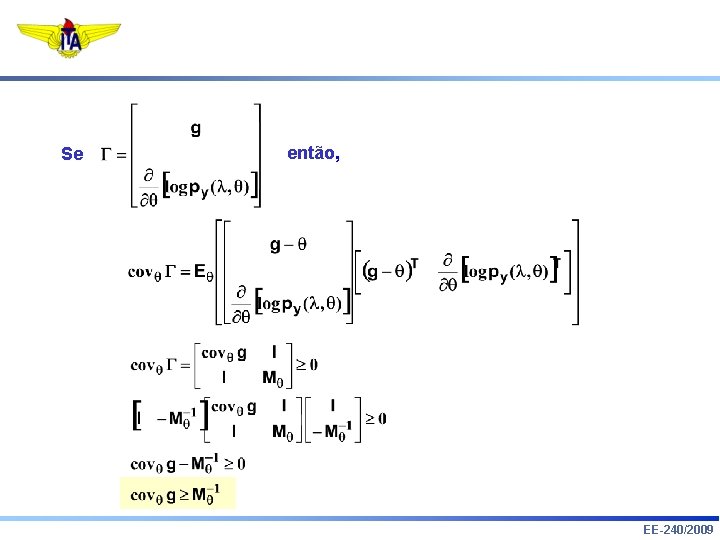
Se então, EE-240/2009

5. Eficiência: g(y) é dito ser eficiente se 6. Teorema: EE-240/2009

7. Propriedades do LSE: e não polarizado 8. Identificação de Modelos ARMAX: y = A + e EE-240/2009

Identificação Paramétrica Recursiva 1. Lema de Inversão de Matrizes: 2. Estimação Recursiva: EE-240/2009

EE-240/2009

EE-240/2009

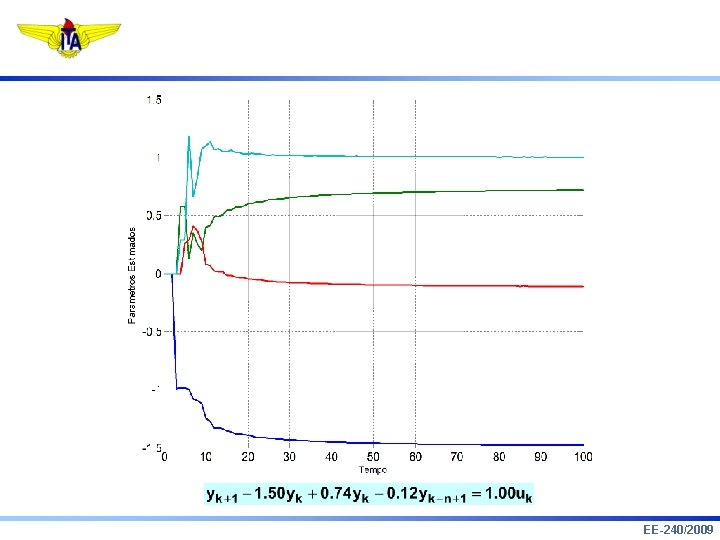
3. Identificação de Modelos ARX: Sistema Parcialmente Conhecido Identificador EE-240/2009

Exemplo: EE-240/2009

EE-240/2009 13 set 2006

EE-240/2009

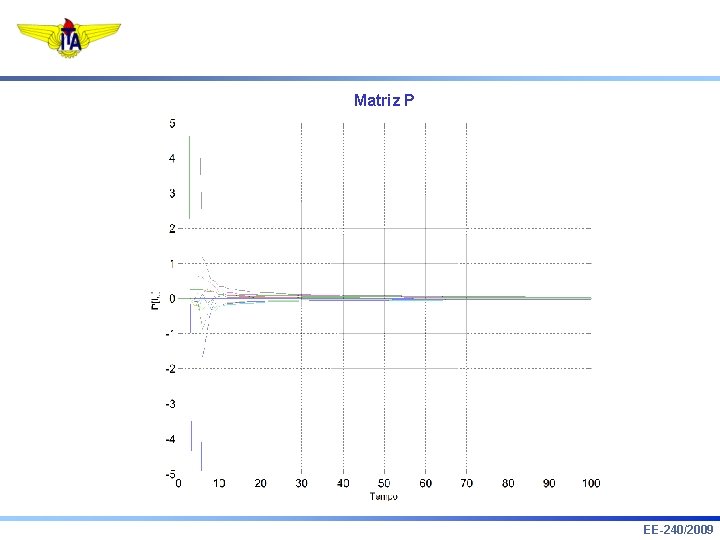
Matriz P EE-240/2009

4. Região de Confiança quando e ~ N(0 , 2 I ) e é conhecido: EE-240/2009

5. Região de Confiança quando e ~ N(0 , 2 I ) e é desconhecido: EE-240/2009

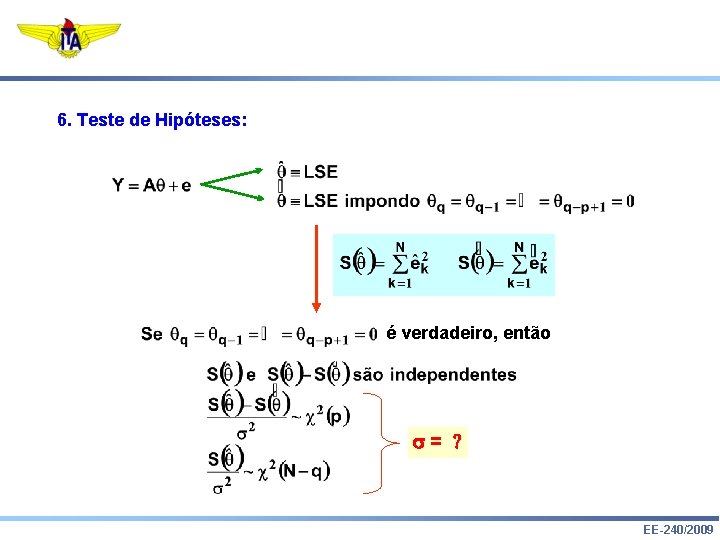
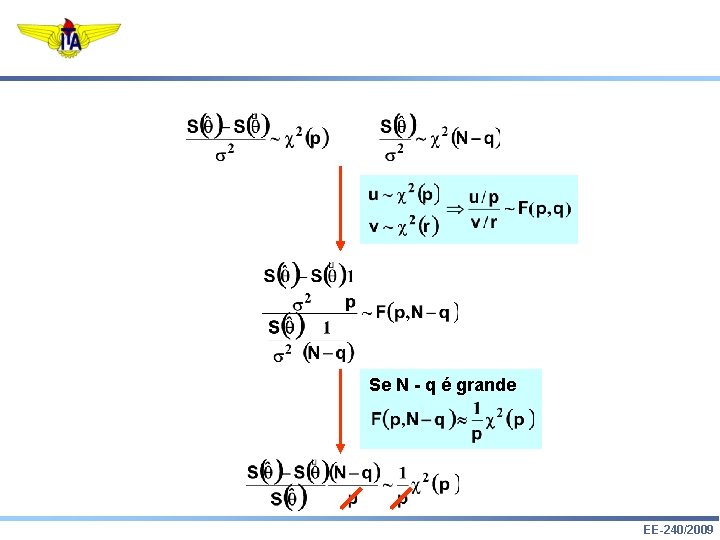
6. Teste de Hipóteses: é verdadeiro, então = EE-240/2009

Se N - q é grande EE-240/2009

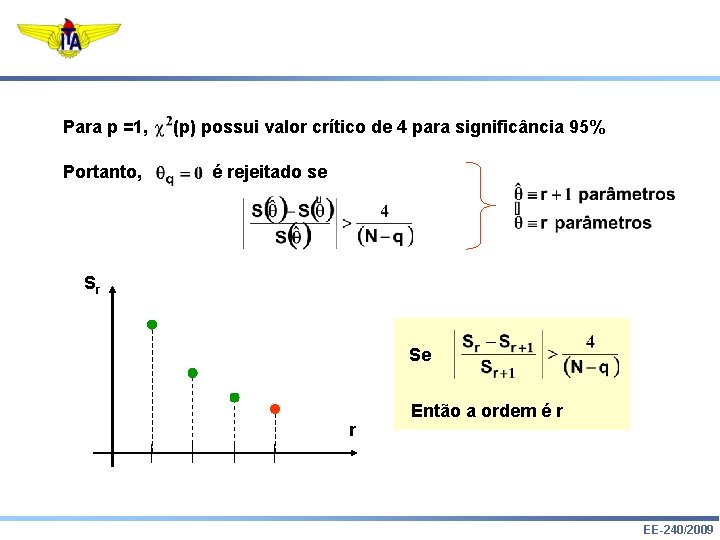
Para p =1, Portanto, (p) possui valor crítico de 4 para significância 95% é rejeitado se Sr Se r Então a ordem é r EE-240/2009

Muito Obrigado! EE-240/2009