CURSO DE MATEMTICA S DISCRETAS PARTE 1 LOGICA















- Slides: 68

CURSO DE MATEMÁTICA S DISCRETAS

PARTE 1 LOGICA

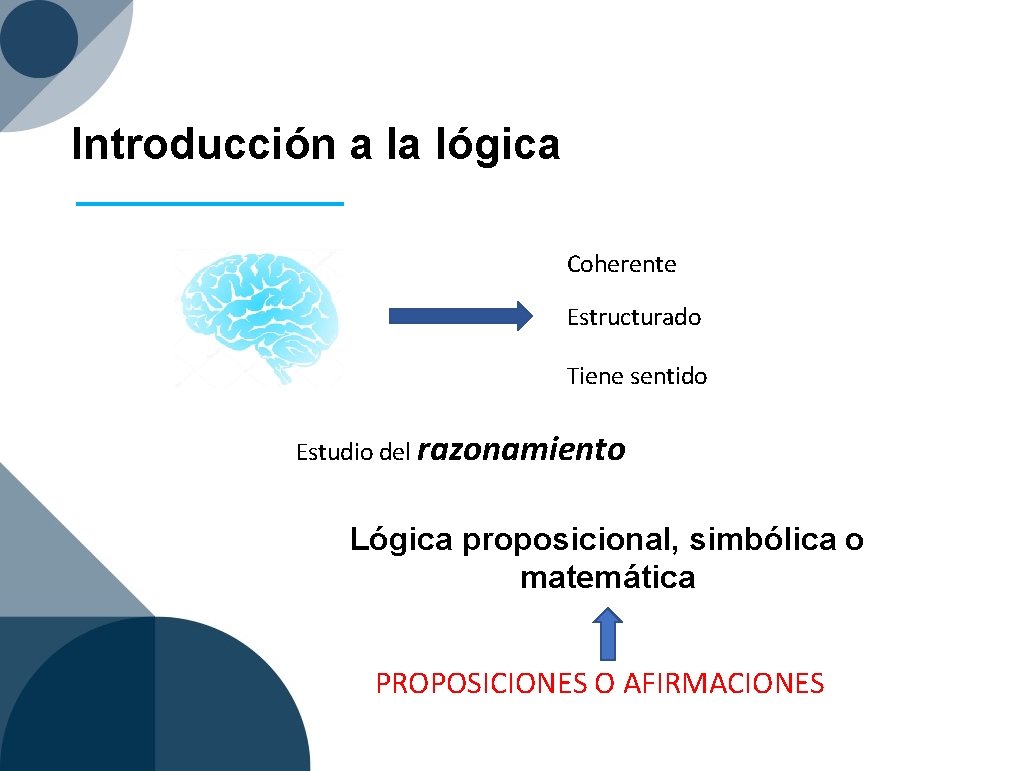
Introducción a la lógica Coherente Estructurado Tiene sentido Estudio del razonamiento Lógica proposicional, simbólica o matemática PROPOSICIONES O AFIRMACIONES

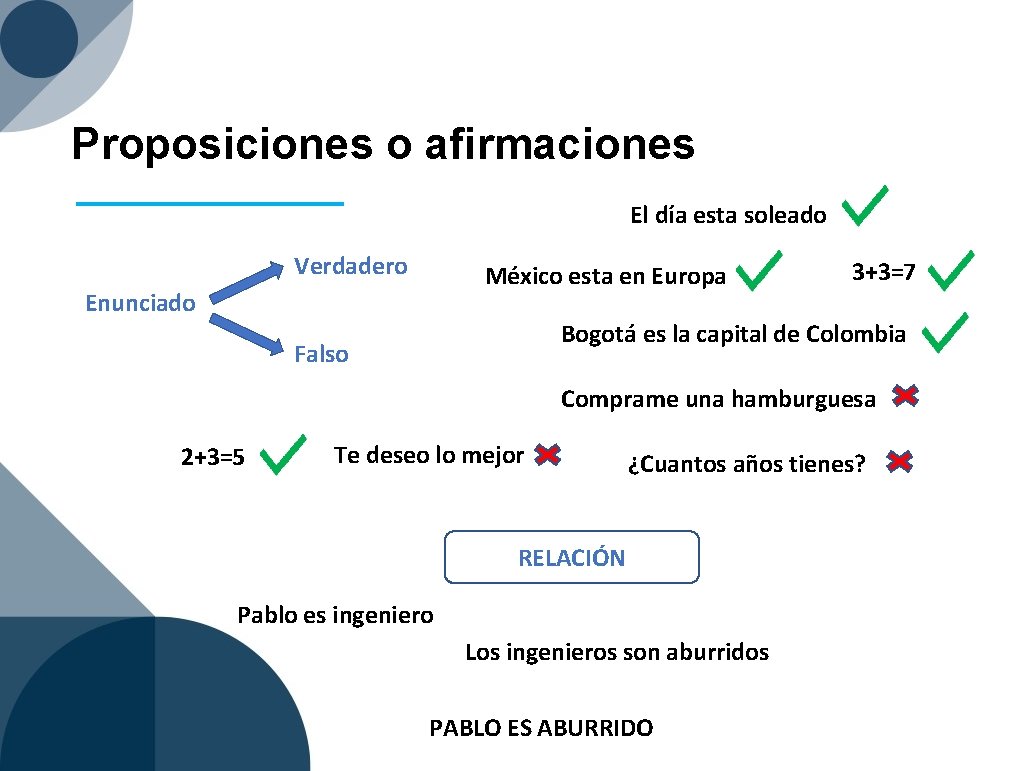
Proposiciones o afirmaciones El día esta soleado Verdadero México esta en Europa Enunciado 3+3=7 Bogotá es la capital de Colombia Falso Comprame una hamburguesa 2+3=5 Te deseo lo mejor ¿Cuantos años tienes? RELACIÓN Pablo es ingeniero Los ingenieros son aburridos PABLO ES ABURRIDO

Proposiciones simples

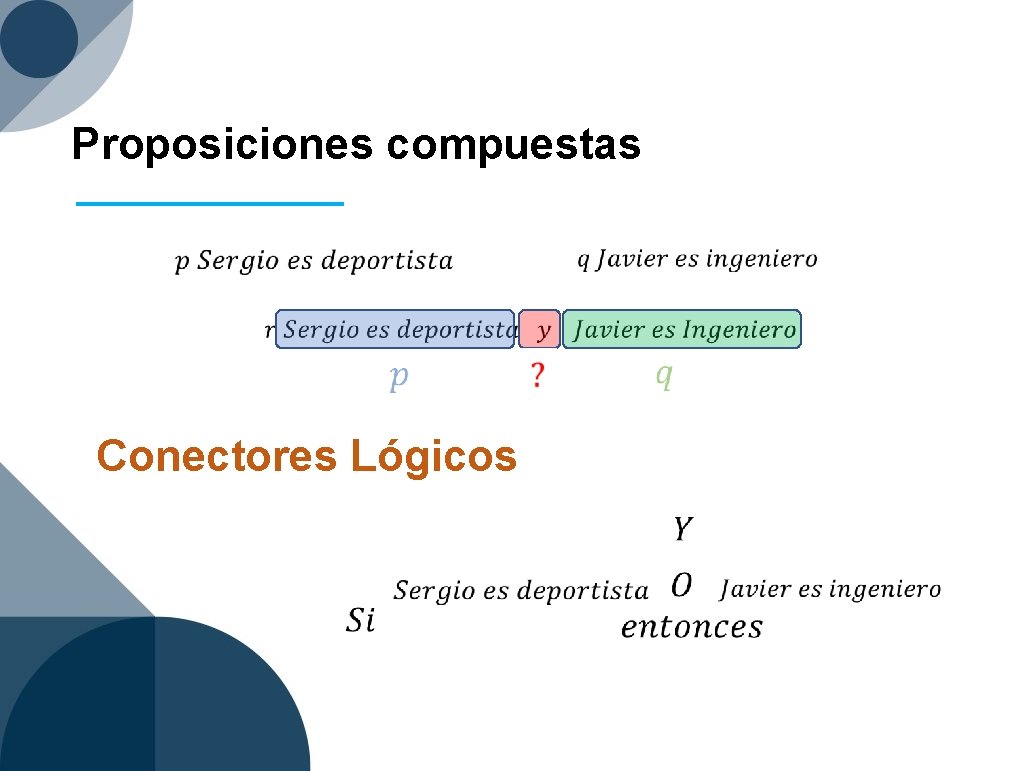
Proposiciones compuestas Conectores Lógicos

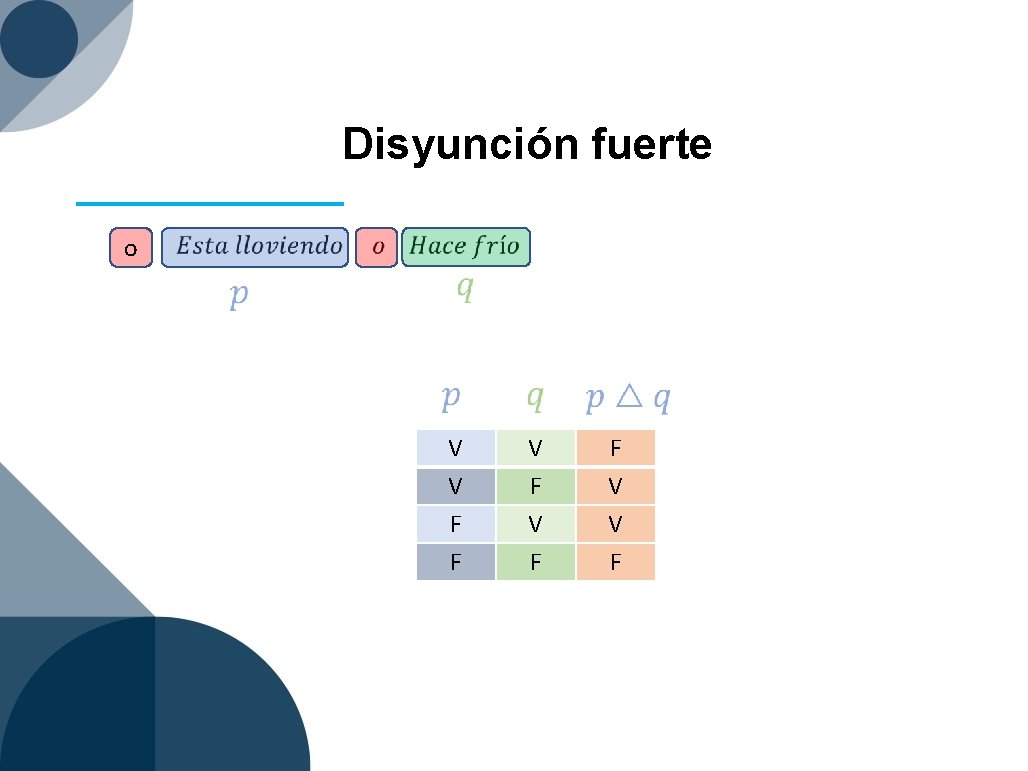
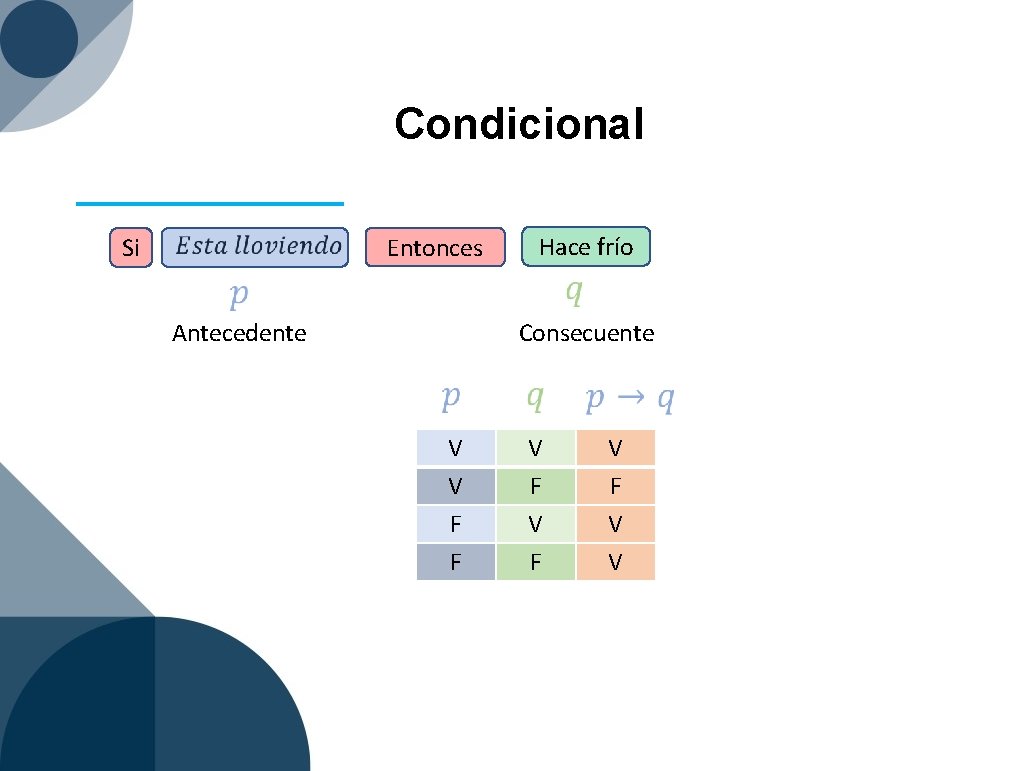
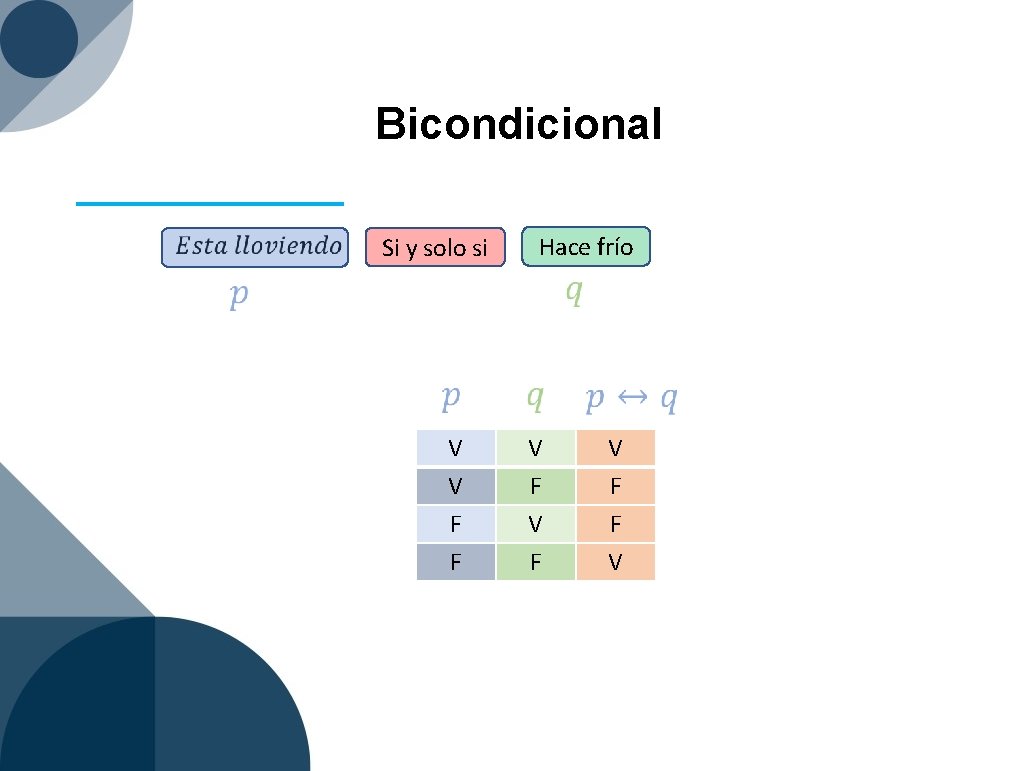
Conectores lógicos Conector lógico y o o…o Si… entonces. . Si y solo si No es verdad Símbolo Nombre Conjunción Disyunción debíl Disyunción fuerte Implicación Equivalencia Negación

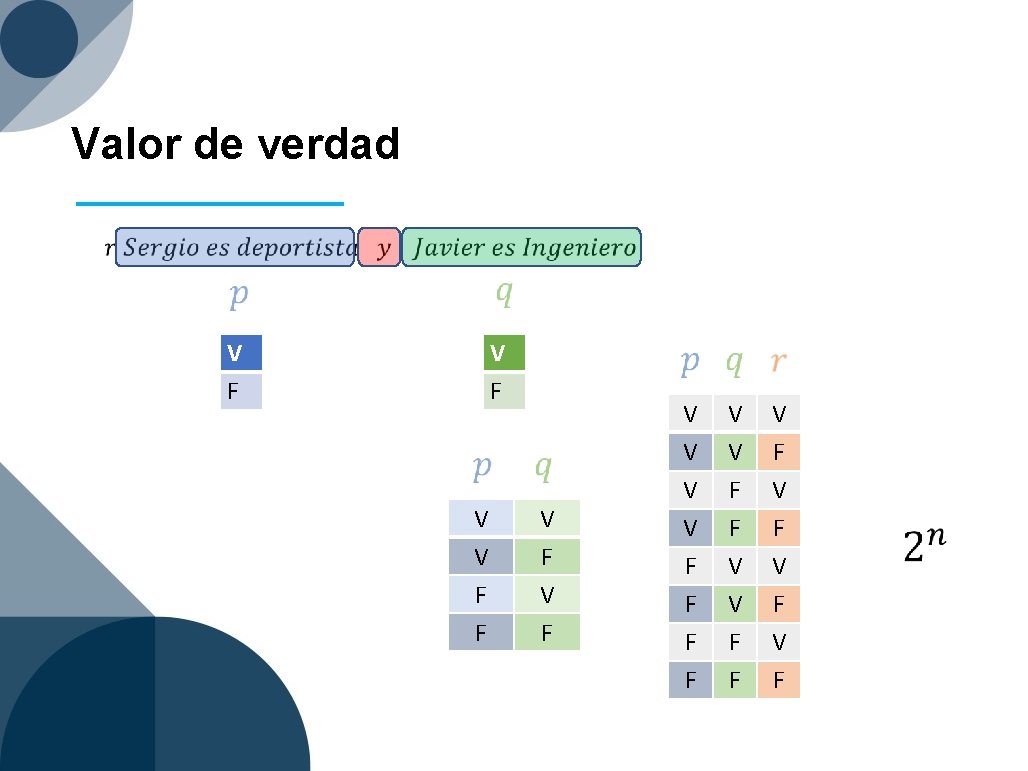
Valor de verdad V F V V F F V F V V F F V F V F

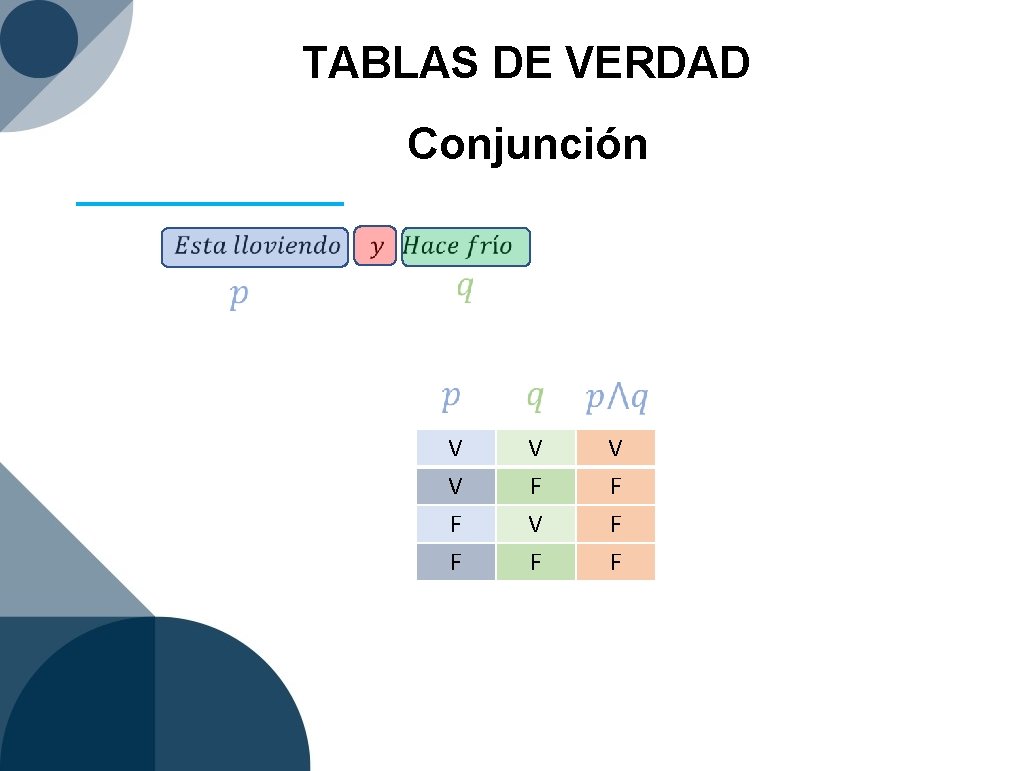
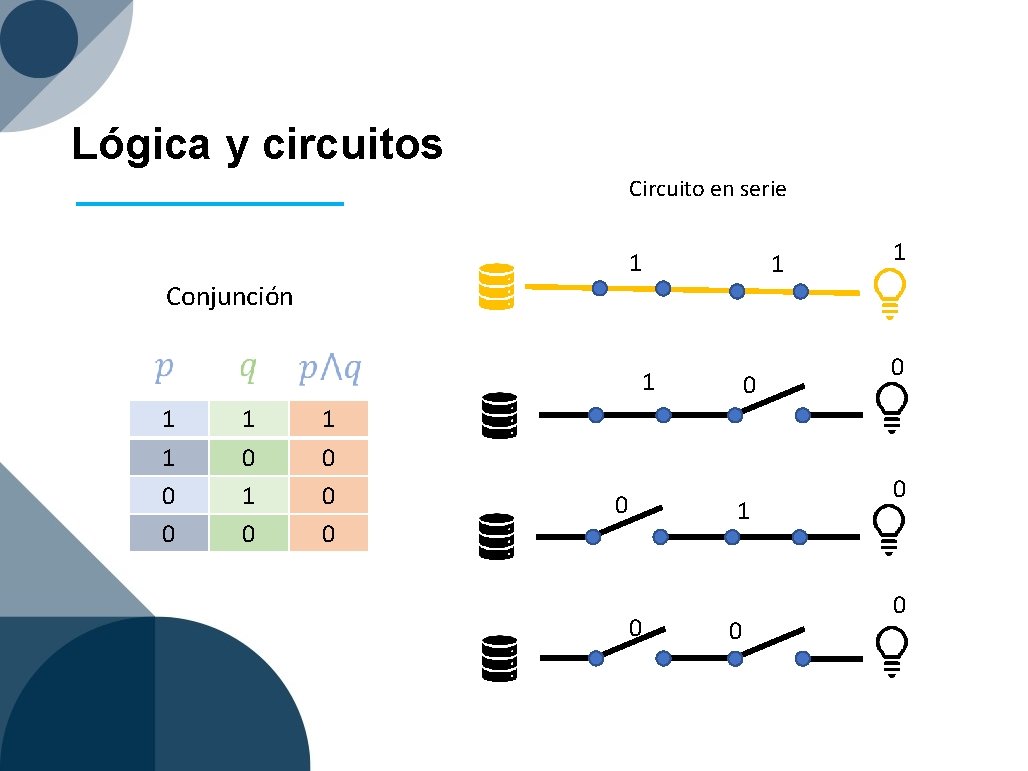
TABLAS DE VERDAD Conjunción V V F F V F V F F F

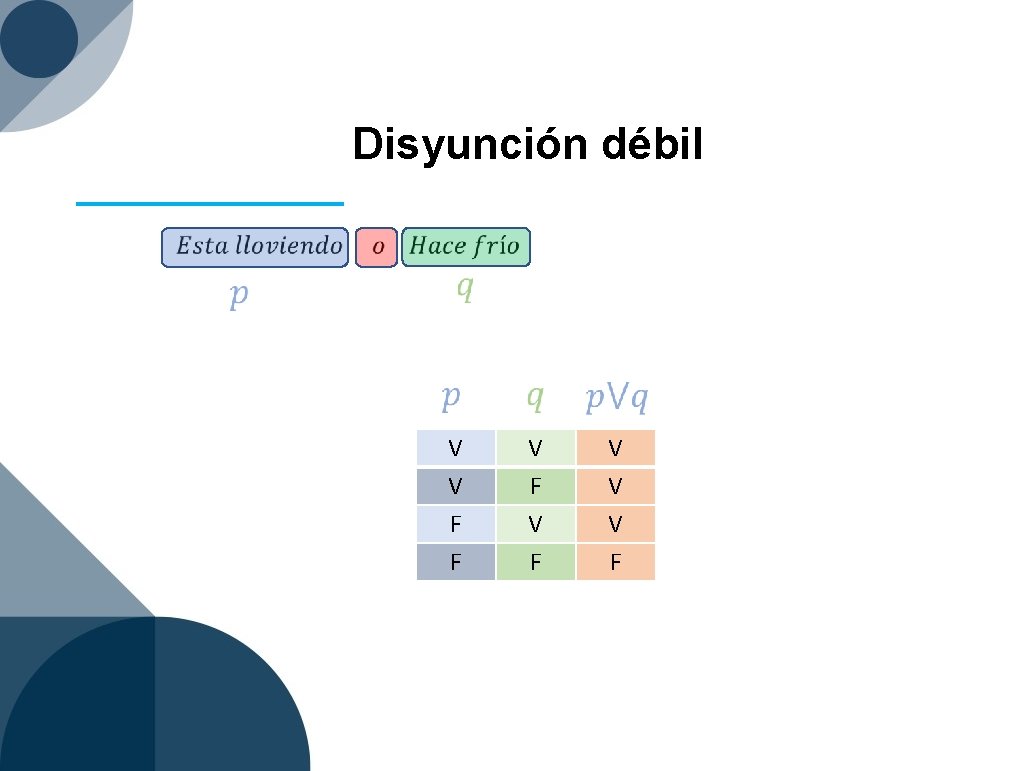
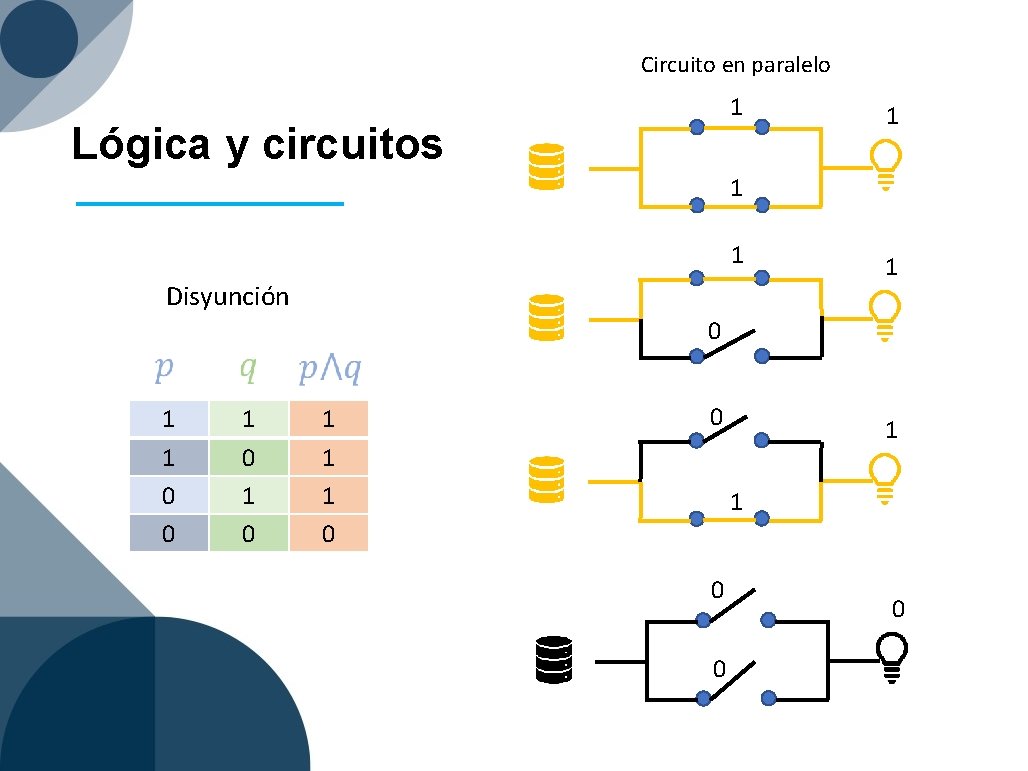
Disyunción débil V V F F V F V V V F

Disyunción fuerte o V V F F V V F

Condicional Si Hace frío Entonces Antecedente Consecuente V V F F V F V V

Bicondicional Hace frío Si y solo si V V F F V F V F F V

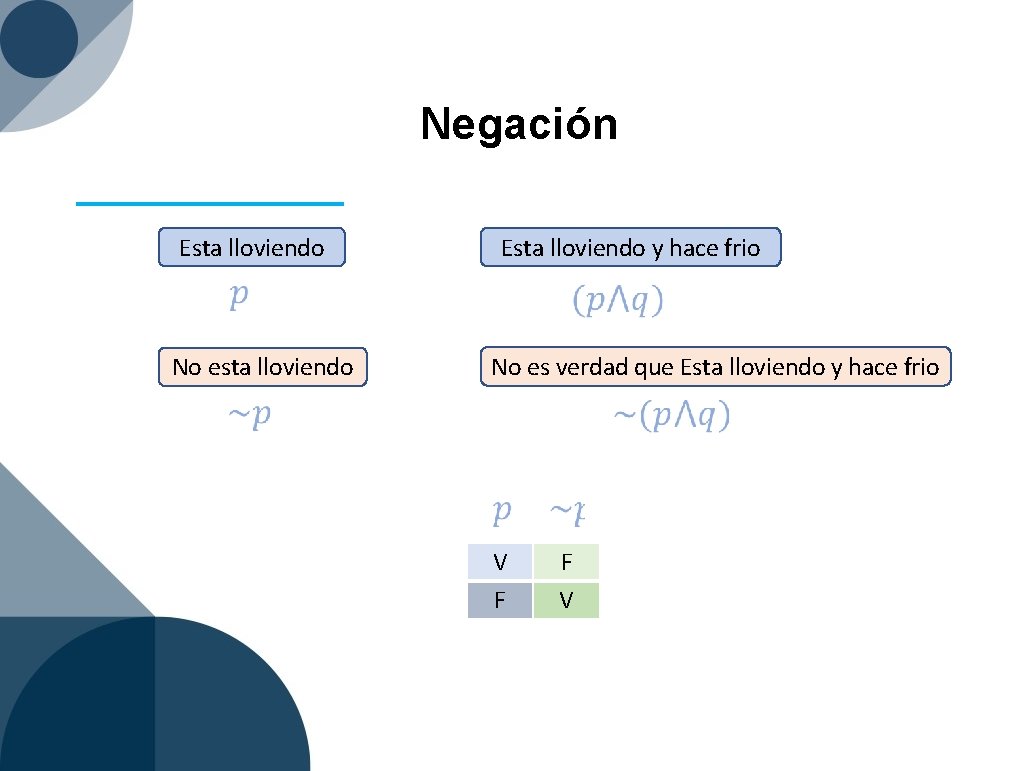
Negación Esta lloviendo No esta lloviendo Esta lloviendo y hace frio No es verdad que Esta lloviendo y hace frio V F F V

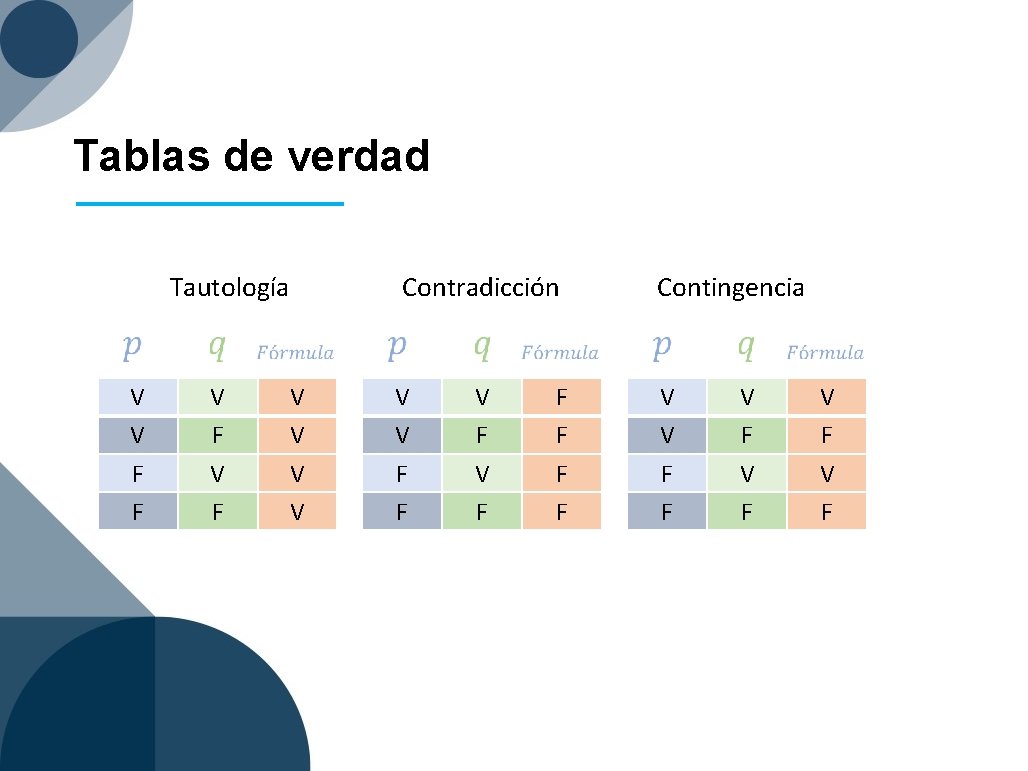
Tablas de verdad Tautología V V F F Contradicción V F V V V F F V F Contingencia F F V V F F V F V F

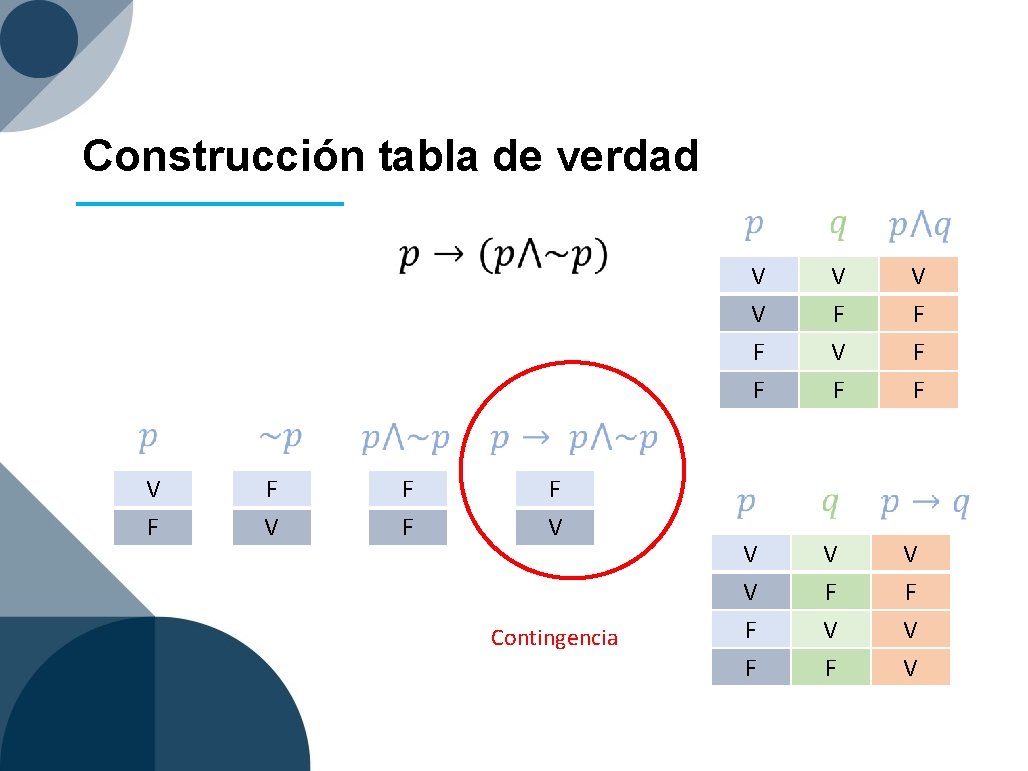
Construcción tabla de verdad V F V V F F V F V F F F F V F F F V Contingencia V V F F V F V V

V V F F V F V V V F F V F V V V V Tautología V V F F V V V F

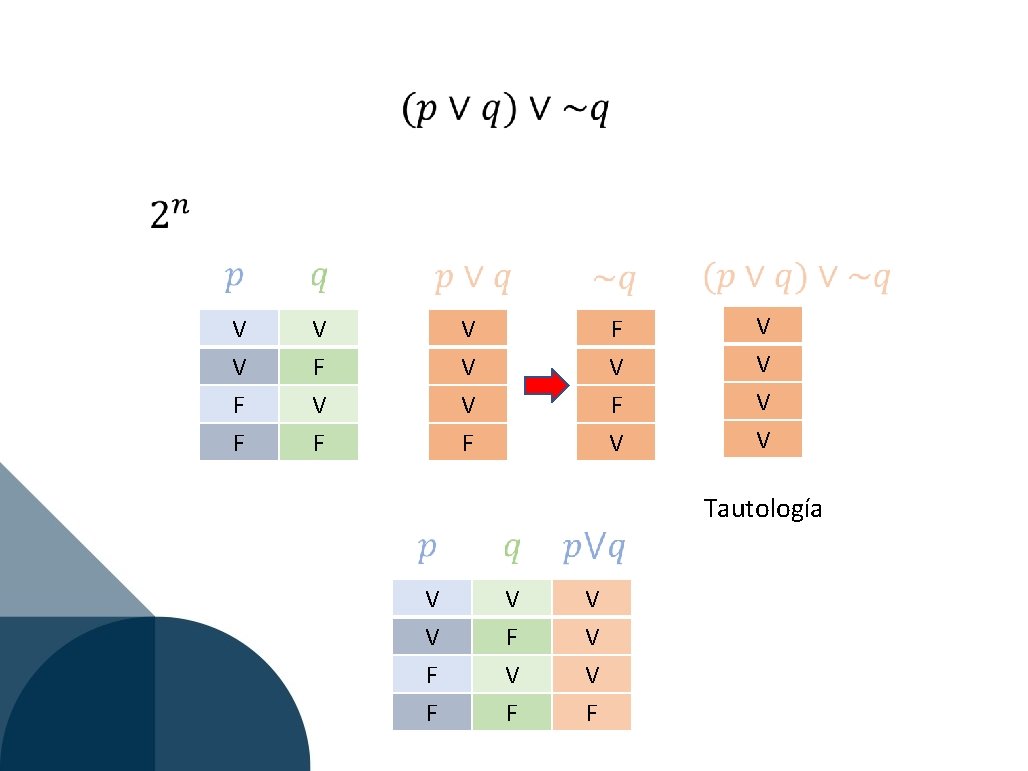
Ejemplo

Ejemplo

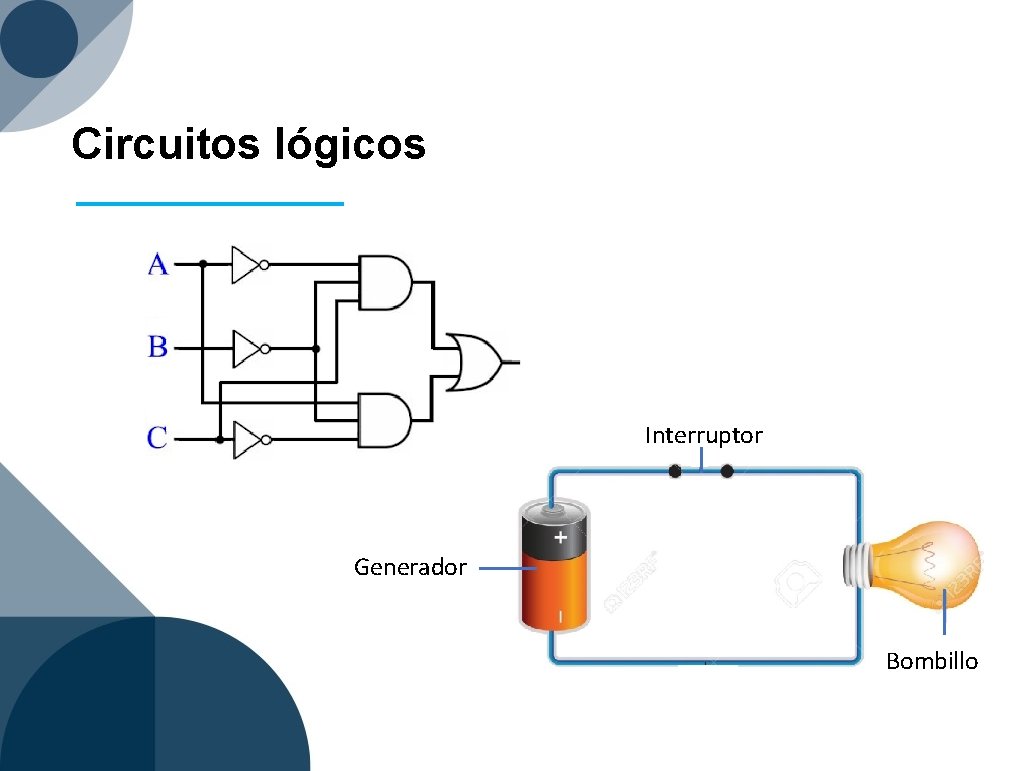
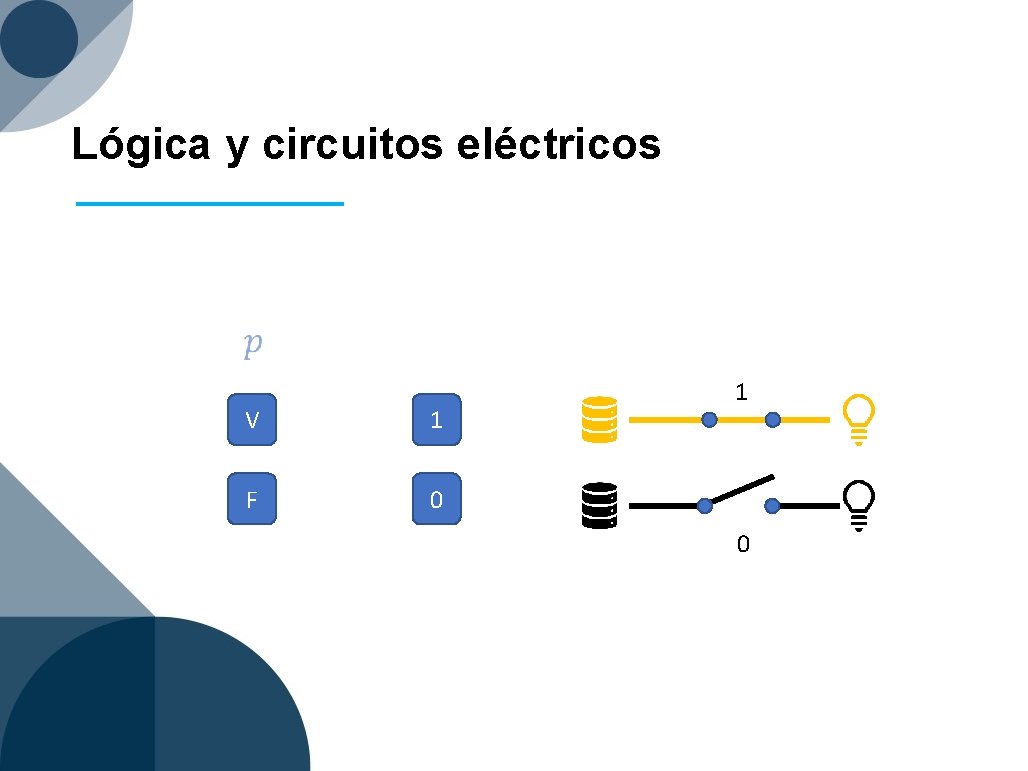
Circuitos lógicos Interruptor Generador Bombillo

Lógica y circuitos eléctricos V 1 F 0 1 0

Lógica y circuitos Circuito en serie 1 1 Conjunción 1 1 0 0 1 0 1 1 0 0 0

Circuito en paralelo 1 Lógica y circuitos 1 1 1 Disyunción 1 1 0 0 0 1 0 1 1 0 0 0

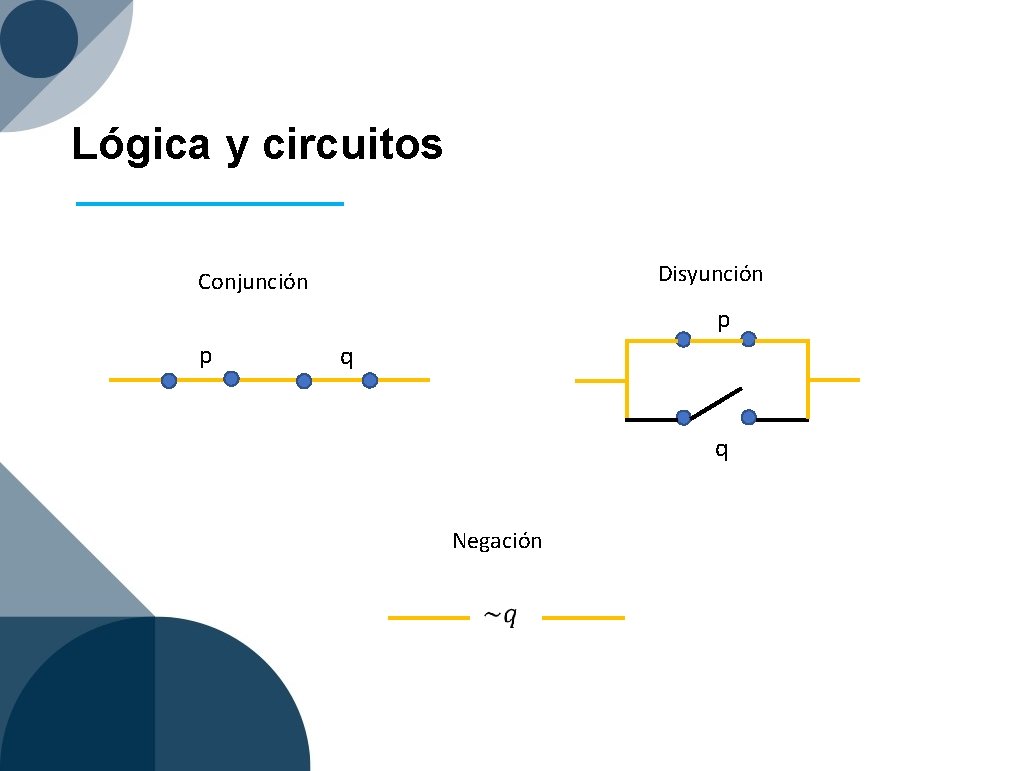
Lógica y circuitos Disyunción Conjunción p p q q Negación

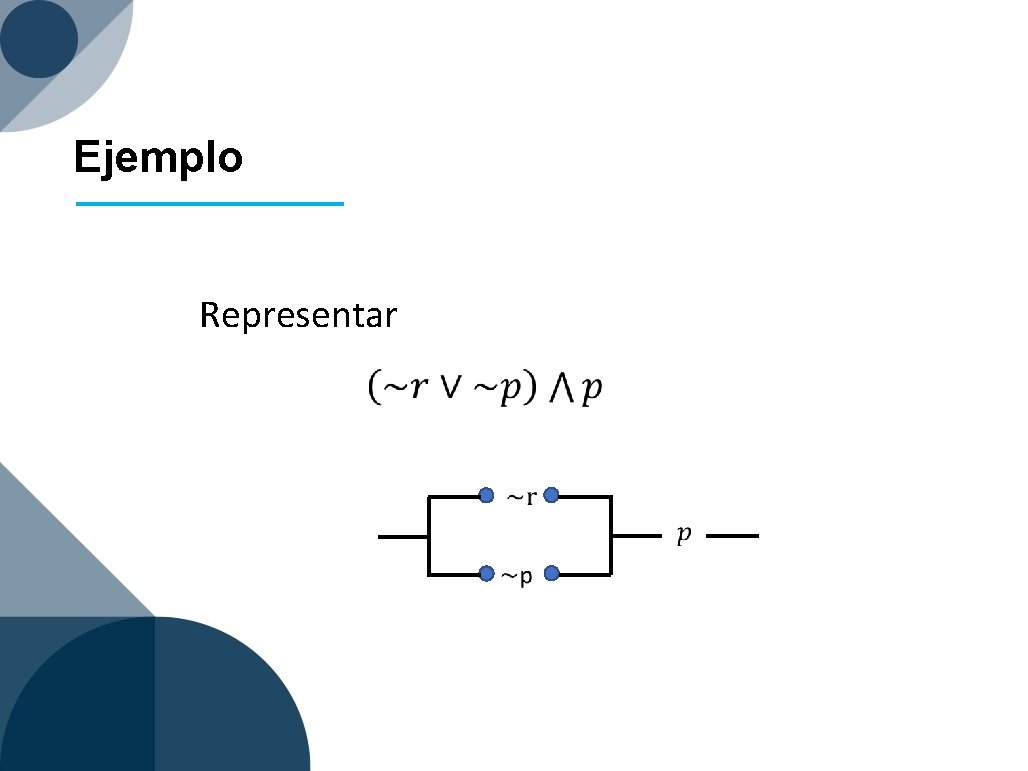
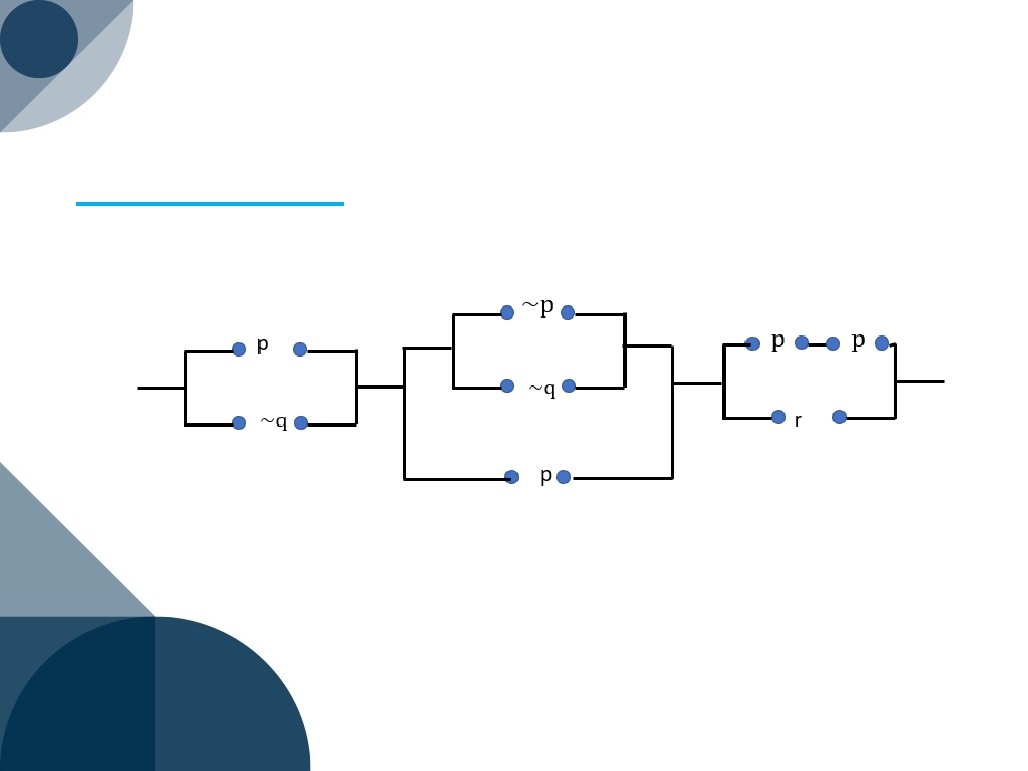
Ejemplo Representar


PARTE 1 TEORIA DE CONJUNTOS

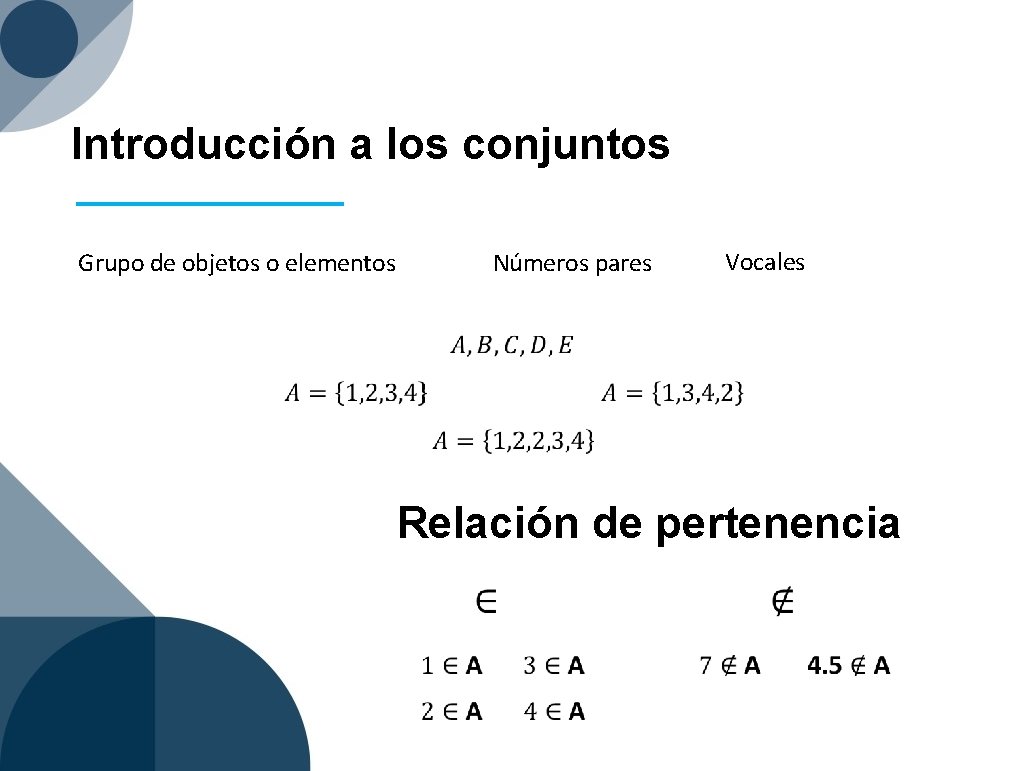
Introducción a los conjuntos Grupo de objetos o elementos Vocales Números pares Relación de pertenencia

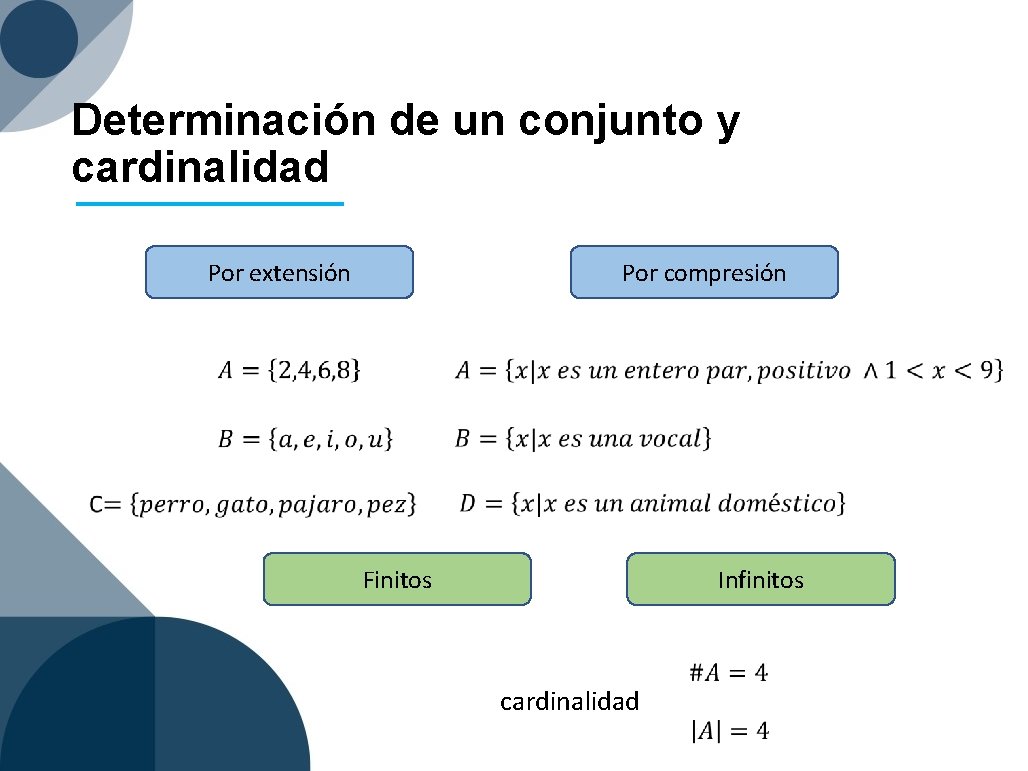
Determinación de un conjunto y cardinalidad Por extensión Por compresión Infinitos Finitos cardinalidad

Subconjuntos

Conjuntos especiales Conjunto nulo Conjunto unitario Conjunto Universal

Operaciones entre conjuntos Resta

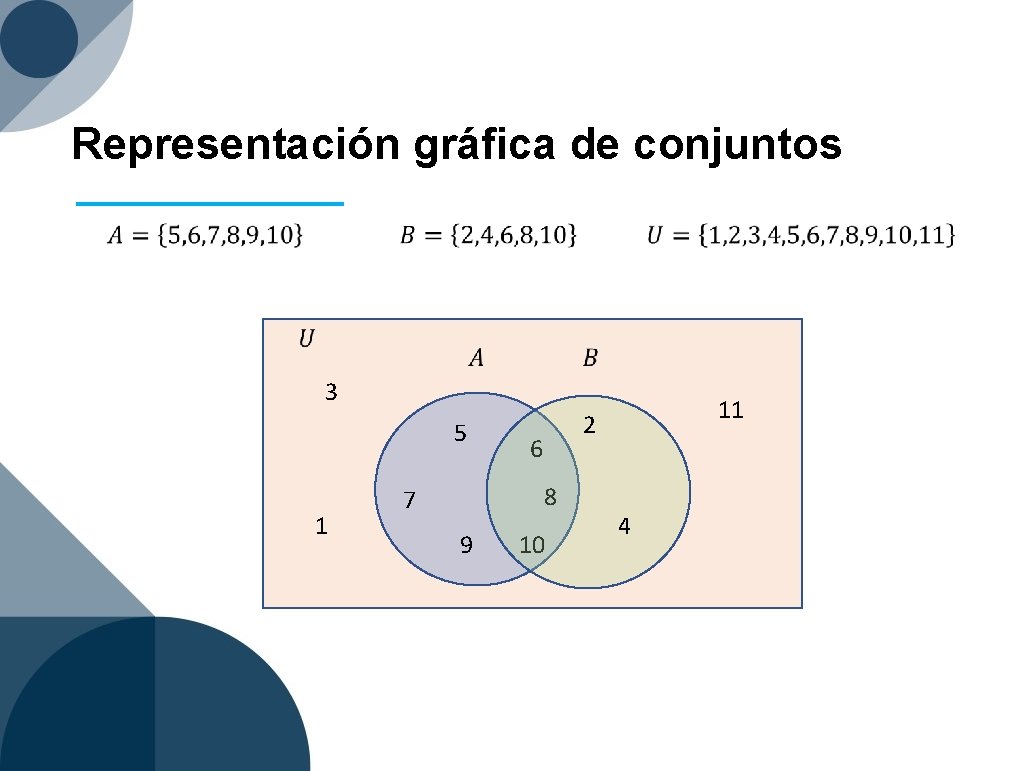
Representación gráfica de conjuntos 3 5 1 2 6 8 7 9 11 10 4

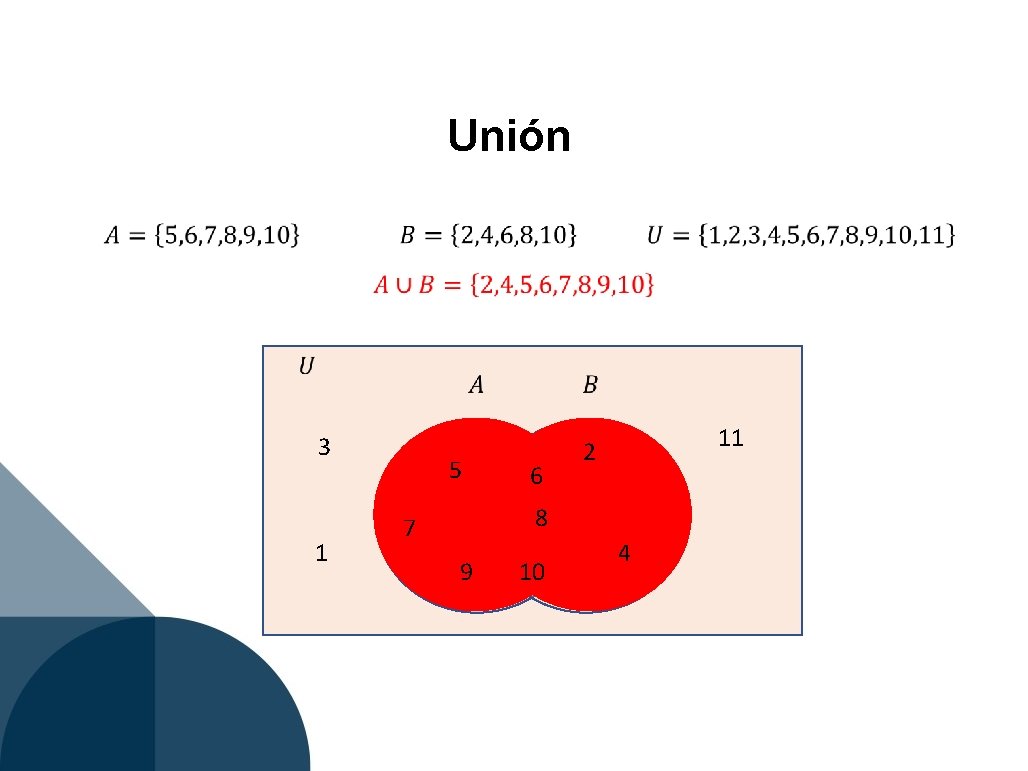
Unión 3 1 5 6 11 2 8 7 9 10 4

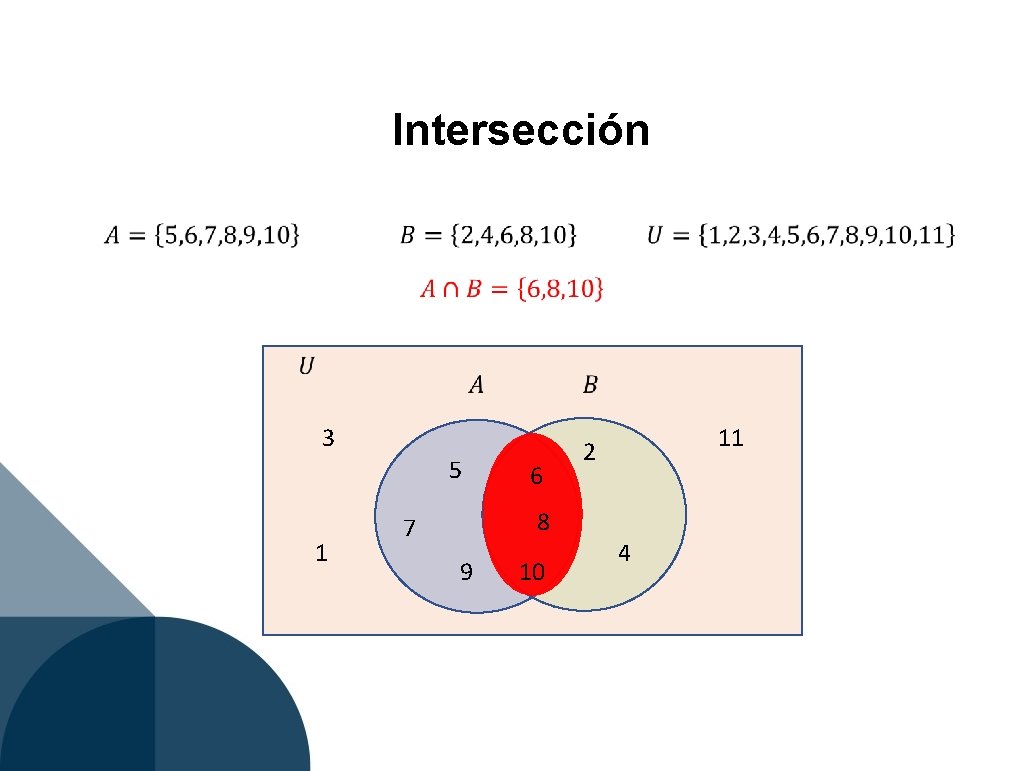
Intersección 3 5 1 6 8 7 9 10 11 2 4

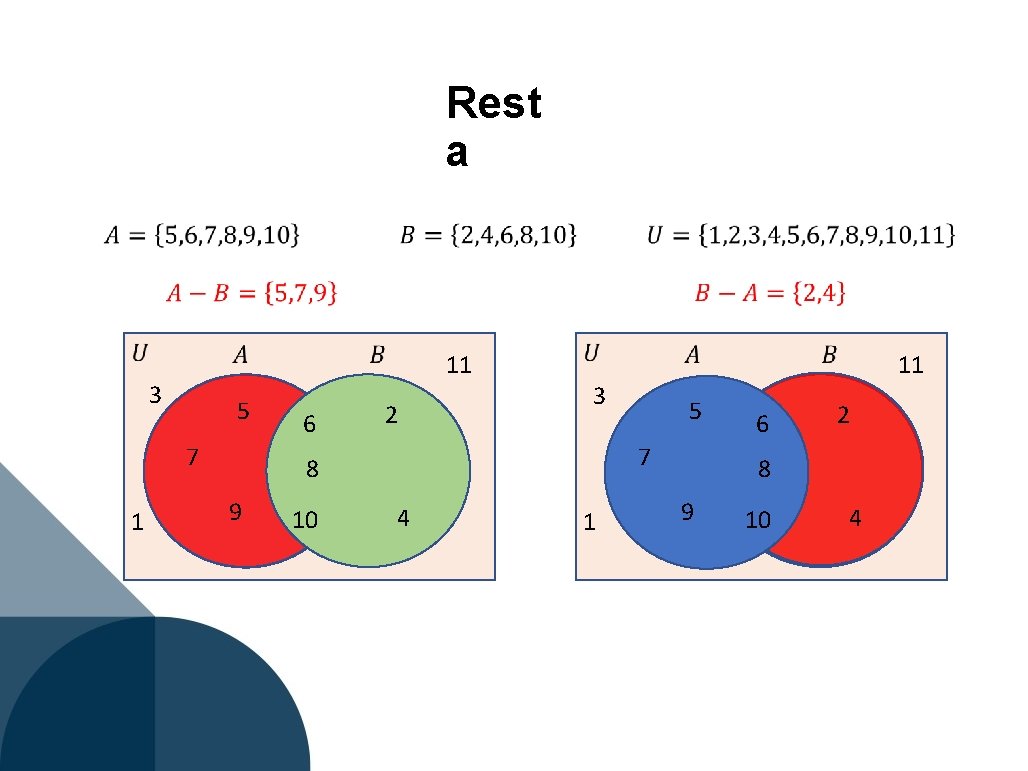
Rest a 3 5 7 1 6 11 2 3 10 5 7 8 9 4 1 6 11 2 8 9 10 4

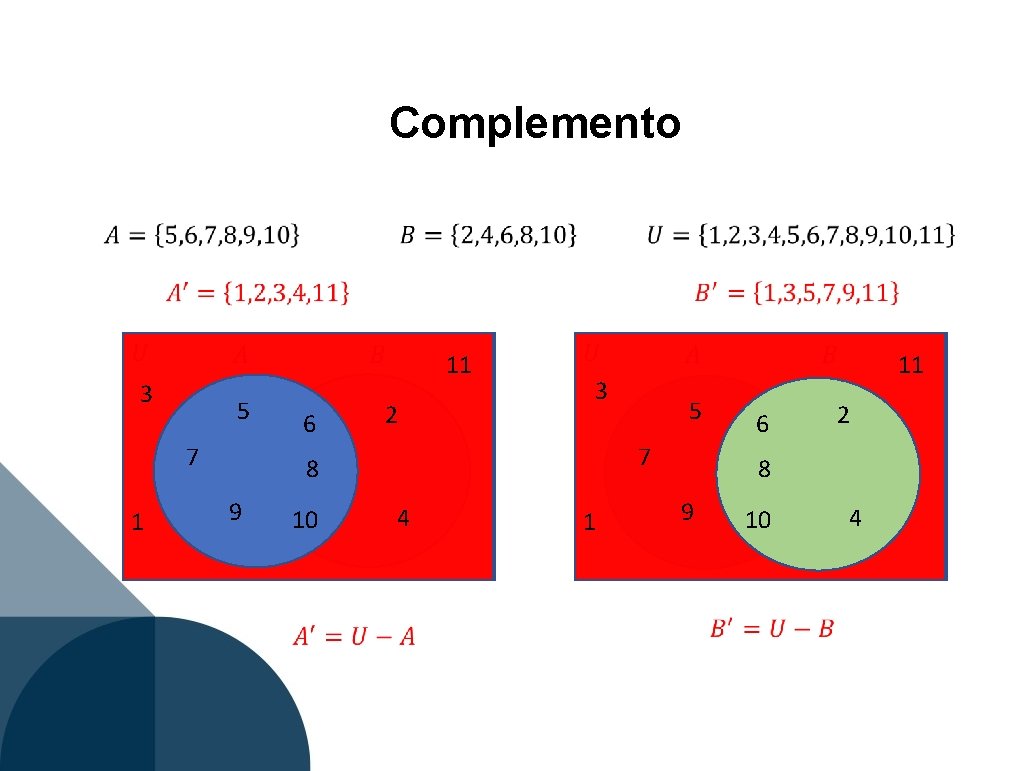
Complemento 3 5 6 7 1 11 2 3 10 5 6 7 8 9 4 1 11 2 8 9 10 4

Algunas propiedades

PARTE 3 TEORÍA DE GRÁFICAS

Grafos Módelos matemáticos que sirven para representar las relaciones entre objetos de un conjunto

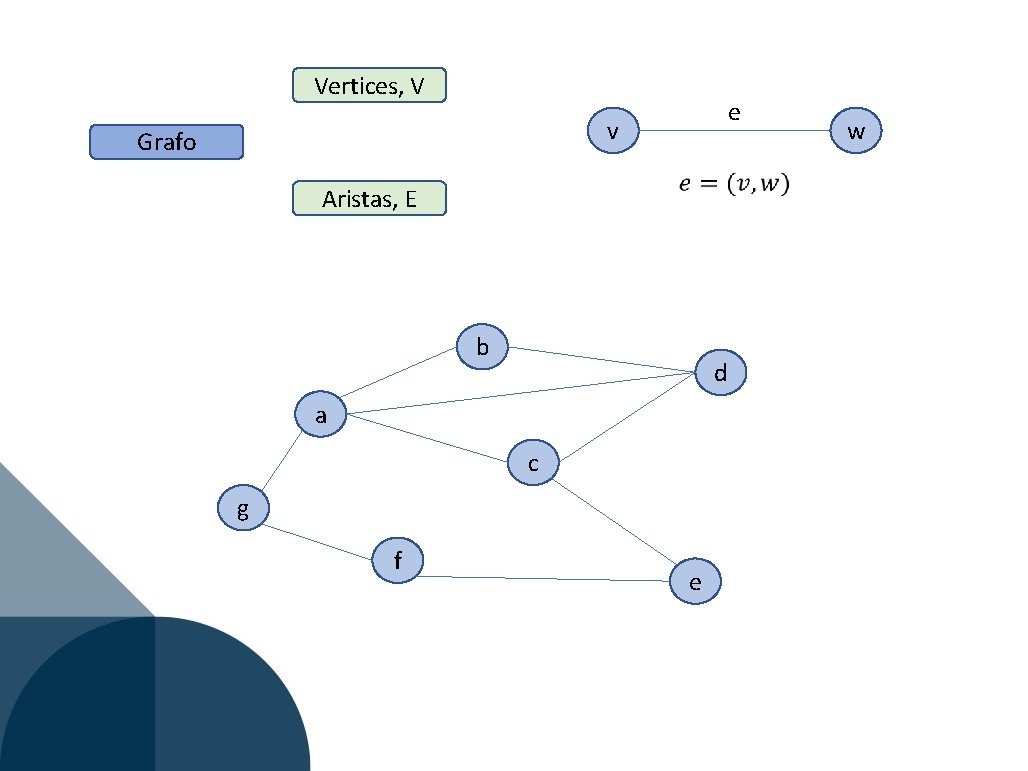
Vertices, V e v Grafo Aristas, E b d a c g f e w

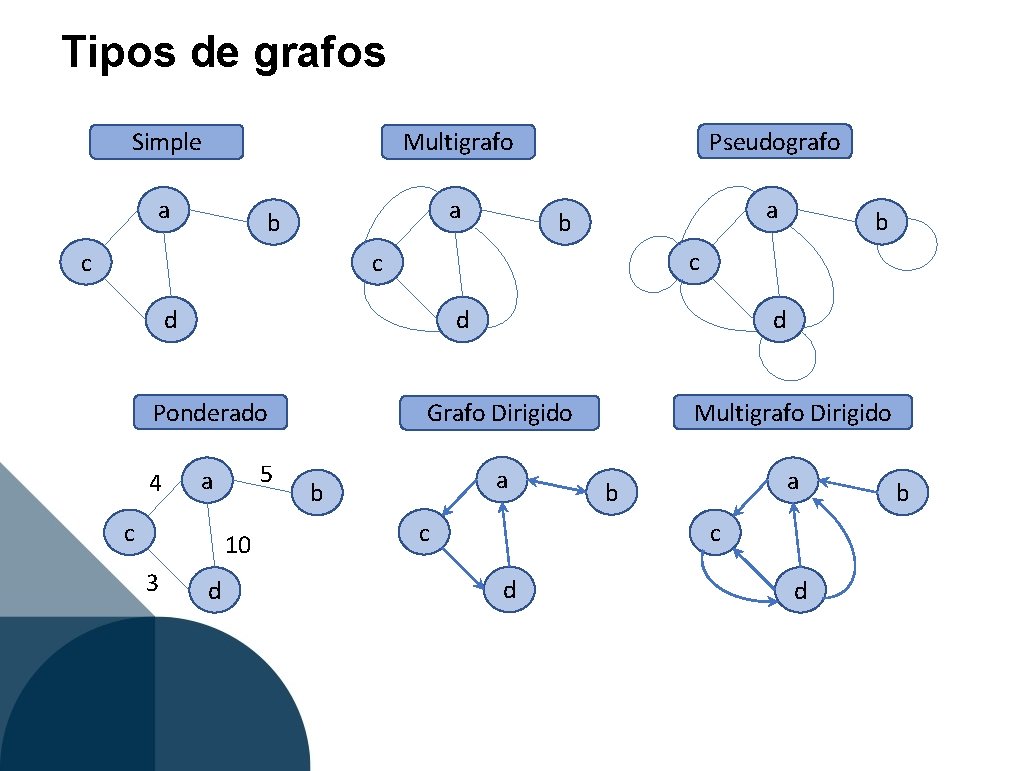
Tipos de grafos Simple Pseudografo Multigrafo a a b c c d 4 5 a c 10 3 d d Ponderado d b Multigrafo Dirigido Grafo Dirigido a b c d d b

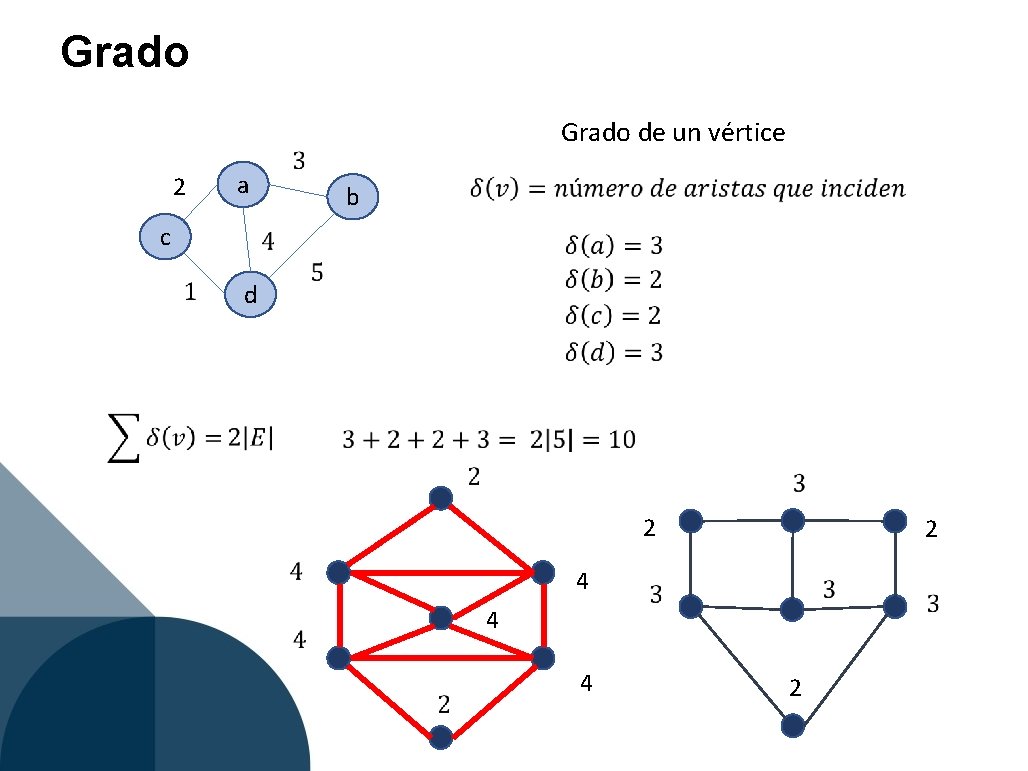
Grado 2 a c Grado de un vértice b d 2 4 4 4 2 2

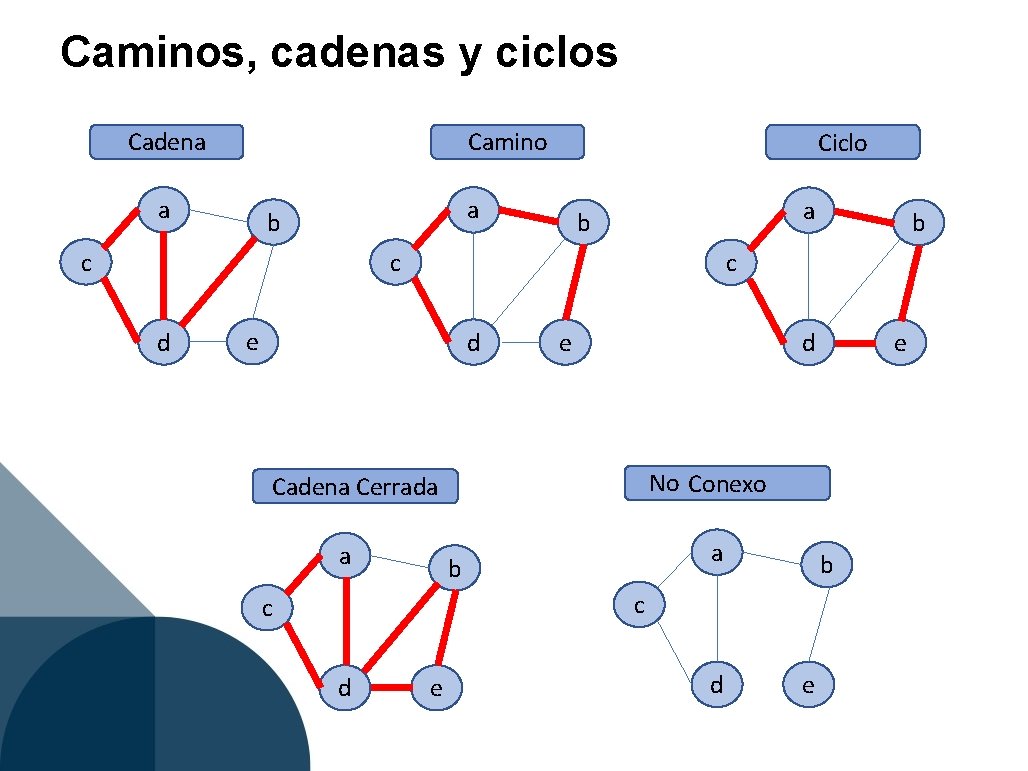
Caminos, cadenas y ciclos Cadena Camino a Ciclo a b c d c e d a a b b c c e e No Conexo Cadena Cerrada d b d e

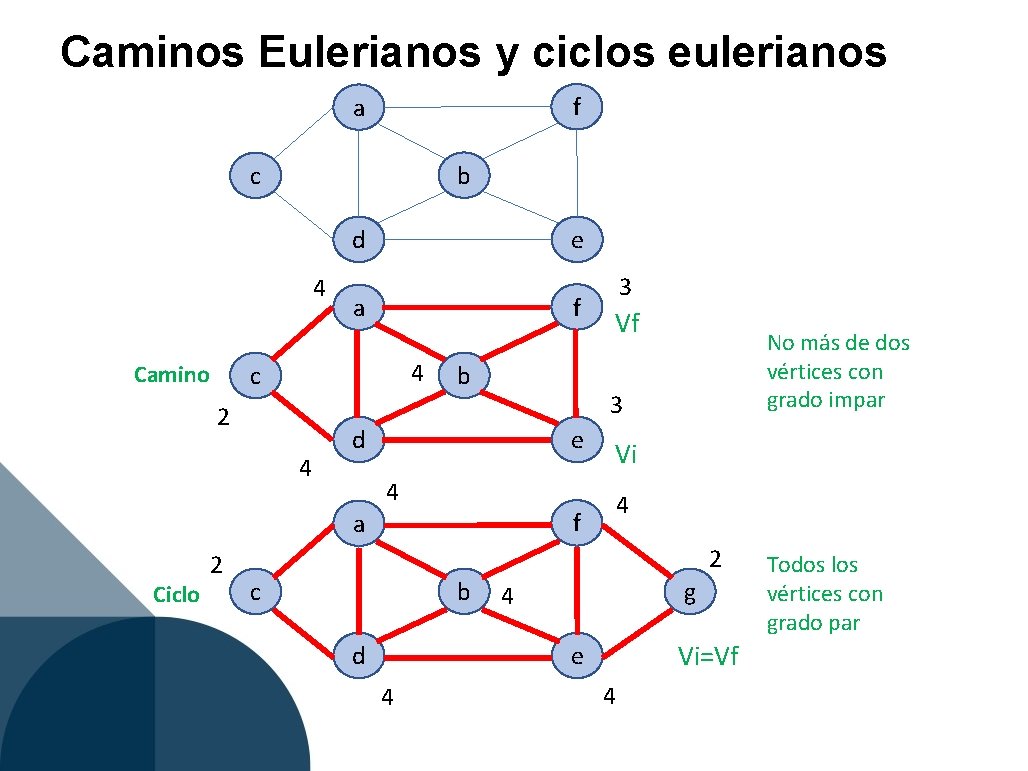
Caminos Eulerianos y ciclos eulerianos f a b c d 4 Camino e f a 4 c 2 4 b Ciclo Vf No más de dos vértices con grado impar 3 d e 4 f a 2 3 Vi 4 2 b c d g 4 Vi=Vf e 4 4 Todos los vértices con grado par

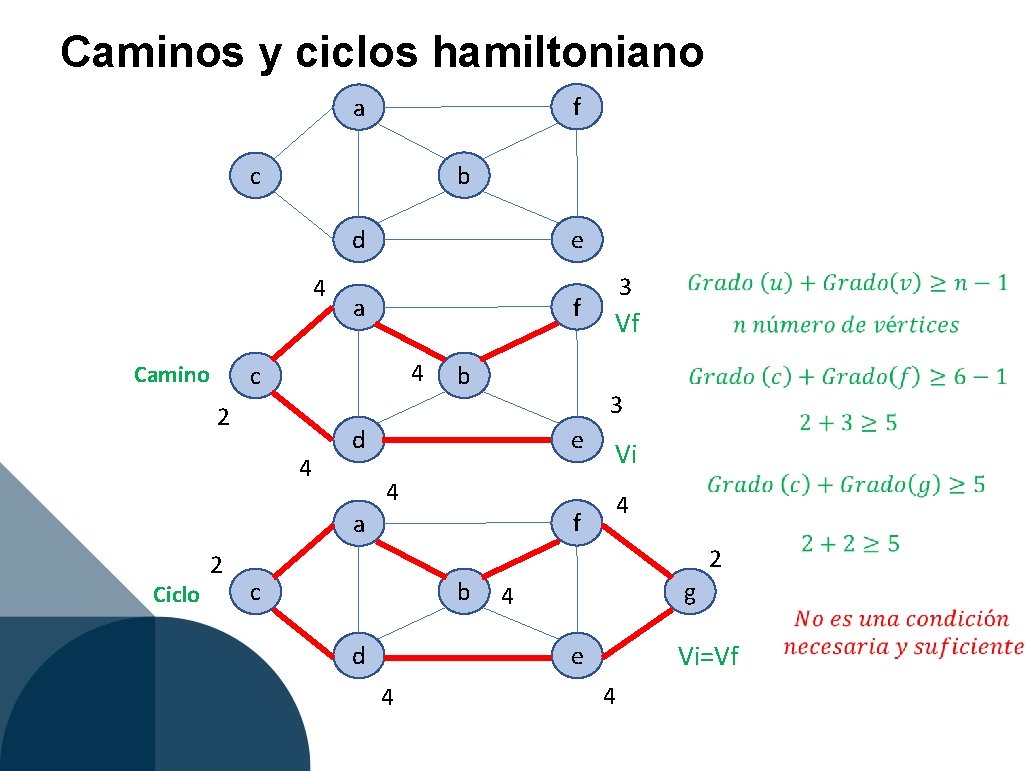
Caminos y ciclos hamiltoniano f a b c d 4 Camino e f a 4 c 2 4 b Ciclo d e 4 f b c d Vf 3 a 2 3 Vi 4 2 g 4 Vi=Vf e 4 4

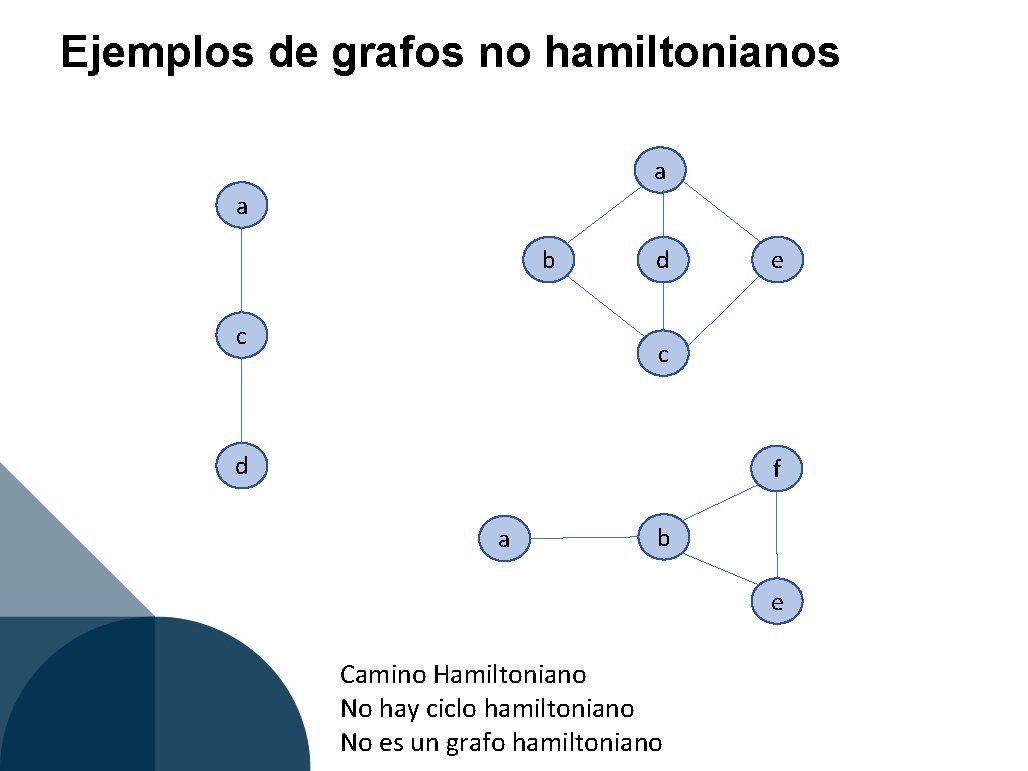
Ejemplos de grafos no hamiltonianos a a b c d e c d f a b e Camino Hamiltoniano No hay ciclo hamiltoniano No es un grafo hamiltoniano

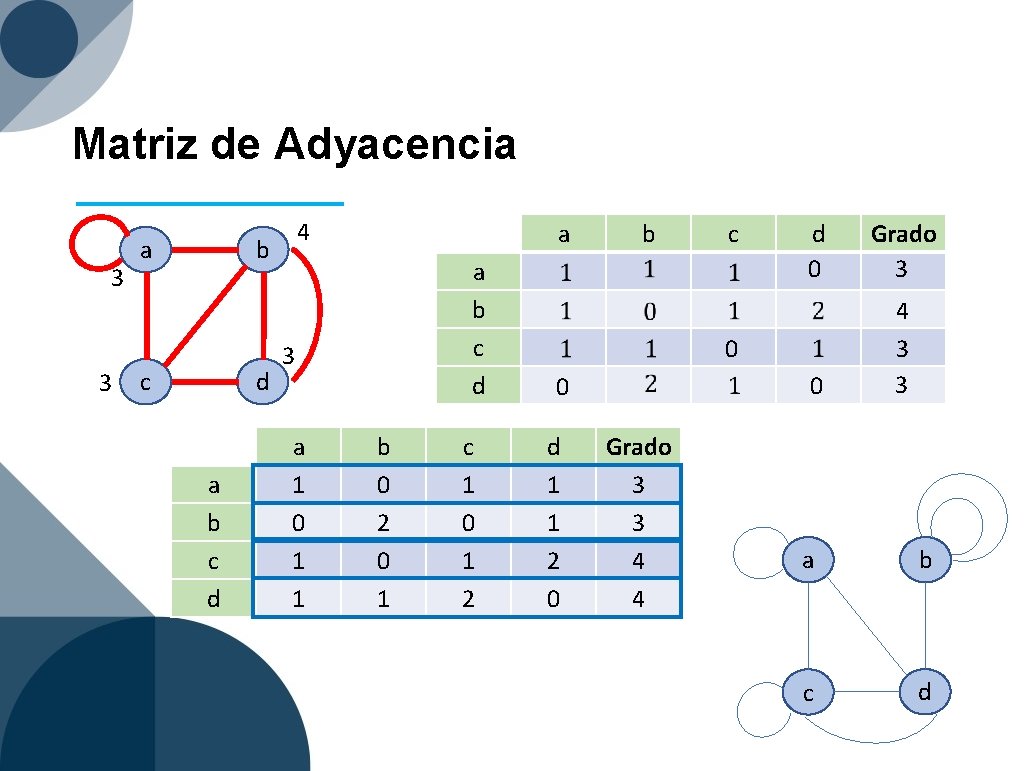
Matriz de Adyacencia 3 3 a 4 b d c a b c d a a b c d 3 a 1 0 1 1 b 0 2 0 1 c 1 0 1 2 0 d 1 1 2 0 b Grado 3 3 4 4 c 0 d 0 Grado 3 0 4 3 3 a b c d

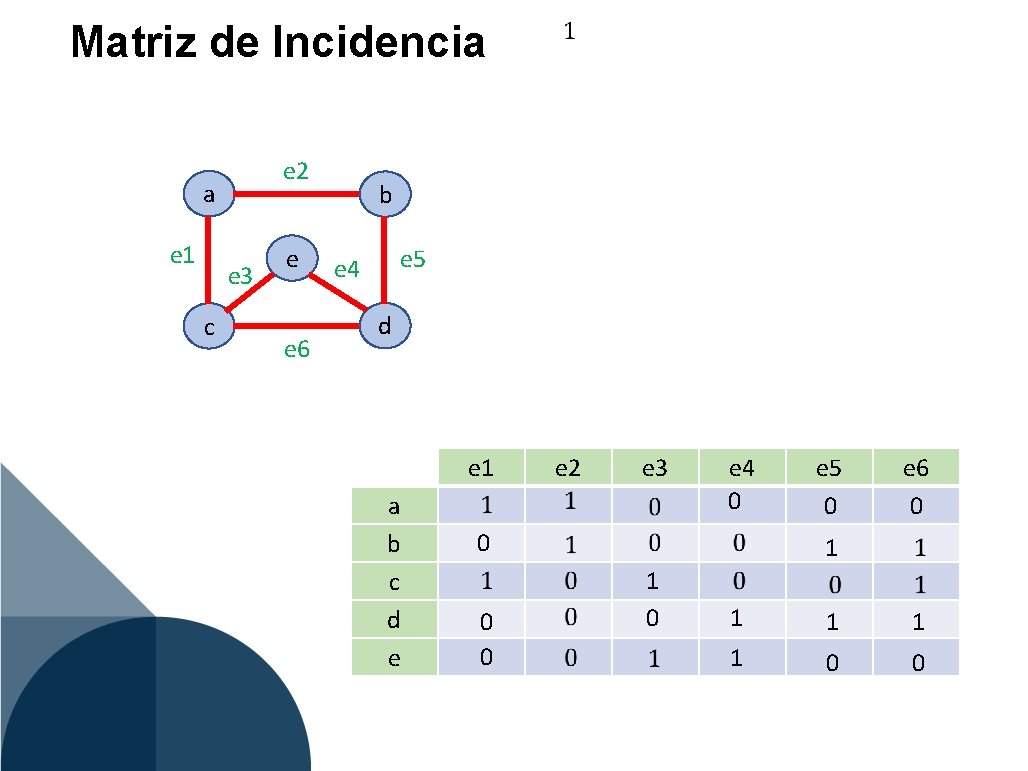
Matriz de Incidencia e 2 a e 1 e 3 c e e 6 b e 5 e 4 d e 1 a b c d e 0 0 0 e 2 e 3 1 0 e 4 0 e 5 0 e 6 0 1 1 1 0 0

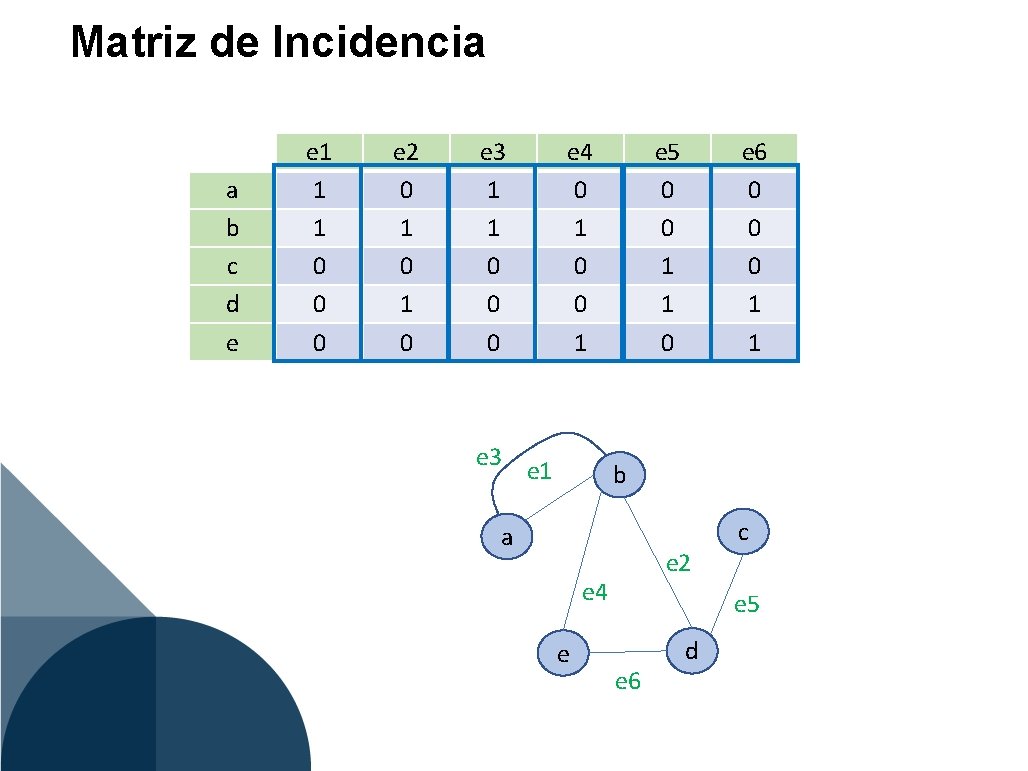
Matriz de Incidencia a b c d e e 1 1 1 0 0 0 e 2 0 1 0 e 3 1 1 0 0 0 e 3 e 4 0 1 0 0 1 e 5 0 0 1 1 0 e 6 0 0 0 1 1 b a e 2 e 4 e c e 5 e 6 d

Ejercicio matriz de adyacencia e incidencia

PARTE 4 ARBOLES

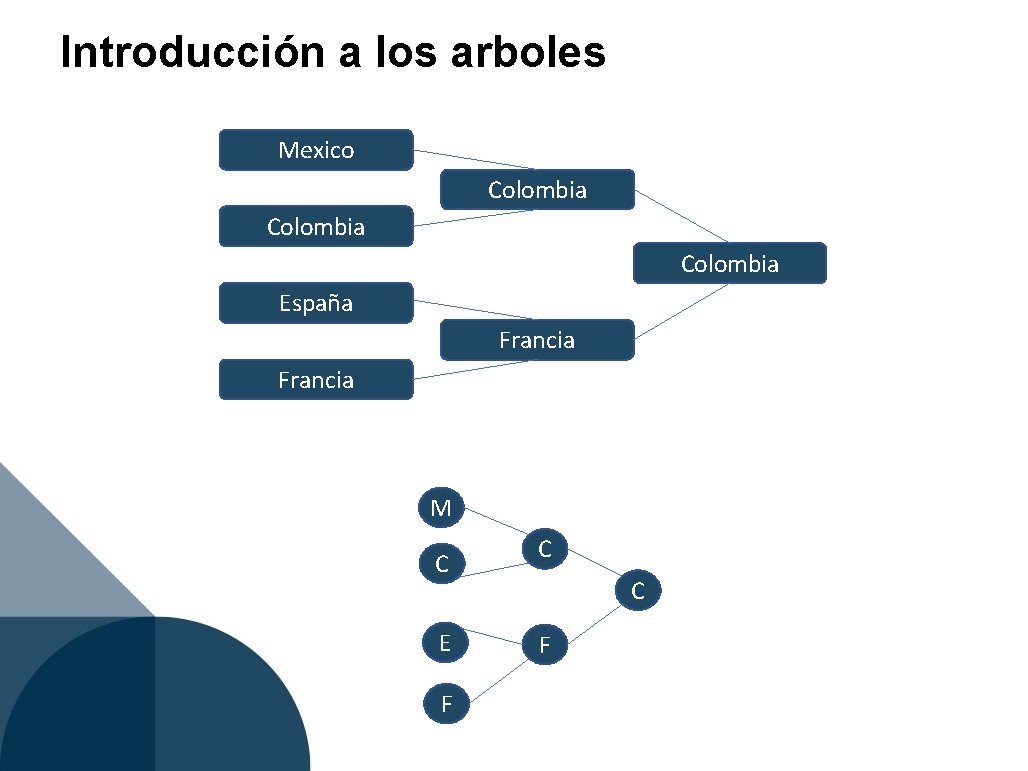
Introducción a los arboles Mexico Colombia España Francia M C E F C C F

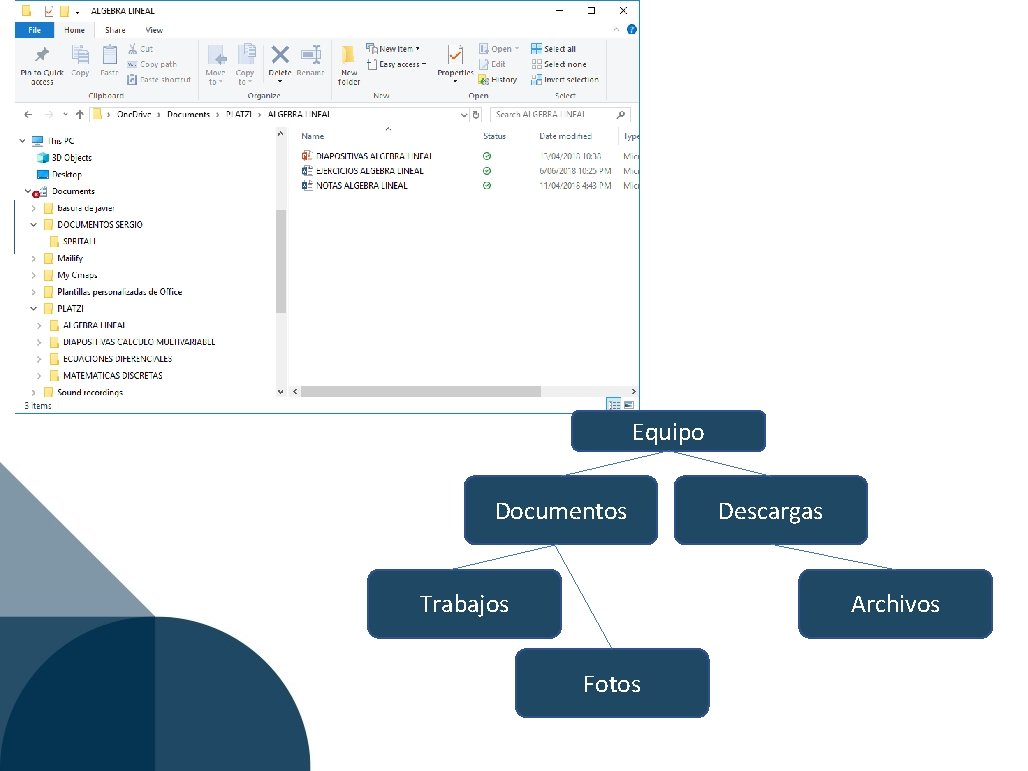
Presidente Vicepresidente Académico Docente Cátedra Vicepresidente Administrativo Personal Docente Plante Equipo Documentos Trabajos Descargas Archivos Fotos

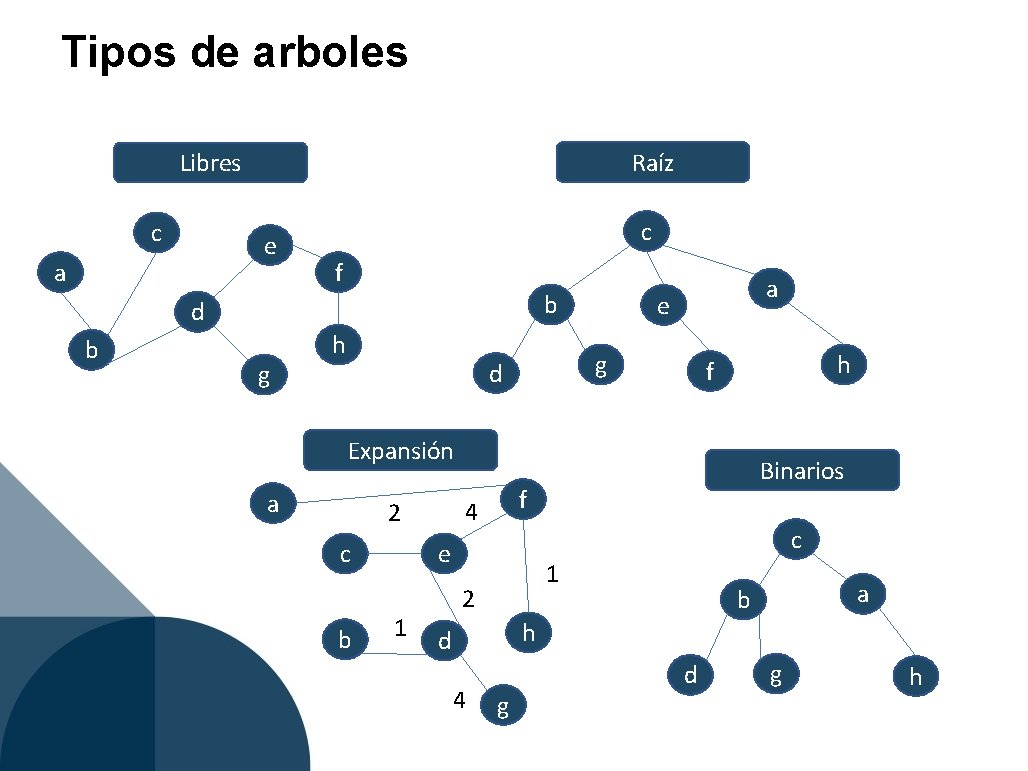
Tipos de arboles Raíz Libres c e a c f b d b g h a e g d h f Expansión a c b f 4 2 c e 1 Binarios 1 2 a b h d 4 g d g h

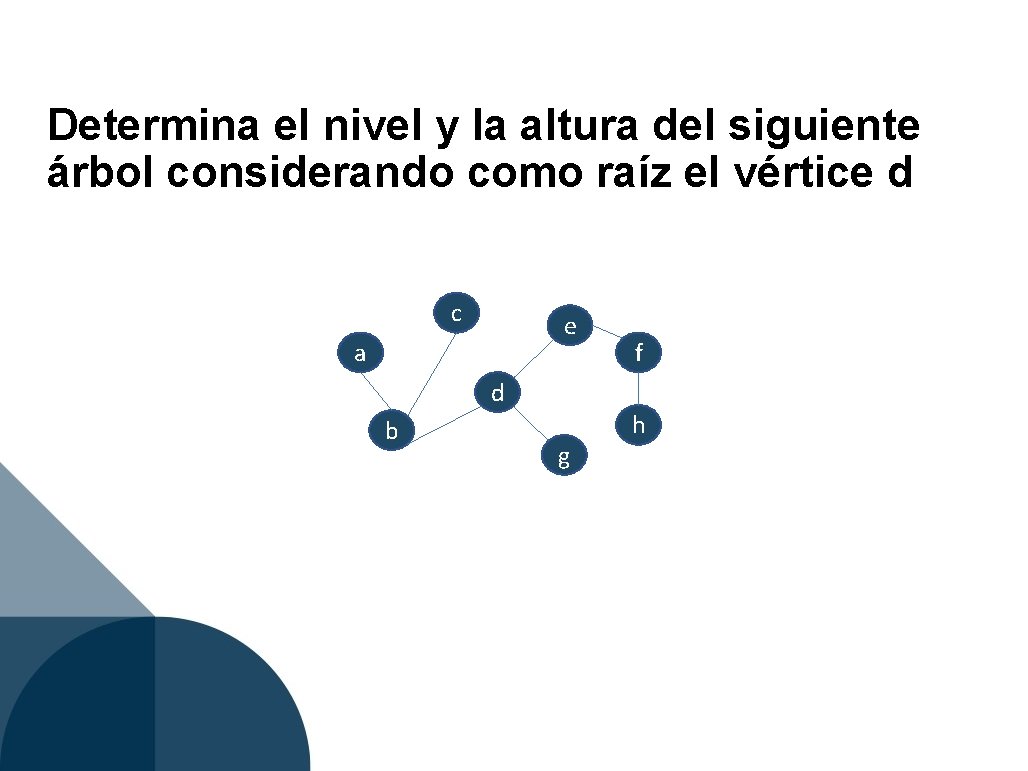
Determina el nivel y la altura del siguiente árbol considerando como raíz el vértice d c e a f d b g h

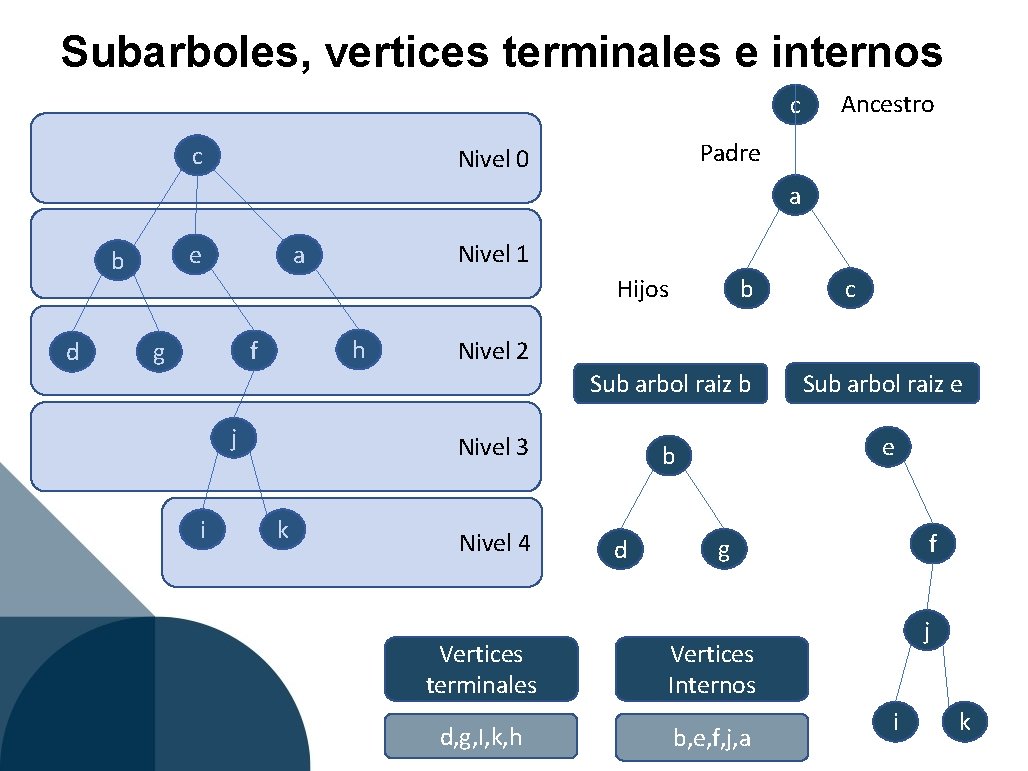
Subarboles, vertices terminales e internos c c Ancestro Padre Nivel 0 a e b d Nivel 1 a Hijos h f g j i c Nivel 2 Sub arbol raiz b Sub arbol raiz e b e Nivel 3 k b Nivel 4 Vertices terminales d, g, I, k, h d f g j Vertices Internos b, e, f, j, a i k

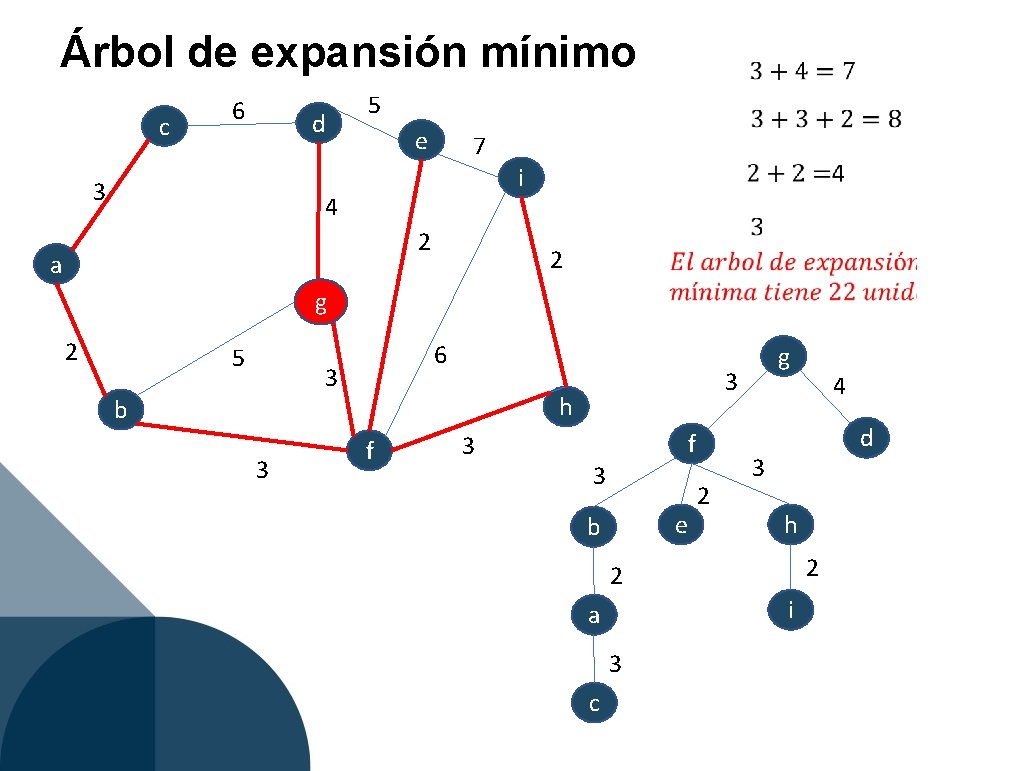
Árbol de expansión mínimo c 6 d 3 5 e 7 i 4 2 a 2 gg 2 5 6 3 3 3 h b f 3 g f 3 e b 2 d 3 h 2 2 i a 3 c 4

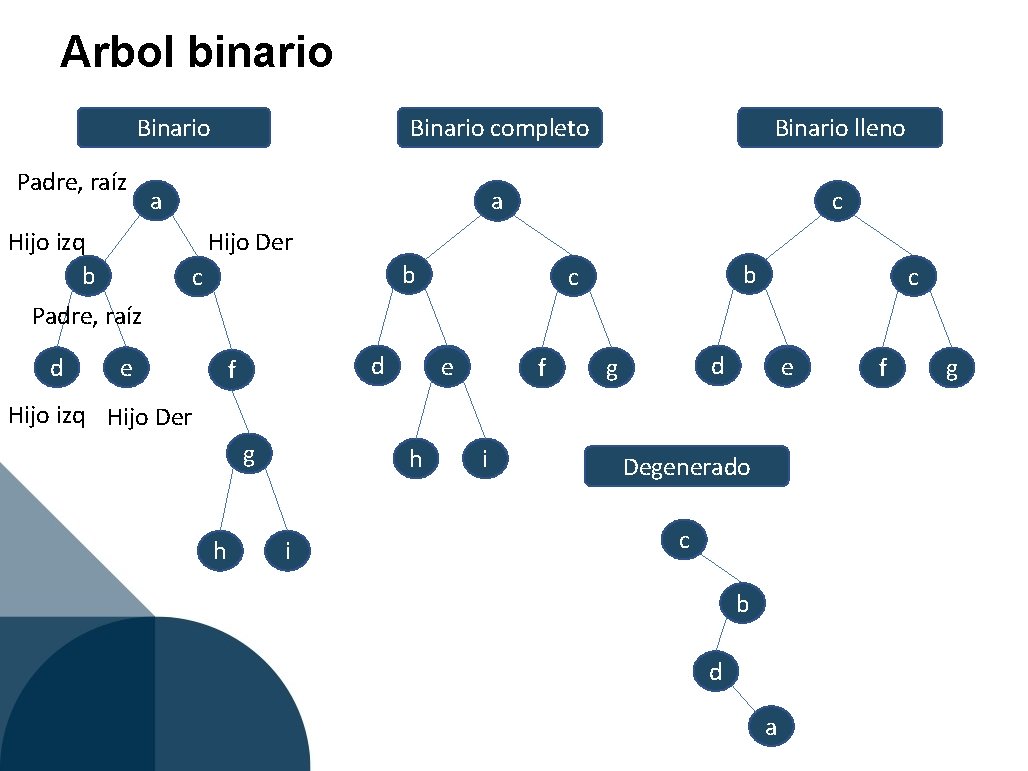
Arbol binario Binario Padre, raíz Binario completo Binario lleno a c a Hijo izq b Hijo Der b c c Padre, raíz d e d f eg f d g eg Hijo izq Hijo Der g h h i i Degenerado c b d a f g

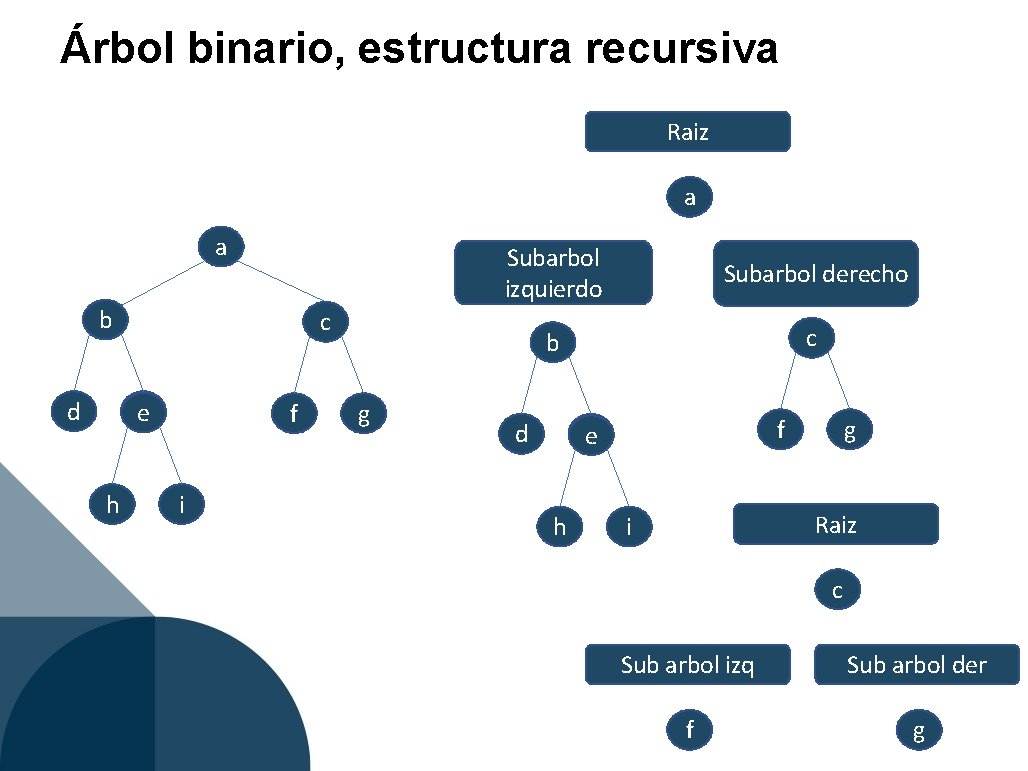
Árbol binario, estructura recursiva Raiz a a b d Subarbol derecho b c c eg h Subarbol izquierdo f i g d f eg h g Raiz i c Sub arbol izq Sub arbol der f g

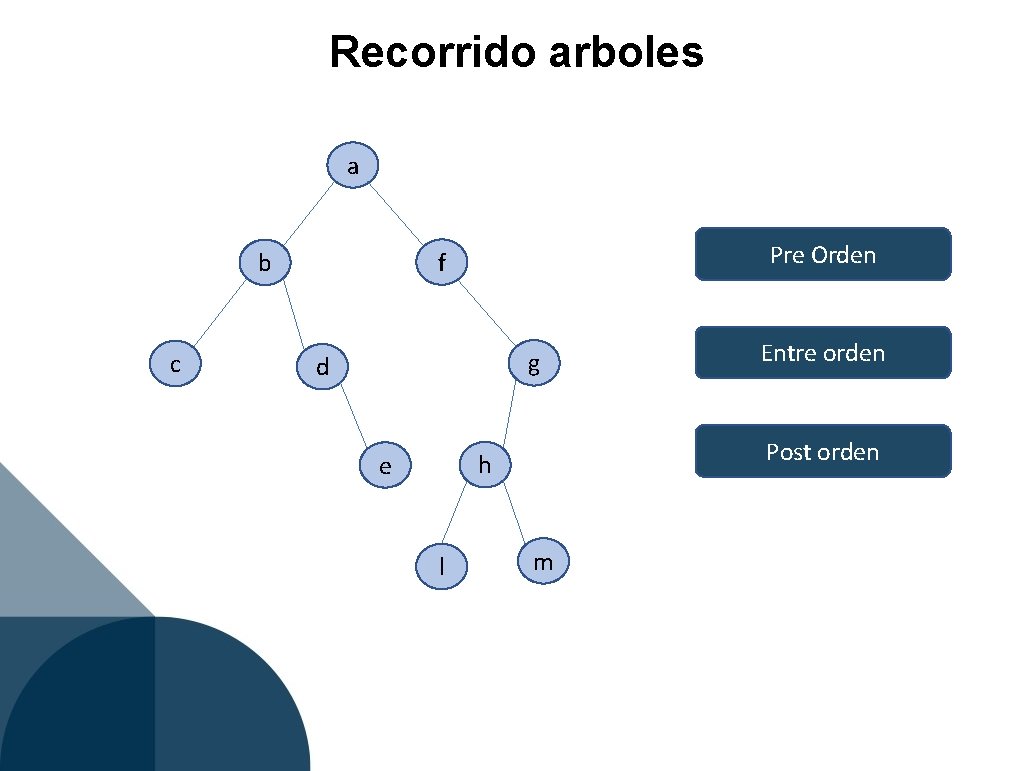
Recorrido arboles a c Pre Orden f b g d Post orden h e l Entre orden m

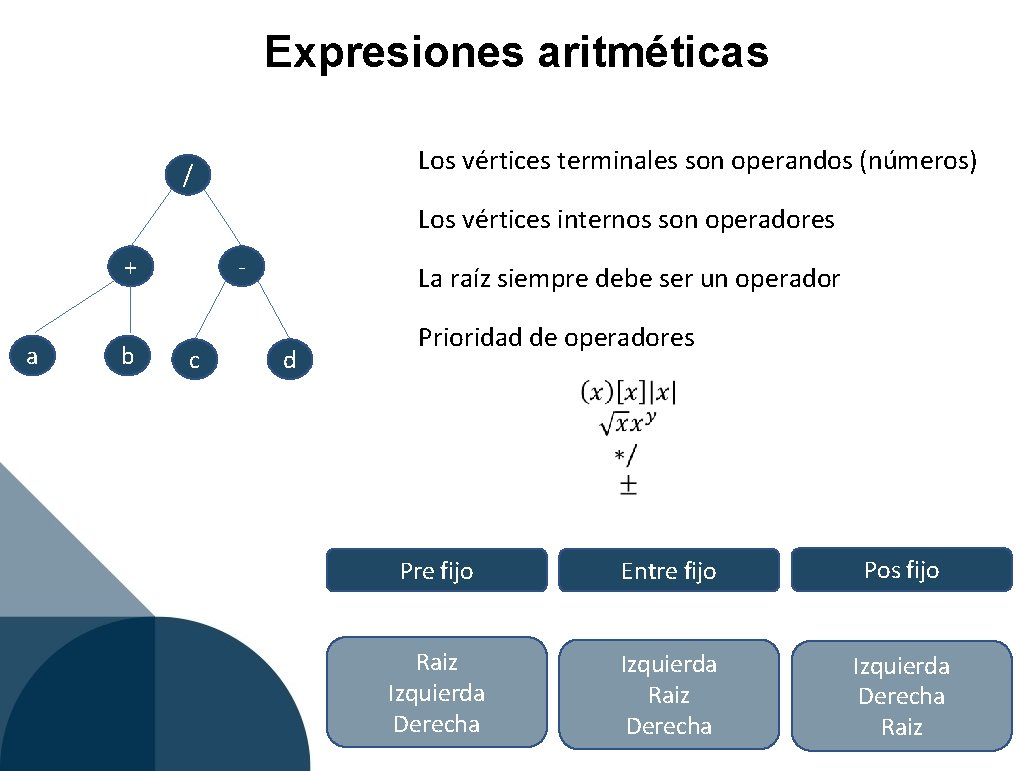
Expresiones aritméticas Los vértices terminales son operandos (números) / Los vértices internos son operadores + a b c La raíz siempre debe ser un operador d Prioridad de operadores Pre fijo Entre fijo Pos fijo Raiz Izquierda Derecha Izquierda Raiz Derecha Izquierda Derecha Raiz

PARTE 5 ALGORITMOS

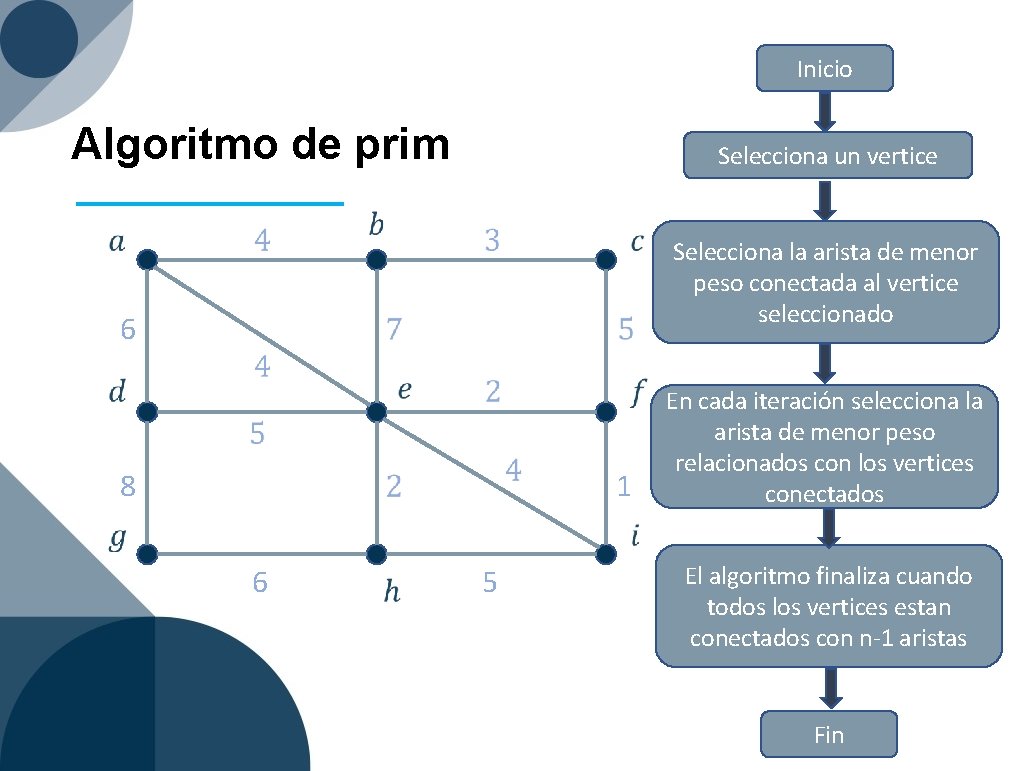
Inicio Algoritmo de prim 6 Selecciona un vertice Selecciona la arista de menor peso conectada al vertice seleccionado En cada iteración selecciona la arista de menor peso relacionados con los vertices conectados 8 1 6 5 El algoritmo finaliza cuando todos los vertices estan conectados con n-1 aristas Fin

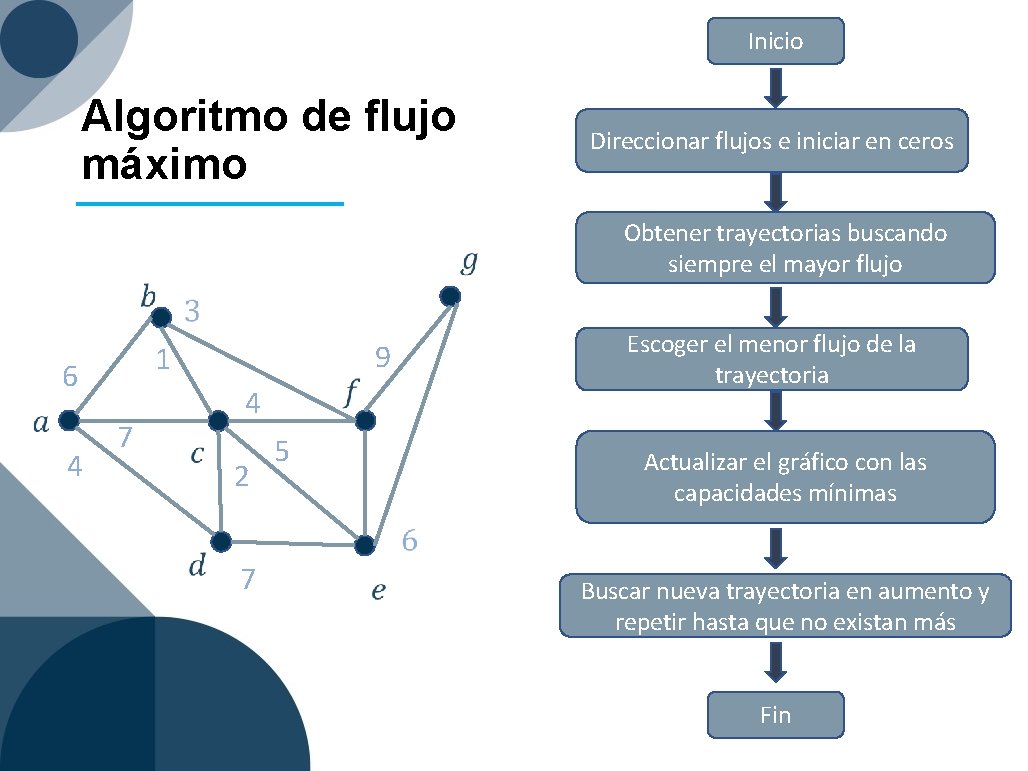
Inicio Algoritmo de flujo máximo Direccionar flujos e iniciar en ceros 4 1 6 7 Obtener trayectorias buscando siempre el mayor flujo 4 2 Escoger el menor flujo de la trayectoria 9 5 Actualizar el gráfico con las capacidades mínimas 7 Buscar nueva trayectoria en aumento y repetir hasta que no existan más Fin

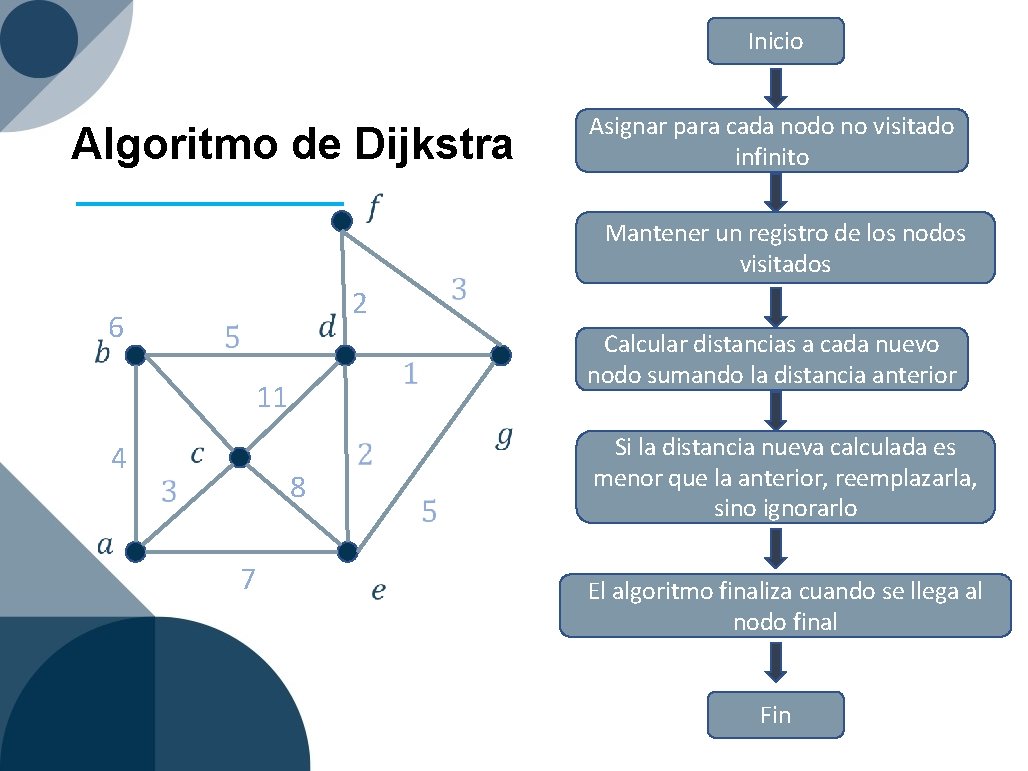
Inicio Algoritmo de Dijkstra 6 4 8 Calcular distancias a cada nuevo nodo sumando la distancia anterior 11 Mantener un registro de los nodos visitados 2 Asignar para cada nodo no visitado infinito Si la distancia nueva calculada es menor que la anterior, reemplazarla, sino ignorarlo 7 El algoritmo finaliza cuando se llega al nodo final Fin

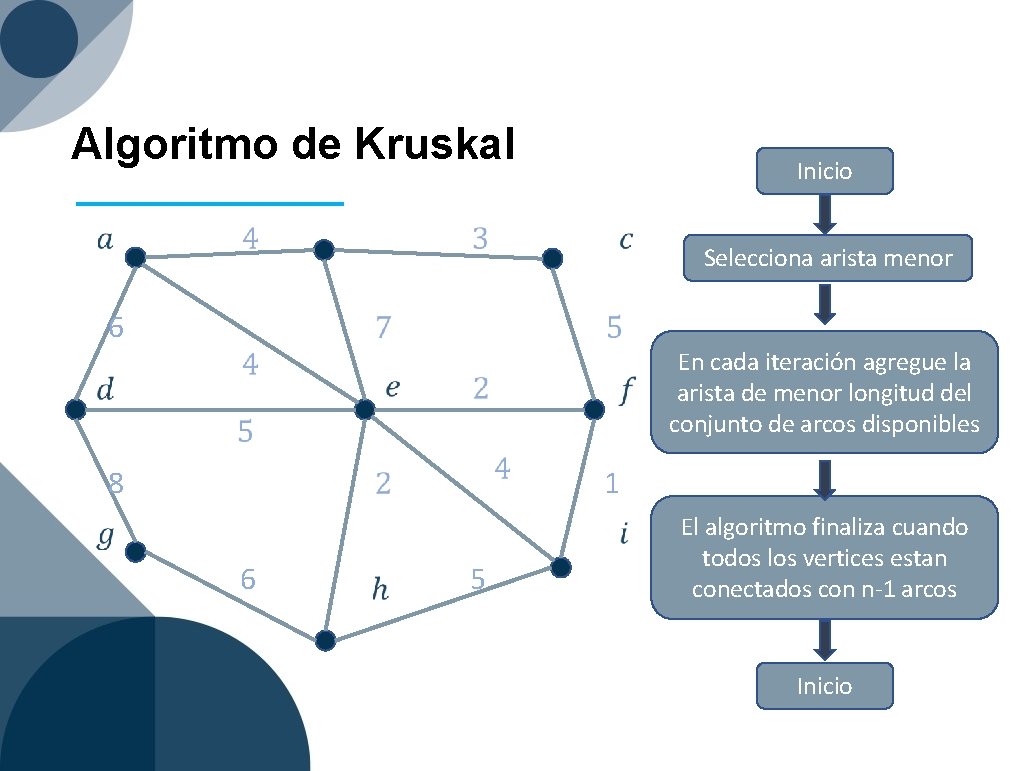
Algoritmo de Kruskal 6 Inicio 8 5 En cada iteración agregue la arista de menor longitud del conjunto de arcos disponibles 1 6 Selecciona arista menor El algoritmo finaliza cuando todos los vertices estan conectados con n-1 arcos Inicio

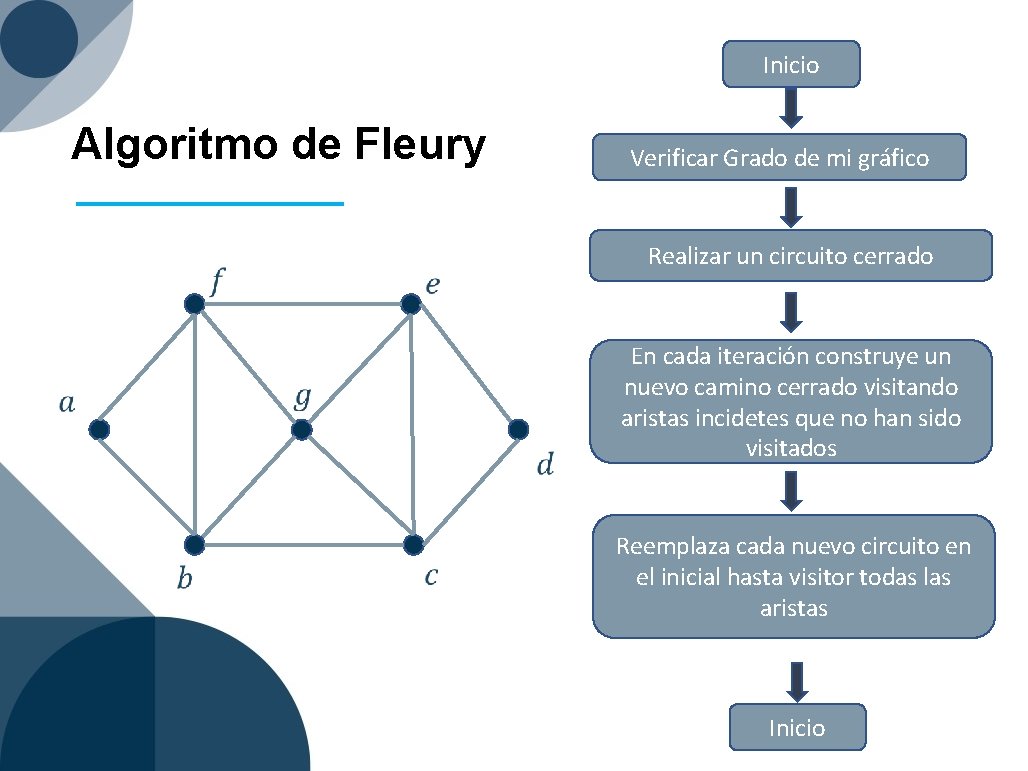
Inicio Algoritmo de Fleury Verificar Grado de mi gráfico Realizar un circuito cerrado En cada iteración construye un nuevo camino cerrado visitando aristas incidetes que no han sido visitados Reemplaza cada nuevo circuito en el inicial hasta visitor todas las aristas Inicio
 Plc semimodular
Plc semimodular Señales discretas y continuas
Señales discretas y continuas Serie de fourier exponencial
Serie de fourier exponencial Ejemplos variable aleatoria continua
Ejemplos variable aleatoria continua Recorrido posorden
Recorrido posorden Formula de la distribucion hipergeometrica
Formula de la distribucion hipergeometrica Cuantitativa discreta
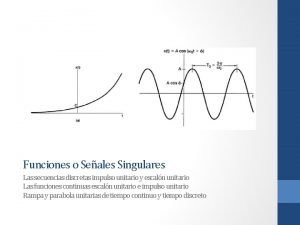
Cuantitativa discreta Derivadas de las funciones singulares
Derivadas de las funciones singulares Estructuras discretas pucp
Estructuras discretas pucp Destrezas motoras ejemplos
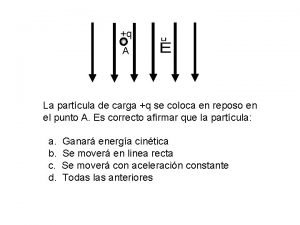
Destrezas motoras ejemplos Carga puntual
Carga puntual Ejemplos variables discretas
Ejemplos variables discretas Matemtica
Matemtica Matemtica financeira
Matemtica financeira No triangulo abc retangulo em a determine as medidas c n h
No triangulo abc retangulo em a determine as medidas c n h Ensino
Ensino Matemtica
Matemtica Matemtica financeira
Matemtica financeira Matemtica
Matemtica Matemtica financeira
Matemtica financeira Matemtica
Matemtica Exemplos de paralelogramos
Exemplos de paralelogramos Matemtica
Matemtica Matemtica
Matemtica Ensino
Ensino Quais os nomes dos polígonos
Quais os nomes dos polígonos Este parte aquele parte
Este parte aquele parte Slidetodoc.com
Slidetodoc.com A missa parte por parte
A missa parte por parte Te invitamos hacer parte
Te invitamos hacer parte Curso de grafia
Curso de grafia Curso y contenido del pensamiento
Curso y contenido del pensamiento Diploma
Diploma Linx microvix
Linx microvix Curso cid ua
Curso cid ua Eminência
Eminência Bpl oms
Bpl oms Dr alejandro guerrero
Dr alejandro guerrero Curso de evangelismo
Curso de evangelismo Correo senati
Correo senati Curso dns básico
Curso dns básico Definicio
Definicio E.p.t curso
E.p.t curso Fatfa curso auxiliar de farmacia
Fatfa curso auxiliar de farmacia Curso tecnico em agroecologia
Curso tecnico em agroecologia Ept curso
Ept curso Curso de circuito fechado de tv
Curso de circuito fechado de tv El curso favorito de los alumnos de una escuela.
El curso favorito de los alumnos de una escuela. Curso patrón de lancha deportiva de bahía
Curso patrón de lancha deportiva de bahía Desde o inicio de seu curso o jovem gerente tinha aprendido
Desde o inicio de seu curso o jovem gerente tinha aprendido Curso desenho instrucional
Curso desenho instrucional Curso de word 2007
Curso de word 2007 Curso de computacion
Curso de computacion Cumaps
Cumaps Viaje a paris fin de curso
Viaje a paris fin de curso Curso de magnetismo espiritual
Curso de magnetismo espiritual Curso mmog
Curso mmog Curso de profeta
Curso de profeta Curso variadores de frecuencia
Curso variadores de frecuencia Curso sav
Curso sav Policia antiextorsión
Policia antiextorsión Slide to doc.com
Slide to doc.com Diploma fin curso
Diploma fin curso Curso basico de project 2010
Curso basico de project 2010 Fisioterapia veterinaria curso
Fisioterapia veterinaria curso Curso intensivo de teologia do ministério ide
Curso intensivo de teologia do ministério ide Tareas del alfabetizador
Tareas del alfabetizador Curso apoyo conductual
Curso apoyo conductual Curso siltra
Curso siltra