Logica voor informatica Deel II Logica voor Informatica

Logica voor informatica Deel II Logica voor Informatica G. A. W. Vreeswijk

Berekenbaarheids-theorie Logica voor Informatica G. A. W. Vreeswijk

Het vraagstuk van berekenbaarheid n n n Zijn er inherente beperkingen aan wat computers kunnen (ongeacht programmeertaal, aantal processoren, rekentijd, en geheugen)? Zijn er problemen die, hoewel voldoende precies geformuleerd, computers principieel niet kunnen oplossen? Zo ja, welke problemen zijn dat? Logica voor Informatica G. A. W. Vreeswijk 3

Berekenbaarheids-theorie Probleem-typen Logica voor Informatica G. A. W. Vreeswijk

Vaag geformuleerde of metafysische problemen n n Hoe zou lekker bier moeten smaken? Wat is een goeie game? Wat speelt zich af in een zwart gat? Wat is de zin van het leven? Wat is gelijkheid? Logica voor Informatica Deze vraagstuk-typen zijn vaag geformuleerd, of kunnen alleen subjectief worden beantwoord of behoren tot het domein van de metafysica. “(…) wovon man nicht reden kann, darüber muß man schweigen. ” G. A. W. Vreeswijk 5

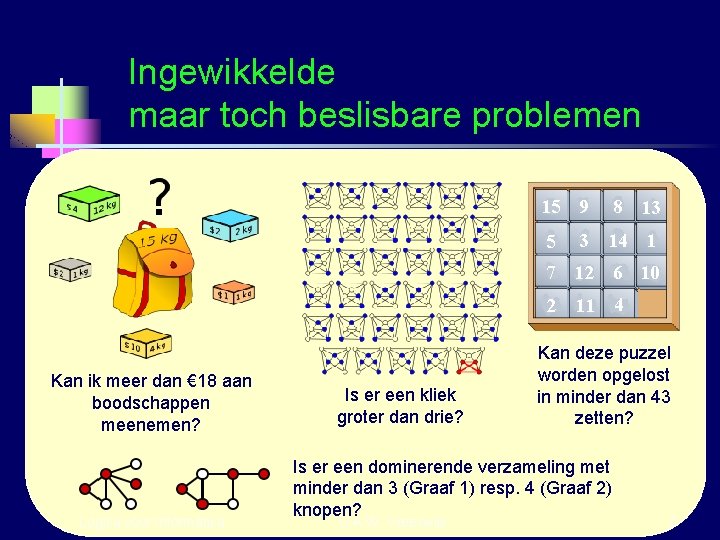
Ingewikkelde maar toch beslisbare problemen 15 9 5 8 13 3 14 1 7 12 6 10 2 11 4 Kan ik meer dan € 18 aan boodschappen meenemen? Logica voor Informatica Is er een kliek groter dan drie? Kan deze puzzel worden opgelost in minder dan 43 zetten? Is er een dominerende verzameling met minder dan 3 (Graaf 1) resp. 4 (Graaf 2) knopen? G. A. W. Vreeswijk 6

Bestaan er onbeslisbare vraagstukken? Bestaan er vraagstukken die, hoewel voldoende precies geformuleerd, computers, ongeacht programmeertaal, beschikbaar aantal processoren, rekentijd, en geheugen, principieel niet kunnen oplossen? Antwoord: JA, zulke vraagstukken bestaan. Logica voor Informatica G. A. W. Vreeswijk 7

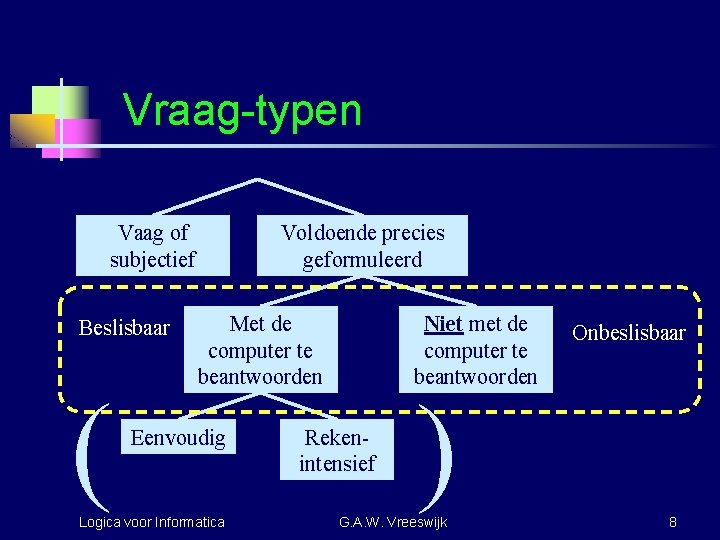
Vraag-typen Vaag of subjectief Beslisbaar ( Voldoende precies geformuleerd Met de computer te beantwoorden Eenvoudig Logica voor Informatica Niet met de computer te beantwoorden Rekenintensief Onbeslisbaar ) G. A. W. Vreeswijk 8

Onbeslisbare problemen Voorbeelden Logica voor Informatica G. A. W. Vreeswijk

Alan Turing n n 23 juni 1912: geboren in Londen 1931 -1934 kwantummechanica, al snel wiskunde aan de Universiteit van Cambridge 1935: maakt kennis met het Entscheidungsproblem 1936: On Computable Numbers, with an Application to the Entscheidungsproblem de Logical Computing Machine (later: Turing-machine) Logica voor Informatica n n n G. A. W. Vreeswijk WW 2: Government Code and Cypher School (ontcijfering Enigma) 1950: Turing test in AI 1954: overleden (cyanidevergiftiging) 10

Het stop-probleem is onbeslisbaar Stelling. Zij J een programmeertaal. Als J voldoende rijk is (en Java is dat bijvoorbeeld zeker), dan kan er geen programma h J bestaan dat voor elke programma/input-combinatie (j, i) J I kan uitmaken of j met input i stopt. n n Merk op: h/2 en j/1. Stel h bestaat, zó dat h(j, i) = 1 j(i) stopt. Logica voor Informatica G. A. W. Vreeswijk 11

Er bestaan aftelbaar veel computerprogramma’s `Bewering. Laat A een eindig alfabet zijn. De verzameling van alle eindige strings over A is aftelbaar. Bewijs: a, b, . . . , z, aa, ab, ac, …, az, ba, bb, … Gevolg: de volgende verz. zijn aftelbaar: n De verz. van alle programma’s in de taal J. Logica voor Informatica n n De verz. van alle computerprogramma’s in bestaande programmeertalen De verz. van alle mogelijke computerprogramma’s in alle mogelijke (dus ook toekomstige) programmeertalen. G. A. W. Vreeswijk 12

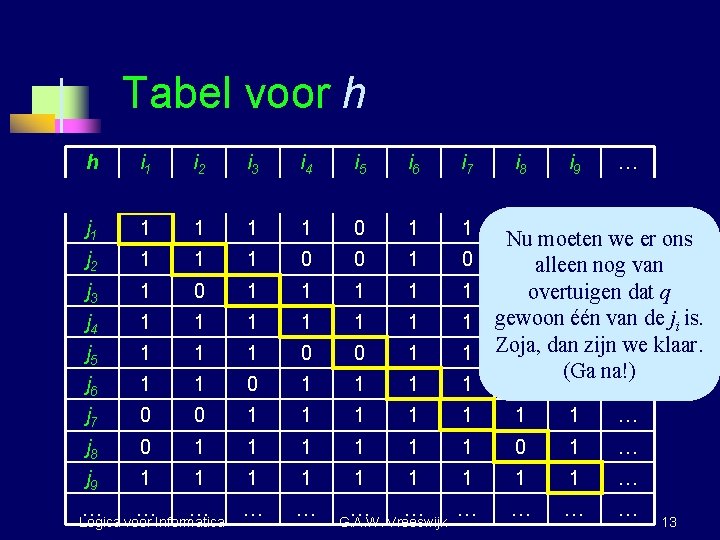
Tabel voor h h i 1 i 2 i 3 i 4 i 5 i 6 i 7 i 8 i 9 … q 0 0 1 0 … j 1 1 1 0 1 1 j 2 1 1 1 0 0 1 0 j 3 1 0 1 1 1 j 4 1 1 1 1 j 5 1 1 1 0 0 1 1 j 6 1 1 0 1 1 j 7 0 0 1 1 j 8 0 1 1 j 9 1 1 … … … Logica voor Informatica 0 1 … Nu moeten we er ons 1 alleen 0 nog…van 1 overtuigen 1 … dat q gewoon 1 1één van … de ji is. Zoja, we klaar. 0 dan 1 zijn … (Ga na!) 1 1 … 1 1 0 1 … 1 1 1 … … … … G. A. W. Vreeswijk 13

Het stop-probleem is onbeslisbaar n n n Halting programma, h, is zó, dat h(j, i) = 1 j(i) stopt. Omgekeerd: h(j, i) = 0 j(i) stopt niet. diagonalisatie Bekijk programma q/1: q(i): als h(i, i) = 0 stop, anders draai oneindige loop. Stopt q(q) ? ü Volgens q’s definitie: q(q) stopt h(q, q) = 0. ü Volgens h’s definitie: q(q) stopt h(q, q) = 1. Tegenspraak. Logica voor Informatica G. A. W. Vreeswijk 14

Het stop-probleem voor eindige collecties Is het stop-probleem onbeslisbaar voor eindige collecties van programma’s? n Piet: “Nog steeds niet. Het diagonalisatieargument is nog steeds van kracht (op de nu eindige h-matrix). ” n Truus: “Ja. Er bestaat een controle-programma h dat een 1 afdrukt d. e. s. d. a. j stopt met input i. ” “Zonder overigens te weten hoe h er uit ziet. ” Logica voor Informatica G. A. W. Vreeswijk 15

Carcassonne Logica voor Informatica Youtube gameplay instruction G. A. W. Vreeswijk 16

Logica voor Informatica G. A. W. Vreeswijk 17

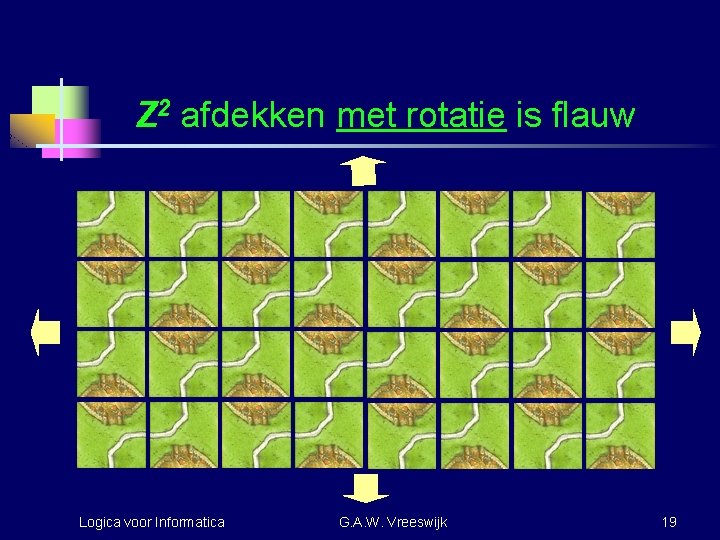
Voorbeeld van een Carcassonne tegelset Stel: van elke tegel zijn oneindig veel exemplaren voorradig Logica voor Informatica Is het mogelijk het platte vlak met deze tegelset af te dekken, zonder tegels te roteren? G. A. W. Vreeswijk 18

Z 2 afdekken met rotatie is flauw Logica voor Informatica G. A. W. Vreeswijk 19

Afdekken zonder rotatie Voorbeelden waarin rotatie niet is toegestaan: n Noord-Zuid oriëntatie. n Schaduwen. Logica voor Informatica G. A. W. Vreeswijk 20

Wang (1961) n n Vermoeden: “er bestaat een algoritme (rekenrecept) dat voor alle tegelsets kan beslissen of deze het platte vlak kunnen vullen” Idee: probeer steeds grotere gebieden te bedekken, totdat: ü ü een gebied niet bedekt kan worden (mislukking) een periodiek patroon ontstaat (succes) Logica voor Informatica G. A. W. Vreeswijk 21

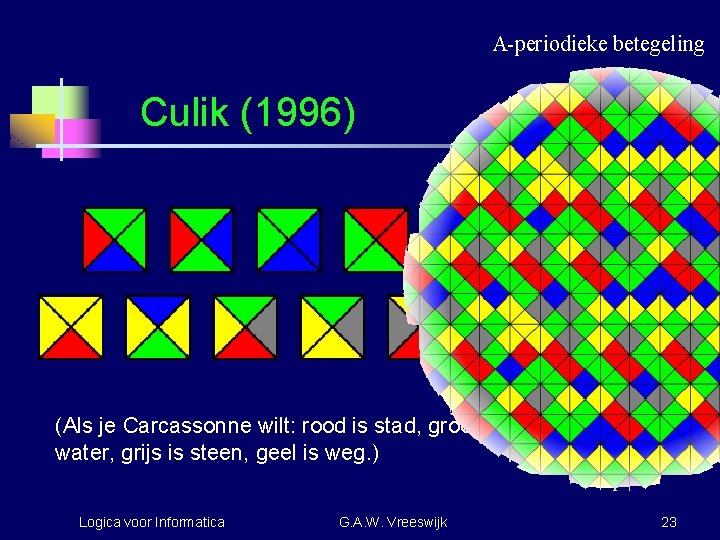
Het tegel-probleem van Wang n n n 1961: Hoa Wang: "Proving theorems by pattern recognition—II", Bell System Tech. Journal 40(1): 1– 41. Algoritme nam periodiciteit aan. 1966: Robert Berger: "The undecidability of the domino problem", Memoirs Amer. Math. Soc. 66(1966). A-periodieke set bevatte 20, 426 tegels. 1996: Karel Culik: "An aperiodic set of 13 Wang tiles", Discrete Mathematics 160, 245– 251. Logica voor Informatica G. A. W. Vreeswijk 22

A-periodieke betegeling Culik (1996) (Als je Carcassonne wilt: rood is stad, groen is land, blauw is water, grijs is steen, geel is weg. ) Logica voor Informatica G. A. W. Vreeswijk 23

A-periodic texture mapping Voorbeelden waarin rotatie niet is toegestaan: n Noord-Zuid oriëntatie n Schaduwen op terrein-tegels. n n n Logica voor Informatica Jos Stam (1997), Aperiodic Texture Mapping Michael F. Cohen, Jonathan Shade, Stefan Hiller, Oliver Deussen (2003), Wang Tiles for Image and Texture Generation Li-Yi Wei (2004), Tile-Based Texture Mapping on Graphics Hardware G. A. W. Vreeswijk 24

Li-Yi Wei (2004), afbeeldingen Chelsea Robertson (2005) Logica voor Informatica G. A. W. Vreeswijk 25

Er bestaat geen algoritme! Er bestaat geen algoritme, er kan ook geen algoritme bestaan, en er zal ook nooit een algoritme komen, dat voor alle niet-roteerbare Carcassonne-tegelsets kan bepalen of deze het platte vlak kunnen betegelen. n n Het bewijs komt er op neer elk specifiek zg. haltingprobleem te vertalen naar een specifiek betegelingsprobleem. . en het universele halting-probleem is onbeslisbaar. Logica voor Informatica G. A. W. Vreeswijk 26

Emil L. Post n n n 1897: geboren in Augustow, emigratie naar VS 1909: verlies van linkerarm 1920: doctoraalscriptie over Principia Mathematica 1921: ontdekking onvolledigheidsstelling Gödel, eerste aanval van bipolar, demotie carrière 1936: Post-machine Logica voor Informatica n n G. A. W. Vreeswijk 1944: opsombaarheid, Turing-degree 1954: overleden (hartaanval) 27

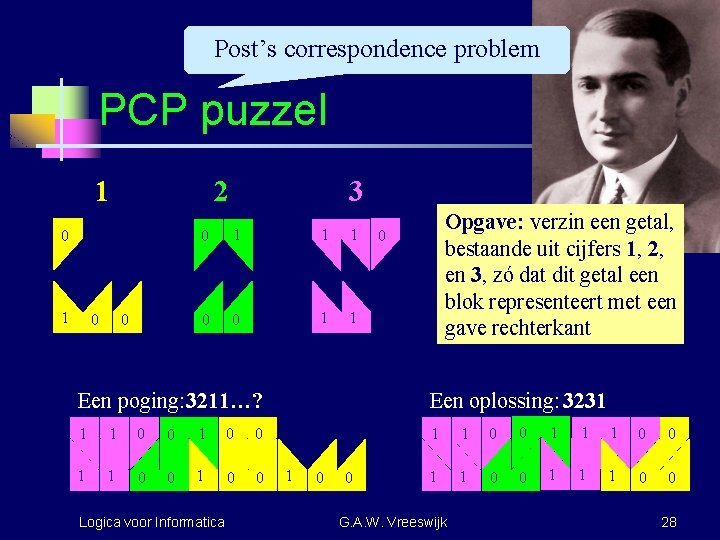
Post’s correspondence problem PCP puzzel 1 2 0 1 0 0 3 0 1 1 1 0 0 1 1 Opgave: verzin een getal, bestaande uit cijfers 1, 2, en 3, zó dat dit getal een blok representeert met een gave rechterkant 0 Een poging: 3211…? Een oplossing: 3231 1 1 0 0 1 1 0 0 1 1 1 0 0 Logica voor Informatica 1 0 0 G. A. W. Vreeswijk 28

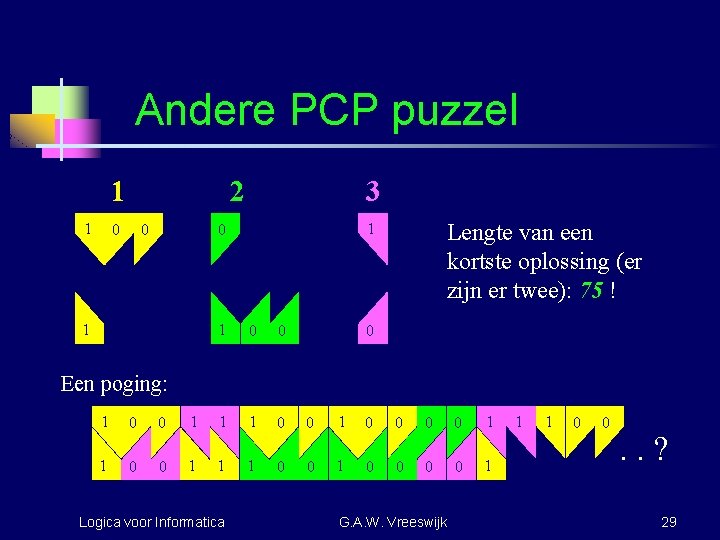
Andere PCP puzzel 1 1 2 0 0 3 1 Lengte van een kortste oplossing (er zijn er twee): 75 ! 1 0 0 0 0 Een poging: 1 1 0 0 0 1 1 1 Logica voor Informatica 0 0 1 0 0 0 G. A. W. Vreeswijk 0 1 1 1 0 0 . . ? 29

Tijdbalk voor onbeslisbaarheid n n n n 1889: Peano: formeel systeem voor rekenkunde 1900: Hilbert: 23 problemen voor de 20 e eeuw 1910 -1913: Whityehead & Russell: principia methematica 1920: Hilbert's programma 1928: het Entscheidungsproblem 1936: lambda-calculus → eerste onbeslisbare probleem 1936: Turing machine 1936: Post machine Logica voor Informatica G. A. W. Vreeswijk 30

Berekenbaarheids-theorie Definities en resultaten Logica voor Informatica G. A. W. Vreeswijk

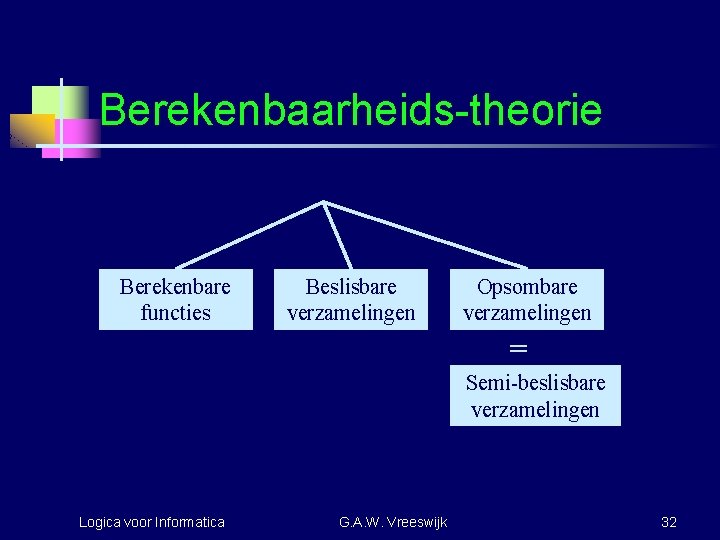
Berekenbaarheids-theorie Berekenbare functies Beslisbare verzamelingen Opsombare verzamelingen = Semi-beslisbare verzamelingen Logica voor Informatica G. A. W. Vreeswijk 32

Berekenbaar, opsombaar, beslisbaar n n n Een functie f : N N heet berekenbaar als er een programma te schrijven valt die deze functie kan uitrekenen. Een verzameling A N heet opsombaar als er een programma te schrijven valt die precies deze verzameling kan afdrukken. Een verzameling A N heet beslisbaar als er een programma te schrijven valt die kan uitmaken of een getal in A zit. Logica voor Informatica G. A. W. Vreeswijk 33

Berekenbaarheids-theorie Berekenbare functies Logica voor Informatica G. A. W. Vreeswijk

Berekenbaarheid Maakt het nog uit in welke programmeertaal? Een partiële functie f : N N heet berekenbaar als er een computer-programma π/1 te schrijven is die f kan uitrekenen. Eenvoudig voorbeeld: n f : N → N beeldt x af op √x mits √x geheel is; anders ongedefinieerd. n Is deze functie berekenbaar? n Verzin andere functies N → N. Berekenbaar? Logica voor Informatica G. A. W. Vreeswijk 35

Berekenbaarheid preciezer definiëren Zij f : N N een partiële functie en J een programmeertaal. We zeggen dat programma π J de functie f berekent als voor elke n N en elke uitvoering van π(n) het volgende geldt: n Als f↓n, wordt f(n) afgedrukt. n Als f↑n, wordt niets afgedrukt. Logica voor Informatica Berekenbaarheid. Een partiële functie f : N N heet berekenbaar, ook wel: effectief berekenbaar, als er een programma π/1 J bestaat welke f berekent. G. A. W. Vreeswijk 36

Aanvullingen op berekenbaarheids-definitie n Als π een uitkomst afdrukt, dan is π eigenlijk klaar, en mag het stoppen. Als π niet op deze manier werkt, kunnen we π veranderen in een programma π’ dat altijd stopt na het afdrukken van een resultaat. Logica voor Informatica n n Als f↓n kan het op zich nog best lang duren voordat π de uitkomst f(n) afdrukt. Als π niets afdrukt, kan dat twee redenen hebben. 1. 2. Het kan zijn dat π heeft “ontdekt” dat f↑n en daarom stopt (of doorgaat zonder ooit nog wat af te drukken). Het kan zijn dat f↓n en π nog bezig is f(n) uit te rekenen. G. A. W. Vreeswijk 37

Er bestaan hoogstens aftelbaar oneindig veel berekenbare functies Eigenlijk wordt elke berekenbare functie berekend door aftelbaar oneindig veel programma’s. Dit heet het Padding Lemma. Bewijs: n Kies een voldoende krachtige programmeertaal, bijvoorbeeld J. n Alle berekenbare functies B NN worden berekend door tenminste één element uit J. n We hebben zojuist een injectie B → J geconstrueerd. n Eerdere stelling uit dictaat: als f: X → Y een injectie is, dan is |X| ≤ |Y|. Dus |B| ≤ |J|. Logica voor Informatica G. A. W. Vreeswijk 38

Het padding lemma. . . y : =4; while ( y < x ) {. . . } x : = y − z; . . . Logica voor Informatica . . . y : =4; while ( y < x ) {. . . } z : = z; /* bla */ x : = y − z; . . . G. A. W. Vreeswijk 39

Er bestaan onberekenbare functies Volgt uit: Stelling. De verzameling NN bevat tenminste één onberekenbare functie. Bewijs: n n Er zijn overaftelbaar veel functies van N naar N (i. e. , NN is overaftelbaar). Maar er zijn hoogstens aftelbaar veel berekenbare functies van N naar N. (Zojuist gezien!) Logica voor Informatica G. A. W. Vreeswijk 40

Het leeuwendeel van N N is onberekenbaar Volgt uit: Stelling. De verzameling NN bevat overaftelbaar veel onberekenbare functies. Bewijs: n n n NN bevat aftelbaar veel berekenbare functies B. Het complement NN ─ B (de verz. van onberekenbare functies) kan niet aftelbaar zijn. Dus is het complement overaftelbaar. Logica voor Informatica G. A. W. Vreeswijk 41

Vragen Welke van de volgende functies N → N is berekenbaar? n De identiteitsfunctie. n De compositie (samenstelling) van twee berekenbare functies. n De inverse van een berekenbare functie, vooropgesteld dat de inverse bestaat. Dit is een moeilijke… we hebben hier een techniek voor nodig, genaamd “zwaluwstaarten”. Logica voor Informatica G. A. W. Vreeswijk 42

“Zwaluwstaarten” (“dovetailing”) Laat programma π/1 een functie f : N → N uitrekenen. π kan quasi-parallel worden uitgevoerd op N: n n 1. 2. 3. 4. 5. Eén stap π(0), één stap π(1), één stap π(2). Eén stap π(0), één stap π(1) , één stap π(2), één stap π(3). … Logica voor Informatica G. A. W. Vreeswijk 43

De inverse van een injectieve berekenbare functie (1) bestaat, en (2) is berekenbaar Bewijs: Laat π/1 de injectie f : X → Y uitrekenen. 1. De inverse, g (als part. fun. ), bestaat. 2. Algoritme om g(n) te berekenen: ü ü Voer π quasi-parallel op N uit. Als g(n) gedefinieerd is, zal f(g(n)) = n en zal π voor zekere m ooit n afdrukken. In dat geval geldt m = g(n)―stop. Logica voor Informatica G. A. W. Vreeswijk link naar pin code analyse 44

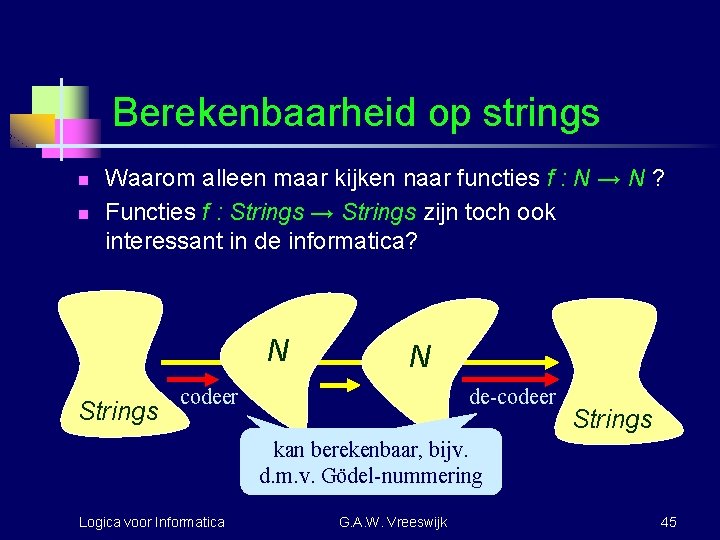
Berekenbaarheid op strings n n Waarom alleen maar kijken naar functies f : N → N ? Functies f : Strings → Strings zijn toch ook interessant in de informatica? N Strings N codeer de-codeer Strings kan berekenbaar, bijv. d. m. v. Gödel-nummering Logica voor Informatica G. A. W. Vreeswijk 45

Gödel nummering n n n ASCII: 0 -127 codeert letters, cijfers, en leestekens Het woord “abces”: 97, 98, 99, 101, 115 Naar uniek natuurlijk getal: 297398599710111115 Deze injectie Strings → N is berekenbaar Omgekeerd is injectieve (partiële!) functie N → Strings ook berekenbaar Partieel, want welke string zou vertegenwoordigd worden door 29973898 ? Logica voor Informatica G. A. W. Vreeswijk 46

Berekenbaarheid op andere verzamelingen n n Op Stringsn → Strings. Op Strings* → Strings. (Waarbij Strings* = Strings 0 Strings 1 Strings 2 . . . Voorbeeld: aap#noot#mies ↔ (aap, noot, mies). Op Strings* → Strings*. Op Plaatjes* → Plaatjes* , Audio, Video, … Alle berekeningen moeten wel “batch” zijn. ü ü ü Geen interactiviteit. Geen asynchroniciteit. Geen “orakel”van buiten (software-updates). Logica voor Informatica G. A. W. Vreeswijk 47

Berekenbaarheids-theorie Beslisbaarheid Logica voor Informatica G. A. W. Vreeswijk

Beslisbaarheid preciezer definiëren We zeggen dat programma π/1 J beslist over verzameling X N als π voor elk getal n N kan uitmaken of n X. n n n We zeggen dat X N beslisbaar is, als er een programma bestaat dat over X kan beslissen. “kan uitmaken of” → druk 1 af als n X, druk anders 0 af. Elke eindige verzameling is beslisbaar. Als X en Y beslisbaar zijn, dan zijn hun vereniging, doorsnede, verschil en complement dat ook. (Ga na!) Logica voor Informatica G. A. W. Vreeswijk 49

Een model-bewijs Te bewijzen: als X en Y beslisbaar zijn, dan is X Y het ook. Bewijs: n Laat j 1 en j 2 programma’s zijn die over X resp. Y kunnen beslissen. n Het is nu in principe mogelijk een programma j te schrijven die over X Y beslist, als volgt: ü Zij n N willekeurig. ü ü Laat j de waarden j 1(n) en j 2(n) uitrekenen door j 1 en j 2 aan te roepen. Laat j de waarde 1 teruggeven als en slechts als j 1(n)=1 of j 2(n)=1 (en 0 anders). Logica voor Informatica G. A. W. Vreeswijk 50

Beslisbaarheid van de propositielogica n Is de (verz. van tautologieën in de) propositielogica beslisbaar? I. e. , bestaat er een algoritme waarmee bepaald kan worden of een formule een tautologie is? Ja! : ü ü n Waarheidstabellen Semantische tableaus Vragen: ü ü Kan men m. b. v. het Hilbert-bewijssysteem beslissen of een formule een tautologie is? M. b. v. het Fitch-bewijssysteem (natuurlijke deductie)? Logica voor Informatica G. A. W. Vreeswijk 51

(Geldigheid in) predikatenlogica is semi-beslisbaar Semi-beslisbaarheid We zeggen dat programma π/1 semi-beslist over X N, als π voor n X kan uitmaken of n X. n n n We zeggen dat X N semibeslisbaar is, als er een programma π bestaat dat semi-beslist over X. “kan uitmaken of” → druk 1 af als n X, druk anders 0 af Als n X dan zal π een 0 afdrukken, of oneindig doorlopen. Zwakte: het heeft geen zin om op π te wachten. Logica voor Informatica G. A. W. Vreeswijk 52

Berekenbaarheids-theorie Opsombaarheid Logica voor Informatica G. A. W. Vreeswijk

Opsombaarheid preciezer definiëren We zeggen dat programma π/0 J de verzameling X N opsomt als π precies alle getallen uit X kan afdrukken. n n We zeggen dat X N opsombaar is, als er een programma bestaat dat X kan opsommen. π heeft geen input nodig. π is niet gebonden aan een volgorde. π mag elementen herhaald afdrukken. Er kunnen onvoorspelbare en willekeurige lange pauzes voorkomen tussen het afdrukken van getallen. Logica voor Informatica G. A. W. Vreeswijk 54

Raadsel: is Nx. N opsombaar? 31 30 29 28 27 26 13 12 11 10 25 14 3 2 9 24 15 4 1 8 23 16 5 6 7 22 17 18 19 20 21 Logica voor Informatica G. A. W. Vreeswijk • Is suggestieve aftelling. • Kun je ook een algoritme bedenken dat elementen in het platte vlak aftelt? • I. e. , kun je een opsomming bedenken? 55

Een mogelijke opsomming van Nx. N n n n: =1 while 1 { ü ü ontbind n in priemfactoren als n geen andere priemdelers heeft dan 2 en 3, print dan de exponenten als geordend paar, bv. 27384 → (7, 84) (Print niks in het andere geval. ) } Logica voor Informatica G. A. W. Vreeswijk 56

Men kan bewijzen: P( X N is opsombaar ) = 0 Opsombaar ≠ aftelbaar Stelling. Er bestaan aftelbare verzamelingen die niet opsombaar zijn. Bewijs: Gevolg: n Er bestaan tenminste NN n Overaftelbaar veel verschillende aftelbare verzamelingen bezitten geen n Er bestaan “maar” aftelbaar veel opsomming! opsombare verzamelingen. Logica voor Informatica G. A. W. Vreeswijk 57

Semi-beslisbaar = opsombaar n Stel X is opsombaar. Laat π/0 de verz. X opsommen. Semi-beslisprocedure: ü n Draai π. Als n X dan zal n uiteindelijk verschijnen; druk in dat geval 1 af. Stel X is semi-beslisbaar. Laat π/1 semi-beslissen over X. Opsom-algoritme: zwaluwstaart-methode ü ü Voer π/0 semi-parallel uit op N. Voor elke n X zal π vroeg of laat een 1 afdrukken. Druk deze n af. Als (eventueel!) een 0 wordt afgedrukt, druk dan niets af. Logica voor Informatica G. A. W. Vreeswijk 58

Vragen over opsombaarheid n n Is elke eindige verzameling X N opsombaar? Stel, X en Y zijn opsombaar. ü ü ü Ja. Is X Y opsombaar? Is X ─ Y opsombaar? Is XC = N ─ X opsombaar? Logica voor Informatica G. A. W. Vreeswijk ü ü ü Ja. Ja. Weet niet. 59

Complementair opsombaar N Logica voor Informatica G. A. W. Vreeswijk 60

Complementair opsombaar Een verzameling X N heet complementair opsombaar als het complement opsombaar is. n n n Co-opsombaar, co-enumereerbaar, co-recursief enumereerbaar, corecursively enumerable, co-r. e. Stelling van Post: X N is beslisbaar X is opsombaar en complementair opsombaar. Antwoord op eerdere vraag: niet alle complementen van opsombare verz. zijn dus opsombaar. (Immers: niet alle verz. zijn beslisbaar. ) Logica voor Informatica G. A. W. Vreeswijk 61