Relaciones de Equivalencia y Relaciones de Orden Mag

Relaciones de Equivalencia y Relaciones de Orden Mag. Miguel Sierra Curso: Estructuras Discretas PUCP

Relaciones de Equivalencia Una relación R en A, es una relación de equivalencia, si R es reflexiva, simétrica y transitiva (RST). Se define clase de equivalencia del elemento a, como: [a] = {x A / x R a} [a] = {Los vértices desde donde se llega a a, en un solo paso} El conjunto de todas las clases de equivalencia de A, es el conjunto A/R, denominado el conjunto cociente: A/R = {[a] / a A } Ejm. : A={0, 1, 2, 3, 4, 5, 6} R={(x, y) A*A / (x-y) es divisible por 3} R= {(0, 0), (0, 3), (0, 6), (1, 1), (1, 4), (2, 2), (2, 5), (3, 0), (3, 3), (3, 6), (4, 1), (4, 4), (5, 2), (5, 5), (6, 0), (6, 3), (6, 6)}

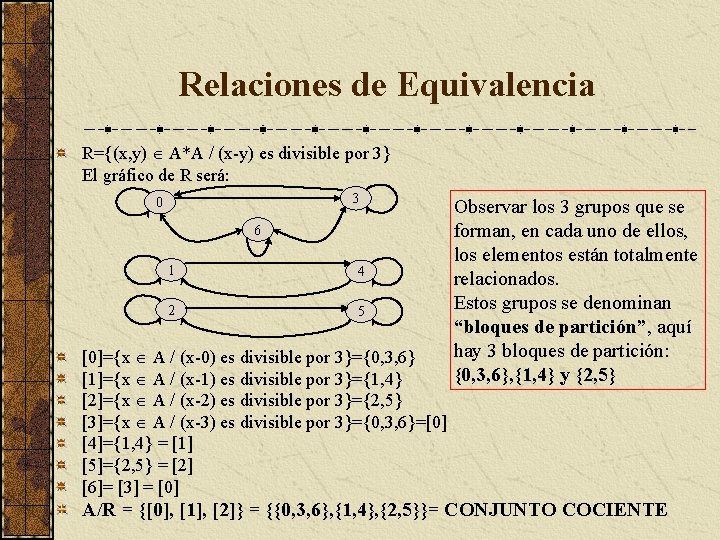
Relaciones de Equivalencia R={(x, y) A*A / (x-y) es divisible por 3} El gráfico de R será: 3 0 6 1 4 2 5 [0]={x A / (x-0) es divisible por 3}={0, 3, 6} [1]={x A / (x-1) es divisible por 3}={1, 4} [2]={x A / (x-2) es divisible por 3}={2, 5} [3]={x A / (x-3) es divisible por 3}={0, 3, 6}=[0] [4]={1, 4} = [1] [5]={2, 5} = [2] [6]= [3] = [0] Observar los 3 grupos que se forman, en cada uno de ellos, los elementos están totalmente relacionados. Estos grupos se denominan “bloques de partición”, aquí hay 3 bloques de partición: {0, 3, 6}, {1, 4} y {2, 5} A/R = {[0], [1], [2]} = {{0, 3, 6}, {1, 4}, {2, 5}}= CONJUNTO COCIENTE

Relaciones de Equivalencia Teorema: Sea R una relación de equivalencia en A, con a, b A, entonces: [a] = [b] ↔ a R b [a] ≠ [b] ↔ [a] [b] = Ø Partición: Una partición de un conjunto no vacío A, es una colección P= {A 1, A 2, . . An}, de subconjuntos no vacíos de A, tales que: Ai Aj = Ø , si i ≠ j A 1 A 2 … An = A Los subconjuntos Ai, son llamados bloques de partición. Teorema: Concordancia entre Relaciones de equivalencia y Particiones Dada una relación de equivalencia R en A, entonces, el conjunto cociente A/R es una partición de A. Dada una partición P de A, entonces se puede formar una relación de equivalencia R, definida por: x R y ↔ Ai P, tal que: x Ai y Ai

Relaciones de Orden Una relación R en A, es de orden parcial, si R es reflexiva, antisimétrica y transitiva (RAT). Se dice entonces que, el conjunto A es un conjunto parcialmente ordenado, y se denota por: (A, R) ó (A, ≤) ó A (Observar que ≤ es lo mismo que R) R-1 también es un orden parcial llamado el dual del orden parcial R Si a y b son elementos de (A, ≤), se dice que: a<b si (a ≤ b y a ≠ b) a y b son comparables si: a≤bó b≤a Si cada par de elementos de A son comparables, entonces, A es un conjunto totalmente ordenado.

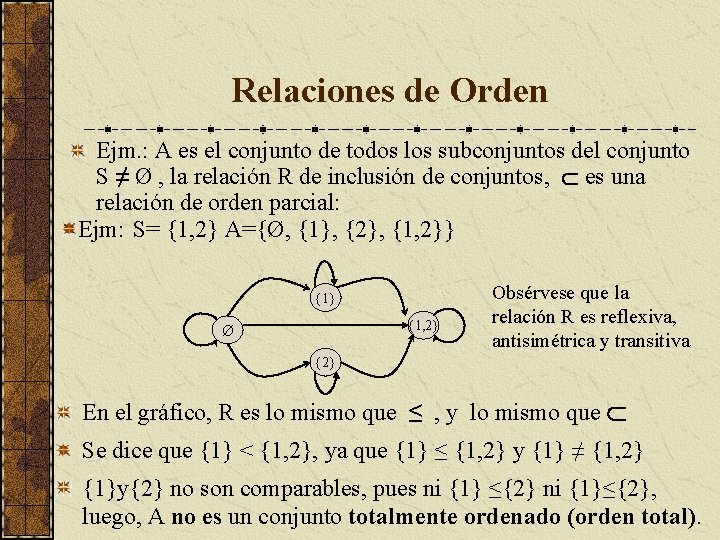
Relaciones de Orden Ejm. : A es el conjunto de todos los subconjuntos del conjunto S ≠ Ø , la relación R de inclusión de conjuntos, es una relación de orden parcial: Ejm: S= {1, 2} A={Ø, {1}, {2}, {1, 2}} {1, 2} Ø Obsérvese que la relación R es reflexiva, antisimétrica y transitiva {2} En el gráfico, R es lo mismo que ≤ , y lo mismo que Se dice que {1} < {1, 2}, ya que {1} ≤ {1, 2} y {1} ≠ {1, 2} {1}y{2} no son comparables, pues ni {1} ≤{2} ni {1}≤{2}, luego, A no es un conjunto totalmente ordenado (orden total).

Relaciones de Orden Ejm. : Sea A= Z+ , y sea R la relación ≤ : a ≤ b ↔ (b-a) es un número natural Obsérvese que cualquier par de números a y b, cumplen, o bien a ≤ b o bien b ≤ a Luego cada par de números a y b son comparables, por lo tanto, esta relación es un orden total, o A es un conjunto totalmente ordenado. La relación de divisibilidad R, definida por: a R b ↔ a | b ↔ a es divisor de b R si es una relación de orden (reflexiva antisimetrica y transitiva). Es una relación de orden parcial. R no es un orden total, ya que no todas las parejas de números son comparables, por ejemplo, 3 y 4 no son comparables, ya que no cumplen ni 3 | 4 , ni 4 | 3 El dual de R (es divisor de), R-1 (es múltiplo de) también es un orden parcial

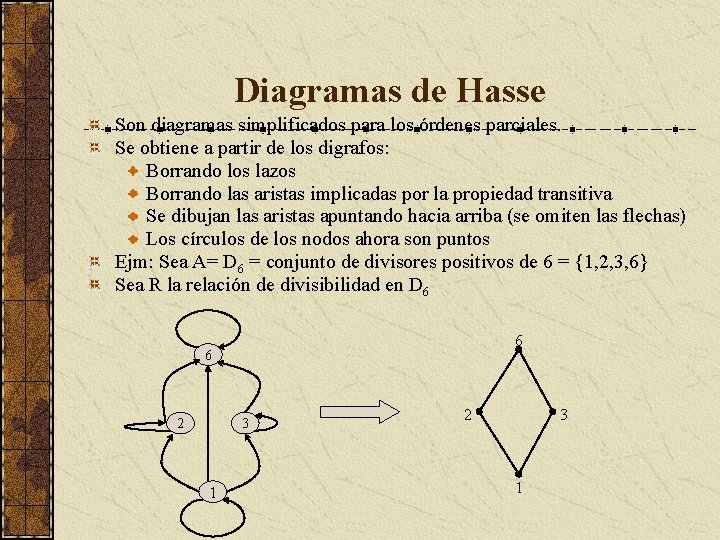
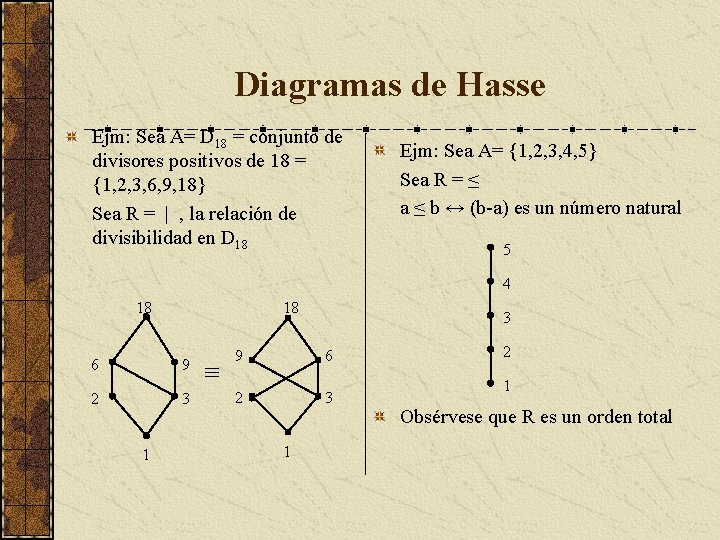
Diagramas de Hasse Son diagramas simplificados para los órdenes parciales. Se obtiene a partir de los digrafos: Borrando los lazos Borrando las aristas implicadas por la propiedad transitiva Se dibujan las aristas apuntando hacia arriba (se omiten las flechas) Los círculos de los nodos ahora son puntos Ejm: Sea A= D 6 = conjunto de divisores positivos de 6 = {1, 2, 3, 6} Sea R la relación de divisibilidad en D 6 6 6 2 3 1

Diagramas de Hasse Ejm: Sea A= D 18 = conjunto de divisores positivos de 18 = {1, 2, 3, 6, 9, 18} Sea R = | , la relación de divisibilidad en D 18 Ejm: Sea A= {1, 2, 3, 4, 5} Sea R = ≤ a ≤ b ↔ (b-a) es un número natural 5 4 18 18 6 9 2 3 1 ≡ 3 9 6 2 3 1 2 1 Obsérvese que R es un orden total

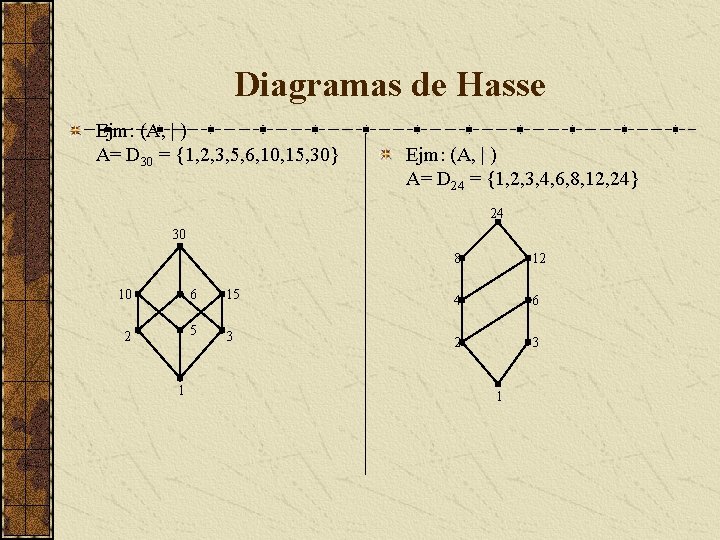
Diagramas de Hasse Ejm: (A, | ) A= D 30 = {1, 2, 3, 5, 6, 10, 15, 30} Ejm: (A, | ) A= D 24 = {1, 2, 3, 4, 6, 8, 12, 24} 24 30 8 12 10 6 15 4 6 2 5 3 2 3 1 1

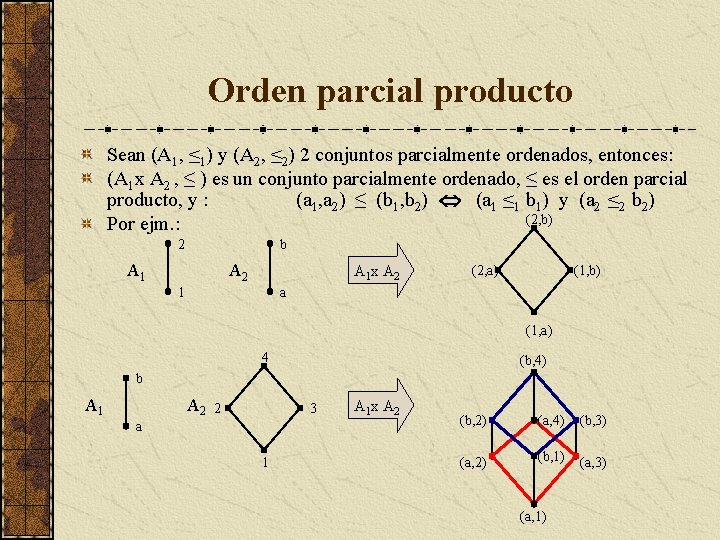
Orden parcial producto Sean (A 1, ≤ 1) y (A 2, ≤ 2) 2 conjuntos parcialmente ordenados, entonces: (A 1 x A 2 , ≤ ) es un conjunto parcialmente ordenado, ≤ es el orden parcial producto, y : (a 1, a 2) ≤ (b 1, b 2) (a 1 ≤ 1 b 1) y (a 2 ≤ 2 b 2) (2, b) Por ejm. : 2 b A 1 A 2 A 1 x A 2 1 (2, a) (1, b) a (1, a) 4 (b, 4) b A 1 A 2 2 3 a 1 A 1 x A 2 (b, 2) (a, 4) (b, 3) (a, 2) (b, 1) (a, 3) (a, 1)

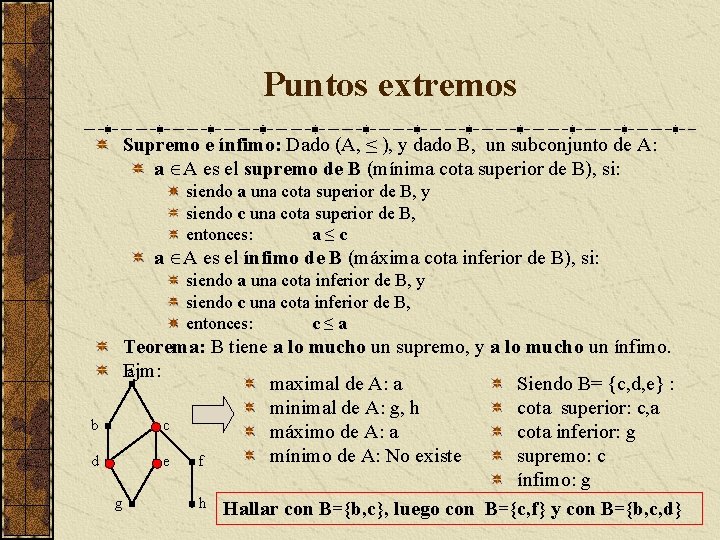
Puntos extremos Sea (A, ≤ ) un conjunto parcialmente ordenado: Maximal y minimal de A: a A es un elemento maximal de A, si no hay c A / a < c {No existe un c A , mayor que a} a A es un elemento minimal de A, si no hay c A / c < a {No existe un c A , menor que a} Teorema: Todo conjunto parcialmente ordenado no vacío y finito, tiene al menos un maximal y al menos un minimal. Máximo y mínimo de A: a A es el máximo de A, si: ( x ≤ a x A) a A es el mínimo de A, si: ( a ≤ x x A) Teorema: Todo conjunto parcialmente ordenado, tiene a lo mucho un máximo, y a lo mucho un mínimo. Si existe máximo se denota por I (elemento unidad) Si existe mínimo se denota por 0 (elemento cero) Cota superior e inferior: Dado (A, ≤ ), y dado B, un subconjunto de A: a A es una cota superior de B, si: x ≤ a x B a A es una cota inferior de B, si: a ≤ x x B

Puntos extremos Supremo e ínfimo: Dado (A, ≤ ), y dado B, un subconjunto de A: a A es el supremo de B (mínima cota superior de B), si: siendo a una cota superior de B, y siendo c una cota superior de B, entonces: a≤c a A es el ínfimo de B (máxima cota inferior de B), si: siendo a una cota inferior de B, y siendo c una cota inferior de B, entonces: c≤a b d Teorema: B tiene a lo mucho un supremo, y a lo mucho un ínfimo. a Ejm: maximal de A: a Siendo B= {c, d, e} : cota superior: c, a minimal de A: g, h c máximo de A: a cota inferior: g mínimo de A: No existe supremo: c e f ínfimo: g g h Hallar con B={b, c}, luego con B={c, f} y con B={b, c, d}

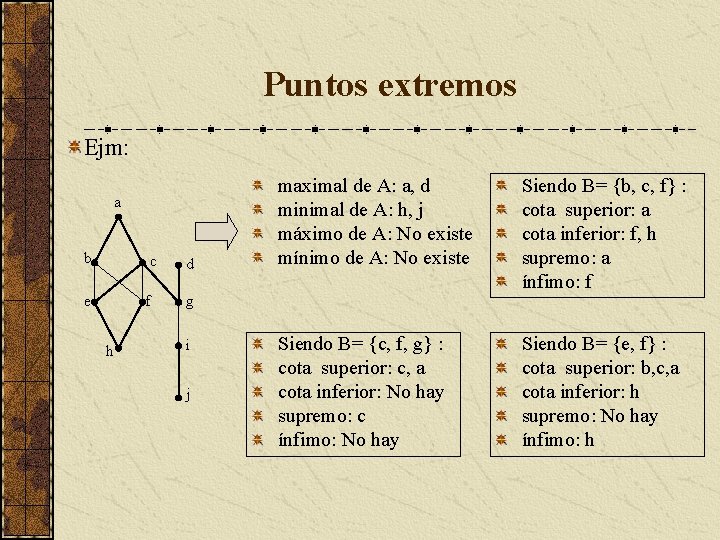
Puntos extremos Ejm: a b c d e f g h i j maximal de A: a, d minimal de A: h, j máximo de A: No existe mínimo de A: No existe Siendo B= {b, c, f} : cota superior: a cota inferior: f, h supremo: a ínfimo: f Siendo B= {c, f, g} : cota superior: c, a cota inferior: No hay supremo: c ínfimo: No hay Siendo B= {e, f} : cota superior: b, c, a cota inferior: h supremo: No hay ínfimo: h