Procesamiento Digital de Seales DSP n n Es

Procesamiento Digital de Señales (DSP) n n Es el tratamiento o manipulación de datos digitales que representan alguna señal física. Los datos son normalmente generados mediante un proceso de conversión A/D. El procesamiento se puede clasificar en dos grupos: 1. Estadístico 2. Fourier

Análisis de Fourier: Encontrar información “escondida” dentro de los datos: - Limpiarla (ruido) - Ubicar patrones - Compactarla - Reacomodarla Técnicas empleadas - Transformaciones de Fourier - Filtrado Digital - Convolución y Correlación

Aplicaciones: • Óptica • Astronomía • Geología • Análisis Químico • Materiales • Computación • Medicina • Acústica • Música • Video

Series de Fourier n Cualquier señal periódica continua se puede representar como una serie infinita de senos y cosenos de diferentes amplitudes cuyas frecuencias son harmónicas de la frecuencia de la señal. Esto es lo que se conoce como la serie de Fourier de la señal.

Una Función Periódica f(t) tiene la siguiente propiedad para todo valor de t. f(t)=f(t+T) A la constante mínima T para la cual se cumple lo anterior se le llama el periodo de la función Repitiendo la propiedad se puede obtener: f(t)=f(t+n. T), donde n=0, 1, 2, 3, . . .

Serie Trigonométrica de Fourier Las Funciones periódicas f(t) de periodo T pueden expresarse por la siguiente serie, llamada Serie Trigonométrica de Fourier f(t) = ½ a 0 + a 1 cos( 0 t)+a 2 cos(2 0 t)+. . . + b 1 sen( 0 t)+b 2 sen(2 0 t)+. . . Donde 0=2 /T. Es decir,

Es posible escribir de una manera ligeramente diferente la Serie de Fourier, si observamos que el término ancos(n 0 t)+bnsen(n 0 t) se puede escribir como Podemos encontrar una manera más compacta para expresar estos coeficientes pensando en un triángulo rectángulo:

bn qn an Con lo cual la expresión queda

Si además definimos C 0=a 0/2, la serie de Fourier se puede escribir como Así, y

Así, una función periódica f(t) se puede escribir como la suma de componentes sinusoidales de diferentes frecuencias n=n 0. A la componente sinusoidal de frecuencia n 0: Cncos(n 0 t+qn) se le llama la enésima armónica de f(t). A la primera armónica (n=1) se le llama la componente fundamental y su periodo es el mismo que el de f(t) A la frecuencia 0=2 f 0=2 /T se le llama frecuencia angular fundamental.

Cálculo de los coeficientes de la Serie Dada una función periódica f(t) ¿cómo se obtiene su serie de Fourier? Obviamente, el problema se resuelve si sabemos como calcular los coeficientes a 0, a 1, a 2, . . . , b 1, b 2, . . . Esto se puede resolver considerando la ortogonalidad de las funciones seno y coseno.

Functiones Ortogonales n Un conjunto de funciones { k} es orthogonal en el intervalo a < t < b si se cumple que

Functiones senoidales ortogonales 0=2 /T.

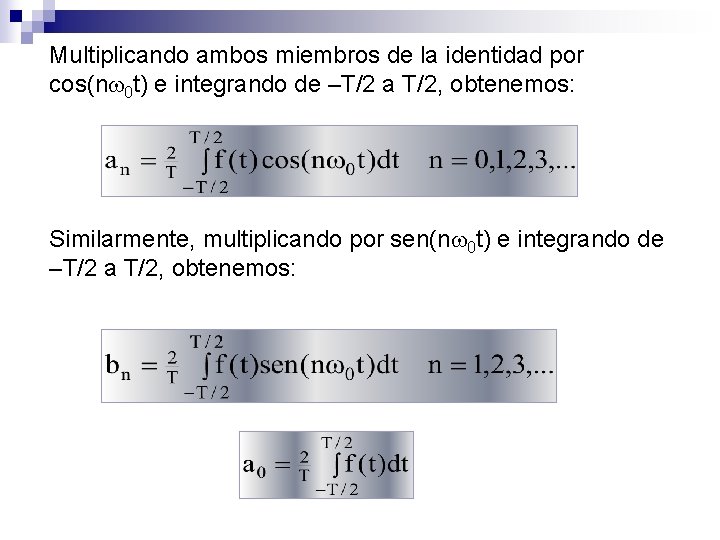
Multiplicando ambos miembros de la identidad por cos(n 0 t) e integrando de –T/2 a T/2, obtenemos: Similarmente, multiplicando por sen(n 0 t) e integrando de –T/2 a T/2, obtenemos:

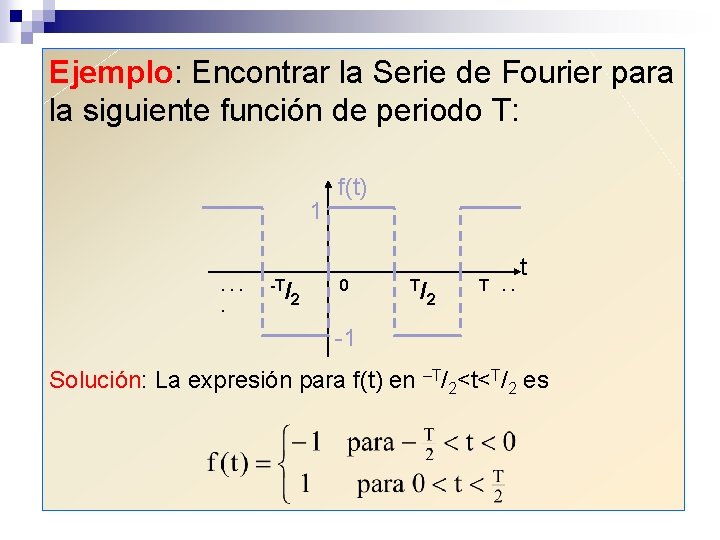
Ejemplo: Encontrar la Serie de Fourier para la siguiente función de periodo T: 1. . -T/ 2 f(t) 0 T/ 2 T. . t -1 Solución: La expresión para f(t) en –T/2<t<T/2 es

Coeficientes an:

Coeficiente a 0:

Coeficientes bn:

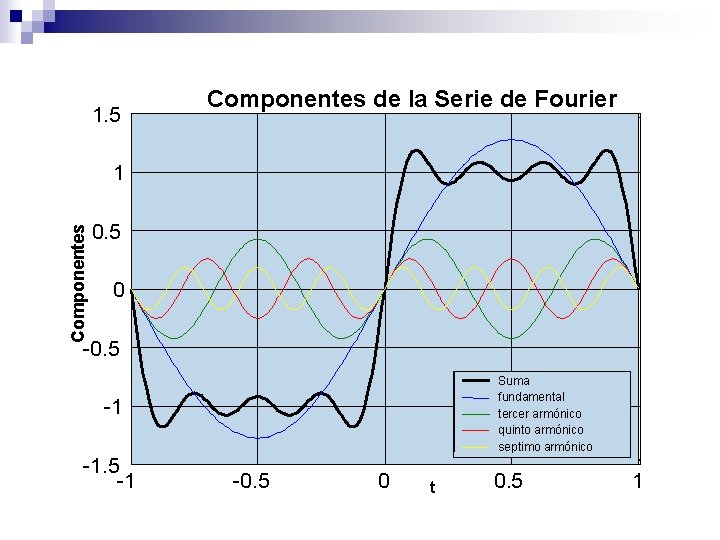
Serie de Fourier: Finalmente la Serie de Fourier queda como En la siguiente figura se muestran: la componente fundamental y los armónicos 3, 5 y 7 así como la suma parcial de estos primeros cuatro términos de la serie para 0= , es decir, T=2:

1. 5 Componentes de la Serie de Fourier Componentes 1 0. 5 0 -0. 5 Suma fundamental tercer armónico quinto armónico septimo armónico -1 -1. 5 -1 -0. 5 0 t 0. 5 1

Forma Compleja de la Serie de Fourier Consideremos la serie de Fourier para una función periodica f(t), con periodo T=2 / 0. Es posible obtener una forma alternativa usando las fórmulas de Euler: Donde

Forma Compleja de la Serie de Fourier La serie se puede escribir como O bien, Es decir, Series de Fourier. 22

A la expresión obtenida Se le llama forma compleja de la serie de Fourier y sus coeficientes cn pueden obtenerse a partir de los coeficientes an, bn como ya se dijo, o bien: Para n=0, 1, 2, 3, . . .

Espectros de Frecuencia Discreta Dada una función periódica f(t), le corresponde una y sólo una serie de Fourier, es decir, le corresponde un conjunto único de coeficientes cn. Por ello, los coeficientes cn especifican a f(t) en el dominio de la frecuencia de la misma manera que f(t) especifica la función en el dominio del tiempo.

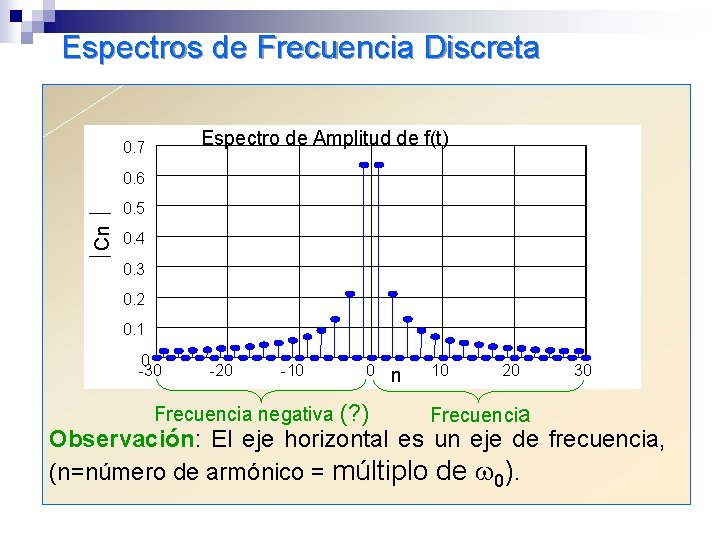
Espectros de Frecuencia Discreta Espectro de Amplitud de f(t) 0. 7 Cn 0. 6 0. 5 0. 4 0. 3 0. 2 0. 1 0 -30 -20 -10 0 Frecuencia negativa (? ) n 10 20 Frecuencia 30 Observación: El eje horizontal es un eje de frecuencia, (n=número de armónico = múltiplo de 0).

Ancho de banda de una señal n n Existen muchas definiciones para el ancho de banda de una señal, dependiendo del contexto en que se emplee el término. Una de ellas se refiere al conjunto de las componentes de frecuencia cuya amplitud no es menor en 3 d. B a la mayor componente del espectro de Fourier de la señal. Esta definición sería inapropiada si el objetivo es mantener una representación fiel de la señal. Obviamente, para una señal periódica podemos obtener su ancho de banda con su serie de Fourier.

De la Serie a la Transformada de Fourier La serie de Fourier nos permite obtener una representación en el dominio de la frecuencia para funciones periódicas f(t). ¿Es posible extender de alguna manera las series de Fourier para obtener el dominio de la frecuencia de funciones no periódicas? La respuesta es sí, pero ahora el espectro de frecuencias NO es discreto sino continuo.

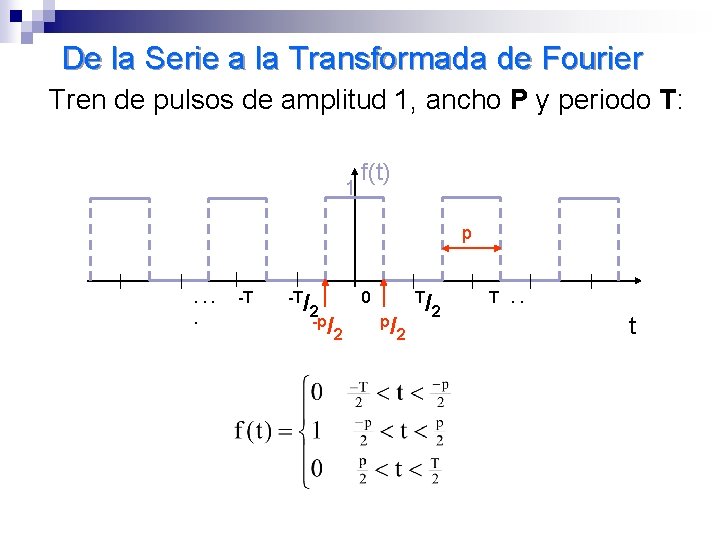
De la Serie a la Transformada de Fourier Tren de pulsos de amplitud 1, ancho P y periodo T: 1 f(t) p . . -T -T/ 2 -p/ T/ 0 2 p/ 2 2 T. . t

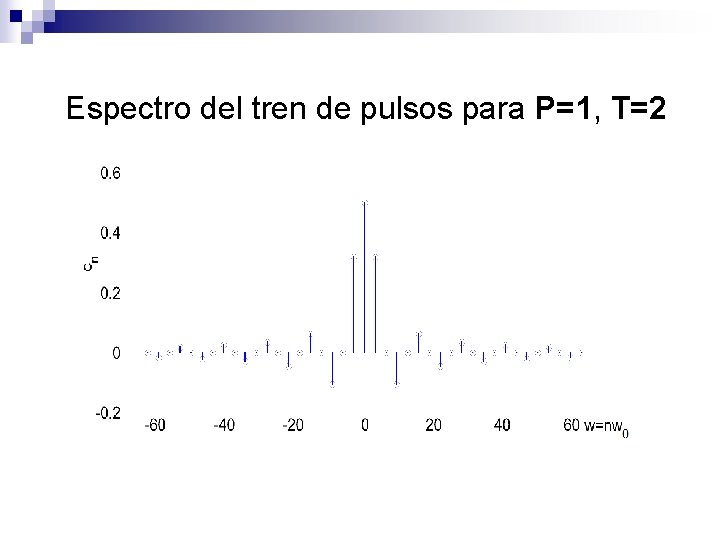
Espectro del tren de pulsos para P=1, T=2

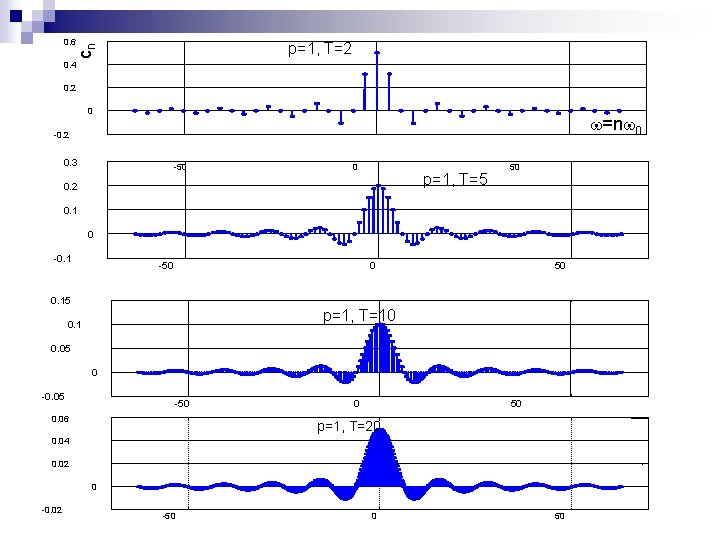
0. 6 cn p=1, T=2 0. 4 0. 2 0 =n 0 -0. 2 0. 3 -50 0 p=1, T=5 0. 2 50 0. 1 0 -0. 1 -50 0 0. 15 50 p=1, T=10 0. 1 0. 05 0 -0. 05 -50 0. 06 0 50 p=1, T=20 0. 04 0. 02 0 -0. 02 -50 0 50

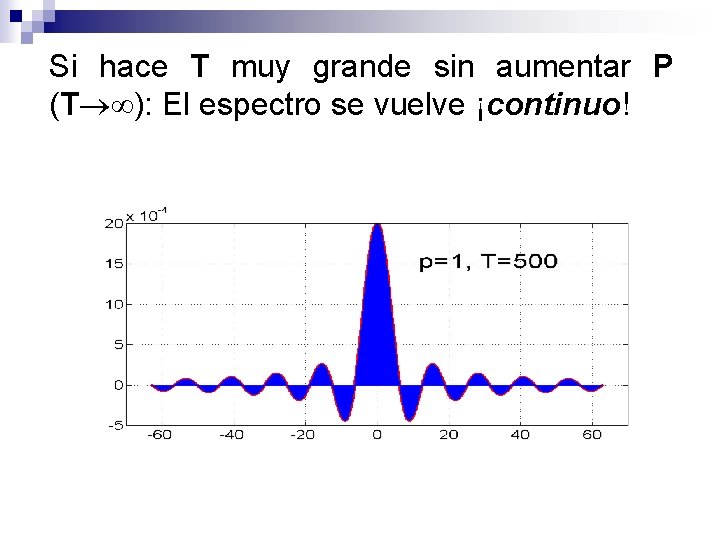
Si hace T muy grande sin aumentar P (T ): El espectro se vuelve ¡continuo!

Es decir, Transformada De Fourier Donde Identidad De Fourier Estas expresiones nos permiten calcular la expresión F( ) (dominio de la frecuencia) a partir de f(t) (dominio del tiempo) y viceversa

Notación: A la función F( ) se le llama transformada de Fourier de f(t) y se denota por F, es decir En forma similar, a la expresión que nos permite obtener f(t) a partir de F( ) se le llama transformada inversa de Fourier y se denota por F – 1 , es decir

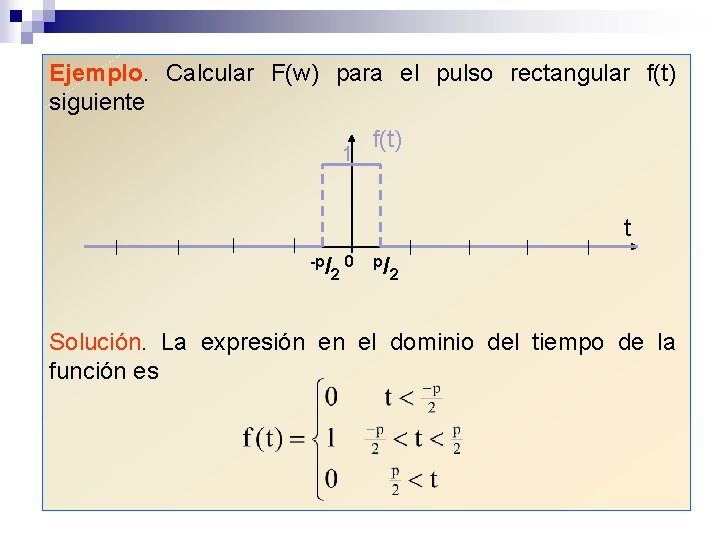
Ejemplo. Calcular F(w) para el pulso rectangular f(t) siguiente 1 f(t) t -p/ 0 2 p/ 2 Solución. La expresión en el dominio del tiempo de la función es

Integrando Usando la fórmula de Euler: Obsérvese que el resultado es igual al obtenido para cn cuando T , pero multiplicado por T.

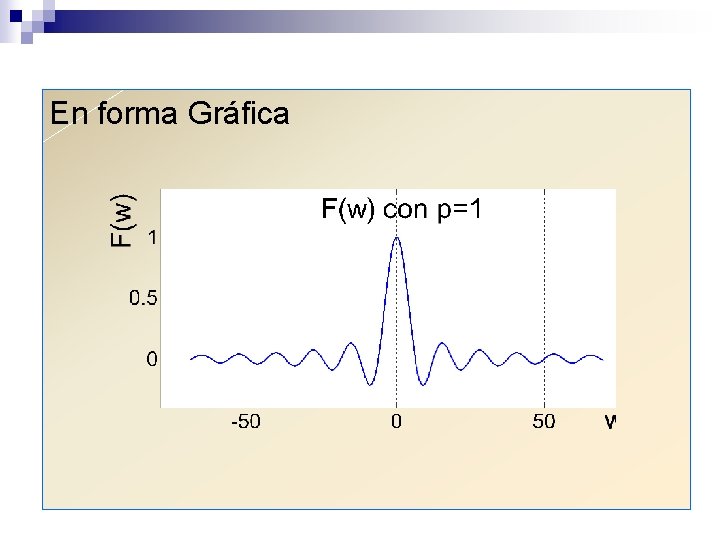
En forma Gráfica

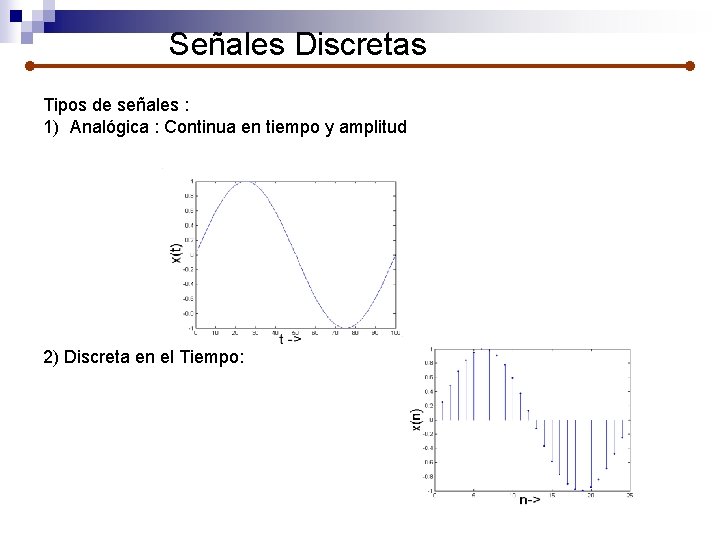
Señales Discretas Tipos de señales : 1) Analógica : Continua en tiempo y amplitud 2) Discreta en el Tiempo:

Transformada Discreta de Fourier FT: Cuando la señal de origen es continua El tiempo y la frecuencia son variables continuas Pero si las señales son discretas DTFT (Discrete Time Fourier Transform) El tiempo se discretiza pero la frecuencia sigue siendo continua (la suma es infinita)

The DFT Para discretizar ambas variables 1) Limitamos la frecuencia continua a un valor máximo value de Fs 2) Discretizamos la frecuencia a valores m La Transformada se convierte en

The DFT En donde : X(m) = la mth DFT componente de salida: X(0), X(1), X(2)… m = Indice de la salida de la DFT en el dominio de la fecuencia m = 0, 1, 2, …, N-1 x(n) = muestras de entrada, x(0), x(1), x(2)…. . n = Indice de las muestras de entrada, n = 0, 1, 2, 3, …, N-1 N = Número total de muestras de entrada y de los puntos de frecuencia en la salida de la DFT.

DFT La DFT es una cantidad compleja La magnitus de X(m) es : El ángulo de X(m) es :

DFT Ejemplo Supongamos que se desea evaluar la DFT en 8 puntos a una señal Senoidal con componenetes de frequencia de 1 KHz and 2 KHz Supongamos que: Periodo de x(t) = 1/1 Khz = 1/1000 8 muestras/periodo => Ts = 1/8000 sec O sea Fs = 8000 muestras/s t = n. Ts n = 0, 1, …, 7

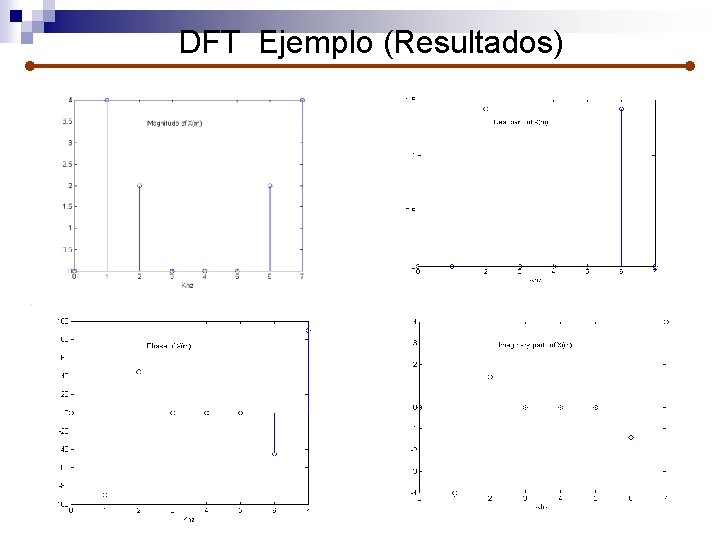
DFT Ejemplo (Cont…) Entonces Componente DC Etc. . . Evaluando se tiene: X(0) = 0 +j 0 X(2) = 1. 414 + j 1. 414 X(4) = 0 +j 0 X(6) = 1. 414 – j 1. 414 (dc) (2 Khz) (4 Khz) (6 Khz) X(1) = 0 – j 4 X(3) = 0 + j 0 X(5) = 0 + j 0 X(7) = 0 + j 4 (1 KHz) (3 Khz) (5 Khz) (7 KHz)

DFT Ejemplo (Resultados)

Simetría en la DFT Se observa que: magnitud de X(N-m) = magnitud de X(m) fase de X(N-m) = fase de X(m) O: X(m) = complejo conjugado de X(N-m) Conclusión: Al calcular la DFT de x(n) en N puntos, obtenemos N términos complejos de salida pero sólo los primeros N/2 términos son independientes

Propiedades de la DFT 1) Linealidad: si a(n) = b(n) + c(n) entonces A(m) = B(m) + C(m) 2) Teorema del corrimiento: : Si y(n) = x(n+k) entonces Y(m) = ej 2 pikm/N X(m)

Transformada Inversa IDFT Para obtener x(n) a partir de X(m)

Fugas en la DFT Las salidas de DFT corresponden a las frecuencias f = mfs/N ¿Qué sucede si la entrada tiene frecuencias que no coinciden Con esos valores Digamos que en el ejemplo anterior se tienen frecuencias 2. 3 Khz y muestreamos 8000 M/s Los picos detectados son = 0 Kkz, 1 Khz, 2 Khz, …, 7 Khz pero el pico 2. 3 Khz no aparece!! Este pico de frecuencia se ha “fugado” (escurrido) Remedio “Windowing”

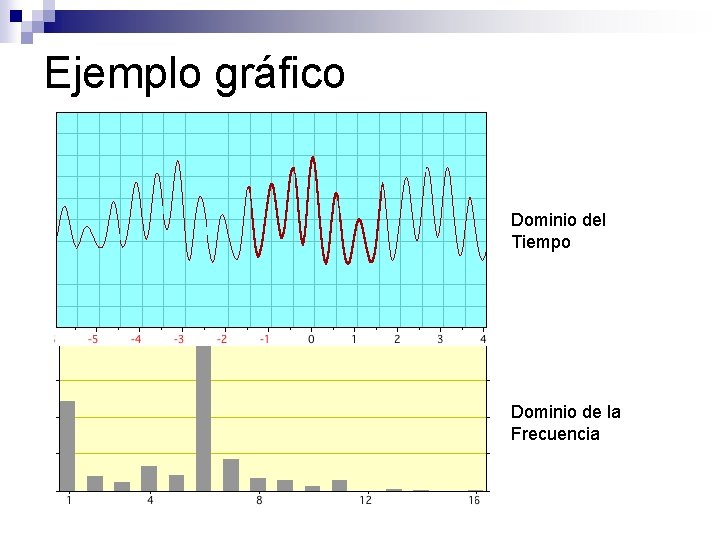
Ejemplo gráfico Dominio del Tiempo Dominio de la Frecuencia

La Transformada Discreta de Fourier (DFT) requiere el cálculo de N funciones exponenciales para obtener F(n), lo cual resulta un esfuerzo de cálculo enorme para N grande. Se han desarrollado métodos que permiten ahorrar cálculos y evaluar de manera rápida la Transformada discreta, a estos métodos se les llama Transformada Rápida de Fourier (FFT)

n En el cálculo de la transformada directa de Fourier el número de operaciones requeridas es proporcional a N 2 n En el cálculo de la transformada rápida de Fourier (FFT) el número de operaciones requeridas es proporcional a N(ln. N)

En Resumen: n n n Para encontrar el espectro de frecuencias de una señal continua y periódica empleamos su SERIE DE FOURIER Para encontrar el espectro de frecuencias de una señal continua aperiódica empleamos la TRANSFORMADA DE FOURIER Para encontrar el espectro de frecuencias de una señal discreta y periódica empleamos la DFT Para encontrar el espectro de frecuencias de una señal discreta aperiódica aproximamos con la DFT La DFT se implementa con la FFT