Cursillo de Qumica Cuntica Los principios de la

Cursillo de Química Cuántica: Los principios de la teoría de Hartree-Fock Dr. César Antonio Estrada Mendizábal Escuela de Química Departamento de Fisicoquímica 7, 8 y 9 de marzo de 2014. 1

Algunas consideraciones filosóficas • ¿Para qué la ciencia? ¿Y en nuestro medio? Fines prácticos y cognoscitivos. • Postura filosófica: el realismo. • El mundo debe explicarse por sí mismo: el materialismo. • Los entes, las cosas, y nuestro conocimiento de ellos. • La reducción analítica o análisis reductivo y el retorno dialéctico. • Los objetos concretos y los objetos científicos. • Los resultados de distintas teorías pueden coincidir con lo empírico. 2

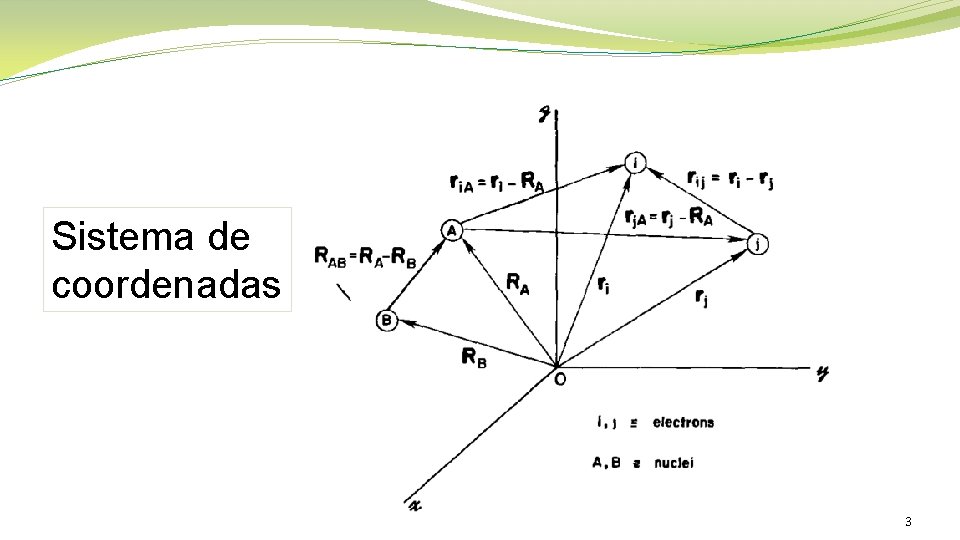
Sistema de coordenadas 3

El hamiltoniano molecular (de Coulomb) 4

La aproximación de Born-Oppenheimer 5

El movimiento nuclear 6

El principio de exclusión de Pauli Orbitales y espín-orbitales. Coordenadas: r, w, x. k: cantidad de orbitales. 7

Electrones independientes, los productos de Hartree: 8

El producto de Hartree, YHP, es una función de onda de electrones independientes, no correlacionada, pues que es la probabilidad de encontrar simultaneamente el electrón 1 en el volumen dx 1 centrado en x 1, el Electrón 2 en dx 2, etc. es igual al producto de la probabilidad de que el electrón 1 esté en dx 1 por la probabilidad de que el electrón 2 esté en dx 2, etcétera: Esto es propio de eventos independientes, no correlacionados: la probabilidad de encontrar el electrón i en un punto dado es independiente de la posición del electrón j. En la realidad, por la repulsión de cargas iguales, ambos electrones evitarán estar en el mismo lugar. YHP también distingue los electrones entre sí y no obedece el principio de Pauli. 9

Los determinantes de Slater 10

Los determinantes de Slater, los efectos de intercambio y la correlación electrónica Efectos de intercambio: se llaman así porque surgen del principio de Pauli, del intercambio de coordenadas. Los orbitales de Slater incorporan la correlación de intercambio: el movimiento de dos electrones con espín paralelo está correlacionado. El movimiento de electrones con espín opuesto no está correlacionado en los determinantes de Slater. Por eso se dice que dichos determinantes constituyen funciones de onda no correlacionadas o sin correlación electrónica. Ejemplo: Considérese un sistema de dos electrones ocupados c 1 y c 2. de espín-orbitales 11

Primer caso: los electrones tienen espín diferente u opuesto y ocupan diferentes orbitales. La probabilidad de que el electrón 1 esté en dx 1 y el electrón 2, en dx 2 viene dada por Sea P(r 1, r 2)dr 1 dr 2 la probabilidad de hallar simultaneamente el electrón 1 en el volumen dr 1 en r 1 y el electrón en dr 2 en la posición r 2: 12

Al usar la ortonormalidad de a y b : (Probabilidad de hallar el electrón 1, según y 1, en r 1) X (probabilidad de hallar el electrón 2, según y 2, en r 2) (Probabilidad de hallar el electrón 2, según y 1, en r 2) X (probabilidad de hallar el electrón 1, según y 2, en r 1) Puesto que los electrones son indistinguibles, P(r 1, r 2) es el promedio de los dos términos anteriores puede decirse que el movimiento de los dos electrones no está correlacionado. Esto se ve más claramente si y 1 = y 2, el mismo orbital, pues en este caso 13

Si se considera el mismo punto en el espacio, r 1=r 2 , y se sustituye en se ve que P(r 1, r 2) ≠ 0 : hay una probabilidad finita de hallar dos electrones de espín opuesto en el mismo punto. Segundo caso: Los dos electrones tienen el mismo espín, digamos b. Al sustituir en y en se obtiene: 14

Novedad: el término cruzado: Las probabilidades ya no son independientes, hay correlación. Si se considera el mismo punto, r 1 = r 2, P(r 1, r 1) = 0 La probabilidad de encontrar dos electrones del mismo espín en el mismo punto es cero. 15

En resumen, una función de onda electrónica Y en forma de determinante de Slater ya incluye cierta correlación electrónica, la de electrones con el mismo espín. No obstante, los electrones con espín contrario o diferente no muestran correlación. 16

La aproximación de Hartree-Fock Sistema de N electrones. Función variacional: La mejor función de onda Y 0 es la que minimiza E 0. H es el hamiltoniano electrónico. 17

La forma de los espín-orbitales se elige de modo que se minimice E 0. Se obtiene la ecuación de Hartree-Fock: f(i) es el operador de Fock y depende de un solo electrón. es el potencial promedio que sufre el electrón i por la presencia de los demás electrones. 18

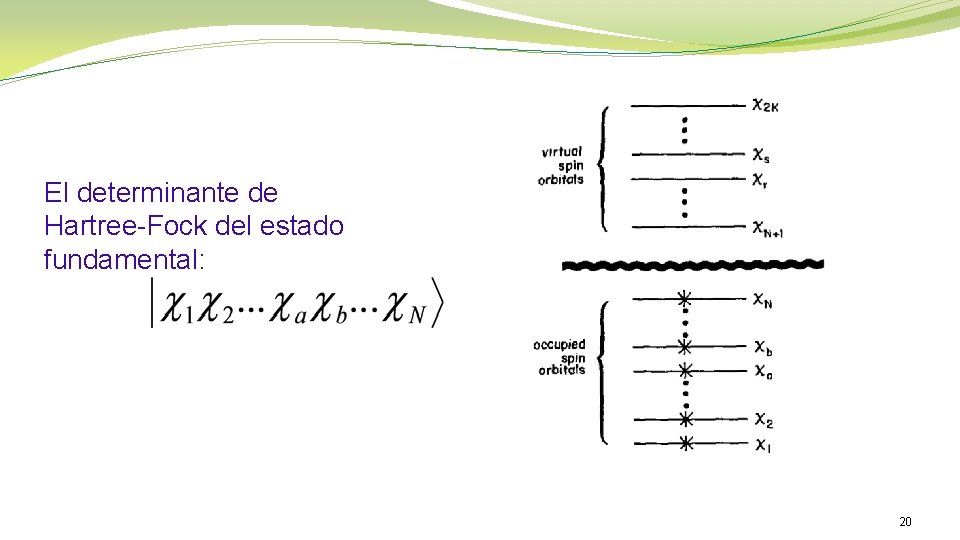
Solución de la ecuación de Fock: espín-orbitales ortonormales de energía. Los N orbitales-espín de menor energía se dicen ocupados (N es el número de electrones). El determinante de Slater correspondiente es la función de onda de Hartree-Fock del estado fundamental. 19

El determinante de Hartree-Fock del estado fundamental: 20

En principio, hay infinitas soluciones c a la ecuación de Hartree-Fock En la práctica, se introduce un conjunto finito de K funciones de base espaciales para expandir los orbitales espaciales ya(r) y yb(r): y obtener los coeficientes Cmi mediante una ecuación matricial de valores propios (las ecuaciones de Roothan). 21

Una base de K funciones espaciales {fm} da: • Un conjunto de 2 K espín-orbitales (K con espín a y K con espín b). • Lo cual da lugar a N (número de electrones) espín-orbitales ocupados, {ca}, y a 2 K – N espín-orbitales vacíos o virtuales {cr}. A mayor K, cantidad de funciones básicas, la base es más completa, y el valor esperado de la energía es menor. Límite de Hartree-Fock: E 0 cuando K es muy grande (base completa). 22

Determinantes excitados Tenemos 2 K espín orbitales y sólo se llenan N. Uno es el del estado fundamental. Se forma con los ca de menor energía. La cantidad de determinantes que se pueden formar es: 23

Los determinantes de Slater como base de la función de onda electrónica : interacción de configuraciones. Toda función antisimétrica de varias variables se puede expandir en términos de de los determinantes formados de un conjunto completo de funciones de una variable {ci}: 24

El conjunto infinito de determinantes de N electrones es una base completa para expandir cualquier función de onda de N electrones, . Formados a partir de un conjunto de espín-orbitales {ci} Sus energías exactas son eigenvalores de la matriz hamiltoniana de elementos, formada a partir del conjunto completo. Al menor eigenvalor de del estado fundamental. Energía de correlación: se le llama E 0 y es la energía exacta Ecorrel = E 0 – E 0 25

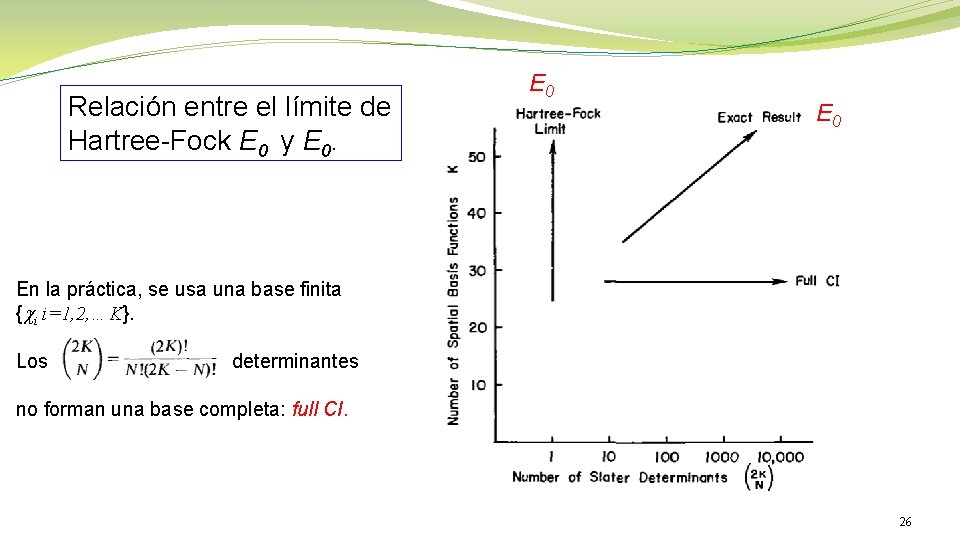
Relación entre el límite de Hartree-Fock E 0 y E 0 En la práctica, se usa una base finita {ci i=1, 2, …K}. Los determinantes no forman una base completa: full CI. 26

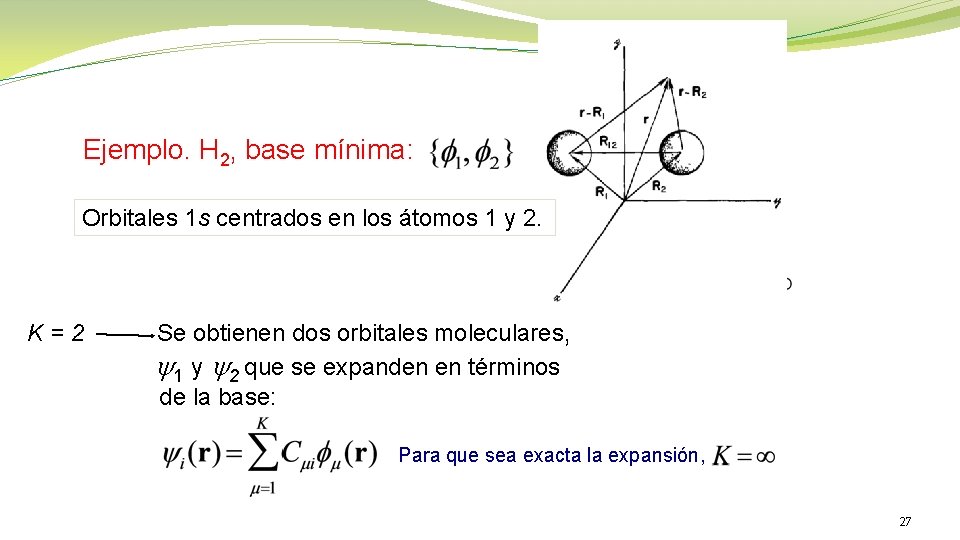
Ejemplo. H 2, base mínima: Orbitales 1 s centrados en los átomos 1 y 2. K=2 Se obtienen dos orbitales moleculares, y 1 y y 2 que se expanden en términos de la base: Para que sea exacta la expansión, 27

Se obtienen cuatro espín-orbitales: El estado fundamental de Hartree-Fock de este modelo es el determinante: 28

Interacción de configuraciones del H 2: base mínima, CI completa N = 2, 2 K = 4 Se pueden formar determinantes. 29

La función de onda exacta (en la base mínima) del estado fundamental es Los coeficientes y el valor de la energía exacta la matriz de CI completa: se encuentra diagonalizando Elementos matriciales entre determinantes como 30

Elementos matriciales de operadores entre determinantes de Slater • Los determinantes de Slater se constituyen por orbitales ortonormales {ci}. • Dado un operador O y dos determinantes de N electrones elemento matricial de O en la base de dichos determinantes y se quiere calcular el. • El cálculo se reduce a evaluar integrales entre operadores de uno o dos electrones y los espín-orbitales {ci} –y finalmente orbitales espaciales yi– ocupados en y. Ejemplo: H 2, base mínima, considérese el cálculo del elemento : 31

El hamiltoniano electrónico de un sistema de dos electrones es: Definimos: 32

Se llega a ya Donde se usó una notación especial para las integrales de uno y de dos electrones. 33

Notación de integrales de uno y de dos electrones 34

Elementos matriciales entre determinantes en términos de espín-orbitales: operadores de un electrón, . 35

Elementos matriciales entre determinantes en términos de espín-orbitales: operadores de dos electrones. 36

Ahora se pueden calcular elementos matriciales entre determinantes como, por ejemplo, el que da la energía del estado fundamental de Hartree-Fock: Efectos cuánticos Átomos independientes Notación química Repulsión electrónica Notación física Cada electrón a contribuye a E 0 con y cada par distinto ab con . 37

Reducción de espín-orbitales a orbitales espaciales Se integra sobre la variable de espín, w, tomando en cuenta la ortonormalidad de las funciones de espín, a(w) y b(w): Por ejemplo: 38

De esta forma, generalizando se obtienen las siguientes reducciones: Integrales de un electrón Integrales de dos electrones Las demás combinaciones de barras dan como resultado cero. 39

Generalización: considérese un sistema de un número par N de electrones: La función de onda de Hartree-Fock restringida, de capa cerrada es Restringida: los orbitales espaciales se restringen a ser los mismos para los espines a y b. Capa cerrada: cada orbital espacial está doblemente ocupado. Ocupado es una forma de hablar. Simplemente se refiere a que a un electrón le corresponde un orbital yi determinado. 40

La energía del estado fundamental de Hartree-Fock de capa cerrada, |Y 0>, es En términos de espín-orbitales y al aplicar las reglas anteriores se convierte en En términos de orbitales espaciales ¿Cuál es la interpretación física de esta energía? 41

Primero, consideremos los términos de un electrón: que es el promedio de la energía cinética y de la energía potencial de atracción nuclear de un electrón. Ahora, la integral de dos electrones que es la repulsión de Coulomb entre las distribuciones o nubes de carga y . Integral de Coulomb 42

Finalmente, considérse la integral de dos electrones que no tiene interpretación clásica. Proviene del principio de Pauli: es invariante respecto a Pij. Integral de intercambio Es decir, la interpretación es: Electrones independientes Efecto cuántico Repulsión entre pares electrónicos 43

La aproximación de Hartree-Fock Función variacional. Sistema de N electrones. La mejor función de onda Y 0 es la que minimiza E 0. H es el hamiltoniano electrónico. 44

Se varían sistemáticamente los espín-orbitales {ca} con la condición de ortonormalidad 45

Se obtiene la ecuación integro-diferencial de Hartree-Fock: donde es la energía cinética y la energía potencial de atracción de un electrón cualquiera, representado por el 1. Las dos sumatorias representan las interacciones electrónicas. En ausencia de ellas se obtiene la ecuación de Schrodinger que da los espín-orbitales de un electrón: 46

Base física del método de Hartree-Fock Como muestra la ecuación de Hartree-Fock el electrón 1 en ca está bajo el efecto del potencial de Coulomb de un electrón: Si suponemos que el electrón 2 ocupa el espín-orbital ca al integrar según las coordenadas x 2, se sustituye la interacción instantánea y concreta entre el electrón 1 y el 2 por la interacción del electrón 1 con el promedio de las posiciones del electrón 2. Al sumar sobre todos los demás, se obtiene el potencial del electrón 1 debido a la presencia de los demás N-1 electrones. 47

La forma de la ecuación de Hartree-Fock se puede cambiar si se definen ciertos operadores: Operador de Coulomb Operador de intercambio Operador de Fock Potencial de Hartree-Fock Ecuación de Hartree-Fock 48

Seguiremos el método de Hartree-Fock limitándonos a determinantes restringidos de capa cerrada: Consideremos un conjunto de K orbitales espaciales ortonormales Se puede formar un conjunto de 2 K espín-orbitales, orbital por a o por b : , multiplicando cada Espín-orbitales restringidos Determinante de capa cerrada: Es aquél en que cada orbital espacial está doblemente ocupado. O sea, si aparece el orbital yi, el determinante incluye los espín orbitales yia y yib. 49

Con este conjunto de orbitales restringidos, el estado fundamental restringido y de capa cerrada es: Cambiemos la forma de la ecuación de Hartree-Fock convirtiendo los espín-orbitales, ci(x) , en orbitales espaciales, yi (r): se integran las funciones de espín. Ecuación de Hartree-Fock en términos de orbitales. Energía de Hartree-Fock de capa cerrada 50

Introducción de una base: las ecuaciones de Roothaan La ecuación integro-diferencial de Hartree-Fock se convierte en una ecuación matricial. Se introduce una base, un conjunto de K funciones básicas para expandir linealmente los orbitales moleculares buscados, yi(r): El problema de calcular los orbitales moleculares de Hartree-Fock se reduce a calcular el conjunto de coeficientes de la expansión, Cmi. 51

Se obtiene una ecuación matricial de los Cmi al sustituir la expansión lineal de los yi en la ecuación de Hartree-Fock: Si se multiplica esta ecuación por, por la izquierda, por integrodiferencial en una ecuación matricial: y se integra, convertimos la ecuación que con las definiciones apropiadas adquiere la forma más claramente matricial: 52

Estas son las ecuaciones de Roothaan, que se pueden escribir de forma más compacta como: Matriz de Fock Matriz de traslape Matriz de los coeficientes de expansión Matriz de las energías 53

Con el objeto ya de efectuar los cálculos se hace necesario definir algunos nuevos términos. Si se tiene un electrón descrito por la función de onda espacial, ya(r): da la probabilidad de encontrar al electrón en el volumen dr localizado en r. Es la función de distribución de probabilidad o densidad de carga. La densidad total de carga de una molécula de capa cerrada descrita por un determinante de orbitales moleculares ocupados ya es: 54

Si sustituimos la expansión obtenemos: donde se define la matriz de densidad por medio de sus elementos Pmn: En los cálculos, se usa el que la matriz de densidad, en una base determinada, defina a la densidad de carga. 55

Expresión de la matriz de Fock, F, y la matriz de dos electrones G, Gmn La matriz de Fock, F, es la representación matricial del operador de Fock, f : en la base {fm}: Al aplicar la expansión en términos de la base, se obtiene: 56

Los cálculos de Hartree-Fock o el procedimiento de campo auto-consistente Las ecuaciones de Roothaan simplifican su forma si la matriz de traslape S es unitaria: Como se indica, la matriz de Fock, F, depende de la matriz C, o sea, la ecuación es no lineal y requiere un método iterativo para su solución. 57

El procedimiento del campo auto-consistente 1. Se especifica la molécula, es decir, las posiciones nucleares {RA}, los números atómicos {ZA}, el número de electrones, N, y se elige la base, {fm}. 2. Se calculan todas las integrales moleculares necesarias, Smn, H coremn y (mn|ls). 3. Se da un valor inicial aproximado de la matriz de densidad, P, y se calcula la matriz G y tomando en cuenta P y las integrales de dos electrones (mn|ls). 4. Calcúlese la matriz de Fock expansión C y la matriz de energías, e. y diagonalícese para hallar la matriz de coeficientes de 5. Fórmese una nueva matriz de densidad P a partir de la matriz C recién calculada. 6. Véase si la matriz P ha convergido. Si no, vuélvase al punto 3 para calcular la matriz G y repetir el ciclo. 7. Si P ya convergió, se toman los últimos resultados de las matrices C y e. Con ellos, se pueden calcular valores esperados de propiedades físicas y otras variables de interés. 58

Las funciones de base y las integrales Se pueden usar muchas clases de conjuntos de base {fm}. Los más usados son los orbitales de Slater y las funciones gausianas. Orbitales de Slater Funciones gausianas Los orbitales de Slater describen mejor las características cualitativas de los orbitales moleculares y se necesita menos de los primeros en los conjuntos de base, pero complican las integraciones. Las funciones gausianas simplifican las integraciones. 59

Solución: se usa como base un conjunto de orbitales de Slater, cada uno de los cuales se aproxima –se expande – en términos de gausianas: Las integrales de uno o de dos electrones se efectúan entre las gausianas primitivas: Las integraciones implican las propiedades de las funciones gausianas, la función delta de Dirac, las transformadas de Fourier y la función de error entre otras nociones matemáticas. 60

Finalmente, tómese en cuenta que se suele usar el sistema de unidades atómicas en el cual la masa y la carga del electrón son 1. Pseudoátomos: los electrones pueden sustituirse por partículas con carga y masa diferentes que pueden ser variables. Debe revisarse el código de los programas de cálculos de Hartree-Fock y hacer los cambios correspondientes. 61