Cost Revenue Profit The Cost Function The Cost



















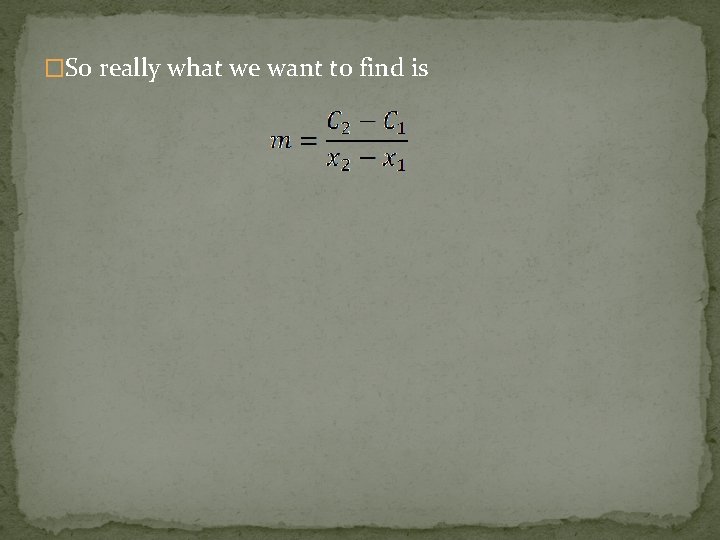
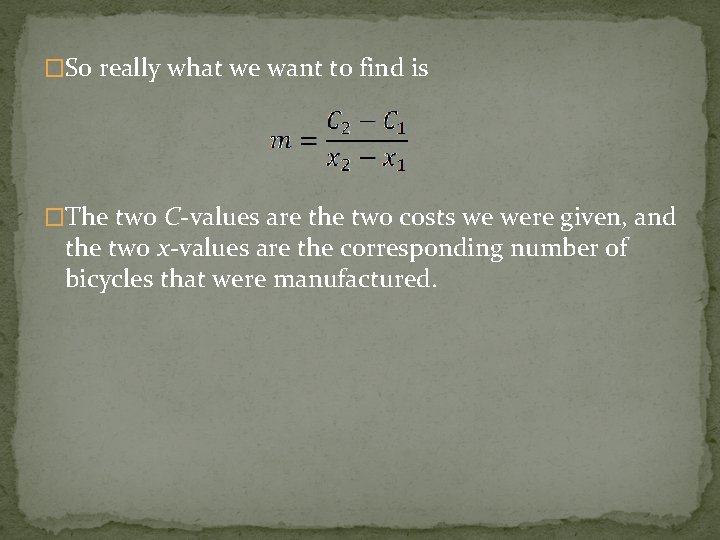
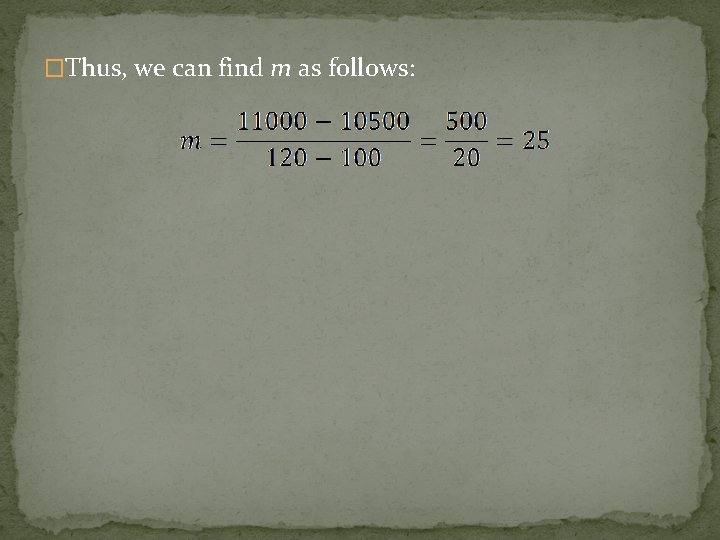



























- Slides: 51

Cost, Revenue, & Profit

The Cost Function

The Cost Function �This function gives C, the total cost to produce x units of output.

The Cost Function �This function gives C, the total cost to produce x units of output. �We deal with linear costs functions in this class, which have the form C(x)=mx+b.

The Cost Function �This function gives C, the total cost to produce x units of output. �We deal with linear costs functions in this class, which have the form C(x)=mx+b. �There are two kinds of cost associated with a cost function. They are fixed costs and variable costs.

�Variable cost is represented by mx in the equation C(x)=mx+b. Variable cost changes depending on how many units are manufactured. The more you units x that you manufacture, the higher the cost C.

�Variable cost is represented by mx in the equation C(x)=mx+b. Variable cost changes depending on how many units are manufactured. The more you units x that you manufacture, the higher the cost C. �Fixed cost is represented by b in the equation C(x)=mx+b. Fixed costs do not depend on the number of unit manufactured. Examples of fixed costs are rent, utility bills, and employee wages. You have to pay these costs regardless of how many units you manufacture.

�As an example, imagine you own a business that produces only one product, widgets.

�As an example, imagine you own a business that produces only one product, widgets. �Suppose your fixed costs (rent, electricity, etc. ) amount to $100 per month, and that it costs you $0. 20 (20 cents) to produce each widget.

�As an example, imagine you own a business that produces only one product, widgets. �Suppose your fixed costs (rent, electricity, etc. ) amount to $100 per month, and that it costs you $0. 20 (20 cents) to produce each widget. �Your cost function would then be C(x)=0. 20 x+100. Note that the cost to produce each unit is also known as the marginal cost, so here the marginal cost is $0. 20.

�We can use the cost function to determine the total cost to produce any number of widgets, where x represents the number of widgets produced.

�We can use the cost function to determine the total cost to produce any number of widgets, where x represents the number of widgets produced. �For example, to determine what the cost would be to produce 500 widgets, we would find C(500)=0. 20(500)+100=200. Thus, it would cost $200 to produce 500 widgets.

�To summarize: A linear cost function has the form C(x)=mx+b, where mx is called the variable cost, b is called the fixed cost, and m is called the marginal cost. Notice that the marginal cost is just the slope of the linear function. A common interpretation of marginal cost is “the cost to produce one more item”.

�To summarize: A linear cost function has the form C(x)=mx+b, where mx is called the variable cost, b is called the fixed cost, and m is called the marginal cost. Notice that the marginal cost is just the slope of the linear function. A common interpretation of marginal cost is “the cost to produce one more item”. �Variable cost varies depending on the number of units x that are produced. The more units produced, the higher the cost.

�A common problem is to find the cost function if you know how much it costs to produce two different quantities of a product.

�A common problem is to find the cost function if you know how much it costs to produce two different quantities of a product. �For example, suppose a bicycle factory can produce 100 bicycles in a day at a cost of $10, 500 and it can produce 120 bicycles at a cost of $11, 000. Find the cost function for the bicycle factory.

�A common problem is to find the cost function if you know how much it costs to produce two different quantities of a product. �For example, suppose a bicycle factory can produce 100 bicycles in a day at a cost of $10, 500 and it can produce 120 bicycles at a cost of $11, 000. Find the cost function for the bicycle factory. �We want to find a function C(x)=mx+b that matches this data. This means we need to find m and b, the marginal and the fixed costs.

�We can do this by remembering the definition of slope Recall that the definition of slope is

�We can do this by remembering the definition of slope Recall that the definition of slope is �However, in our equation we don’t have x and y, we have x and C, where x represents the number of bicycles manufactured, and C represents the cost to manufacture the bicycles.
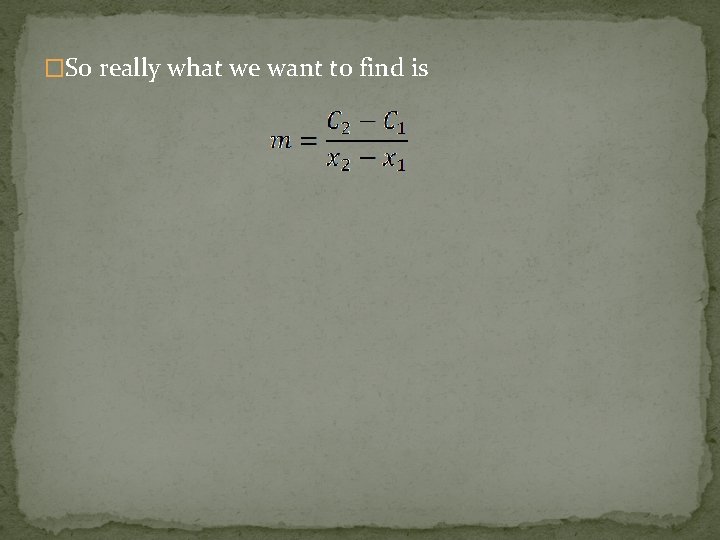
�So really what we want to find is
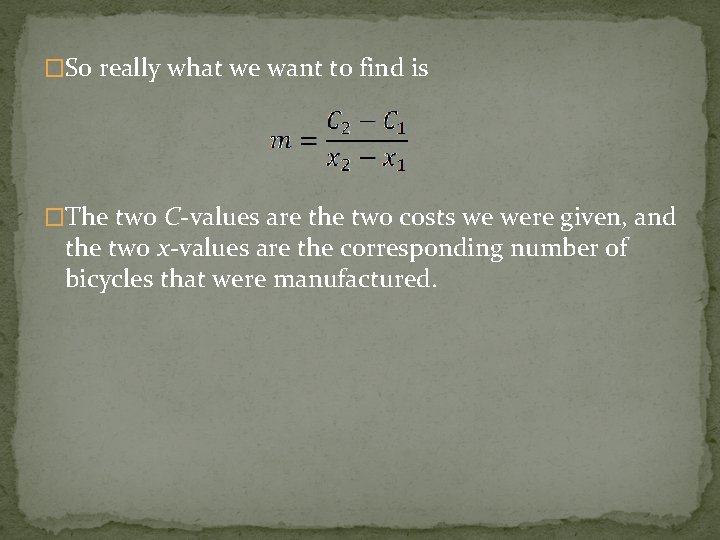
�So really what we want to find is �The two C-values are the two costs we were given, and the two x-values are the corresponding number of bicycles that were manufactured.
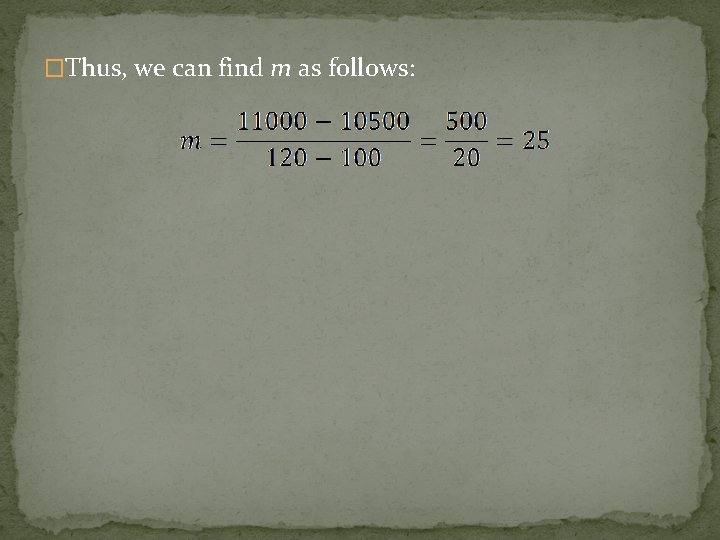
�Thus, we can find m as follows:

�Thus, we can find m as follows: �So the marginal cost is $25. This can be interpreted to mean that it costs $25 to manufacture each bicycle.

�Thus, we can find m as follows: �So the marginal cost is $25. This can be interpreted to mean that it costs $25 to manufacture each bicycle. �So far we have C(x)=25 x+b. Now we just have to find b.

�Thus, we can find m as follows: �So the marginal cost is $25. This can be interpreted to mean that it costs $25 to manufacture each bicycle. �So far we have C(x)=25 x+b. Now we just have to find b. �We can do this by using the information that we started with. We can plug in 11, 00 o for C and 120 for x, and then solve for b.

�This gives 11000=25(120)+b, and this means b=8000. The fixed costs are $8, 000.

�This gives 11000=25(120)+b, and this means b=8000. The fixed costs are $8, 000. �Thus, our cost equation is C(x)=25 x+8000. We can now use this equation to find out how much it would cost to manufacture any number of bicycles.

�What does a linear cost function look like when you graph it?

�What does a linear cost function look like when you graph it? �Let’s go back to our widget example. We put the number of units produced (represented by x) on the x -axis, and the cost C on the C-axis (what would normally be the y-axis).

�What does a linear cost function look like when you graph it? �Let’s go back to our widget example. We put the number of units produced (represented by x) on the x -axis, and the cost C on the C-axis (what would normally be the y-axis).

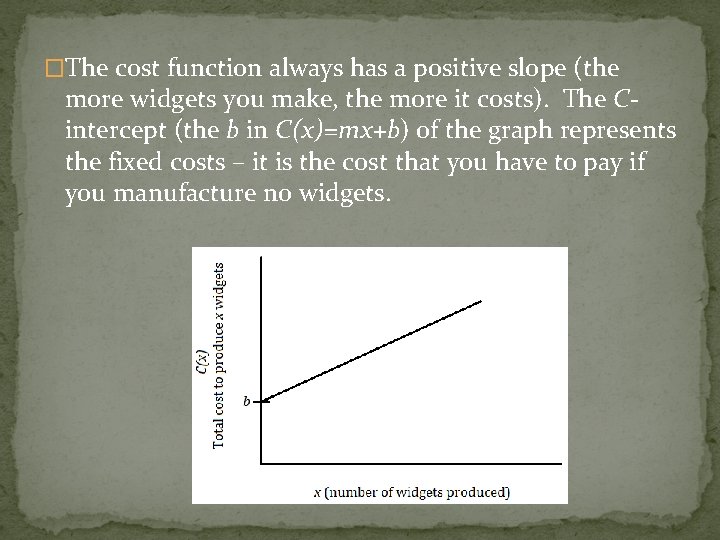
�The cost function always has a positive slope (the more widgets you make, the more it costs). The Cintercept (the b in C(x)=mx+b) of the graph represents the fixed costs – it is the cost that you have to pay if you manufacture no widgets.

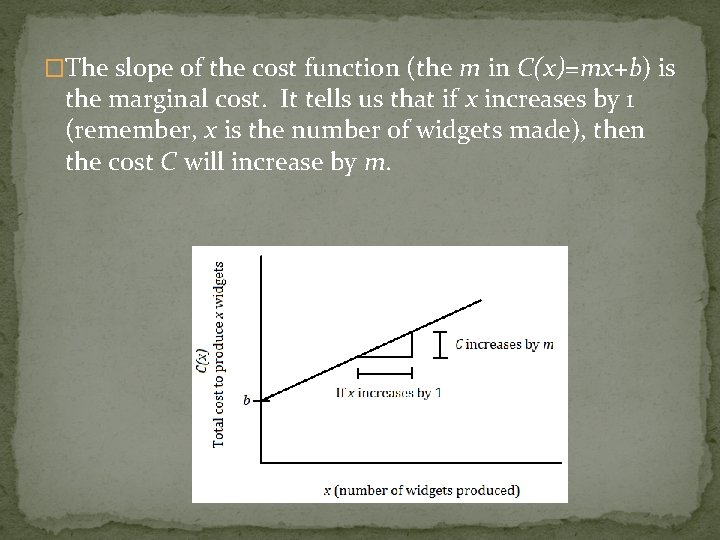
�The slope of the cost function (the m in C(x)=mx+b) is the marginal cost. It tells us that if x increases by 1 (remember, x is the number of widgets made), then the cost C will increase by m.

The Revenue Function

The Revenue Function �This function gives R, the total revenue generated by selling x units.

The Revenue Function �This function gives R, the total revenue generated by selling x units. �For now we examine linear revenue functions. They have the form R(x)=mx, where m is the price per unit, and x is the number of units sold.

The Revenue Function �This function gives R, the total revenue generated by selling x units. �For now we examine linear revenue functions. They have the form R(x)=mx, where m is the price per unit, and x is the number of units sold. �This tells us that revenue is equal to the number of units that you sell multiplied by the price that you charge for each unit. Hopefully this makes some intuitive sense – revenue is equal to price times quantity!

�For example, suppose you have a store that sells widgets, and that you charge $0. 40 per widget.

�For example, suppose you have a store that sells widgets, and that you charge $0. 40 per widget. �Your revenue function would be R(x)=0. 40 x. You can then use this function to determine exactly how much revenue you would make if you sold any number of widgets.

�For example, suppose you have a store that sells widgets, and that you charge $0. 40 per widget. �Your revenue function would be R(x)=0. 40 x. You can then use this function to determine exactly how much revenue you would make if you sold any number of widgets. �For example, if you sold 1000 widgets one day, your revenue for that day would be R(1000)=0. 40(1000)=$400.

The Profit Function

The Profit Function �This function gives P, the total profit generated by selling x units.

The Profit Function �This function gives P, the total profit generated by selling x units. �Profit is defined to be Revenue minus Cost, or in function form, P(x)=R(x)-C(x) or simply P=R-C.

The Profit Function �This function gives P, the total profit generated by selling x units. �Profit is defined to be Revenue minus Cost, or in function form, P(x)=R(x)-C(x) or simply P=R-C. �Hopefully this makes some intuitive sense as well. To calculate profit, you take the amount of money that you bring in by selling a product (revenue), and subtract the amount you spent to make that product (cost).

�Profit can either be positive or negative. A positive profit means that R>C, while a negative profit (often called a loss) means that R<C. If R=C, you break even.

�Profit can either be positive or negative. A positive profit means that R>C, while a negative profit (often called a loss) means that R<C. If R=C, you break even. �For example, suppose you have company that manufactures and also sells widgets. Suppose your cost function is C(x)=0. 20 x+100 and your revenue function is R(x)=0. 40 x (this means it costs you $0. 20 to manufacture each widget, plus fixed costs of $100, and you sell the widgets for $0. 40 each).

�Profit can either be positive or negative. A positive profit means that R>C, while a negative profit (often called a loss) means that R<C. If R=C, you break even. �For example, suppose you have company that manufactures and also sells widgets. Suppose your cost function is C(x)=0. 20 x+100 and your revenue function is R(x)=0. 40 x (this means it costs you $0. 20 to manufacture each widget, plus fixed costs of $100, and you sell the widgets for $0. 40 each). �Your profit function would then be P(x)=R(x)-C(x) or P(x)=0. 40 x-(0. 20 x+100)=0. 20 x-100.

�A common question is to find the number of units that you must sell in order to break even. There are two ways to answer this question.

�A common question is to find the number of units that you must sell in order to break even. There are two ways to answer this question. �You can either set revenue equal to cost and solve for x, or you can set profit equal to zero and solve for x. Either way will give you the same answer.

�A common question is to find the number of units that you must sell in order to break even. There are two ways to answer this question. �You can either set revenue equal to cost and solve for x, or you can set profit equal to zero and solve for x. Either way will give you the same answer. �For example, we could find the break even point for our widget profit function P(x)=0. 20 x-100 by setting it equal to zero and solving for x:

�A common question is to find the number of units that you must sell in order to break even. There are two ways to answer this question. �You can either set revenue equal to cost and solve for x, or you can set profit equal to zero and solve for x. Either way will give you the same answer. �For example, we could find the break even point for our widget profit function P(x)=0. 20 x-100 by setting it equal to zero and solving for x: � 0. 20 x-100=0, add 100 to both sides, get 0. 20 x=100, then divide both sides by 0. 20 and get x=500. So we must sell 500 widgets to break even. Any amount more than 500 means we will make a profit, and any less, a loss.

�You can read more about cost, revenue, and profit functions on the worksheet at http: //www. math. utep. edu/Faculty/cmmundy/Math %201320/Worksheets/Section%201. 2. pdf
 Cost revenue and profit functions
Cost revenue and profit functions Lesson 3 cost revenue and profit maximization
Lesson 3 cost revenue and profit maximization Profit maximization
Profit maximization Economic profit vs accounting profit
Economic profit vs accounting profit Post acquisition profit is which profit
Post acquisition profit is which profit Rumus penerimaan
Rumus penerimaan The relative proportion of variable fixed or mixed
The relative proportion of variable fixed or mixed Average revenue vs marginal revenue
Average revenue vs marginal revenue Aplikasi fungsi kuadrat
Aplikasi fungsi kuadrat Assumptions for cvp analysis
Assumptions for cvp analysis Desired sales formula
Desired sales formula Cvp analysis assumptions
Cvp analysis assumptions When graphing cost-volume-profit data on a cvp chart:
When graphing cost-volume-profit data on a cvp chart: Cost volume profit analysis graph
Cost volume profit analysis graph Objectives of cost volume profit analysis
Objectives of cost volume profit analysis 2-5 graphs of expense and revenue functions answer key
2-5 graphs of expense and revenue functions answer key What is marginal revenue formula
What is marginal revenue formula Seberapa penting pemeriksaan atas laba rugi
Seberapa penting pemeriksaan atas laba rugi Price is greater than marginal cost in monopoly
Price is greater than marginal cost in monopoly Hát kết hợp bộ gõ cơ thể
Hát kết hợp bộ gõ cơ thể Ng-html
Ng-html Bổ thể
Bổ thể Tỉ lệ cơ thể trẻ em
Tỉ lệ cơ thể trẻ em Voi kéo gỗ như thế nào
Voi kéo gỗ như thế nào Tư thế worms-breton
Tư thế worms-breton Hát lên người ơi alleluia
Hát lên người ơi alleluia Kể tên các môn thể thao
Kể tên các môn thể thao Thế nào là hệ số cao nhất
Thế nào là hệ số cao nhất Các châu lục và đại dương trên thế giới
Các châu lục và đại dương trên thế giới Công thức tiính động năng
Công thức tiính động năng Trời xanh đây là của chúng ta thể thơ
Trời xanh đây là của chúng ta thể thơ Cách giải mật thư tọa độ
Cách giải mật thư tọa độ Làm thế nào để 102-1=99
Làm thế nào để 102-1=99 độ dài liên kết
độ dài liên kết Các châu lục và đại dương trên thế giới
Các châu lục và đại dương trên thế giới Thể thơ truyền thống
Thể thơ truyền thống Quá trình desamine hóa có thể tạo ra
Quá trình desamine hóa có thể tạo ra Một số thể thơ truyền thống
Một số thể thơ truyền thống Cái miệng nó xinh thế chỉ nói điều hay thôi
Cái miệng nó xinh thế chỉ nói điều hay thôi Vẽ hình chiếu vuông góc của vật thể sau
Vẽ hình chiếu vuông góc của vật thể sau Nguyên nhân của sự mỏi cơ sinh 8
Nguyên nhân của sự mỏi cơ sinh 8 đặc điểm cơ thể của người tối cổ
đặc điểm cơ thể của người tối cổ Ví dụ về giọng cùng tên
Ví dụ về giọng cùng tên Vẽ hình chiếu đứng bằng cạnh của vật thể
Vẽ hình chiếu đứng bằng cạnh của vật thể Fecboak
Fecboak Thẻ vin
Thẻ vin đại từ thay thế
đại từ thay thế điện thế nghỉ
điện thế nghỉ Tư thế ngồi viết
Tư thế ngồi viết Diễn thế sinh thái là
Diễn thế sinh thái là Dot
Dot Các số nguyên tố
Các số nguyên tố