COMPUTER GRAPHIC Output Primitif dan Algoritma Garis e

COMPUTER GRAPHIC Output Primitif dan Algoritma Garis e. Johanes I. Karokaro 181401016 Dwi Martin Sinambela 181401040 Dicky A. Manurung 181401046 Wesly S Sidabutar 181401127 .

OUTPUT PRIMITIF Output primitif adalah struktur dasar geometri yang paling sederhana dari gambar grafika komputer. Setiap output primitif mempunyai data koordinat dan informasi lain tentang bagaimana cara object ditampilkan pada layar. Titik dan garis lurus adalah bentuk geometri paling sederhana dan komponen gambar. e. .

OUTPUT PRIMITIF Setelah berhasil membangun output primitif, langkah selanjutnya adalah melakukan pengaturan terhadap atribut output primitif. Atribut adalah semua parameter yang mempengaruhi bagaimana primitive grafis ditampilkan. Atribut dari output primitif dapat berupa: Ukuran garis batas Tipe garis batas Warna objek (Fill color / Area Filling) e. .

ATRIBUT OUTPUT PRIMITIF Atribut dasar untuk titik adalah ukuran dan warna. Atribut dasar untuk garis adalah tipe (type), tebal (width) dan warna (color). e. .

MENGGAMBAR ELEMEN GEOMETRI Titik Garis Polyline Polygon e. .

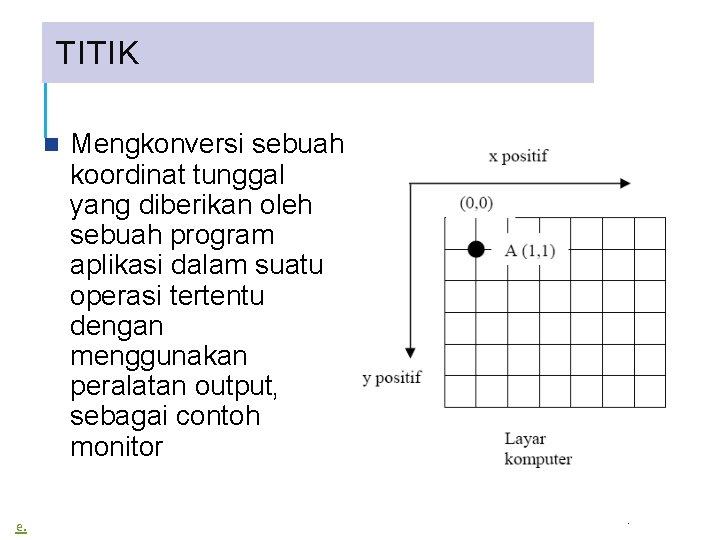
TITIK e. Mengkonversi sebuah koordinat tunggal yang diberikan oleh sebuah program aplikasi dalam suatu operasi tertentu dengan menggunakan peralatan output, sebagai contoh monitor.

GARIS e. Garis dibuat dengan menentukan posisi titik diantara titik awal dan akhir dari suatu garis, yaitu (x 1, y 1) dan (x 2, y 2). .

PIXEL unsur gambar atau representasi sebuah titik terkecil dalam sebuah gambar grafis. akronim bahasa Inggris Picture Element yang disingkat menjadi Pixel. Monitor ribuan piksel yang terbagi dalam baris-baris dan kolom-kolom. Jumlah piksel yang terdapat dalam sebuah monitor dapat kita ketahui dari resolusinya. Resolusi maksimum yang disediakan oleh monitor adalah 1024 x 768, maka jumlah pixel yang ada dalam layar monitor tersebut adalah 786432 piksel. Semakin tinggi jumlah piksel yang tersedia dalam monitor, semakin tajam gambar yang mampu ditampilkan oleh monitor tersebut. e. .

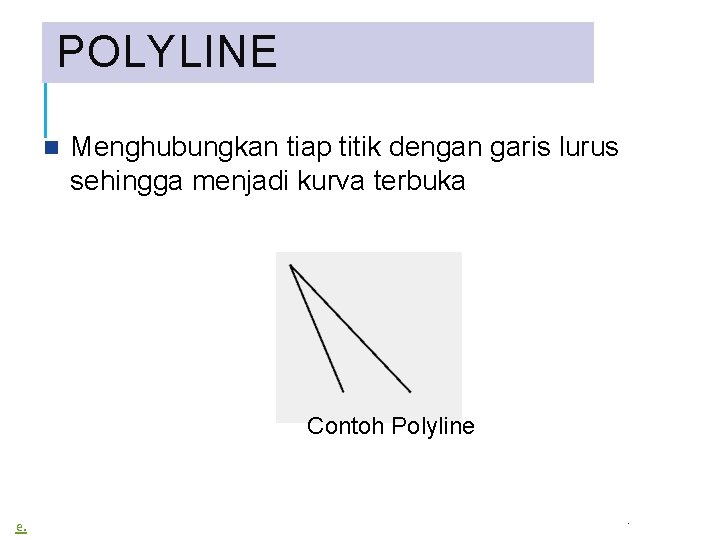
POLYLINE Menghubungkan tiap titik dengan garis lurus sehingga menjadi kurva terbuka Contoh Polyline e. .

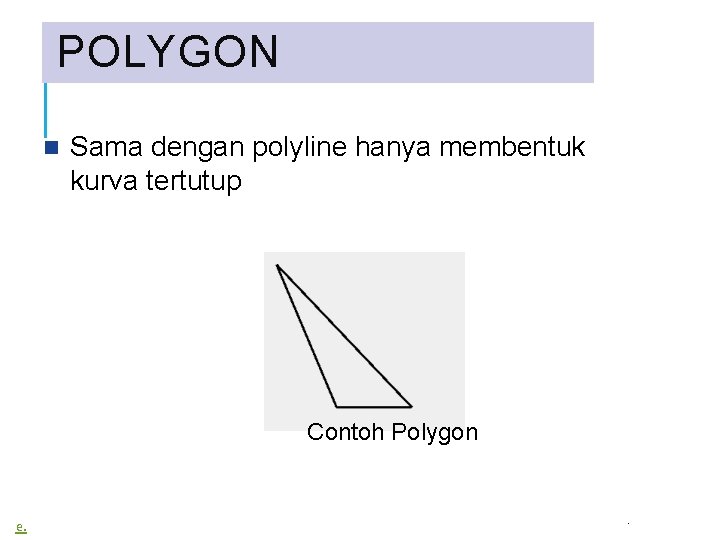
POLYGON Sama dengan polyline hanya membentuk kurva tertutup Contoh Polygon e. .

GARIS Dinyatakan dengan 4 nilai : x 1, y 1, x 2, y 2 Koordinat / titik awal (x 1, y 1) Koordinat / titik akhir (x 2, y 2) e. .

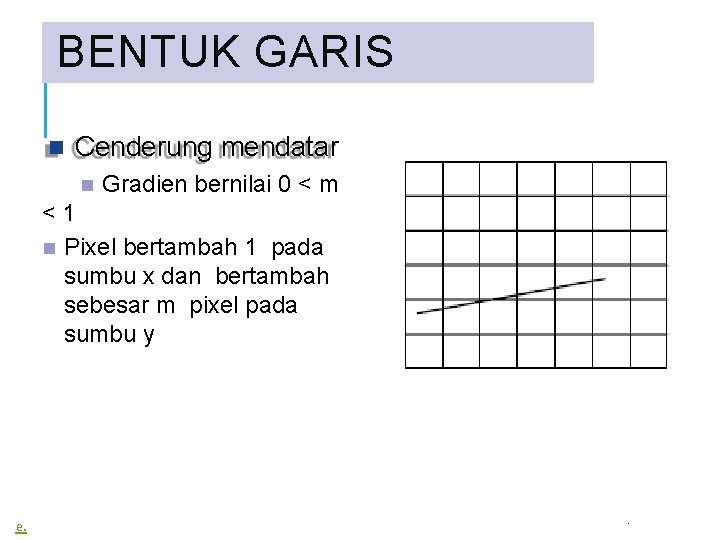
BENTUK GARIS Cenderung mendatar Gradien bernilai 0 < m <1 Pixel bertambah 1 pada sumbu x dan bertambah sebesar m pixel pada sumbu y e. .

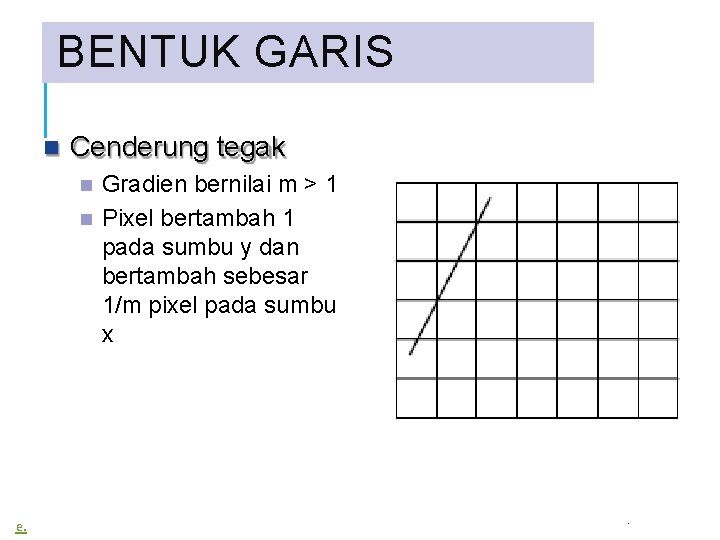
BENTUK GARIS Cenderung tegak Gradien bernilai m > 1 Pixel bertambah 1 pada sumbu y dan bertambah sebesar 1/m pixel pada sumbu x e. .

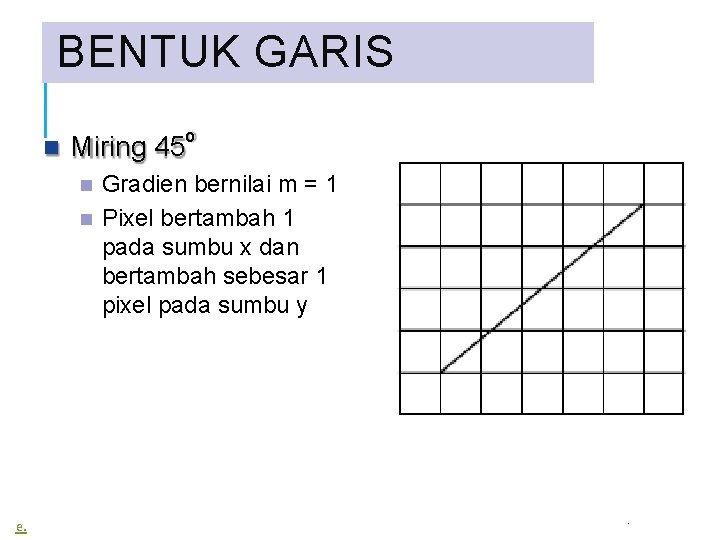
BENTUK GARIS Miring 45 o Gradien bernilai m = 1 Pixel bertambah 1 pada sumbu x dan bertambah sebesar 1 pixel pada sumbu y e. .

GRADIEN m = gradien / kemiringan garis Persamaan garis lurus : Y = mx + c M : gradien C : konstanta e. .

ALGORITMA DDA Algoritma Digital Differential Analyzer (DDA) adalah algoritma sederhana untuk menggambar garis Garis dikelompokkan ke dalam 3 bentuk : mendatar, cenderung tegak dan miring 45 derajat Nilai untuk gradien : m>1, m=1, 0<m<1 e. .

LANGKAH² ALGORITMA DDA Tentukan dua titik yang akan dihubungkan dalam pembentukan garis. 2. Tentukan salah satunya sebagai titik awal (x 1, y 1) dan yang lain sebagai titik akhir (x 2, y 2). 3. Hitung : dx = x 2 − x 1 dan dy = y 2 − y 1 4. Tentukan step, dengan ketentuan berikut: 1. bila |dx| > |dy|, maka step = |dx| bila tidak, maka step = |dy| 5. x_inc = dx / step y_inc = dy / step 6. Koordinat selanjutnya : x = x + x_inc y = y + y_inc 7. e. Hitung penambahan koordinat piksel dengan persamaan: 8. Lakukan pembulatan u = Round(x), v = Round(y), kemudian plot piksel (u, v) pada layar Ulangi point 6 dan 7 untuk menentukan posisi piksel berikutnya sampai x = x 2 dan y = y 2. .

ALGORITMA DDA Hasil dari fungsi : bilangan riil Koordinat pixel : integer Harus dibulatkan ke dalam integer terdekat e. .

CONTOH e. Diketahui 2 buah titik A(2, 1) dan titik B(8, 5) bila titik A sebagai titik awal dan titik B sebagai titik akhir, tentukan titik-titik antara yang menghubungkan titik A dan titik B sehingga membentuk garis AB dengan menggunakan algoritma DDA. .

CONTOH Titik awal (x 1, y 1) = A(2, 1) Titik akhir (x 2, y 2) = B(8, 5) dx = x 2 − x 1 = 8 − 2 = 6 dy = y 2 − y 1 = 5 − 1 = 4 Karena: |dx| > |dy|, maka step = |dx| = 6 x_inc = dx / step = 6/6 = 1 y_inc = dy / step = 4/6 = 0, 67 e. .

CONTOH Iterasi ke-1: (x, y) = (2, 1) x+x_inc = 2 + 1 = 3 y+y_inc = 1 + 0, 67 = 1, 67 Koordinat selanjutnya : (x, y) = (3; 1, 67) Pembulatan (3; 1, 67) ≈ (3, 2). Gambar titik (3, 2) dilayar ================== Iterasi ke-2: (x, y) = (3; 1, 67) x+x_inc = 3 + 1 = 4 y+y_inc = 1, 67 + 0, 67 = 2, 34 Koordinat selanjutnya : (x, y) = (4; 2, 34) Pembulatan (4; 2, 34) ≈ (4, 2). Gambar titik (4, 2) dilayar ================== Iterasi ke-3: (x, y) = (4; 2, 34) x. A+x_inc = 4 + 1 = 5 y. A+y_inc = 2, 34 + 0, 67= 3, 01 Koordinat selanjutnya : (x, y) = (5; 3, 01) Pembulatan (5; 3, 01) ≈ (5, 3). Gambar titik (5, 3) dilayar e. .

CONTOH Iterasi ke-4: (x, y) = (5; 3, 01) x. A+x_inc = 5 + 1 = 6 y. A+y_inc = 3, 01 + 0, 67 = 3, 68 Koordinat selanjutnya : (x, y) = (6; 3, 68) Pembulatan (6; 3, 68) ≈ (6, 4). Gambar titik (6, 4) dilayar =============== Iterasi ke-5: (x, y) = (6; 3, 68) x. A+x_inc = 6 + 1 = 7 y. A+y_inc = 3, 68 + 0, 67 = 4, 35 Koordinat selanjutnya : (x, y) = (7; 4, 35) Pembulatan (7; 4, 35) ≈ (7, 4). Gambar titik (7, 4) dilayar =============== e. ======= Iterasi ke-6: (x, y) = (7; 4, 35) x. A+x_inc = 7 + 1 = 8 y. A+y_inc = 4, 35 + 0, 67 = 5, 02 Koordinat selanjutnya : (x, y) = (8; 5, 02) .

CONTOH Karena x = x 2 = 8, y = y 2 = 5, maka iterasi dihentikan, sehingga diperoleh titik-titik pembentuk garis sebagai berikut: (2, 1), (3, 2), (4, 2), (5, 3), (6, 4), (7, 4) dan (8, 5). Bila digambar pada raster graphics diperoleh gambar: e. .

ALGORITMA BRESSENHAM Dikembangkan oleh Bresenham Berdasarkan selisih antara garis yang diinginkan terhadap setengah ukuran dari pixel yang sedang digunakan e. .

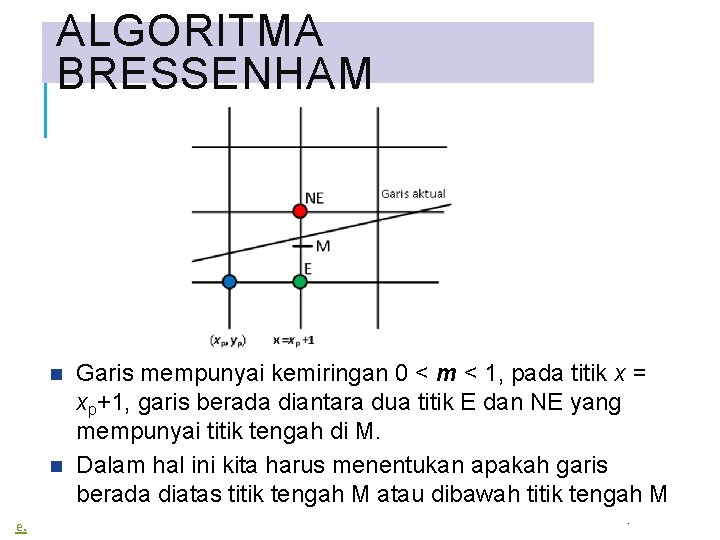
ALGORITMA BRESSENHAM Garis mempunyai kemiringan 0 < m < 1, pada titik x = xp+1, garis berada diantara dua titik E dan NE yang mempunyai titik tengah di M. Dalam hal ini kita harus menentukan apakah garis berada diatas titik tengah M atau dibawah titik tengah M e. .

LANGKAH² ALGORITMA BRESENHAM 5. Notes: algoritma midpoint Bresenham (untuk kemiringan 0 < m < 1) 1. Tentukan dua titik yang akan dihubungkan dalam pembentukan garis. 2. Tentukan salah satu sebagai titik awal (x 0, y 0) dan titik akhir (x 1, y 1). 3. Hitung dx, dy, 2 dx, 2 dy dan 2 dy − 2 dx 4. Hitung parameter: po = 2 dy − dx e. Untuk setiap xk sepanjang jalur garis, dimulai dengan k=0 bila pk < 0 maka titik selanjutnya adalah: (xk+1, yk) dan pk+1 = pk + 2 dy bila tidak, titik selanjutnya adalah (xk+1, yk+1) dan pk+1 = pk + 2 dy – 2 dx 7. Ulangi nomor 5 untuk menentukan posisi piksel berikutnya, sampai x = x 1 dan y = y 1 .

CONTOH e. Diketahui 2 buah titik A(2, 1) dan titik B(8, 5) bila titik A sebagai titik awal dan titik B sebagai titik akhir, tentukan titik-titik antara yang menghubungkan titik A dan titik B sehingga membentuk garis AB dengan menggunakan algoritma Bressenham. .

CONTOH e. Titik awal (x 0, y 0) = A(2, 1) Titik akhir (x 1, y 1) = B(8, 5) dx = x 1 − x 0 = 8 − 2 = 6 dy = y 1 − y 0 = 5 − 1 = 4 2. dx = 2. 6 = 12 2. dy = 2. 4 = 8 2 dy − 2 dx = 8 − 12 = − 4 po = 2. dy − dx = 8 − 6 = 2.

CONTOH e. Iterasi ke-1 (k = 0): Titik awal = (2, 1) Po = 2 > 0, maka titik selanjutnya adalah x = 2 + 1 = 3 dan y = 1 + 1 = 2, koordinat selanjutnya: (3, 2) p 1 = p 0 + 2 dy – 2 dx = 2 − 4 = − 2 ================== Iterasi ke-2 ( k = 1): Titik awal = (3, 2) P 1 = − 2 < 0, maka titik selanjutnya adalah x = 3 + 1 = 4 dan y = 2, koordinat selanjutnya : (4, 2) p 2 = p 1 + 2 dy = − 2 + 8 = 6 ================== Iterasi ke-3: (k=2) Titik awal = (4, 2) P 2 = 6 > 0, maka titik selanjutnya adalah x = 4 + 1 = 5 dan y = 2 + 1 = 3, koordinat selanjutnya : (5, 3) p 3 = p 2 + 2 dy – 2 dx = 6 − 4 = 2.

CONTOH e. Iterasi ke-4: (k=3) Titik awal = (5, 3) P 3 = 2 > 0, maka titik selanjutnya adalah x = 5 + 1 = 6 dan y = 3 + 1 = 4, koordinat selanjutnya : (6, 4) p 4 = p 3 + 2 dy – 2 dx = 2 − 4 = − 2 ================== Iterasi ke-5: (k=4) Titik awal = (6, 4) P 3 = − 2 < 0, maka titik selanjutnya adalah x = 6 + 1 = 7 dan y = 4, koordinat selanjutnya : (7, 4) p 5 = p 4 + 2 dy = − 2 + 8 = 6 ================== Iterasi ke-6: (k=5) Titik awal = (7, 4) P 5 = 6 > 0, maka titik selanjutnya adalah x = 7 + 1 = 8 dan y = 4 + 1 = 5, koordinat selanjutnya : (8, 5) .

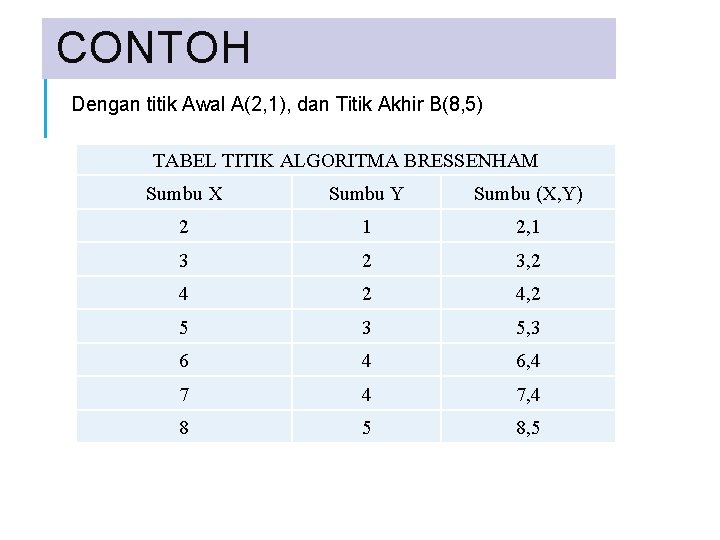
CONTOH Dengan titik Awal A(2, 1), dan Titik Akhir B(8, 5) TABEL TITIK ALGORITMA BRESSENHAM Sumbu X Sumbu Y Sumbu (X, Y) 2 1 2, 1 3 2 3, 2 4, 2 5 3 5, 3 6 4 6, 4 7, 4 8 5 8, 5

CONTOH Karena x = x 1 = 8, y = y 1 = 5, maka iterasi dihentikan, sehingga diperoleh titik-titik pembentuk garis sebagai berikut: (2, 1), (3, 2), (4, 2), (5, 3), (6, 4), (7, 4) dan (8, 5). Bila digambar pada raster graphics diperoleh gambar: e. .

NOTES! Untuk kemiringan − 1 < m < 0 , kita tinggal mengganti komponen berikut: Untuk setiap xk sepanjang jalur garis, dimulai dengan k=0 bila pk < 0 maka titik selanjutnya adalah: (xk+1, yk) dan pk+1 = pk + 2 dy bila tidak, titik selanjutnya adalah: (xk+1, yk− 1) dan pk+1 = pk + 2 dy – 2 dx e. .

NOTES! Notes: Untuk kemiringan m > 1) dua titik yang akan dihubungkan dalam pembentukan garis. 2. Tentukan salah satu sebagai titik awal (x 0, y 0) dan titik akhir (x , y ). 1 3. Hitung dx, dy, 2 dx, 2 dy dan 2 dx − 2 dy 4. Hitung parameter: po = 2 dx − dy 5. bila pk < 0 maka titik selanjutnya adalah: (xk, yk+1) dan pk+1 = pk + 2 dx bila tidak, titik selanjutnya adalah (xk+1, yk+1) dan pk+1 = pk + 2 dx – 2 dy 1. Tentukan e. Untuk setiap yk sepanjang jalur garis, dimulai dengan k=0 1 7. Ulangi nomor 5 untuk menentukan posisi piksel berikutnya, sampai x = x 1 dan y = y 1 .

Lingkaran ALGORITMA e. PEMBENTUK Simetris Delapan Titik Pembuatan kurva lingkaran dapat dilakukan dengan menentukan titik awal (x, y) yang terletak pada lingkaran, maka tujuh titik yang lain (yang terletak pada lingkaran juga) dapat ditentukan sebagai berikut: (−x, y), (x, −y), (−x, −y), (y, x), (−y, x), (y, −x), (−y, −x) .

Lingkaran ALGORITMA PEMBENTUK Algoritma Midpoint Algoritma midpoint juga disebut algoritma lingkaran Bressenham Pembentukan semua titik berdasarkan titik pusat dengan penambahan semua jalur di sekelilingkaran e. Garis lingkaran berada diantara titik (xk+1, yk) dan (xk+1, yk − 1) .

LANGKAH² ALGORITMA MIDPOINT 1. 2. Tentukan jari-jari r dan pusat lingkaran (xp, yp), kemudian setting sedemikian rupa sehingga titik awal berada pada: (x 0, y 0) = (0 , r) Hitung nilai parameter: p 0= 5/4 –r -> Jika jari-jari r pecahan p 0= 1 –r -> Jika jari-jari r bulat 3. Untuk setiap posisi xk, dimulai dengan k = 0: bila tidak, titik selanjutnya adalah: (xk+1, yk - 1) dan pk+1 = pk + 2 xk+1 + 1 – 2 yk+1 4. Tentukan titik simetris pada ketujuh oktan yang lain 5. Gerakkan setiap posisi piksel (x, y) pada garis lingkaran dengan titik pusat (xp, yp) dan plot nilai koordinat: x = x + x p; y=y+ yp 6. Ulangi langkah 3 sampai dengan 5 hingga x ≥ y bila pk < 0 maka titik selanjutnya adalah: (xk+1, yk) dan pk+1 = pk + 2 xk+1 + 1 e. .

CONTOH e. Buatlah gambar kurva lingkaran dengan pusat lingkaran (0, 0) dan jari-jari 8, perhitungan berdasarkan dari oktan kuadran pertama dimana x = 0 sampai x = y. Koordinat titik awal dimulai dari (x, r) = (0, 8). Karena jari-jari r bulat, maka gunakan p 0 = 1 – r. .

CONTOH Iterasi ke-1 (k = 0; x 0 = 0; y 0 = r = 8; p 0 = 1 – r = 1 – 8 = -7) Karena p 0 < 0, maka : x 1 = x 0 + 1 = 1 dan y 1 = y 0 = 8; jadi titik selanjutnya: (1, 8) p 1 = p 0 + 2 x 1 + 1 = – 7 + 2. (1) + 1 = – 4 Dengan algoritma simetris delapan titik, maka diperoleh titik-titik berikut : (1, 8), (– 1, 8), (1, – 8), (– 1, – 8), (8, 1), (– 8, 1), (8, – 1), (– 8, – 1) ================== Iterasi ke-2 (k = 1; x 1 = 1; y 1 = 8; p 1 = -4) Karena p 1 < 0, maka : x 2 = x 1 + 1 = 2 dan y 2 = y 1 = 8; jadi titik selanjutnya: (2, 8) p 2 = p 1 + 2 x 2 + 1 = – 4 + 2. (2) + 1 = 1 Dengan algoritma simetris delapan titik, maka diperoleh titik-titik berikut : (2, 8), (– 2, 8), (2, – 8), (– 2, – 8), (8, 2), (– 8, 2), (8, – 2), (– 8, – 2) ================== e. .

CONTOH e. Iterasi ke-3 (k = 2; x 3 = 2; y 3 = 8; p 3 = 1) Karena p 2 > 0, maka jadi Titik selanjutnya : (3, 7) x 3 = x 2 + 1 = 3 dan y 3 = y 2 – 1 = 8 – 1 = 7 , p 3 = p 2 + 2 x 3 + 1 – 2 y 3 = 1 + 2. (3) + 1 – 2. (7) = – 6 Dengan algoritma simetris delapan titik, maka diperoleh titik-titik berikut : (3, 7), (– 3, 7), (3, – 7), (– 3, – 7), (7, 3), (– 7, 3), (7, – 3), (– 7, – 3) ================== Iterasi ke-4 (k = 3; x 1 = 3; y 1 = 7; p 1 = -6) Karena p 3 < 0, maka x 4 = x 3 + 1 = 4 dan y 4 = y 3 = 7, jadi Titik selanjutnya : (4, 7) p 4 = p 3 + 2 x 4 + 1 = – 6 + 2. (4) + 1 = 3 Dengan algoritma simetris delapan titik, maka diperoleh titik-titik berikut : (4, 7), (– 4, 7), (4, – 7), (– 4, – 7), (7, 4), (– 7, 4), (7, – 4), (– 7, – 4) ================== .

CONTOH Iterasi ke-5 (k = 4; x 3 = 4; y 3 = 7; p 3 = 3) Karena p 4 > 0, maka x 5 = x 4 + 1 = 5 dan y 5 = y 4 – 1 = 7 – 1 = 6 , jadi Titik selanjutnya : (5, 6) p 5 = p 4 + 2 x 4 + 1 – 2 y 4 = 3 + 2. (5) + 1 – 2. (6) = 2 Dengan algoritma simetris delapan titik, maka diperoleh titik berikut : (5, 6), (– 5, 6), (5, – 6), (– 5, – 6), (6, 5), (– 6, 5), (6, – 5), (– 6, – 5) ================== Iterasi ke-6 (k = 5; x 1 = 5; y 1 = 6; p 1 = 2) Karena p 5 > 0, maka x 6 = x 5 + 1 = 6 dan y 6 = y 5 – 1 = 6 – 1 = 5 , jadi Titik selanjutnya : (6, 5) Iterasi dihentikan karena X > Y. e. .

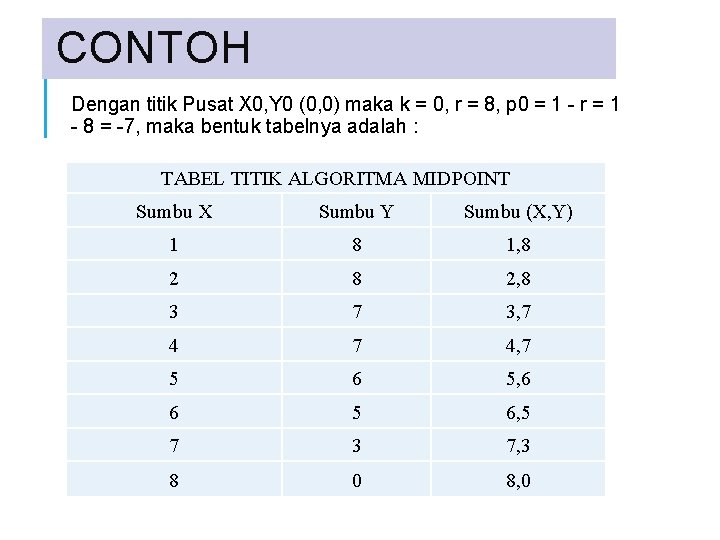
CONTOH Dengan titik Pusat X 0, Y 0 (0, 0) maka k = 0, r = 8, p 0 = 1 - r = 1 - 8 = -7, maka bentuk tabelnya adalah : TABEL TITIK ALGORITMA MIDPOINT Sumbu X Sumbu Y Sumbu (X, Y) 1 8 1, 8 2, 8 3 7 3, 7 4, 7 5 6 5, 6 6 5 6, 5 7 3 7, 3 8 0 8, 0

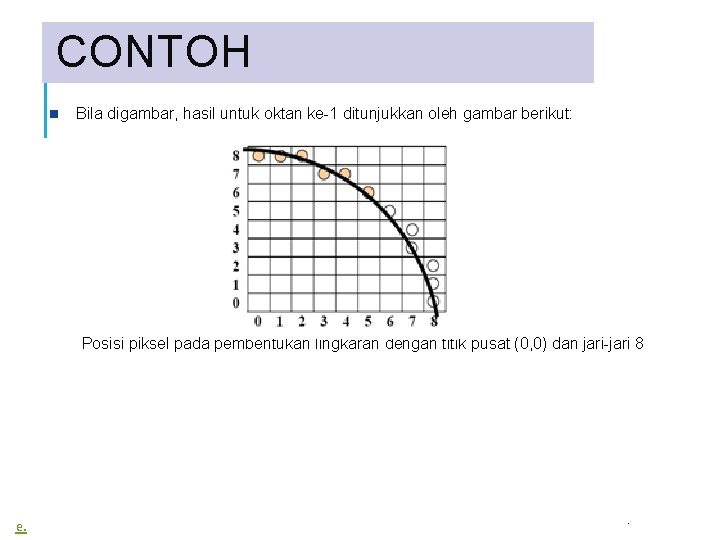
CONTOH Bila digambar, hasil untuk oktan ke-1 ditunjukkan oleh gambar berikut: Posisi piksel pada pembentukan lingkaran dengan titik pusat (0, 0) dan jari-jari 8 e. .