Cellular Automata Various credits for these slides Ajit

Cellular Automata Various credits for these slides: Ajit Narayanan, Rod Hunt, several more.

Cellular Automata A CA is a spatial lattice of N cells, each of which is one of k states at time t. • Each cell follows the same simple rule for updating its state. • The cell's state s at time t+1 depends on its own state and the states of some number of neighbouring cells at t. • For one-dimensional CAs, the neighbourhood of a cell consists of the cell itself and r neighbours on either side. Hence, k and r are the parameters of the CA. • CAs are often described as discrete dynamical systems with the capability to model various kinds of natural discrete or continuous dynamical systems

Example of 1 -D cellular automaton • For a binary input N long, are there more 1 s than 0 s? • Set k=2 and r=1 with the following rule: Cell + 2 neighbours: Result: 000 001 010 011 100 101 110 111 0 0 0 1 1 1 That is, the value of a cell at time t+1 will depend on its value and the values of its two immediate neighbours at time t. This is a form of ‘majority voting’ between all three cells.

Density classification • In the above example, we have assumed wrap-around, and r=1. • In this case, the CA has reached a ‘limit point’ from which no escape is possible. • CAs have been used for simulating fluid dynamics, chemical oscillations, crystal growth, galaxy formation, stellar accretion disks, fractal patterns on mollusc shells, parallel formal language recognition, plant growth, traffic flow, urban segregation, image processing tasks, etc …

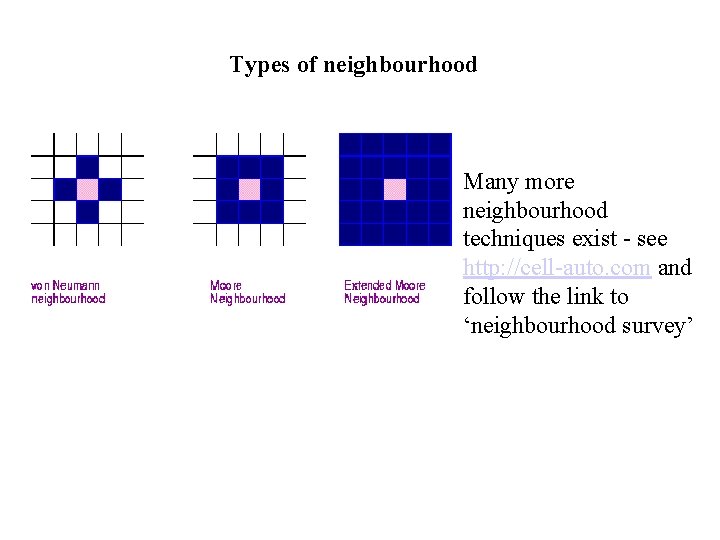
Types of neighbourhood Many more neighbourhood techniques exist - see http: //cell-auto. com and follow the link to ‘neighbourhood survey’

Classes of cellular automata (Wolfram) Class 1: after a finite number of time steps, the CA tends to achieve a unique state from nearly all possible starting conditions (limit points) Class 2: the CA creates patterns that repeat periodically or are stable (limit cycles) – probably equivalent to a regular grammar/finite state automaton Class 3: from nearly all starting conditions, the CA leads to aperiodic-chaotic patterns, where the statistical properties of these patterns are almost identical (after a sufficient period of time) to the starting patterns (self-similar fractal curves) – computes ‘irregular problems’ Class 4: after a finite number of steps, the CA usually dies, but there a few stable (periodic) patterns possible (e. g. Game of Life) - Class 4 CA are believed to be capable of universal computation

John Conway’s Game of Life • 2 D cellular automata system. • Each cell has 8 neighbors - 4 adjacent orthogonally, 4 adjacent diagonally. This is called the Moore Neighborhood.

Simple rules, executed at each time step: – A live cell with 2 or 3 live neighbors survives to the next round. – A live cell with 4 or more neighbors dies of overpopulation. – A live cell with 1 or 0 neighbors dies of isolation. – An empty cell with exactly 3 neighbors becomes a live cell in the next round.

Is it alive? • http: //www. bitstorm. org/gameoflife/ • Compare it to the definitions…

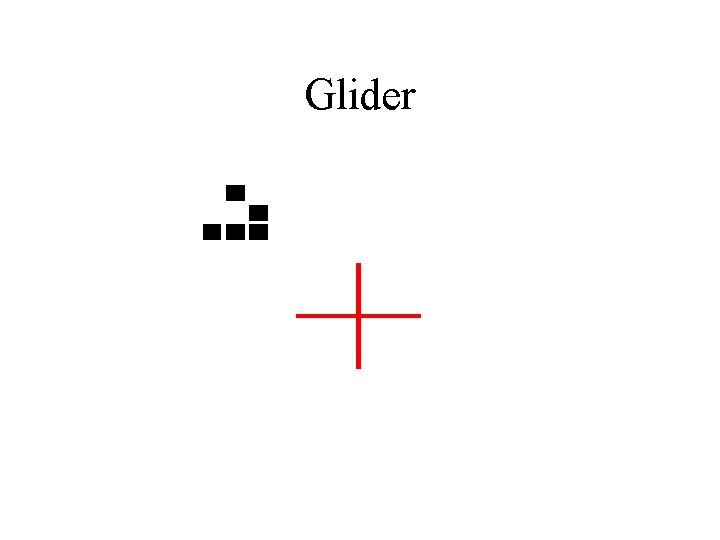
Glider

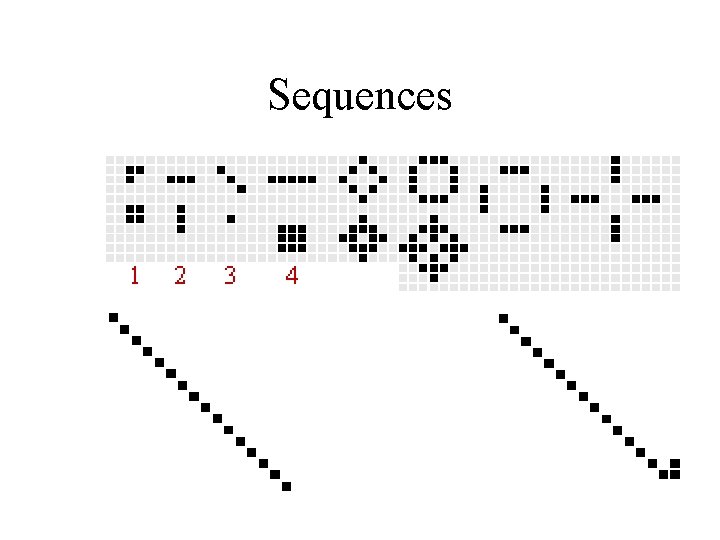
Sequences

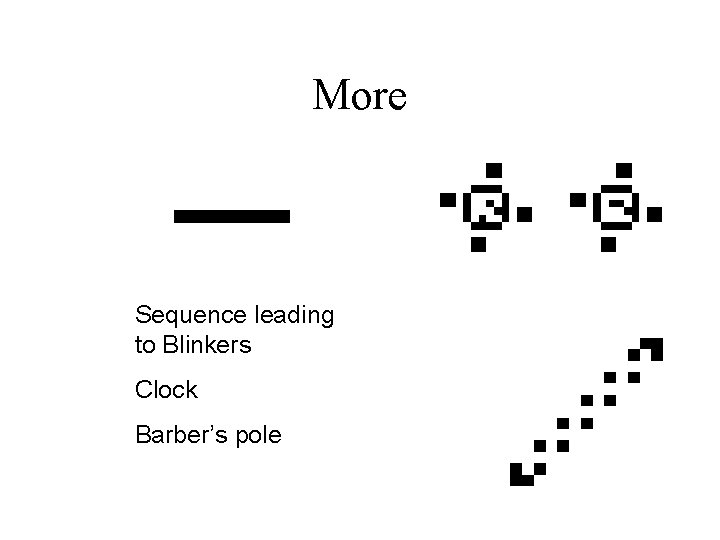
More Sequence leading to Blinkers Clock Barber’s pole

A Glider Gun

Loops • Assumptions – Computation universality not required • Characteristics – – – 8 states, 2 D Cellular automata Needed CA grid of 100 cells Self Reproduction into identical copy Input tape with data and instructions Concept of Death • Significance – Could be modeled through computer programs

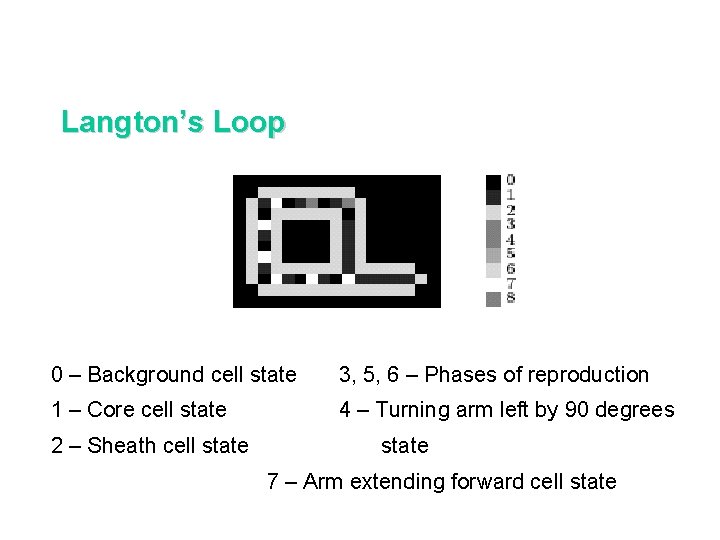
Langton’s Loop 0 – Background cell state 3, 5, 6 – Phases of reproduction 1 – Core cell state 4 – Turning arm left by 90 degrees 2 – Sheath cell state 7 – Arm extending forward cell state

Loop Reproduction

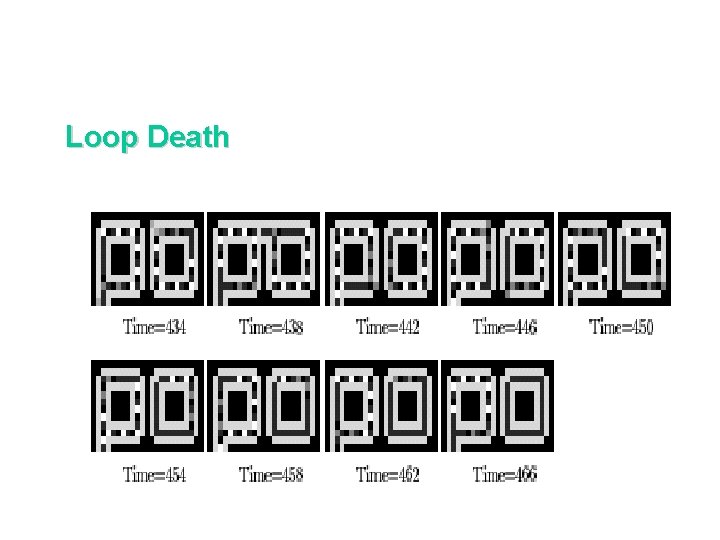
Loop Death

Langton’s Loops Chris Langton formulated a much simpler form of self-rep structure - Langton's loops - with only a few different states, and only small starting structures.

Example: Modelling Sharks and Fish: Predator/Prey Relationships Bill Madden, Nancy Ricca and Jonathan Rizzo Graduate Students, Computer Science Department Research Project using Department’s 20 -CPU Cluster

• This project modeled a predator/prey relationship • Begins with a randomly distributed population of fish, sharks, and empty cells in a 1000 x 2000 cell grid (2 million cells) • Initially, – 50% of the cells are occupied by fish – 25% are occupied by sharks – 25% are empty

Here’s the number 2 million • Fish: red; sharks: yellow; empty: black

Rules A dozen or so rules describe life in each cell: • birth, longevity and death of a fish or shark • breeding of fish and sharks • over- and under-population • fish/shark interaction • Important: what happens in each cell is determined only by rules that apply locally, yet which often yield long-term large-scale patterns.

Do a LOT of computation! • • • Apply a dozen rules to each cell Do this for 2 million cells in the grid Do this for 20, 000 generations Well over a trillion calculations per run! Do this as quickly as you can

Do a LOT of computation! • We used a 20 -CPU cluster in the Computer Science Department (Galaxy) • ‘Gal’ is the smaller of two clusters run by the Department (larger one has 64 CPUs) • 15 x faster than a single PC • Longest runs still took about 45 minutes • GO PARALLEL !!!

Rules in detail: Initial Conditions Initially cells contain fish, sharks or are empty • Empty cells = 0 (black pixel) • Fish = 1 (red pixel) • Sharks = – 1 (yellow pixel)

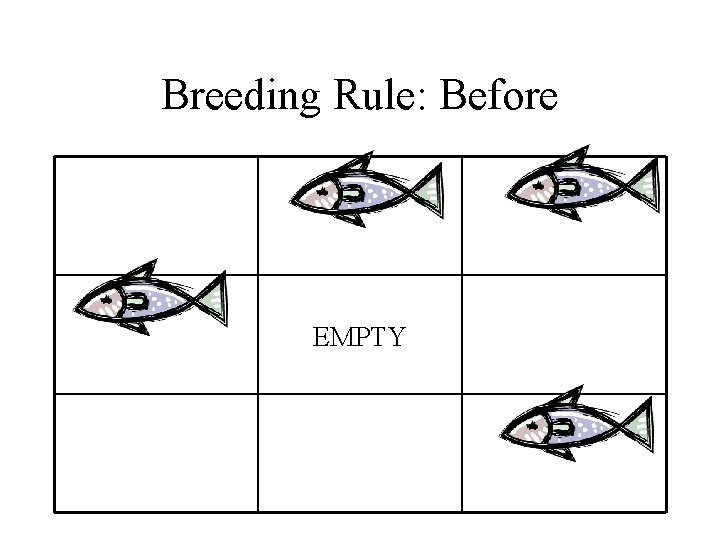
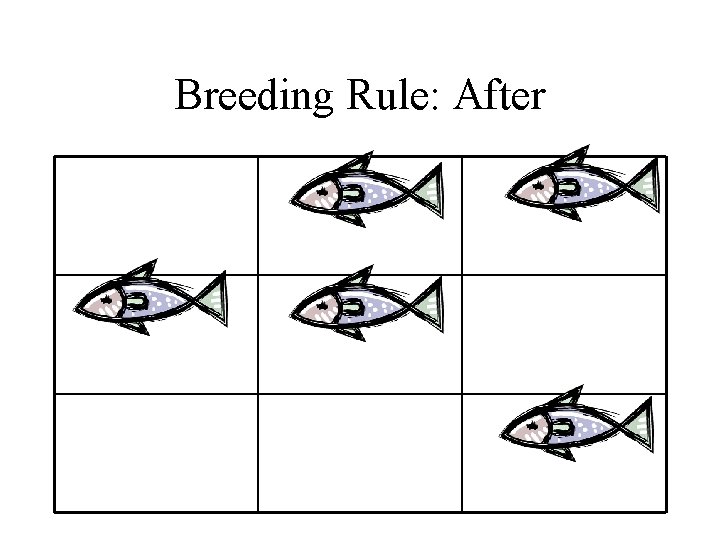
Rules in detail: Breeding Rule Breeding rule: if the current cell is empty • If there are >= 4 neighbors of one species, and >= 3 of them are of breeding age, » Fish breeding age >= 2, » Shark breeding age >=3, and there are <4 of the other species: then create a species of that type » +1= baby fish (age = 1 at birth) » -1 = baby shark (age = |-1| at birth)

Breeding Rule: Before EMPTY

Breeding Rule: After

Rules in Detail: Fish Rules If the current cell contains a fish: • Fish live for 10 generations • If >=5 neighbors are sharks, fish dies (shark food) • If all 8 neighbors are fish, fish dies (overpopulation) • If a fish does not die, increment age

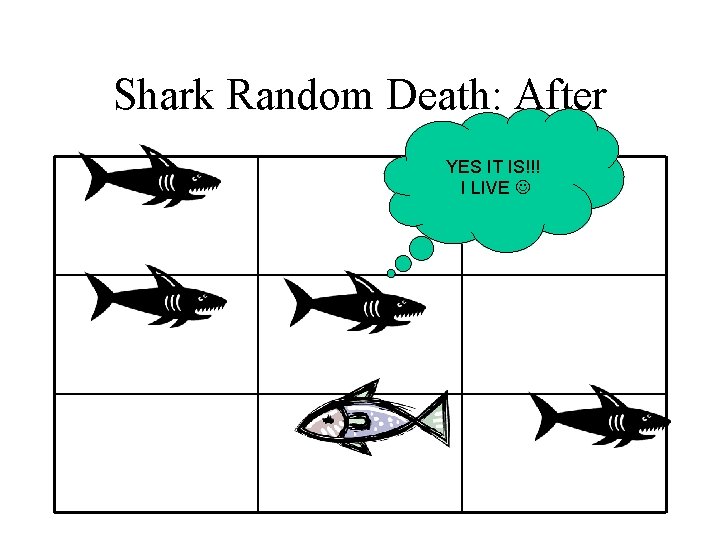
Rules in Detail: Shark Rules If the current cell contains a shark: • Sharks live for 20 generations • If >=6 neighbors are sharks and fish neighbors =0, the shark dies (starvation) • A shark has a 1/32 (. 031) chance of dying due to random causes • If a shark does not die, increment age

Shark Random Death: Before I Sure Hope that the random number chosen is >. 031

Shark Random Death: After YES IT IS!!! I LIVE

Sample Code (C++): Breeding Spring 2005 JR 33

Results • Next several screens show behavior over a span of 10, 000+ generations

Generation: 0 Spring 2005 BM 35

Generation: 100 Spring 2005 BM 36

Generation: 500

Generation: 1, 000

Generation: 2, 000

Generation: 4, 000

Generation: 8, 000

Generation: 10, 500

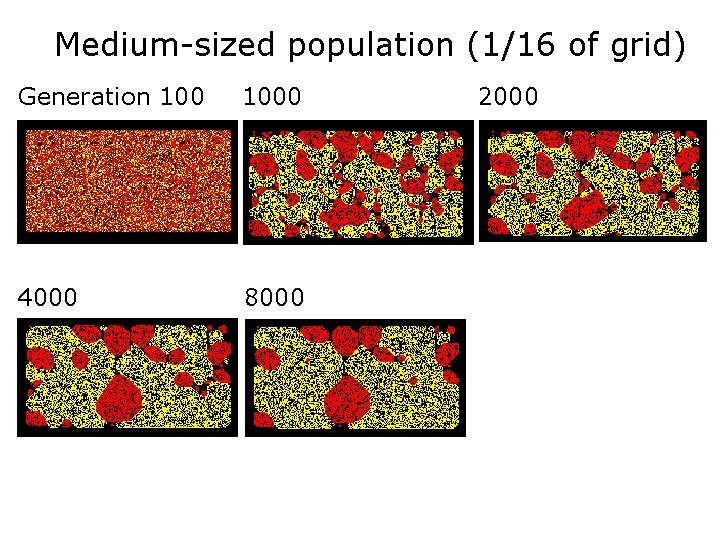
Long-term trends • Borders tended to ‘harden’ along vertical, horizontal and diagonal lines • Borders of empty cells form between like species • Clumps of fish tend to coalesce and form convex shapes or ‘communities’

Variations of Initial Conditions • Still using randomly distributed populations: – Medium-sized population. Fish/sharks occupy: 1/16 th of total grid Fish: 62, 703; Sharks: 31, 301 – Very small population. Fish/sharks occupy: 1/800 th of total grid Initial population: Fish: 1, 298; Sharks: 609

Medium-sized population (1/16 of grid) Generation 1000 4000 8000 2000

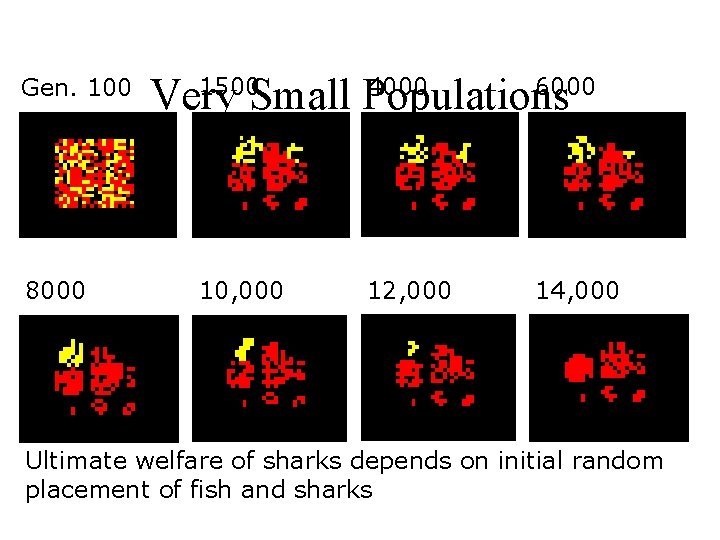
Very Small Populations • Random placement of very small populations can favor one species over another • Fish favored: sharks die out • Sharks favored: sharks predominate, but fish survive in stable small numbers

Gen. 100 8000 Very Small Populations 1500 4000 6000 10, 000 12, 000 14, 000 Ultimate welfare of sharks depends on initial random placement of fish and sharks

Very small populations • Fish can live in stable isolated communities as small as 20 -30 • A community of less than 200 sharks tends not to be viable

This is what a community of virtual plants looks like Community image Contrasting tones show patches of resource

CSRThis type, frame 1 is a single propagule of a virtual plant It is about to grow in a resource-rich aboveand below-ground environment

ditto f. 2

ditto f. 3

ditto f. 4

ditto f. 5

ditto f. 6

ditto f. 7

ditto f. 8

ditto f. 9

ditto f. 10

ditto f. 11

ditto f. 12

ditto f. 13

ditto f. 14

ditto f. 15

ditto f. 16

ditto f. 17

ditto f. 18

ditto f. 19

ditto 20 The plant hasf. produced abundant growth aboveand below-ground and zones of resource depletion have appeared

See Rod Hunt at http: //www. ex. ac. uk/~rh 203/ for lots more about the plant life CA and its uses