6 3 Trig Equations Involving Multiple Angles 6



















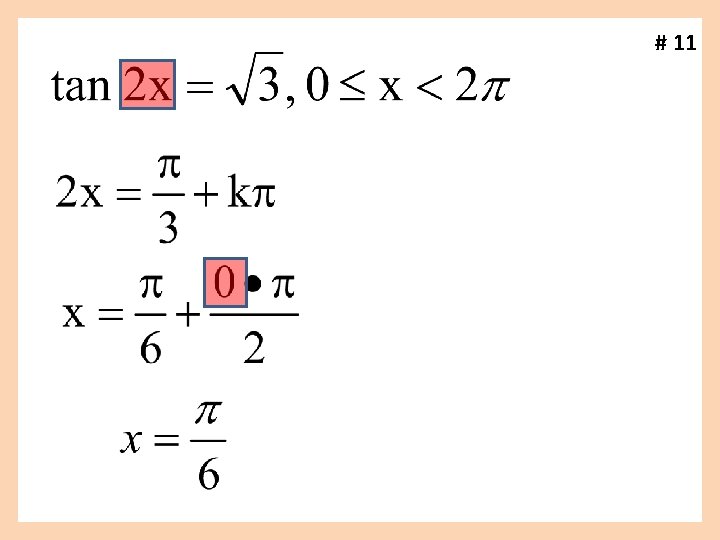


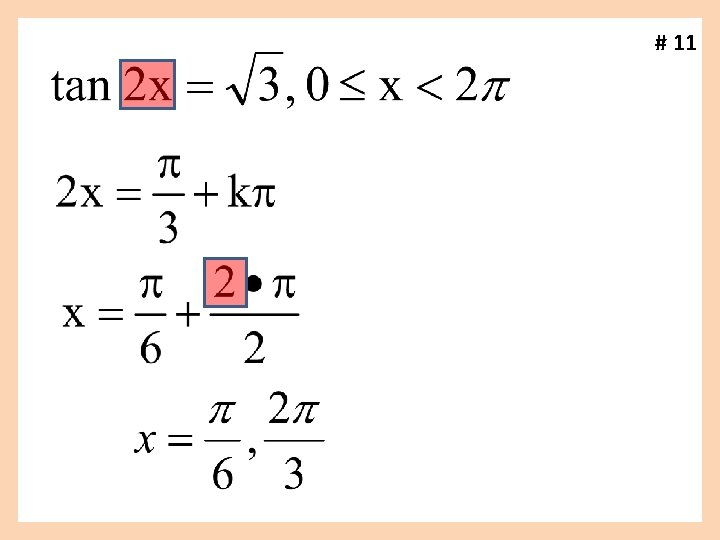
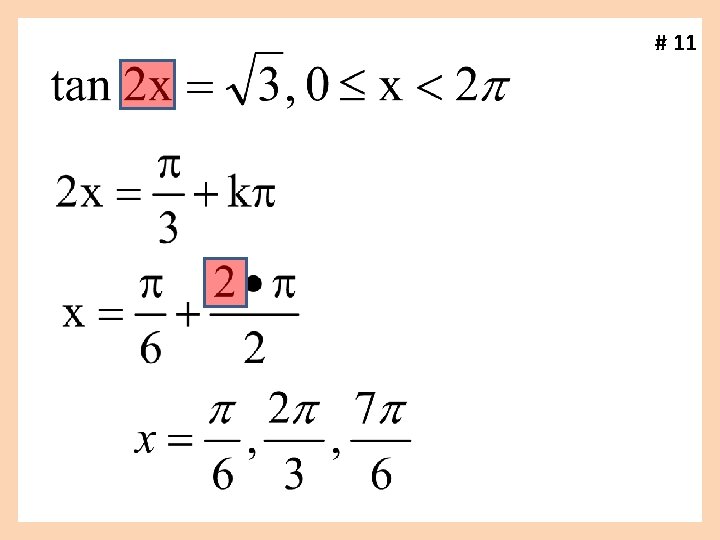
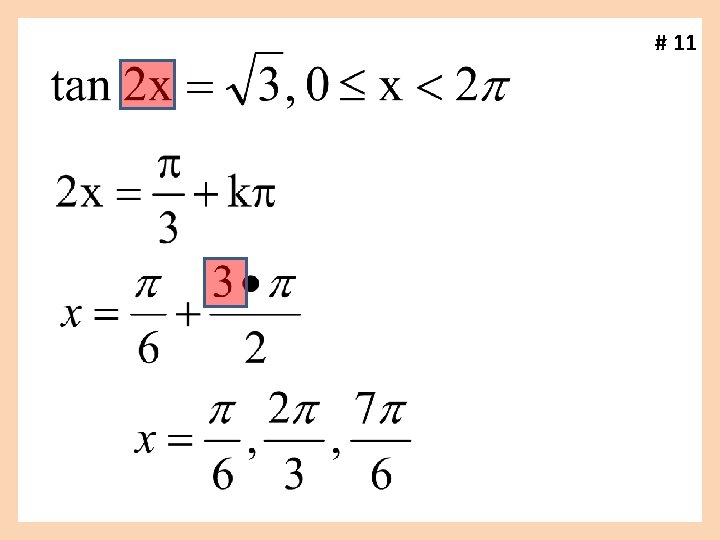
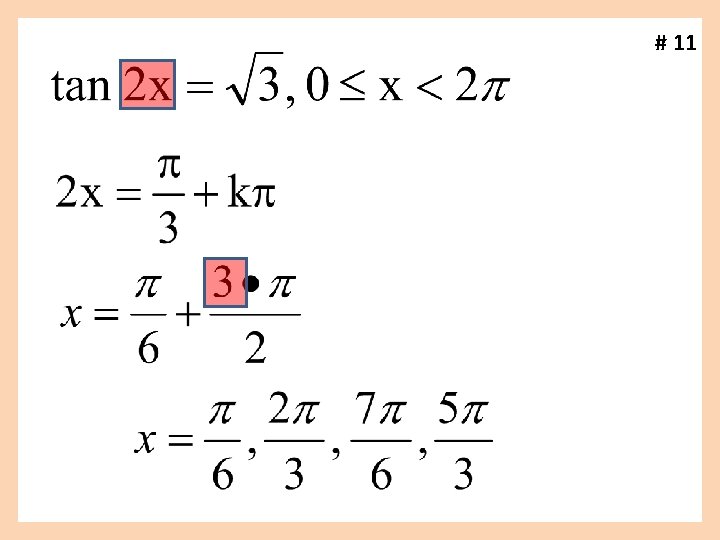


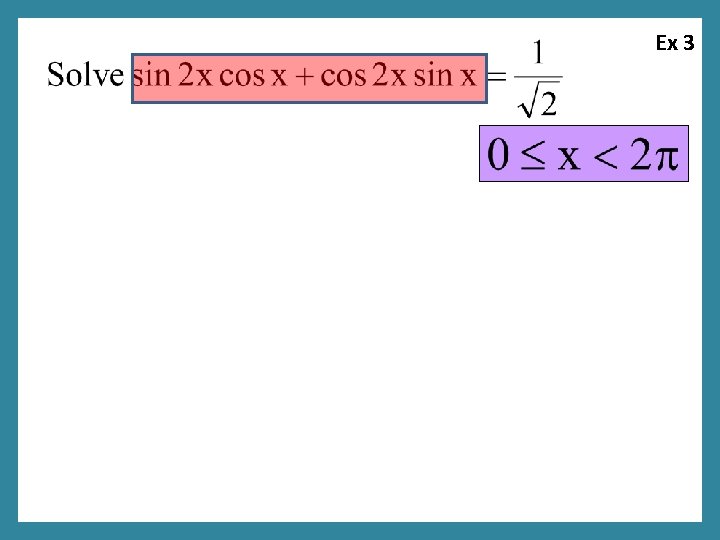



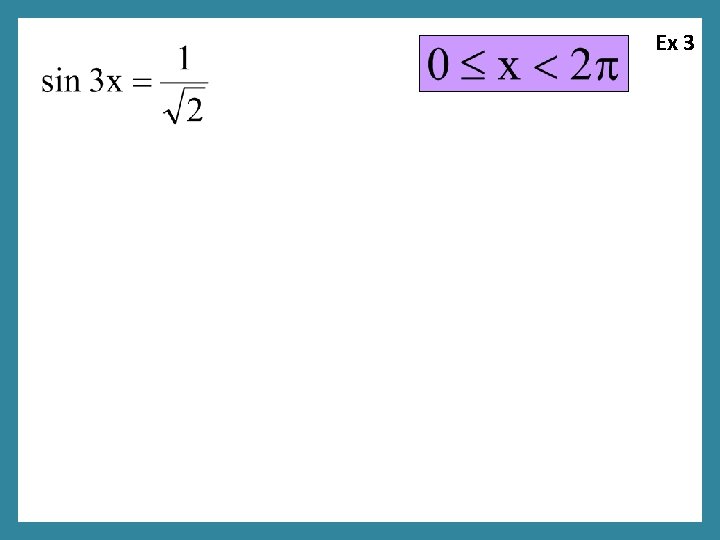
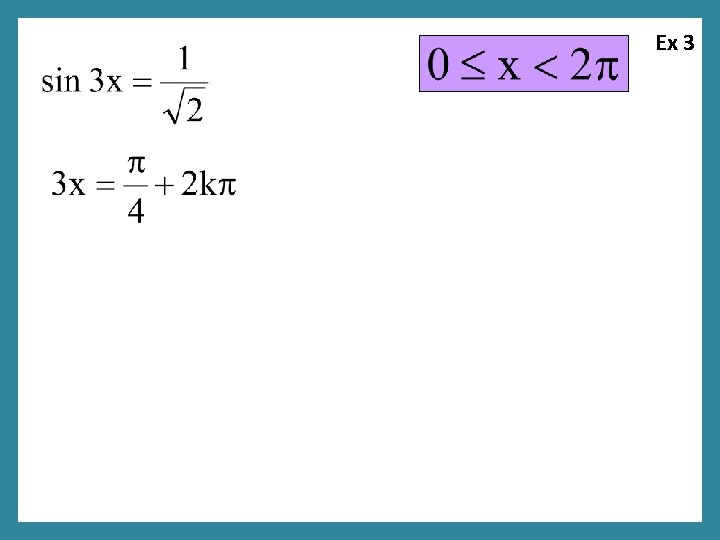
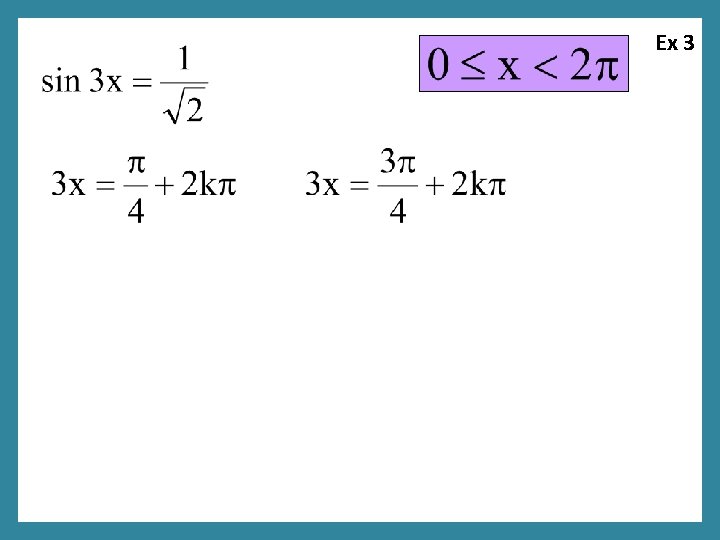
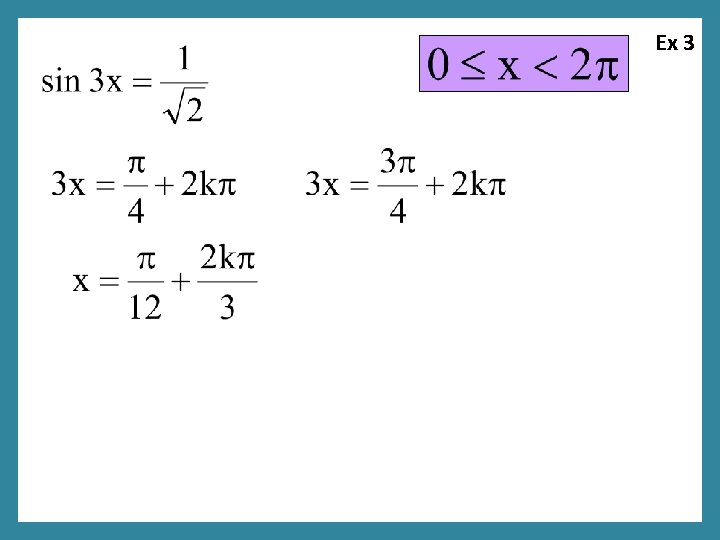
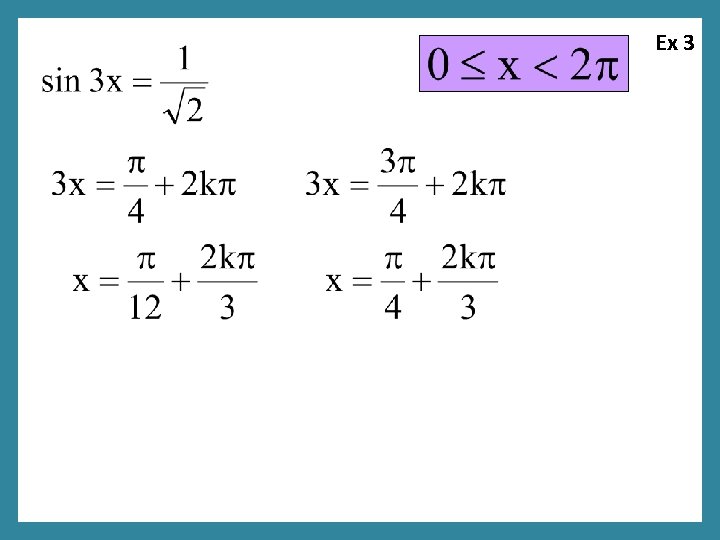




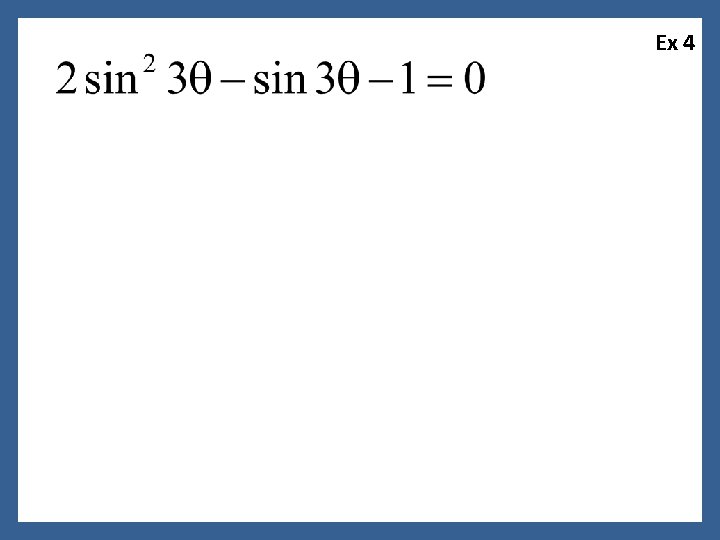



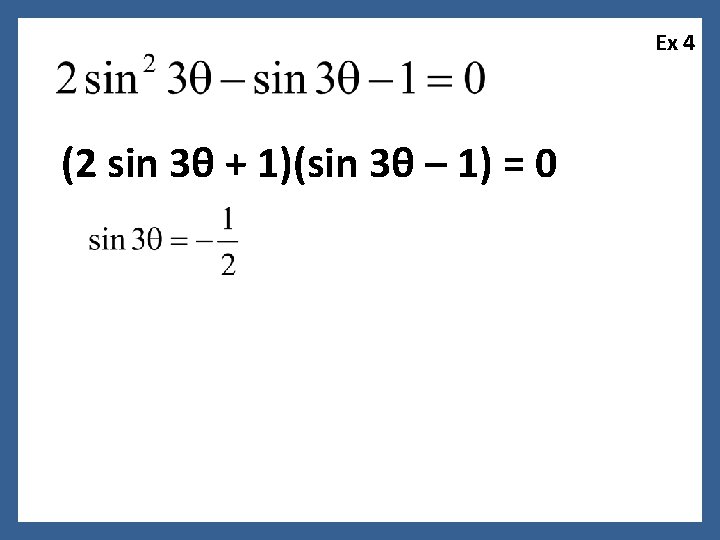
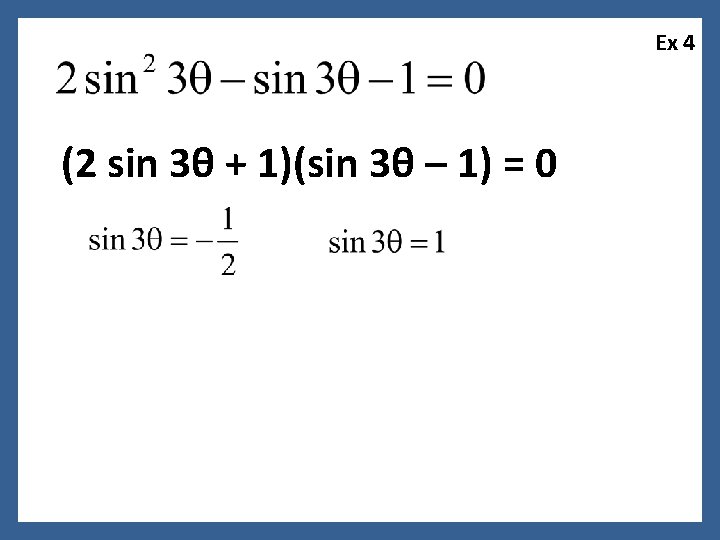








































- Slides: 95

6. 3 Trig Equations Involving Multiple Angles

6. 3 Trig Equations Involving Multiple Angles If you tackle a trig equation with 2θ or 3θ, that enters into your calculations. . . and you get more answers.

6. 3 Trig Equations Involving Multiple Angles • Addition / Multiplication Property • Factoring • Quadratic equations • Square both sides (E. S. )

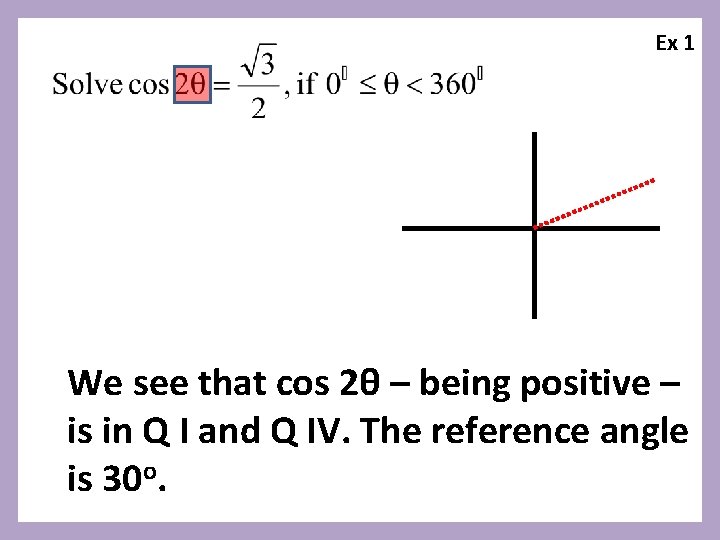
Ex 1

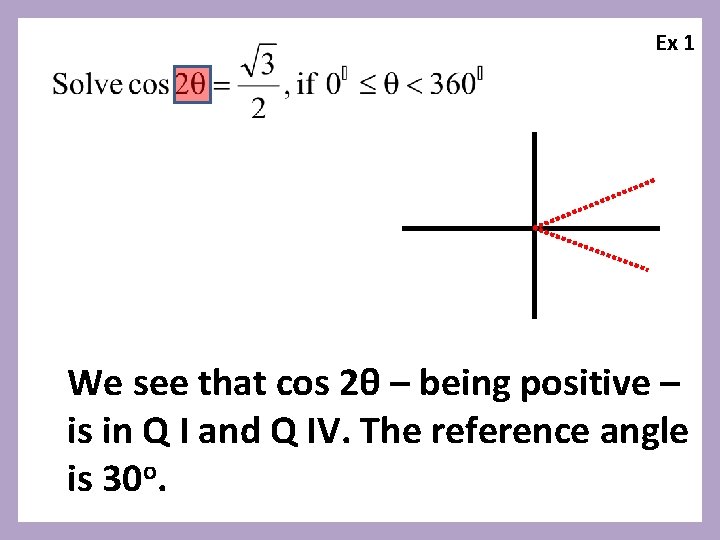
Ex 1 We see that cos 2θ – being positive – is in Q I and Q IV.

Ex 1 We see that cos 2θ – being positive – is in Q I and Q IV. The reference angle is 30 o.

Ex 1 We see that cos 2θ – being positive – is in Q I and Q IV. The reference angle is 30 o.

Ex 1 We see that cos 2θ – being positive – is in Q I and Q IV. The reference angle is 30 o.

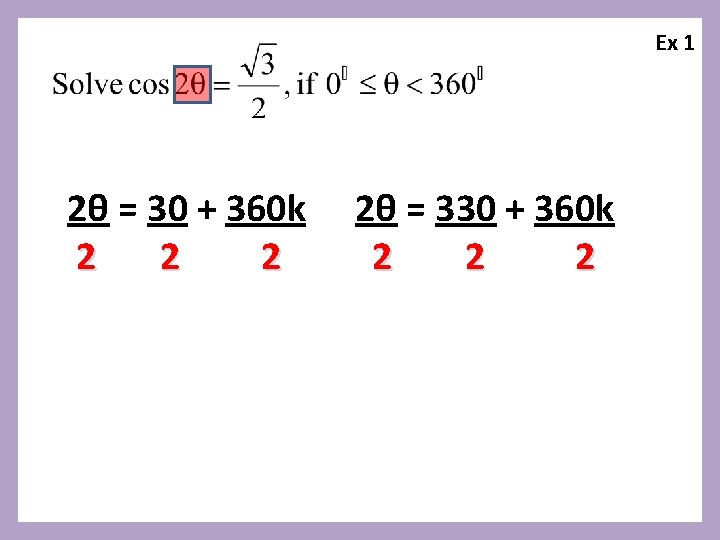
Ex 1 2θ = 30 + 360 k 2θ = 330 + 360 k We see that cos 2θ – being positive – is in Q I and Q IV. The reference angle is 30 o.

Ex 1 2θ = 30 + 360 k 2 2θ = 330 + 360 k 2 2 2

Ex 1 2θ = 30 + 360 k 2 2θ = 330 + 360 k 2 2 2 θ = 15 + 180 k θ = 165 + 180 k

Ex 1 2θ = 30 + 360 k 2 2θ = 330 + 360 k 2 2 2 θ = 15 + 180(0) θ = 165 + 180(0)

Ex 1 2θ = 30 + 360 k 2 2θ = 330 + 360 k 2 2 2 θ = 15 + 180(0) θ = 165 + 180(0) θ = 15, 165

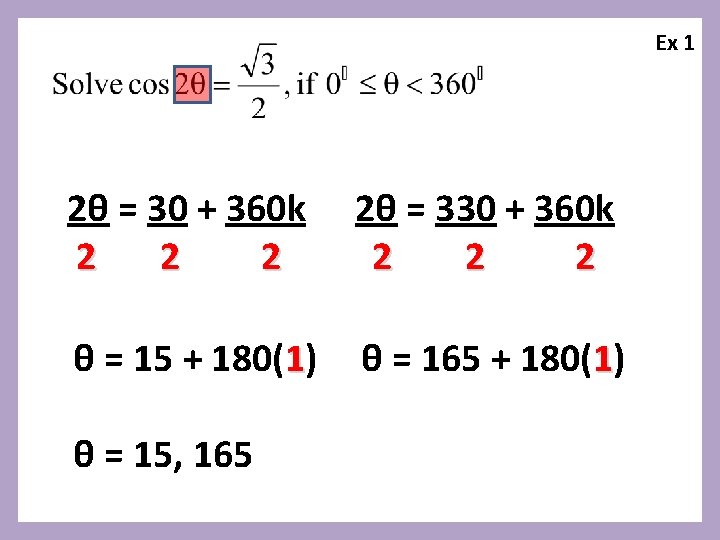
Ex 1 2θ = 30 + 360 k 2 2θ = 330 + 360 k 2 2 2 θ = 15 + 180(1) θ = 165 + 180(1) θ = 15, 165

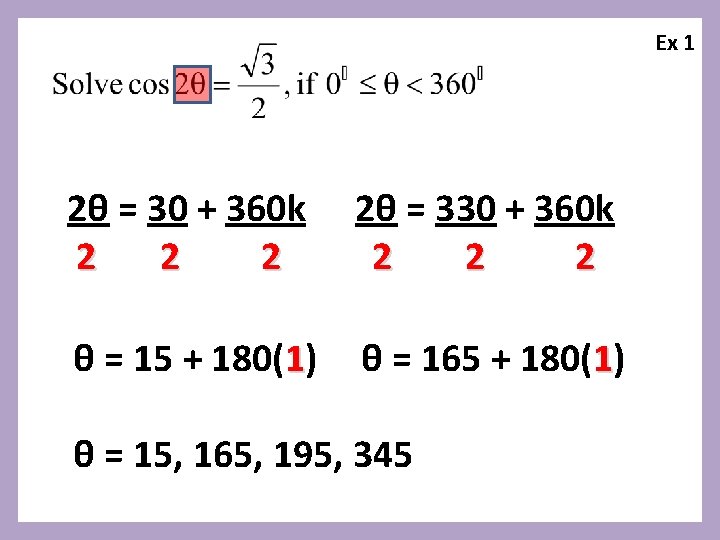
Ex 1 2θ = 30 + 360 k 2 2θ = 330 + 360 k 2 2 2 θ = 15 + 180(1) θ = 165 + 180(1) θ = 15, 165, 195, 345

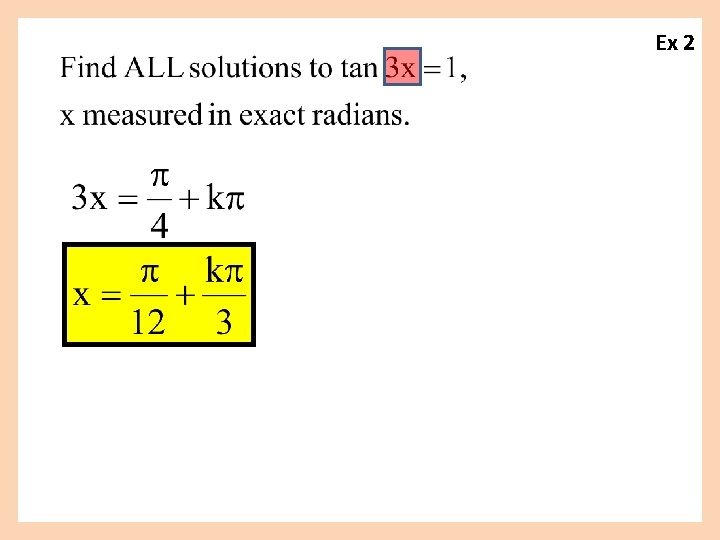
Ex 2

Ex 2 Remember, tangent has a period of π, not 2π.

Ex 2 Remember, tangent has a period of π, not 2π. Tan = 1 when the angle is 45 o.

Ex 2

Ex 2

Ex 2 If we wanted exact values between 0 and π, just let k = 0, 1, and 2.

Ex 2 If we wanted exact values between 0 and π, just let k = 0, 1, and 2.

# 11
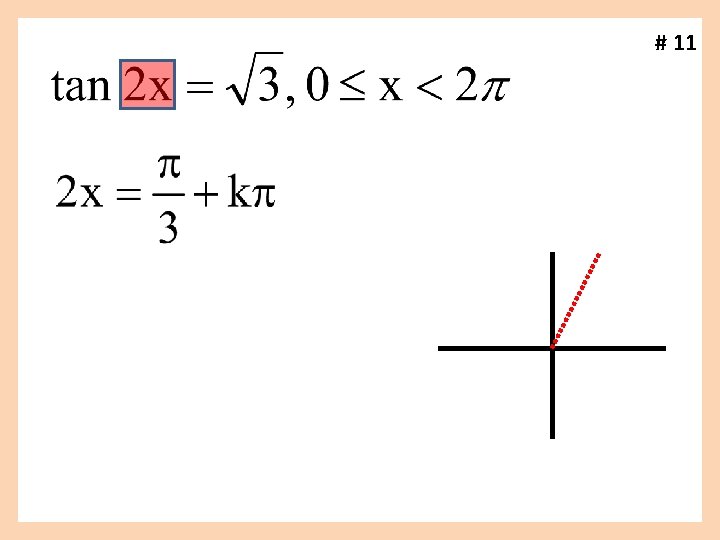
# 11

# 11

# 11
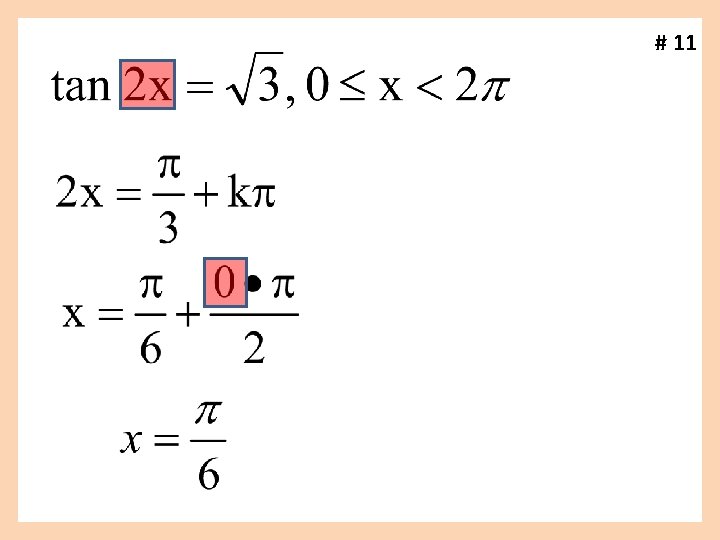
# 11

# 11

# 11
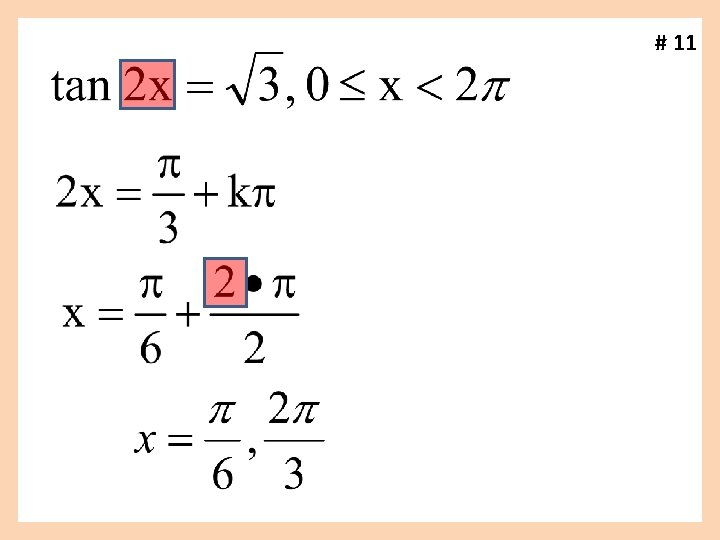
# 11
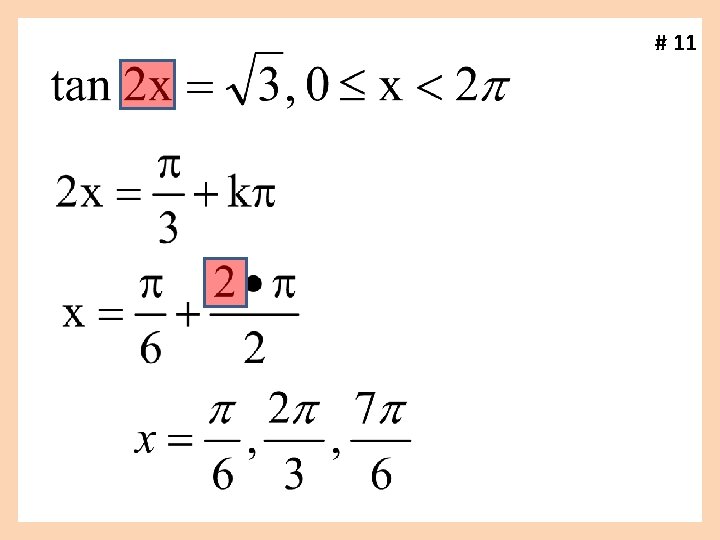
# 11
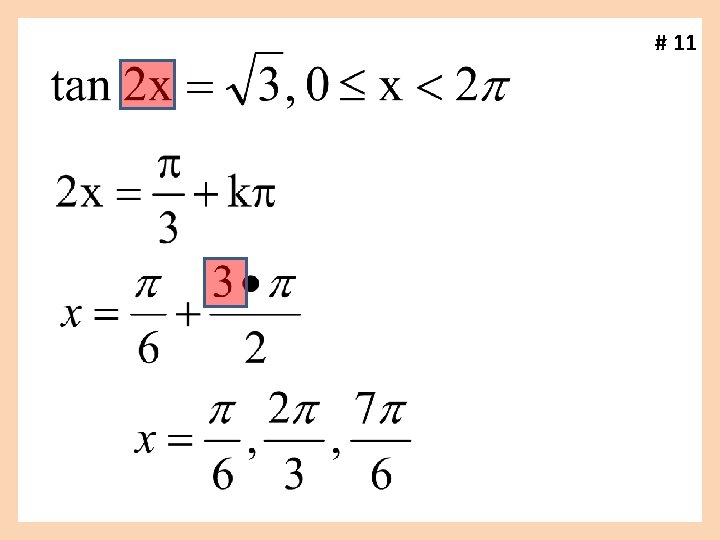
# 11
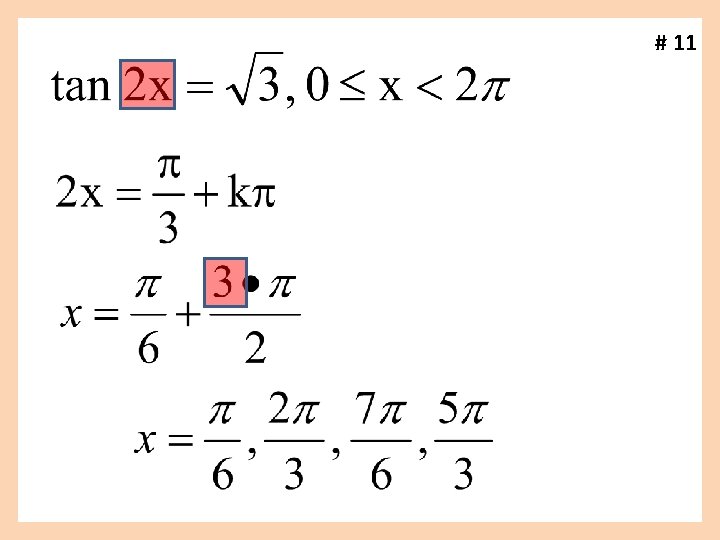
# 11

# 11

Ex 3
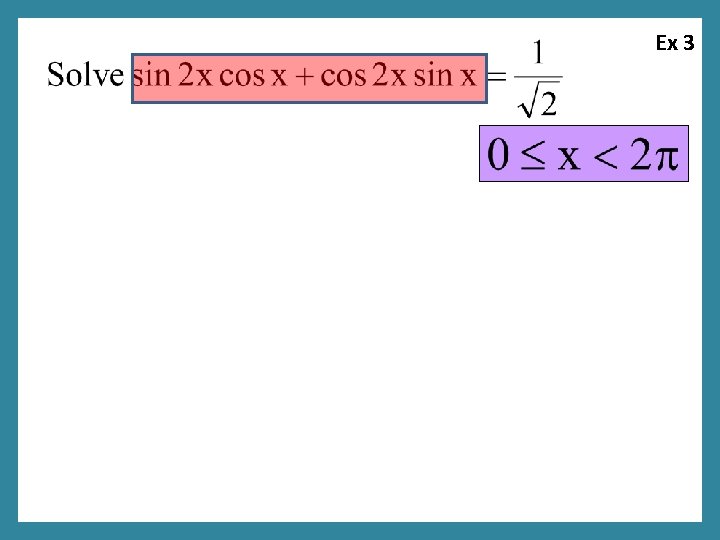
Ex 3

Ex 3 Do we recognize this “sum” formula?

Ex 3 Do we recognize this “sum” formula?

Ex 3
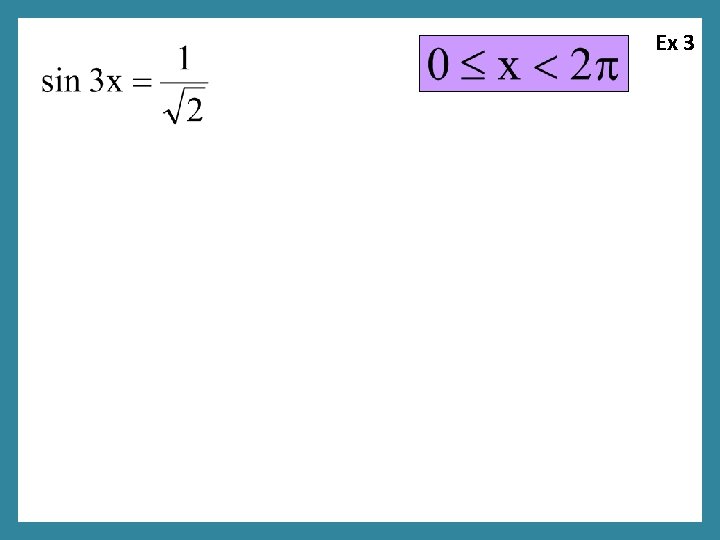
Ex 3
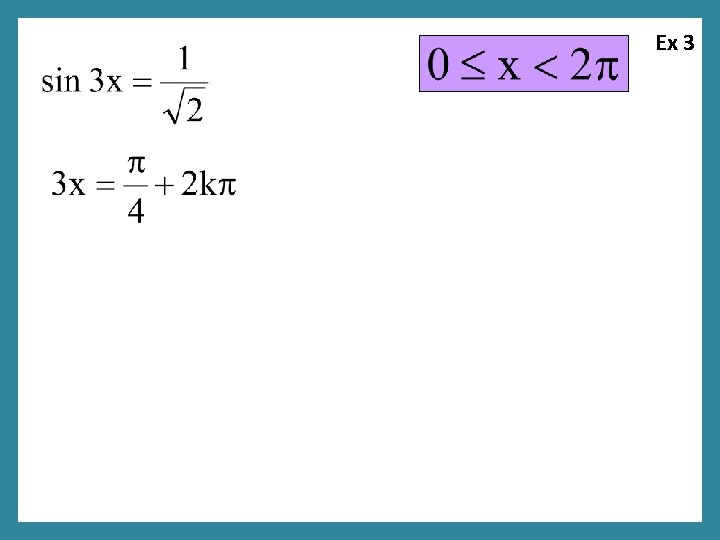
Ex 3
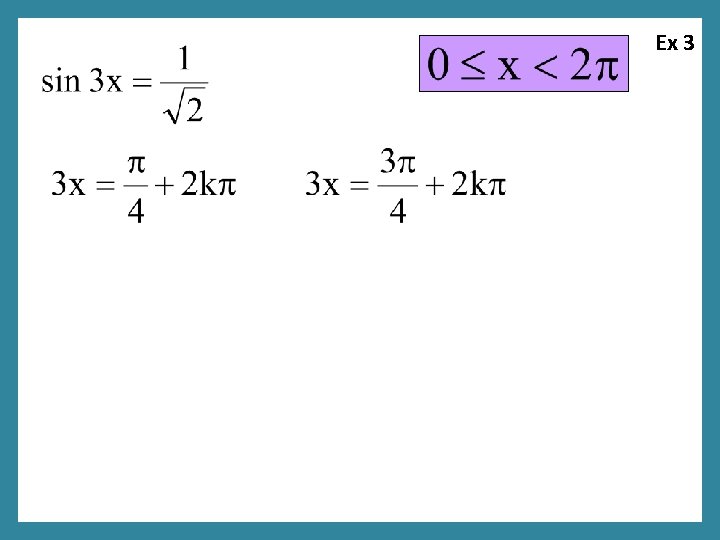
Ex 3
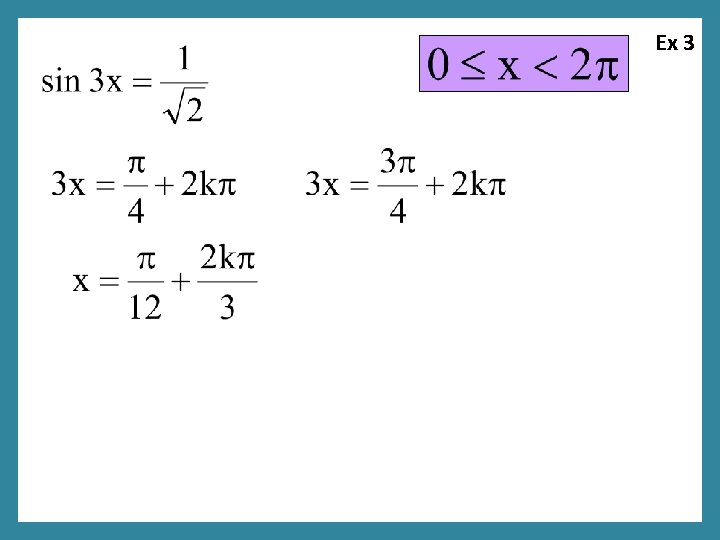
Ex 3
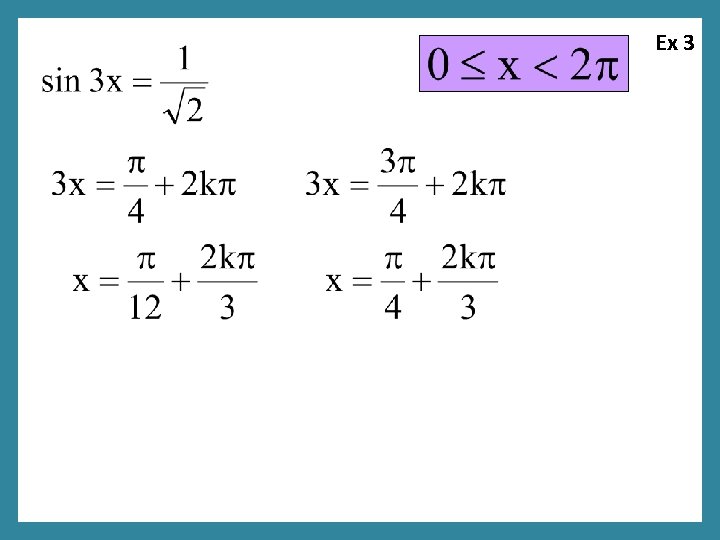
Ex 3

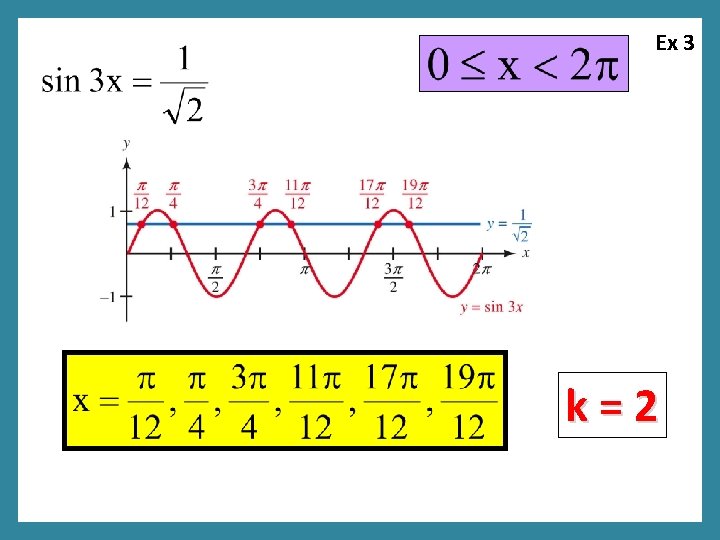
Ex 3 k=0

Ex 3 k=1

Ex 3 k=2

Ex 3 k=2

Ex 3 k=2
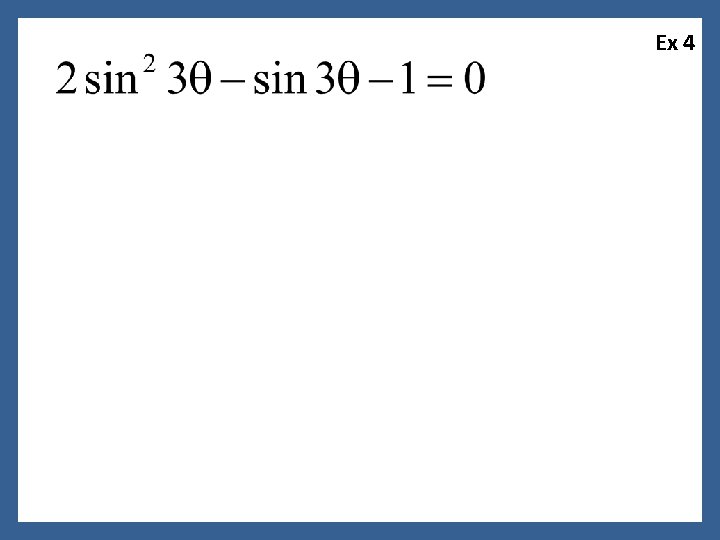
Ex 4

Ex 4 Find ALL solutions in degrees.

Ex 4 Find ALL solutions in degrees. We notice that this is in quadratic form.

Ex 4 (2 sin 3θ + 1)(sin 3θ – 1) = 0
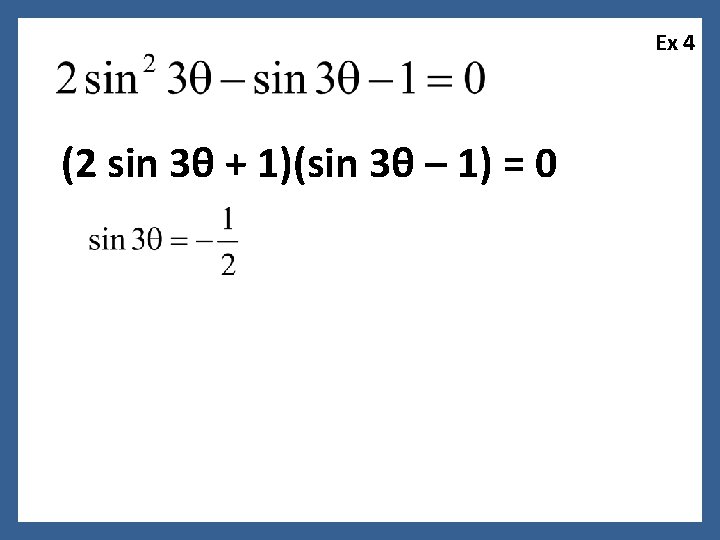
Ex 4 (2 sin 3θ + 1)(sin 3θ – 1) = 0
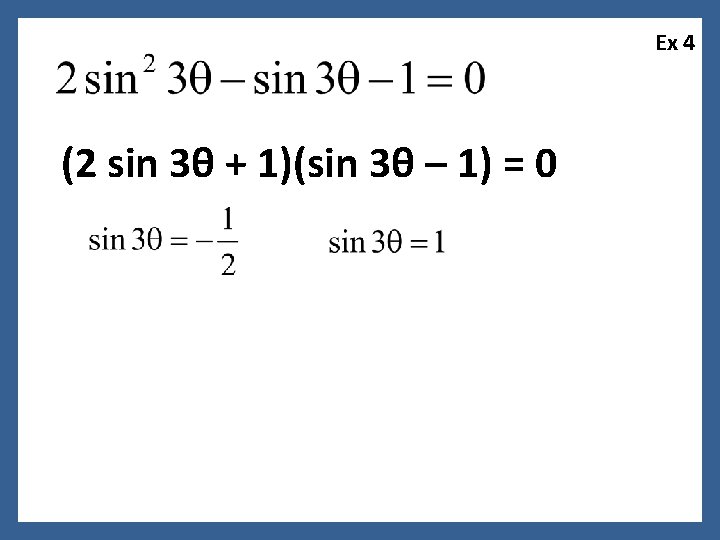
Ex 4 (2 sin 3θ + 1)(sin 3θ – 1) = 0

Ex 4 (2 sin 3θ + 1)(sin 3θ – 1) = 0 3θ = 210 + 360 k, 330 + 360 k

Ex 4 (2 sin 3θ + 1)(sin 3θ – 1) = 0 3θ = 210 + 360 k, 330 + 360 k, 90 + 360 k

Ex 4 (2 sin 3θ + 1)(sin 3θ – 1) = 0 3θ = 210 + 360 k, 330 + 360 k, 90 + 360 k θ = 70 + 120 k, 110 + 120 k, 30 + 120 k

Ex 4 (2 sin 3θ + 1)(sin 3θ – 1) = 0 3θ = 210 + 360 k, 330 + 360 k, 90 + 360 k θ = 70 + 120 k, 110 + 120 k, 30 + 120 k 30, 70, 110, 150, 190, 230, 270, 310, 350

Ex 4 (2 sin 3θ + 1)(sin 3θ – 1) = 0 3θ = 210 + 360 k, 330 + 360 k, 90 + 360 k θ = 70 + 120 k, 110 + 120 k, 30 + 120 k 30, 70, 110, 150, 190, 230, 270, 310, 350 SHORTCUT: 30 o + 40 k

Ex 5

Ex 5

Ex 5 Can we take the square roots of both sides?

Ex 5 Can we take the square roots of both sides?

Ex 5

Ex 5

Ex 5

Ex 5

Ex 6

Ex 6 In an earlier section, squaring both sides was a good idea. . . but it led to extraneous solutions.

Ex 6 In an earlier section, squaring both sides was a good idea. . . but it led to extraneous solutions.

Ex 6

Ex 6

Ex 6

Ex 6

Ex 6

Ex 6

Ex 6

Ex 6

Ex 6

Ex 6 θ = 0, 90, 180, 270

Ex 6 θ = 0, 90, 180, 270

Ex 6 θ = 0, 90, 180, 270

Ex 6 θ = 0, 90, 180, 270

Ex 6 θ = x 0, 90, 180, 270

Ex 6 θ = x 0, 90 180, 270

Ex 6 θ = x 0, 90 180, 270

Ex 6 √ θ = x 0, 90, 180, 270

Ex 6 √ θ = x 0, 90, 180 270

Ex 6 √ θ = x 0, 90, 180 270

Ex 6 √ √ θ = x 0, 90, 180, 270

Ex 6 √ √ θ = x 0, 90, 180, 270

Ex 6 √ √ θ = x 0, 90, 180, 270

Ex 6 √ √ x θ = x 0, 90, 180, 270

Homework 6. 3, p. 339 1 -55 odd
 What are the properties of vertically opposite angles
What are the properties of vertically opposite angles Sin cos derivative
Sin cos derivative Proofs involving angles
Proofs involving angles Quadratic logarithmic equations
Quadratic logarithmic equations 2-5 solving equations involving absolute value answer key
2-5 solving equations involving absolute value answer key 2-5 solving equations involving absolute value
2-5 solving equations involving absolute value Solving linear equations with fractions
Solving linear equations with fractions How to solve inverse trig functions
How to solve inverse trig functions Trig ratios for special angles
Trig ratios for special angles What are general angles
What are general angles How to solve trigonometric equations step by step
How to solve trigonometric equations step by step Trigonometric functions formula
Trigonometric functions formula Trigonometric identities
Trigonometric identities Table of trigonometric substitutions
Table of trigonometric substitutions Higher maths trig equations
Higher maths trig equations Delayed multiple baseline design
Delayed multiple baseline design Shared memory mimd architecture
Shared memory mimd architecture Example of adjacent complementary angles
Example of adjacent complementary angles Find the unknown labeled angles
Find the unknown labeled angles Module 15 angles and segments in circles
Module 15 angles and segments in circles Gv black
Gv black Solving quadratic equations multiple choice questions doc
Solving quadratic equations multiple choice questions doc Multiple absolute value equations
Multiple absolute value equations 9-3 practice polar and rectangular forms of equations
9-3 practice polar and rectangular forms of equations Translate word equations to chemical equations
Translate word equations to chemical equations How does nick characterize the guests at gatsby’s party?
How does nick characterize the guests at gatsby’s party? A figure of speech that makes a comparison
A figure of speech that makes a comparison Solving problems involving temperature
Solving problems involving temperature Parallel lines
Parallel lines Word problems involving similar triangles
Word problems involving similar triangles 5-5 practice inequalities involving absolute value answers
5-5 practice inequalities involving absolute value answers Deliquescent powders are.
Deliquescent powders are. Equilibrium involving thymol blue
Equilibrium involving thymol blue Absolute value inequalities and vs or
Absolute value inequalities and vs or Colligative properties example problems
Colligative properties example problems Theorems involving parallel lines
Theorems involving parallel lines Absolute value in a sentence
Absolute value in a sentence Logic operations involving binary images
Logic operations involving binary images Hinge theorem door justification
Hinge theorem door justification Kinetic energy of spring
Kinetic energy of spring Compare the given measures
Compare the given measures Consolidation is a process involving
Consolidation is a process involving Applications involving right triangles
Applications involving right triangles Inequalities in two triangles quiz
Inequalities in two triangles quiz Inequalities involving two triangles
Inequalities involving two triangles Statements and reason
Statements and reason Writing compound inequalities
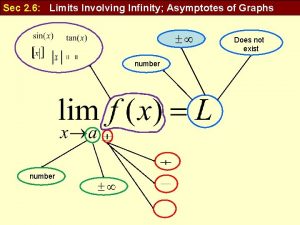
Writing compound inequalities Sec infinity
Sec infinity Real life examples of multiplication
Real life examples of multiplication What crisis occurs involving lydia
What crisis occurs involving lydia Equation for inverse variation
Equation for inverse variation Internal tourism includes
Internal tourism includes Involving families in the assessment process
Involving families in the assessment process Word problems with polynomials worksheet
Word problems with polynomials worksheet Vertical stretch exponential function
Vertical stretch exponential function 5-6 inequalities in two triangles
5-6 inequalities in two triangles Asl commands involving objects
Asl commands involving objects Enzyme station activity answer key
Enzyme station activity answer key Role of intermediaries in service delivery
Role of intermediaries in service delivery Trading strategies involving options
Trading strategies involving options Http overview
Http overview Real life problems involving parallelogram
Real life problems involving parallelogram Wars involving us
Wars involving us Integrals involving powers of secant and tangent
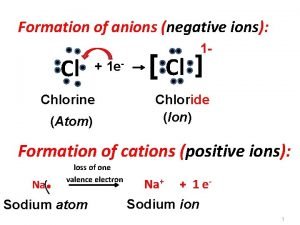
Integrals involving powers of secant and tangent Cl negative ion
Cl negative ion What are the processes involving river transportation
What are the processes involving river transportation Lim as x approaches infinity
Lim as x approaches infinity You and your friend both solve a problem involving a skier
You and your friend both solve a problem involving a skier Pythagorean identities
Pythagorean identities Sohcahtoa choshacao
Sohcahtoa choshacao Limit rules
Limit rules Relative frequency two way table
Relative frequency two way table Trig ratio scavenger hunt
Trig ratio scavenger hunt Reciprocal trig functions
Reciprocal trig functions Magic triangle trigonometry
Magic triangle trigonometry National 5 trig identities
National 5 trig identities Hyperbolic trig substitution
Hyperbolic trig substitution Cos de 90
Cos de 90 Trig ratio scavenger hunt
Trig ratio scavenger hunt Trig form
Trig form Pythagorean identities
Pythagorean identities Trig cancellation property
Trig cancellation property What are the 6 trig functions
What are the 6 trig functions Trig quadrant
Trig quadrant Trig transformations
Trig transformations Convert to trigonometric form -8i
Convert to trigonometric form -8i @mathemateg
@mathemateg As 91575
As 91575 As 91575
As 91575 Transformations of sine and cosine functions
Transformations of sine and cosine functions Desmos trig graphing calculator
Desmos trig graphing calculator Double angle
Double angle Common trig identities
Common trig identities Inverse trig table
Inverse trig table 4-1 right triangle trigonometry word problems
4-1 right triangle trigonometry word problems Hot air balloon trig problem
Hot air balloon trig problem