While you wait Trigonometric Identities and Equations Section

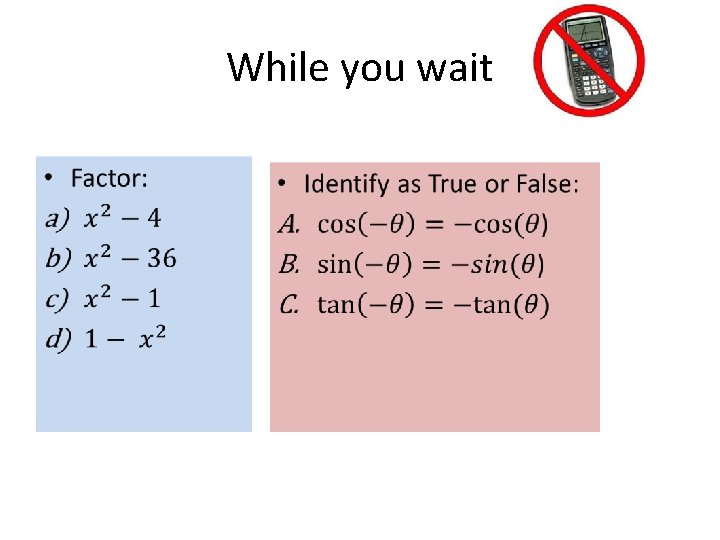
While you wait: •

Trigonometric Identities and Equations Section 8. 4

See page 318 Cofuntion Relationships

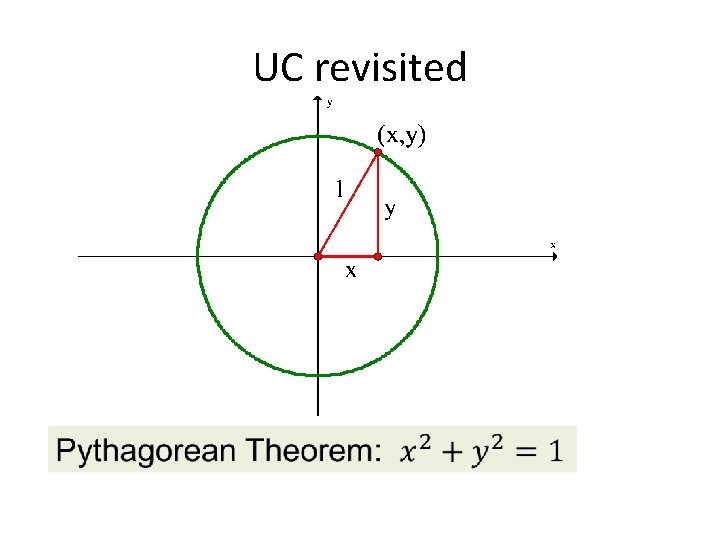
UC revisited

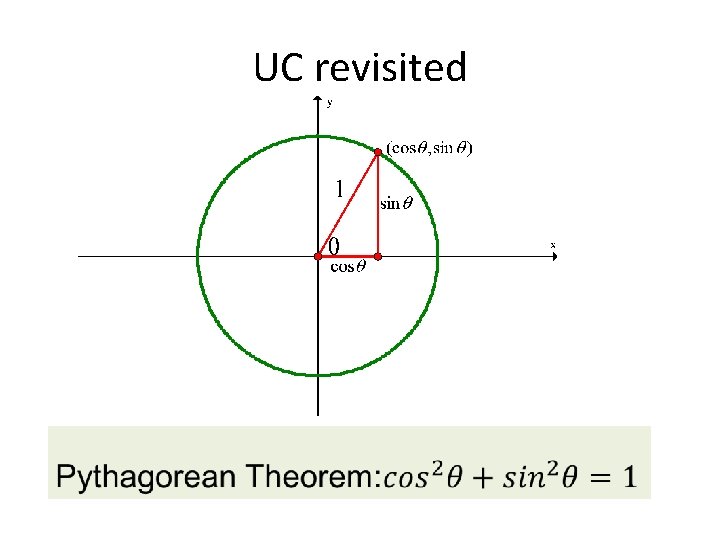
UC revisited

The trig relationships: •

• An identity is an equation that is true for all values of the variables. • Difference between identity and equation: • An identity is true for any value of the variable, but an equation is not. For example the equation 3 x=12 is true only when x=4, so it is an equation, but not an identity.

What are identities used for? • They are used in simplifying or rearranging algebraic expressions. • By definition, the two sides of an identity are interchangeable, so we can replace one with the other at any time. • In this section we will study identities with trig functions.

The trigonometry identities • There are dozens of identities in the field of trigonometry. • Many websites list the trig identities. Many websites will also explain why identities are true. i. e. prove the identities. • For an example of such a site: click here

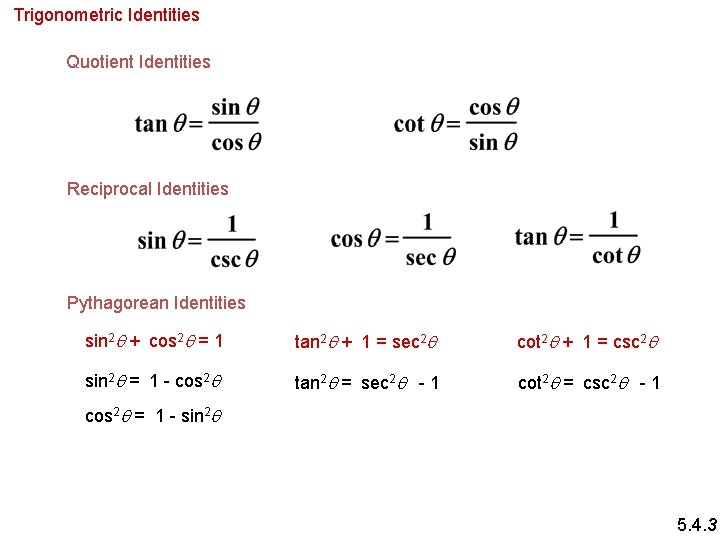
Trigonometric Identities Quotient Identities Reciprocal Identities Pythagorean Identities sin 2 q + cos 2 q = 1 tan 2 q + 1 = sec 2 q cot 2 q + 1 = csc 2 q sin 2 q = 1 - cos 2 q tan 2 q = sec 2 q - 1 cot 2 q = csc 2 q - 1 cos 2 q = 1 - sin 2 q 5. 4. 3

Where did our pythagorean identities come from? ? Do you remember the Unit Circle? • What is the equation for the unit circle? x 2 + y 2 = 1 • What does x = ? What does y = ? (in terms of trig functions) sin 2θ + cos 2θ = 1 Pythagorean Identity!

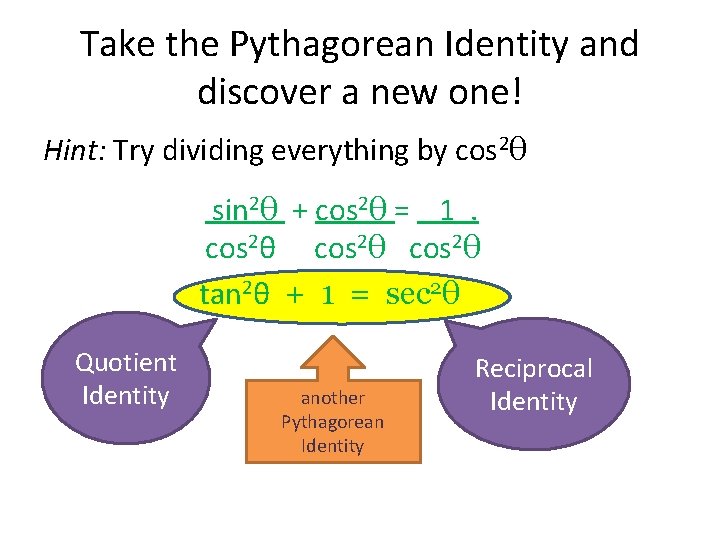
Take the Pythagorean Identity and discover a new one! Hint: Try dividing everything by cos 2θ sin 2θ + cos 2θ = 1 . cos 2θ tan 2θ + 1 = sec 2θ Quotient Identity another Pythagorean Identity Reciprocal Identity

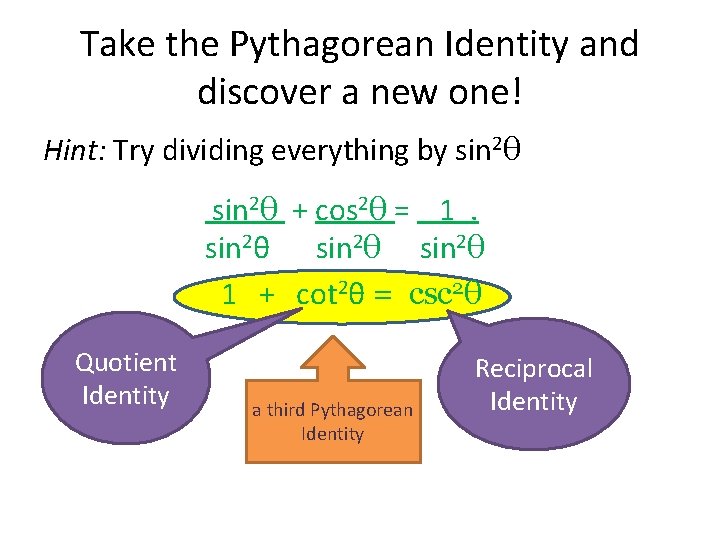
Take the Pythagorean Identity and discover a new one! Hint: Try dividing everything by sin 2θ + cos 2θ = 1 . sin 2θ 1 + cot 2θ = csc 2θ Quotient Identity a third Pythagorean Identity Reciprocal Identity

Simplifying Trigonometric Expressions Identities can be used to simplify trigonometric expressions. Simplify. a) b) 5. 4. 5

• Practice Problems for Day 1: refer to class handout.

While you wait • •

Proving a Trigonometric Identity: 1. Transform the right side of the identity into the left side, 2. Vice versa (Left side to Right ) We do not want to use properties from algebra that involve both sides of the identity.

Guidelines for Proving Identities: 1. It is usually best to work on the more complicated side first. 2. Look for trigonometric substitutions involving the basic identities that may help simplify things. 3. Look for algebraic operations, such as adding fractions, the distributive property, or factoring, that may simplify the side you are working with or that will at least lead to an expression that will be easier to simplify.

4. If you cannot think of anything else to do, change everything to sines and cosines and see if that helps. 5. Always keep an eye on the side you are not working with to be sure you are working toward it. There is a certain sense of direction that accompanies a successful proof. 6. Practice, practice!

Prove •

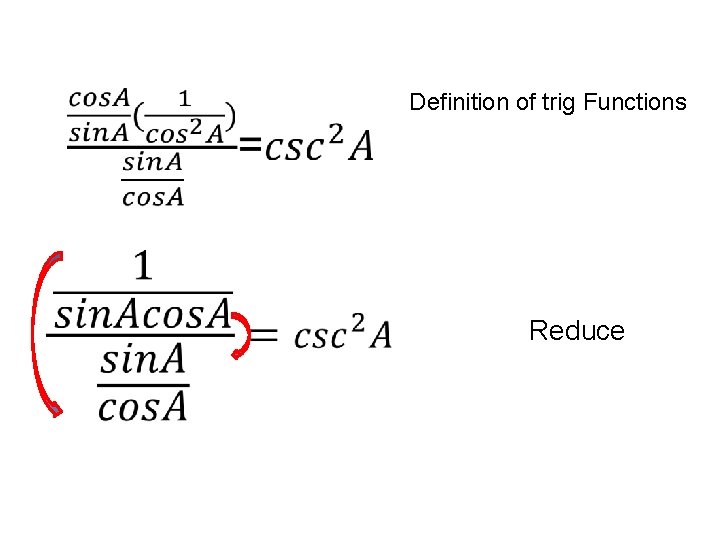
Definition of trig Functions Reduce

Reduce Def of trig function.

Practice Problems Day 2 Sec 8 - Written Exercises page 321 #13 -19 odds; 29 -35 odds Exit Question: #3 b the handout. A complete, step by step solution must be included.

Using the identities you now know, find the trig value. 1. ) If cosθ = 3/4, find secθ 2. ) If cosθ = 3/5, find cscθ.

3. ) sinθ = -1/3, find tanθ 4. ) secθ = -7/5, find sinθ

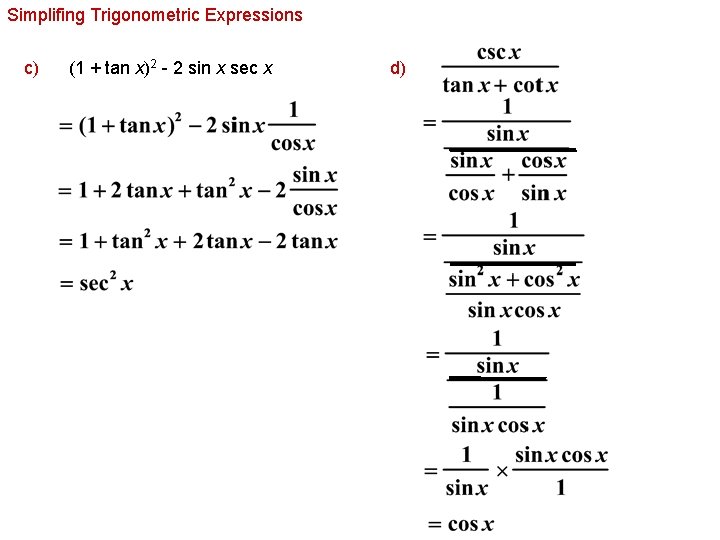
Simplifing Trigonometric Expressions c) (1 + tan x)2 - 2 sin x sec x d)

Simplify each expression.

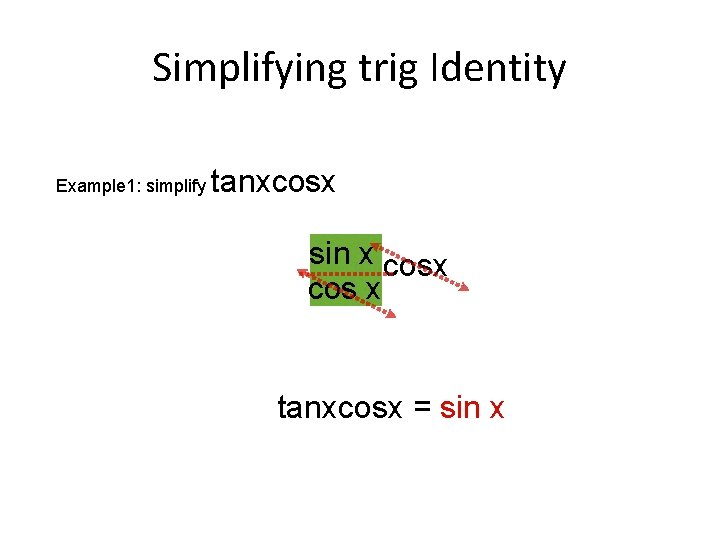
Simplifying trig Identity Example 1: simplify tanxcosx sin x tanx cos x tanxcosx = sin x

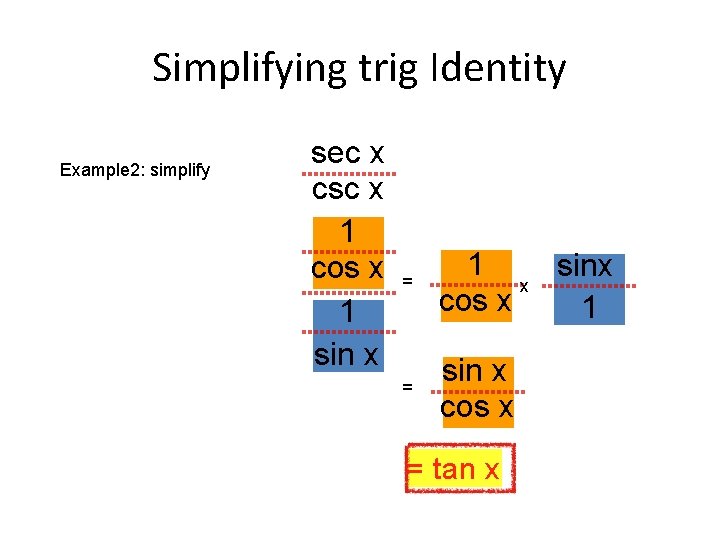
Simplifying trig Identity Example 2: simplify sec x csc x 1 cos x sec x csc x 1 sin x = 1 sinx x cos x 1 = sin x cos x = tan x

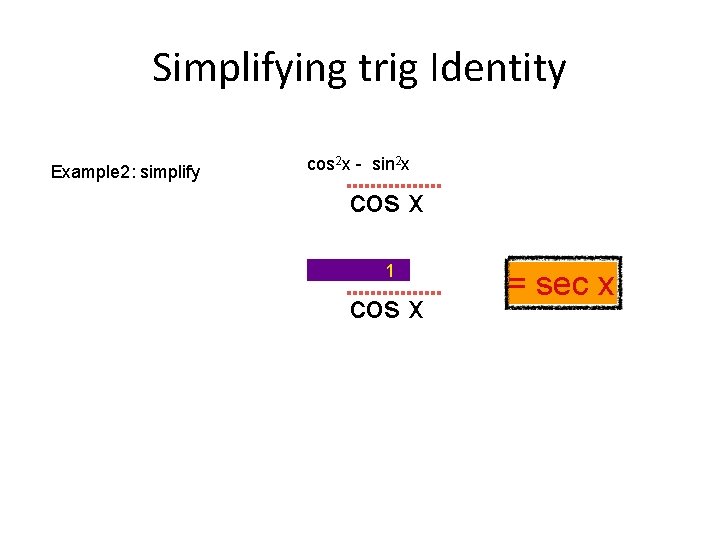
Simplifying trig Identity Example 2: simplify cos 2 x - sin 2 x cos x cos 2 x - sin 12 x cos x = sec x

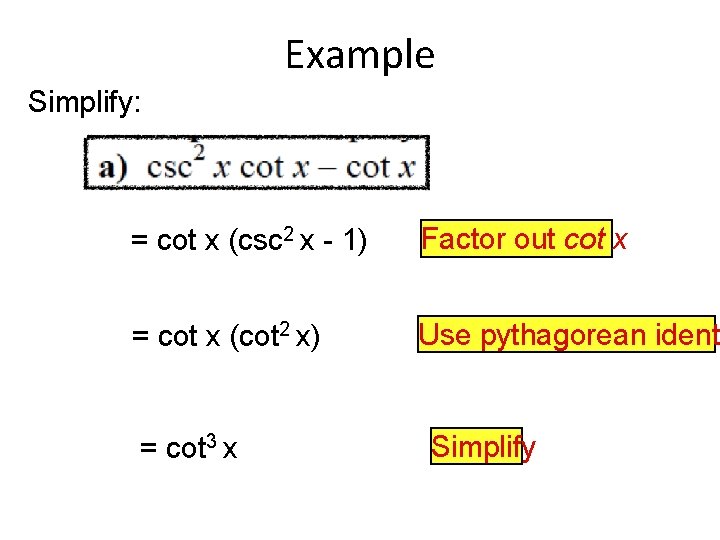
Example Simplify: = cot x (csc 2 x - 1) Factor out cot x = cot x (cot 2 x) Use pythagorean identi = cot 3 x Simplify

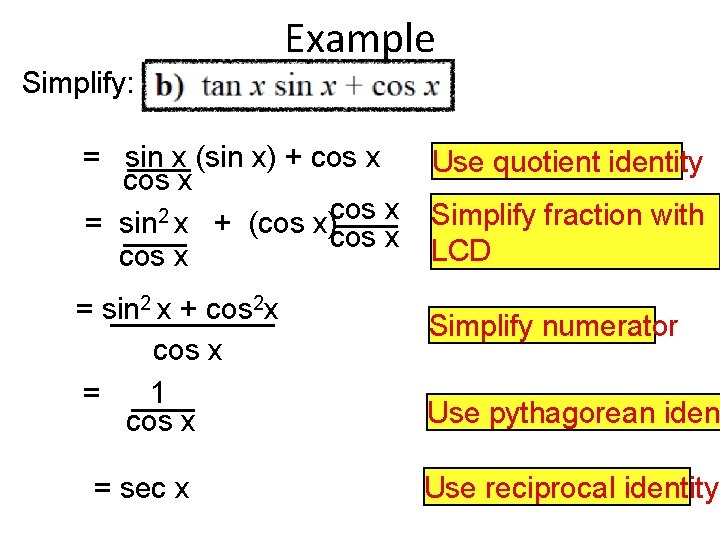
Example Simplify: = sin x (sin x) + cos x 2 = sin x + (cos x)cos x = sin 2 x + cos 2 x cos x = 1 cos x = sec x Use quotient identity Simplify fraction with LCD Simplify numerator Use pythagorean iden Use reciprocal identity

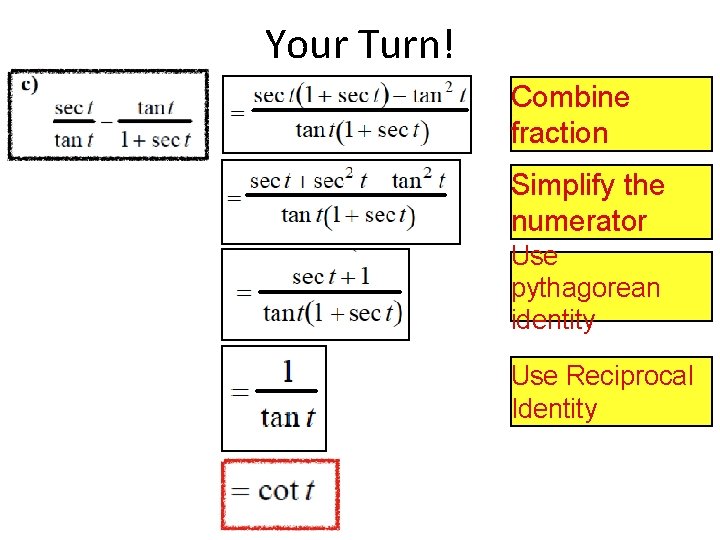
Your Turn! Combine fraction Simplify the numerator Use pythagorean identity Use Reciprocal Identity

Practice 1 cos 2θ cosθ sin 2θ cos 2θ secθ-cosθ csc 2θ cotθ tan 2θ

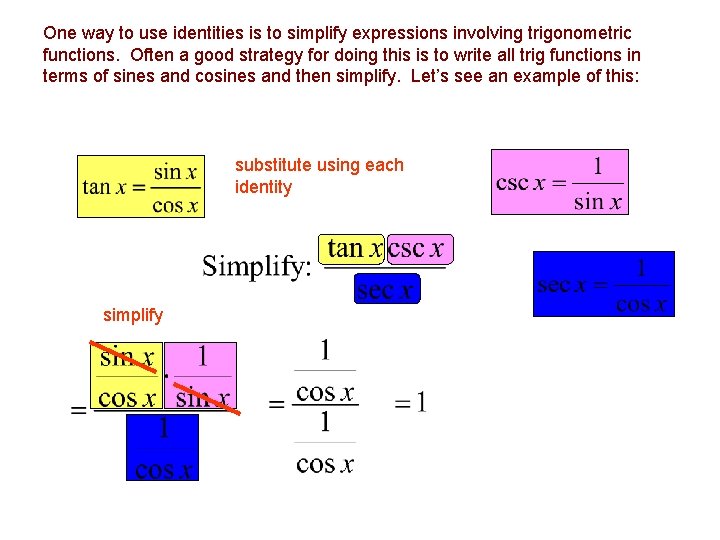
One way to use identities is to simplify expressions involving trigonometric functions. Often a good strategy for doing this is to write all trig functions in terms of sines and cosines and then simplify. Let’s see an example of this: substitute using each identity simplify

Another way to use identities is to write one function in terms of another function. Let’s see an example of this: This expression involves both sine and cosine. The Fundamental Identity makes a connection between sine and cosine so we can use that and solve for cosine squared and substitute.

(E) Examples • Prove tan(x) cos(x) = sin(x) 38

(E) Examples • Prove tan 2(x) = sin 2(x) cos-2(x) 39

(E) Examples • Prove 40

(E) Examples • Prove 41