Two Way Frequency Tables Warm Up Trig Review

Two Way Frequency Tables

Warm Up: Trig Review �
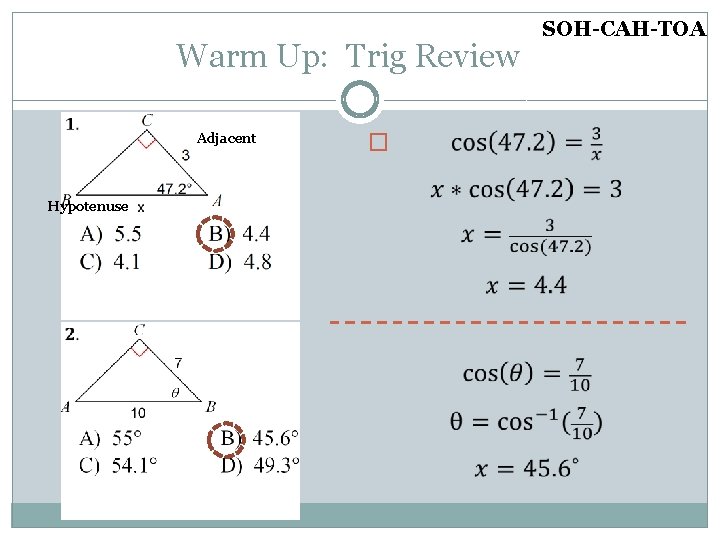
Warm Up: Trig Review Hypotenuse Adjacent � SOH-CAH-TOA

Warm Up: Trig Review SOH-CAH-TOA �

Two Way Frequency Tables Objective DOL SWBAT construct and analyze two-way tables. Given 2 CR problems, SW construct and analyze two-way tables with 80% accuracy. EQ: How can we represent information?

Let them eat cake _________ Everything else What’s the best kind of cake?

Let them eat cake _________ Everything else What’s better: Cake or cupcakes? Cake Cupcakes

Two Way Frequency Tables Everything else _________ Complete the table based on our data. Cake Cupcakes Total Everything else Total Cake Cupcakes

Two Way Frequency Tables Two way frequency tables: Show data in a way that lets us make comparisons For example… Cake Cupcakes Total Everything else Total • How many students preferred our most popular flavor? • How many students preferred cupcakes? • If we’re just making dessert for the students who preferred our most popular flavor, should we make cake or cupcakes?
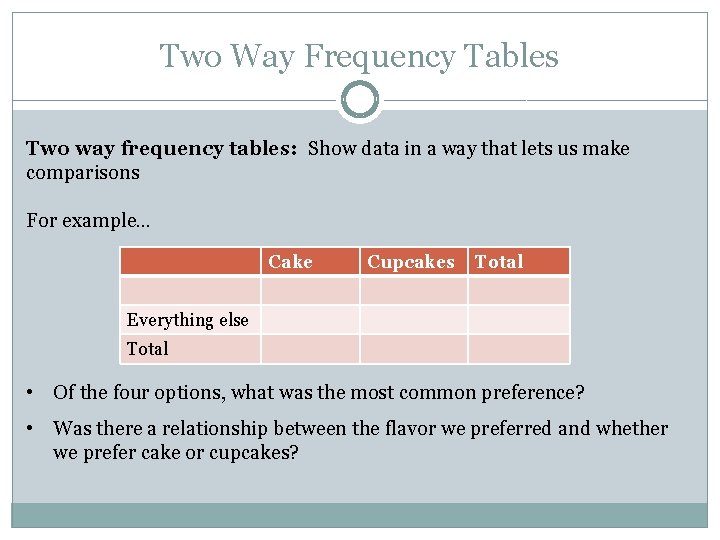
Two Way Frequency Tables Two way frequency tables: Show data in a way that lets us make comparisons For example… Cake Cupcakes Total Everything else Total • Of the four options, what was the most common preference? • Was there a relationship between the flavor we preferred and whether we prefer cake or cupcakes?

Example: Rainy Day Fun �The Summer Camp for Kids staff is planning an indoor activity for the campers to do on rainy days. �They are considering a Lego activity and a finger painting activity. �They sent out a survey to all the kids who will be coming to the camp to find out their preferences.
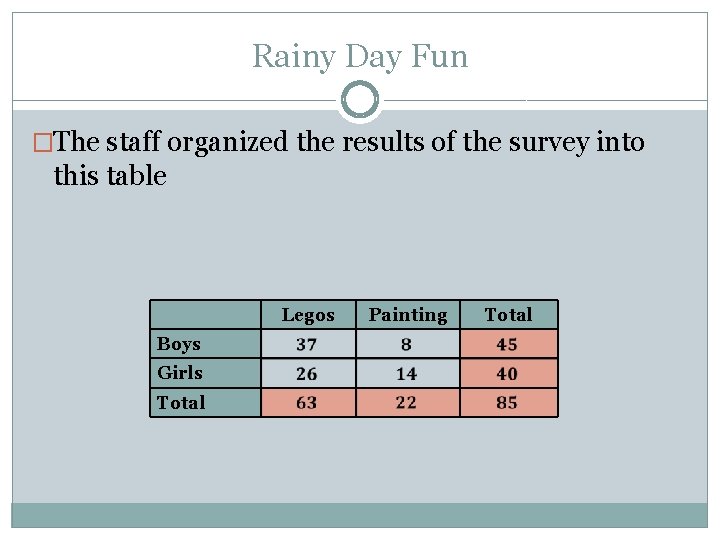
Rainy Day Fun �The staff organized the results of the survey into this table Legos Boys Girls Total Painting Total
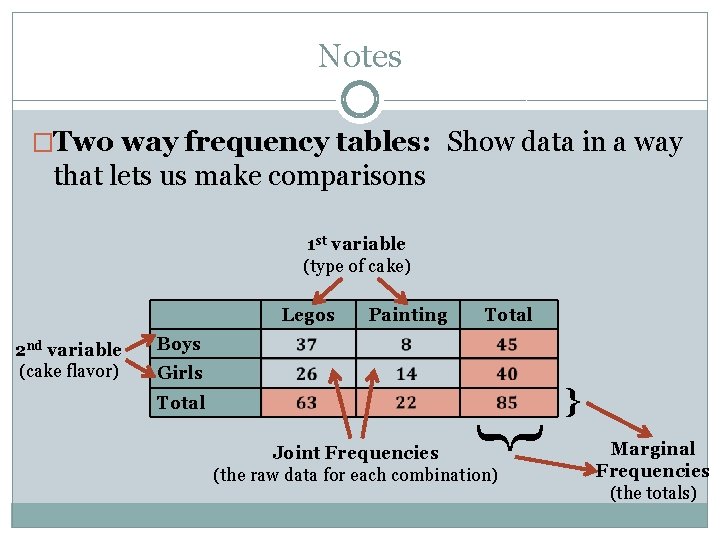
Notes �Two way frequency tables: Show data in a way that lets us make comparisons 1 st variable (type of cake) Legos 2 nd variable (cake flavor) Painting Total Boys Girls } Total } Joint Frequencies (the raw data for each combination) Marginal Frequencies (the totals)
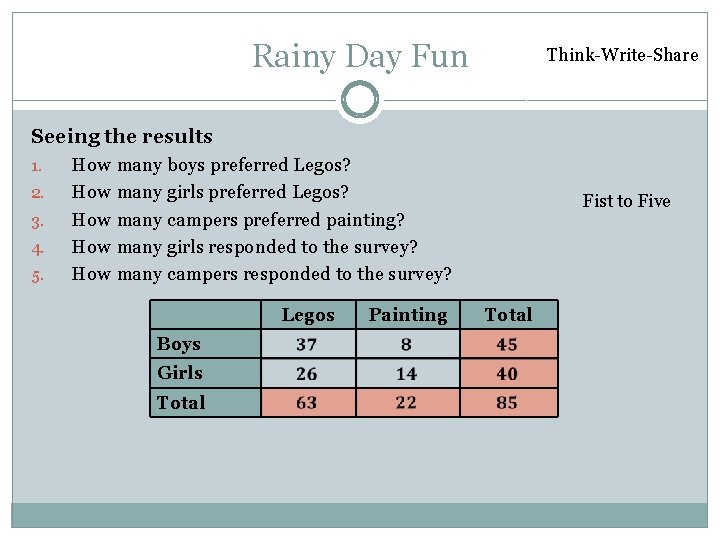
Rainy Day Fun Think-Write-Share Seeing the results 1. 2. 3. 4. 5. How many boys preferred Legos? How many girls preferred Legos? How many campers preferred painting? How many girls responded to the survey? How many campers responded to the survey? Legos Boys Girls Total Painting Fist to Five Total

Rainy Day Fun What’s wrong with this interpretation? � More boys prefer Legos (37 to 26) � More girls prefer painting (14 to 8) � Therefore, they should let boys to Legos and girls paint Write your response on your whiteboard. Legos Boys Girls Total Painting Total
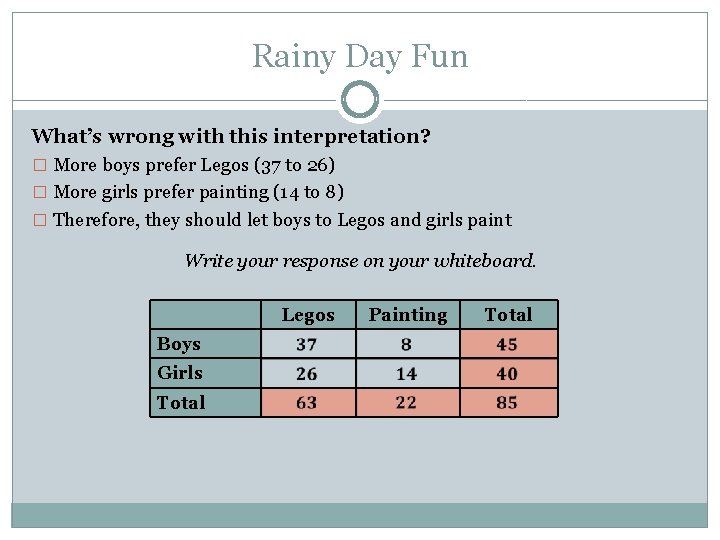
Rainy Day Fun What’s wrong with this interpretation? � More boys prefer Legos (37 to 26) � More girls prefer painting (14 to 8) � Therefore, they should let boys to Legos and girls paint Write your response on your whiteboard. Legos Boys Girls Total Painting Total

Finding Missing Information

Key Club Fundraising The Key Club will sell candy as a fundraiser. They surveyed 80 students about their favorite candy. The results are shown in the frequency table. Fill in the missing information. Lollipop Boys Peanut Butter Cup Total Girls Total Whiteboards: Cell by cell First, what do you know about the grand total?
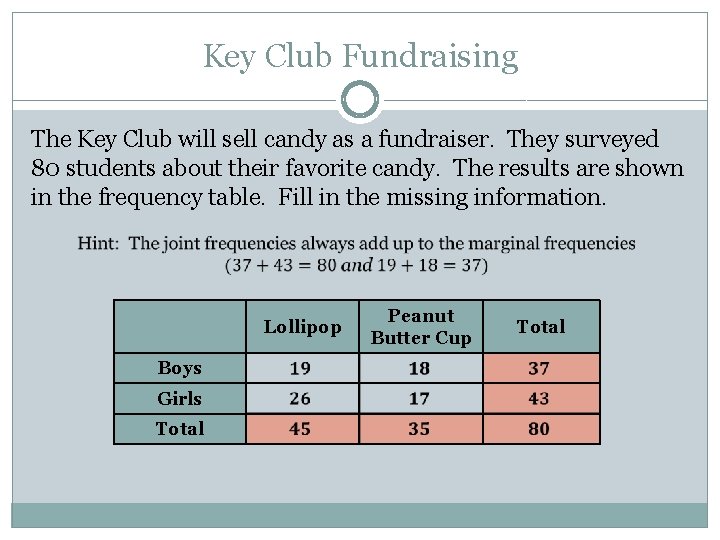
Key Club Fundraising The Key Club will sell candy as a fundraiser. They surveyed 80 students about their favorite candy. The results are shown in the frequency table. Fill in the missing information. Lollipop Boys Girls Total Peanut Butter Cup Total

Two Way Relative Frequency Tables BACK TO SUMMER CAMP
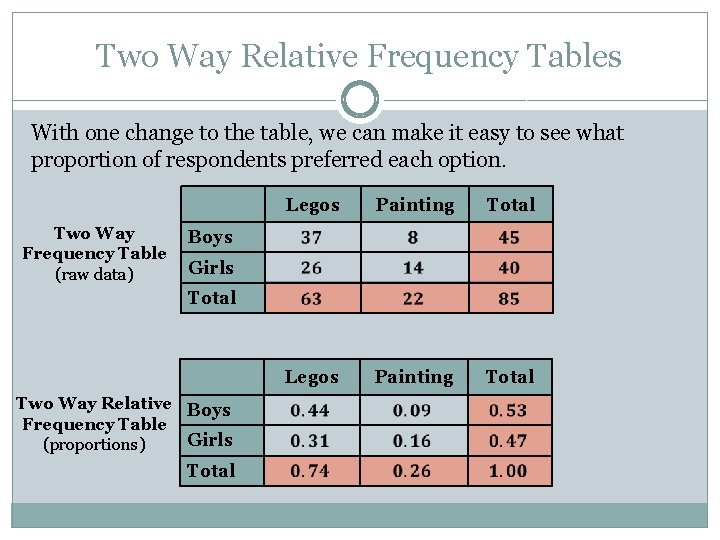
Two Way Relative Frequency Tables With one change to the table, we can make it easy to see what proportion of respondents preferred each option. Two Way Frequency Table (raw data) Legos Painting Total Boys Girls Total Two Way Relative Boys Frequency Table Girls (proportions) Total
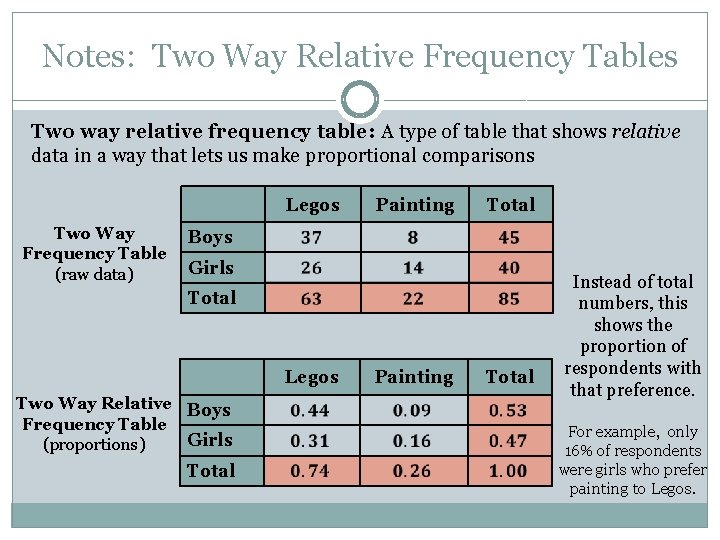
Notes: Two Way Relative Frequency Tables Two way relative frequency table: A type of table that shows relative data in a way that lets us make proportional comparisons Legos Two Way Frequency Table (raw data) Painting Total Boys Girls Total Legos Two Way Relative Boys Frequency Table Girls (proportions) Total Painting Total Instead of total numbers, this shows the proportion of respondents with that preference. For example, only 16% of respondents were girls who prefer painting to Legos.
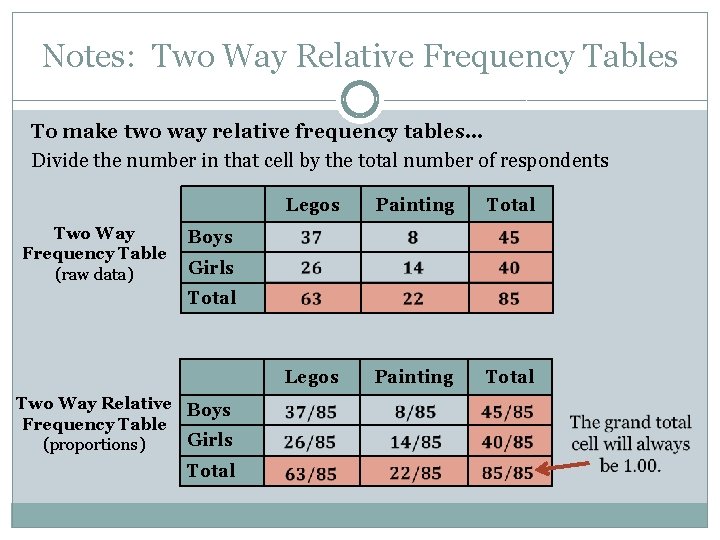
Notes: Two Way Relative Frequency Tables To make two way relative frequency tables… Divide the number in that cell by the total number of respondents Two Way Frequency Table (raw data) Legos Painting Total Boys Girls Total Two Way Relative Boys Frequency Table Girls (proportions) Total
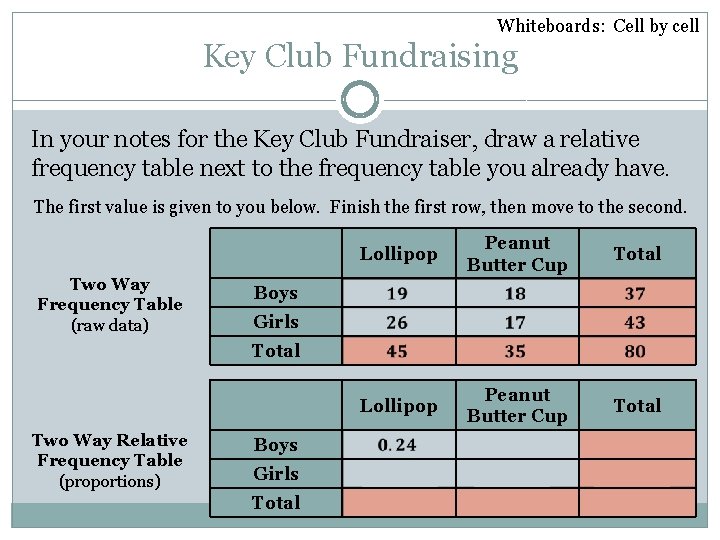
Whiteboards: Cell by cell Key Club Fundraising In your notes for the Key Club Fundraiser, draw a relative frequency table next to the frequency table you already have. The first value is given to you below. Finish the first row, then move to the second. Two Way Frequency Table (raw data) Lollipop Peanut Butter Cup Total Boys Girls Total Two Way Relative Frequency Table (proportions) Boys Girls Total
Constructing Tables

Chocolates and Caramels Lena has a box of 18 chocolate and caramel candies. � 10 candies have chocolate and caramel � 3 candies have neither chocolate nor caramel � 12 candies have chocolate Complete the table given this information. Step 1. Make a table Step 2. Fill in the given values Step 3. Calculate the missing values Caramel No caramel Total Chocolate No chocolate Total

Soccer vs. Football ESPN surveyed 50 respondents from the United States and Mexico about whether they prefer soccer or football. � 26 people from the United States responded � 8 people from the United States preferred soccer � 23 people from Mexico preferred soccer Given this information, complete the two way frequency table and the two way relative frequency table. Step 1. Make a table Step 2. Fill in the given values Step 3. Calculate the missing values
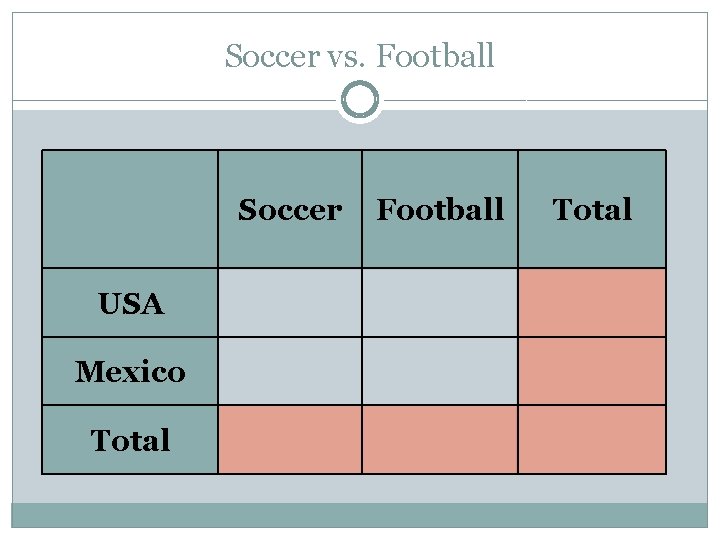
Soccer vs. Football Soccer USA Football Total Mexico Total

Soccer vs. Football 1. How many people from Mexico responded? 2. Were both countries evenly represented? Why? 3. What does the number 18 represent? 4. Which sport is more popular overall? 5. What patterns do you see in the data? 6. What percent of U. S. respondents prefer soccer? 7. What is the meaning of each marginal frequency?

Cats and Dogs A new Wal-Mart surveyed 75 people in the neighborhood about their pets. � 25 people have a dog � 20 people have a cat � 9 people have a cat and a dog Given this information, complete the two way frequency table and the two way relative frequency table. Step 1. Make a table Step 2. Fill in the given values Step 3. Calculate the missing values
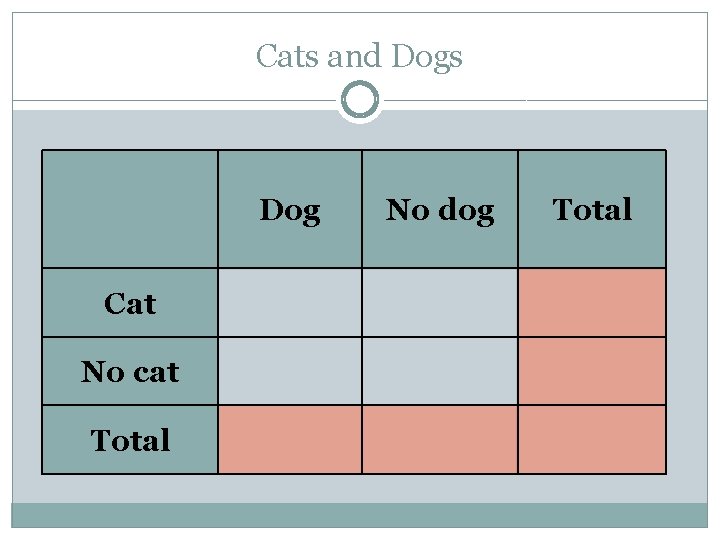
Cats and Dogs Dog Cat No dog Total No cat Total

Cats and Dogs 1. How many respondents have no dog? 2. What percent of respondents have no pet? 3. How common is it to have a cat and dog? 4. What does the number 55 represent? 5. Which animal is more popular? Why? 6. What patterns do you see in the data?
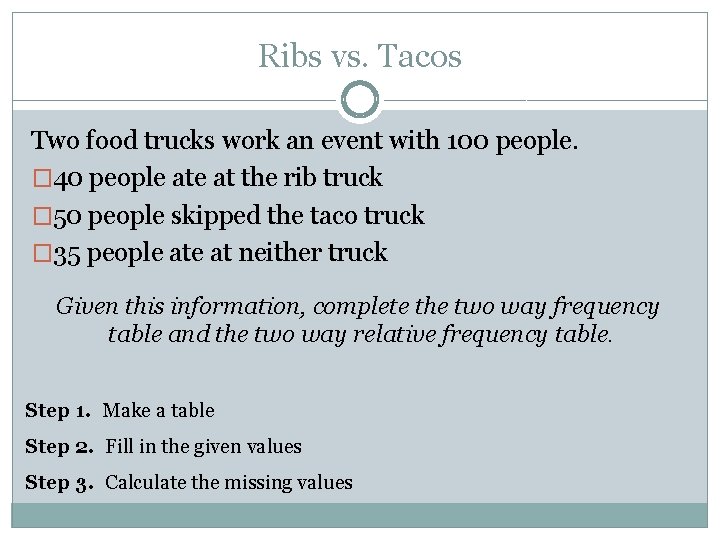
Ribs vs. Tacos Two food trucks work an event with 100 people. � 40 people at the rib truck � 50 people skipped the taco truck � 35 people at neither truck Given this information, complete the two way frequency table and the two way relative frequency table. Step 1. Make a table Step 2. Fill in the given values Step 3. Calculate the missing values
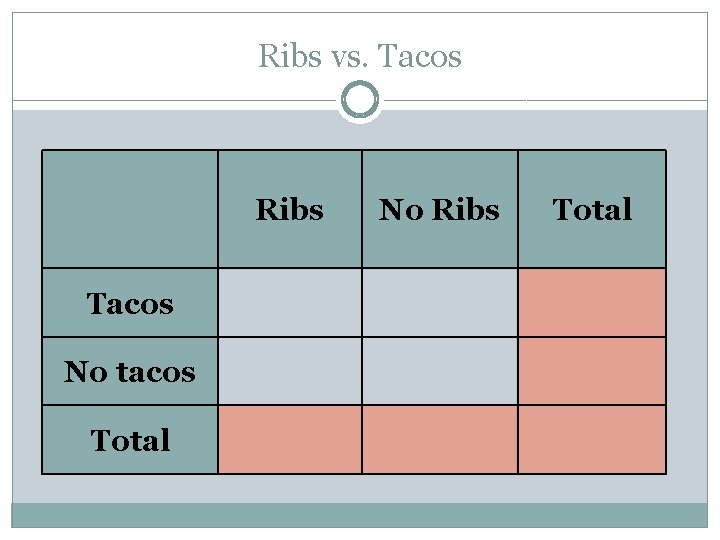
Ribs vs. Tacos Ribs Tacos No Ribs Total No tacos Total

Ribs vs. Tacos 1. Looking at all four joint frequencies, what was the most popular option? 2. What was the second most popular option? 3. What does the number 15 represent? 4. What percent of people had no ribs? 5. What do the marginal frequencies represent? 6. What patterns do you see in the data?

Practice

Key Club Fundraising WB checks 45 How many students preferred lollipops? 2. How many girls preferred peanut butter cups? 17 37 3. How many boys answered the survey? 4. Were boys and girls both evenly represented? Why? 1. Boys and girls were represented fairly evenly because about the same number of boys and girls responded. Lollipop Boys Girls Total Peanut Butter Cup Total

Key Club Fundraising WB checks 5. Explain what the number 19 means in this table. 19 represents the number of boys who preferred lollipops. 6. Explain what the number 35 means in this table. 35 represents the total number of people who preferred peanut butter cups. Lollipop Boys Girls Total Peanut Butter Cup Total
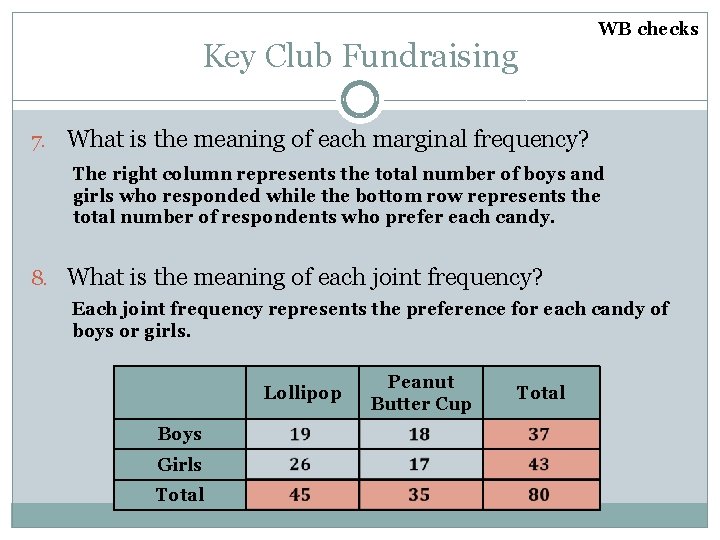
Key Club Fundraising WB checks 7. What is the meaning of each marginal frequency? The right column represents the total number of boys and girls who responded while the bottom row represents the total number of respondents who prefer each candy. 8. What is the meaning of each joint frequency? Each joint frequency represents the preference for each candy of boys or girls. Lollipop Boys Girls Total Peanut Butter Cup Total

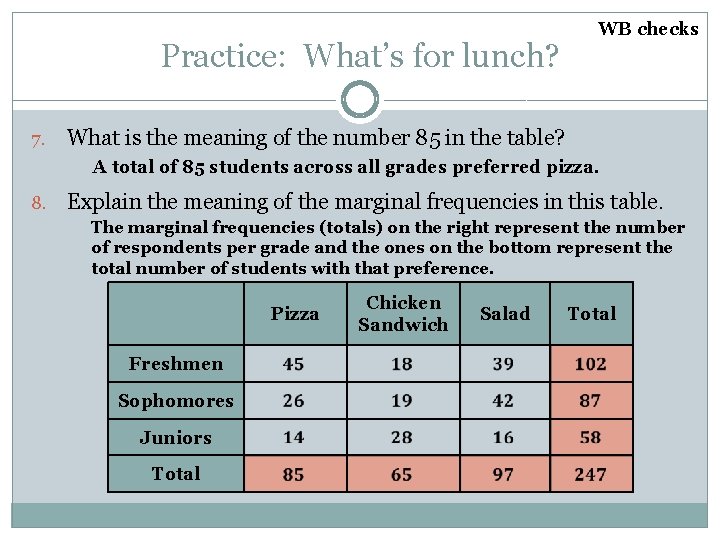
WB checks Practice: What’s for lunch? A total of 247 students were surveyed about what they liked best for lunch. The results can be shown in a two-way frequency table. Fill in the table. Begin with the grand total, then total juniors, then freshmen pizza. Pizza Freshmen Salad Chicken Sandwich Total Sophomores Juniors Total

Practice: What’s for lunch? WB checks 14 How many juniors preferred pizza? Pizza 2. What was preferred by most freshmen? Salad 3. What was preferred least by sophomores? 4. Overall, what was the most popular choice? Chicken sandwich 1. Pizza Freshmen Sophomores Juniors Total Salad Chicken Sandwich Total

WB checks Practice: What’s for lunch? 5. Were the different grade levels equally represented? No, there were 100 freshman and only 58 juniors. 6. What was the meaning of the number 28 in the table? 28 juniors preferred chicken sandwiches. Pizza Freshmen Sophomores Juniors Total Chicken Sandwich Salad Total
Practice: What’s for lunch? 7. WB checks What is the meaning of the number 85 in the table? A total of 85 students across all grades preferred pizza. 8. Explain the meaning of the marginal frequencies in this table. The marginal frequencies (totals) on the right represent the number of respondents per grade and the ones on the bottom represent the total number of students with that preference. Pizza Freshmen Sophomores Juniors Total Chicken Sandwich Salad Total
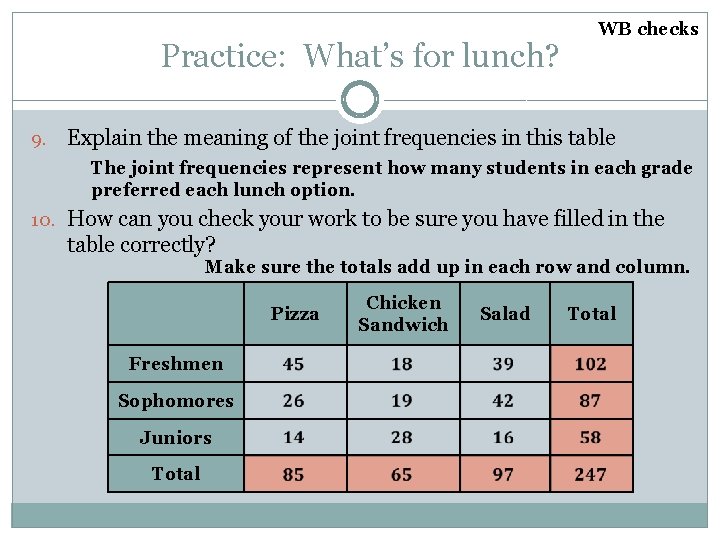
Practice: What’s for lunch? 9. WB checks Explain the meaning of the joint frequencies in this table The joint frequencies represent how many students in each grade preferred each lunch option. 10. How can you check your work to be sure you have filled in the table correctly? Make sure the totals add up in each row and column. Pizza Freshmen Sophomores Juniors Total Chicken Sandwich Salad Total

Practice: What’s for lunch? WB checks 11. Make a two way relative frequency table of the data Pizza Freshmen Sophomores Juniors Total Chicken Sandwich Salad Total

Summary How can we represent information?
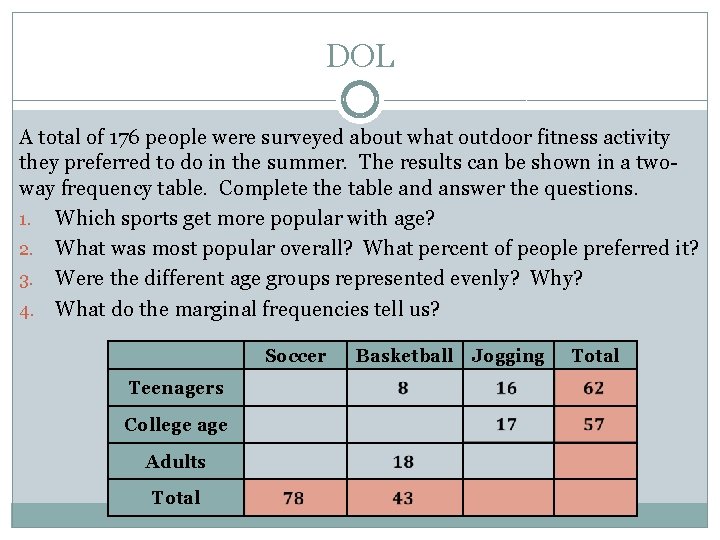
DOL A total of 176 people were surveyed about what outdoor fitness activity they preferred to do in the summer. The results can be shown in a twoway frequency table. Complete the table and answer the questions. 1. Which sports get more popular with age? 2. What was most popular overall? What percent of people preferred it? 3. Were the different age groups represented evenly? Why? 4. What do the marginal frequencies tell us? Soccer Teenagers College age Adults Total Basketball Jogging Total

DOL 1. Which sports get more popular with age? Basketball and jogging get more popular with age. 2. What was most popular overall? What percent of people preferred it? Soccer is most popular overall. 44% of respondents prefer it. Soccer Teenagers College age Adults Total Basketball Jogging Total
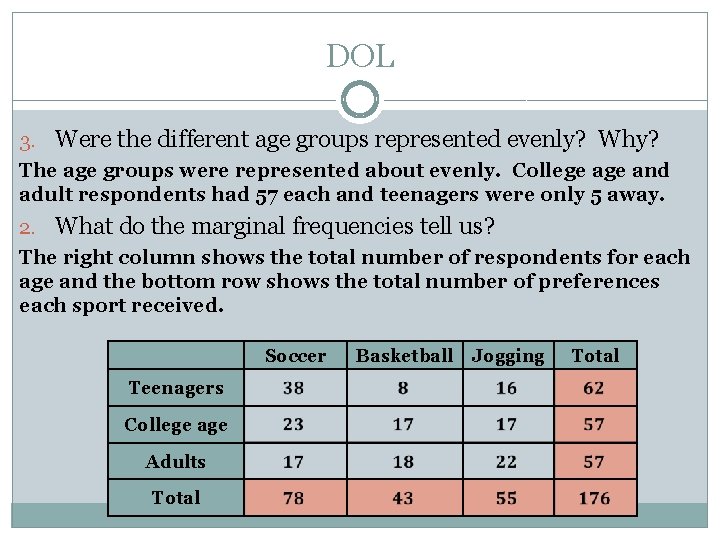
DOL 3. Were the different age groups represented evenly? Why? The age groups were represented about evenly. College and adult respondents had 57 each and teenagers were only 5 away. 2. What do the marginal frequencies tell us? The right column shows the total number of respondents for each age and the bottom row shows the total number of preferences each sport received. Soccer Teenagers College age Adults Total Basketball Jogging Total
- Slides: 49