6 6 Solving Inequalities Involving Absolute Value Algebra

6 -6 Solving Inequalities Involving Absolute Value Algebra 1 Glencoe Mc. Graw-Hill Linda Stamper

GO LA

An “AND” type of compound inequality will graph as. . An “OR” type of compound inequality will graph as. . Which type of compound inequality, “AND” or “OR”, has a greater number of solutions? Why? “Or” because it graphs as opposite rays that continue to infinity.

An absolute-value inequality is an inequality that has one of these forms: When the absolute value is on the left, the Less than symbol represents the “AND” type of inequality. It graphs as a line segment and has less – fewer solutions. I should copy the above notes in my notebook! When the absolute value is on the left, the Greater than symbol represents the “OR” type of inequality. It graphs as two opposite rays and has a greater number of solutions.

Identify the inequality as an “AND” type or “OR” type. Then identify the graph as a line segment or opposite rays. GO Inequality Type Graph OR opposite rays LA AND line segment GO OR opposite rays BEFORE you identify the type of compound inequality you must isolate the absolute value.

An absolute-value inequality is an inequality that has one of these forms: “AND” type “OR” type To solve an absolute-value inequality, write the two related inequalities – a positive inequality and a negative inequality. When you write the related inequality for the negative value, reverse the inequality symbol.

Solve. Then graph the solution. Write the inequality. Isolate the absolute value on one side of the inequality sign. Write the positive related inequality. Dorelated not identify Write the negative the type of inequality; inequality until Solve each inequality. the absolute is isolated! Write as a single value inequality. Graph. / < LA and O – 7 O – 5

Solve. Then graph the solution. Write the inequality. Isolate the absolute value on one side of the inequality sign. Write the positive related inequality. Dorelated not identify Write the negative the type of inequality; Solve. Graph. inequality until the absolute value is isolated! I should copy the above notes in my notebook! / < O – 7 O – 5 LA

Solve. Then graph the solution. Write the inequality. Isolate the absolute value on one side of the inequality sign. Write the positive related inequality. Write the negative related inequality; Solve each inequality. Reposition. Graph. / > GO or O – 7 O – 5

Solve. Then graph the solution. Example 1 Example 2

Solve. Then graph the solution. Example 1 LA • • LA – 4 • 4 Note: Less than symbol represents the “AND” type of inequality and will graph as a line segment.

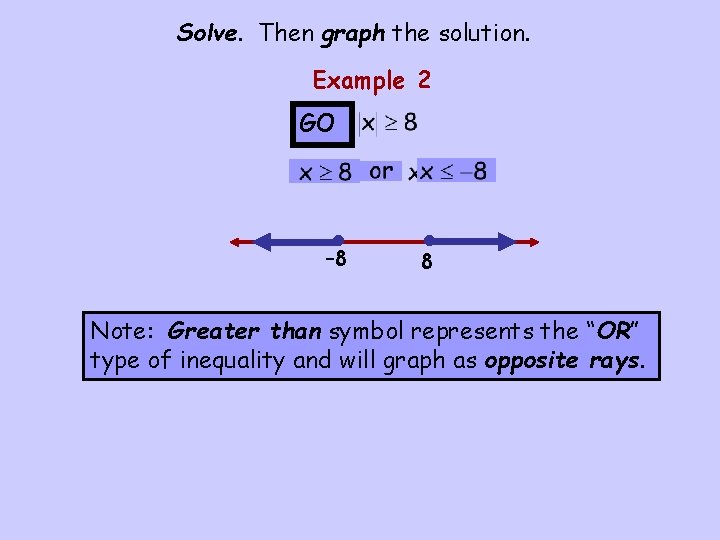
Solve. Then graph the solution. Example 2 GO • – 8 • 8 Note: Greater than symbol represents the “OR” type of inequality and will graph as opposite rays.

Solve. Then graph the solution. Absolute value cannot be less than zero (cannot be negative)! Thus there are no values that will be less than negative one.

Solve. Then graph the solution. all real numbers • 0 Absolute value will be zero or greater (it cannot be negative). Thus x can be any real number and the absolute value will be greater than negative one.

Solve. Then graph the solution. Example 3 Example 4 Example 5 Example 6 Example 7 Example 8 Example 9

Example 3 Solve. Then graph the solution. GO • 8 • 10 Note: Greater than symbol represents the “OR” type of inequality and will graph as opposite rays.

Example 4 Solve. Then graph the solution. Isolate the absolute value on one side of the inequality sign. GO O – 1 O 7

Example 5 Solve. Then graph the solution. Absolute value cannot be less than zero (cannot be negative)! Thus there are no values that will be less than negative one.

Example 6 Solve. Then graph the solution. / < • – 5 • – 1 LA

Example 7 Solve. Then graph the solution. LA • • 2

Example 8 Solve. Then graph the solution. all real numbers • 0 Absolute value will be zero or greater (it cannot be negative). Thus x can be any real number and the absolute value will be greater than negative one.

Example 9 Solve and then graph. GO • • 12

When solving an absolute-value inequality: The less than symbol represents the “AND” type of inequality. It graphs as a line segment and has less (fewer) solutions. The greater than symbol represents the “OR” type of inequality. It graphs as two opposite rays and has a greater number of solutions. GO LA

6 -A 12 Pages 332 -333 # 8– 16, 23– 26, 46 -51.