Section 5 1 Verifying Trigonometric Identities Guidelines for

















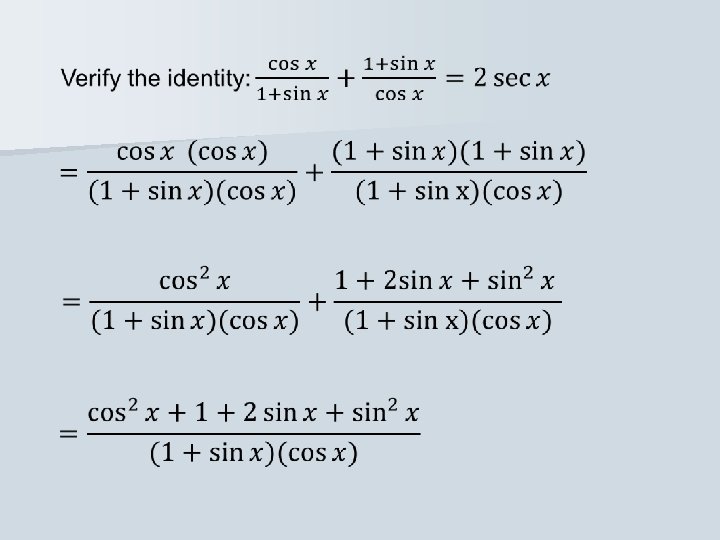


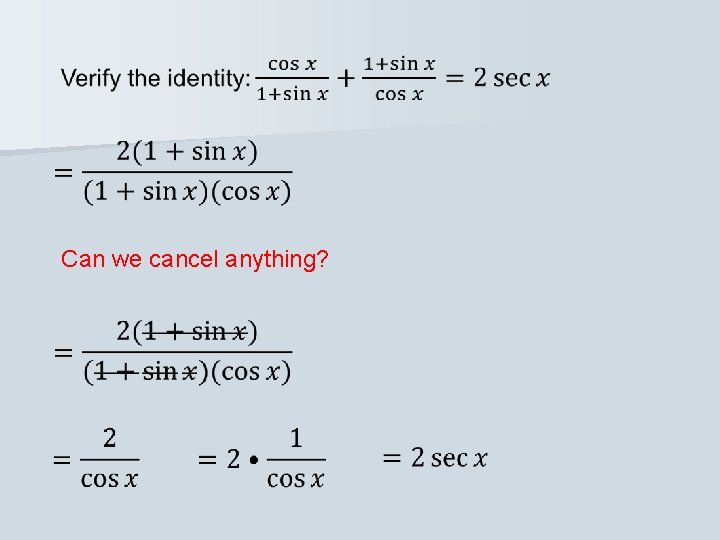





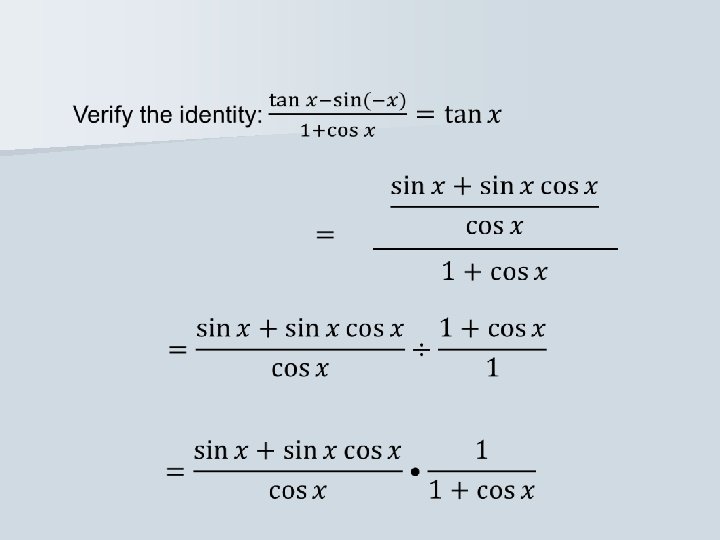



- Slides: 34

Section 5. 1 Verifying Trigonometric Identities


Guidelines for Verifying Trigonometric Identities


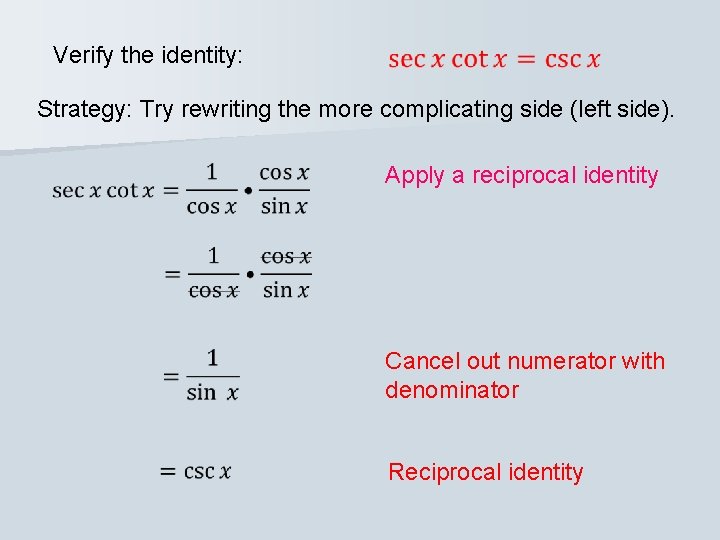
Verify the identity: Strategy: Try rewriting the more complicating side (left side). Apply a reciprocal identity Cancel out numerator with denominator Reciprocal identity

Verify the identity: Strategy: Try rewriting the more complicating side (left side). Apply a reciprocal identity Cancel out numerator with denominator Reciprocal identity


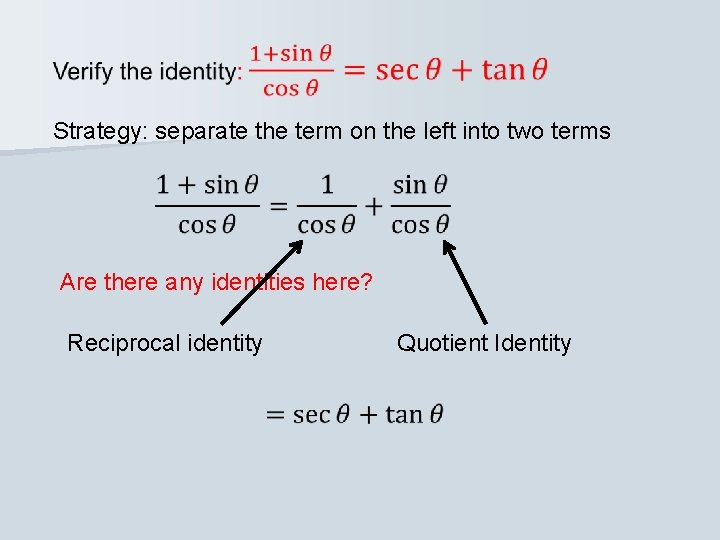
Verify the identity: Strategy: Try rewriting the more complicating side, the left side, using identities that contain sine and cosine. Apply a quotient identity Multiply

Verify the identity: Continued from previous slide… Get a common denominator, which is Multiply

Verify the identity: Continued from previous slide… Add the numerators Do you recognize an identity? Pythagorean Identity

Verify the identity: Continued from previous slide… Do you recognize a identity?

Verify the identity: Strategy: Try rewriting the more complicating side, the left side, using identities that contain sine and cosine. Apply a quotient identity Multiply

Verify the identity: Continued from previous slide… Get a common denominator, which is Multiply

Verify the identity: Continued from previous slide… Add the numerators Do you recognize an identity?

Verify the identity: Continued from previous slide… Do you recognize a identity?

Strategy: start with the more complicated side, the left side. Is there a greatest common factor? Is there a variation of an identity here? Multiply

Strategy: start with the more complicated side, the left side. Is there a greatest common factor? Is there a variation of an identity here? Multiply

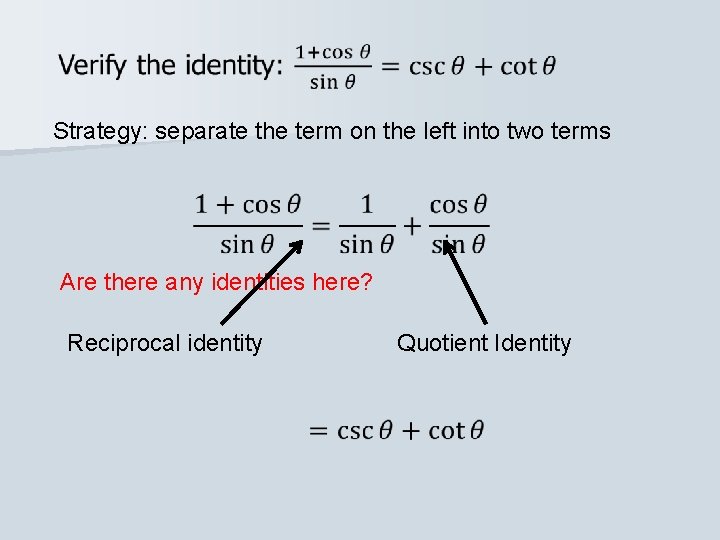
Strategy: separate the term on the left into two terms Are there any identities here? Reciprocal identity Quotient Identity

Strategy: separate the term on the left into two terms Are there any identities here? Reciprocal identity Quotient Identity

Strategy: start with the more complicated side, the left side. What must we do to add the two fractions on the left? Find the least common denominator, which is…
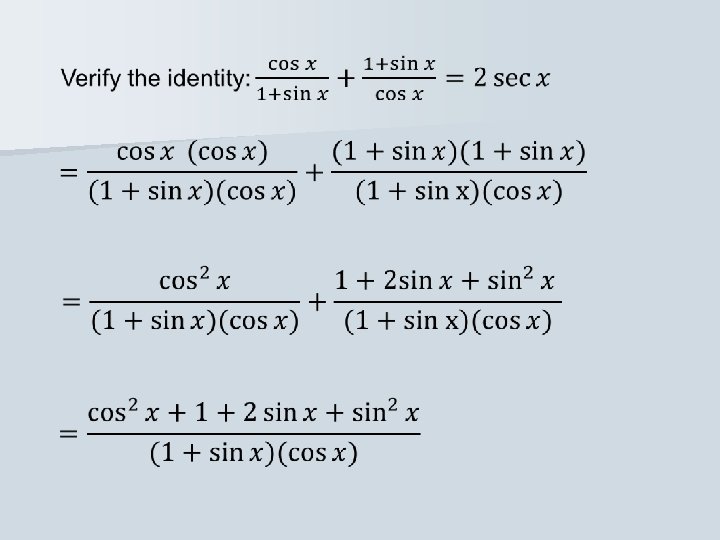

Do you see an identity? Pythagorean Identity

Can we find a greatest common factor in the numerator?
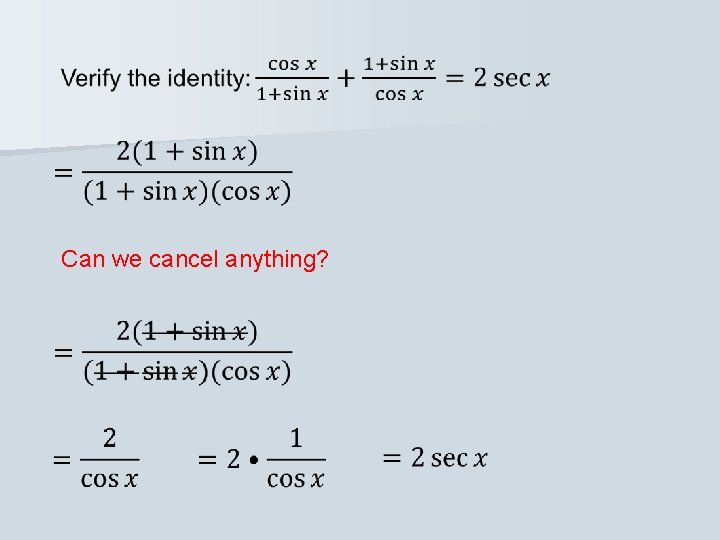
Can we cancel anything?

Strategy: Both sides are equally complicated. Everything is expressed in sines and cosines. Let’s work on the left side to make it look like the right. Do you see an identity?

What do we know about sin(-x)?

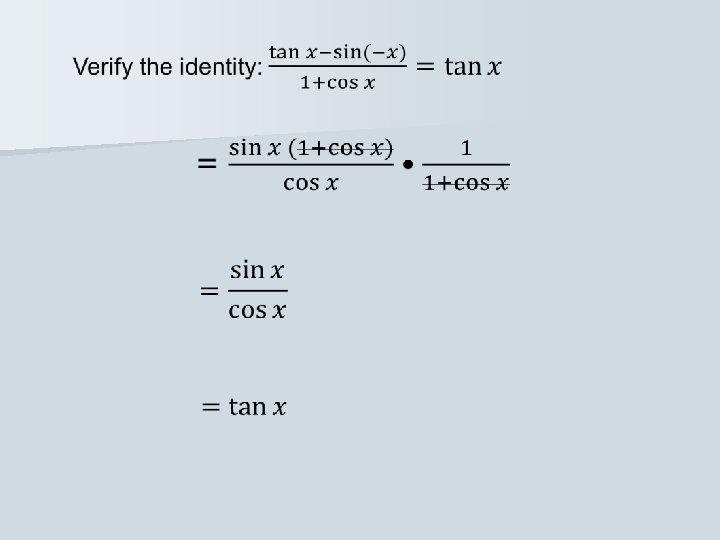
Do you see an identity? Quotient identity

We need to find the least common denominator in the numerator.

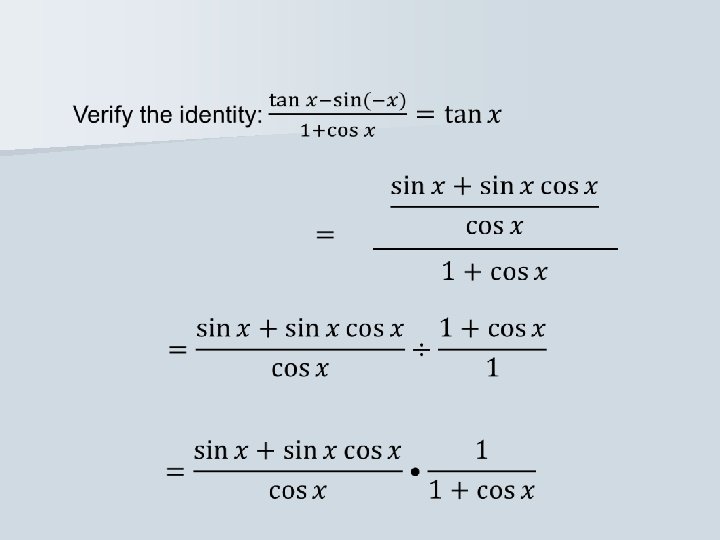

How about a common factor in the numerator?


Verifying Trig Functions Review 1. 2. 3. 4. 5. 6. Learn the fundamental identities. Try to rewrite the more complicated side of the equation so that it is identical to the simpler side. It is often helpful to express all functions in terms of sine and cosine and then simplify the result. Usually, any factoring or indicated algebraic operations should be performed. For example, As you select substitutions, keep in mind the side you are not changing, because it represents your goal. If an expression contains 1 + sin x, multiplying both numerator and denominator by 1 – sin x would give 1 – sin² x, which could be replaced with cos² x. Copyright © 2007 Pearson Education, Inc. Slide 9 -33
