Solving Absolute Value Equations Inequalities Recall Absolute value

Solving Absolute Value Equations & Inequalities

Recall : Absolute value | x | : is the distance between x and 0. If | x | = 8, then – 8 and 8 is a solution of the equation ; or | x | 8, then any number between 8 and 8 is a solution of the inequality.

Absolute Value (of x) • • Symbol lxl The distance x is from 0 on the number line. Always positive Ex: l-3 l=3 -4 -3 -2 -1 0 1 2 Recall: You can solve some absolute-value equations using mental math. For instance, you learned that the equation | x | 3 has two solutions: 3 and 3. To solve absolute-value equations, you can use the fact that the expression inside the absolute value symbols can be either positive or negative.

Solving an Absolute-Value Equation: Solve | x 2 | 5 Solve | 2 x 7 | 5 4

Answer : : Solving an Absolute-Value Equation Solve | x 2 | 5 The expression x 2 can be equal to 5 or 5. x 2 IS POSITIVE |x 2| 5 x 2 5 x 7 x 2 IS NEGATIVE |x 2| 5 x 2 5 x 3 The equation has two solutions: 7 and – 3. CHECK | 7 2 | | 5 | 3 2 | | 5 | 5

Answer : : Solve | 2 x 7 | 5 4 SOLUTION Isolate the absolute value expression on one side of the equation. 2 x 7 IS POSITIVE 2 x 2 x 77 IS IS NEGATIVE | 2 x 7 | 5 4 || 2 x 2 x 77 || 55 44 | 2 x 7 | 9 2 x 7 +9 || 2 x 2 x 77 || 99 2 x 2 x 9 2 x 77 7 9 9 2 x 16 x 8 2 x 2 x 2 2 TWO SOLUTIONS x 1

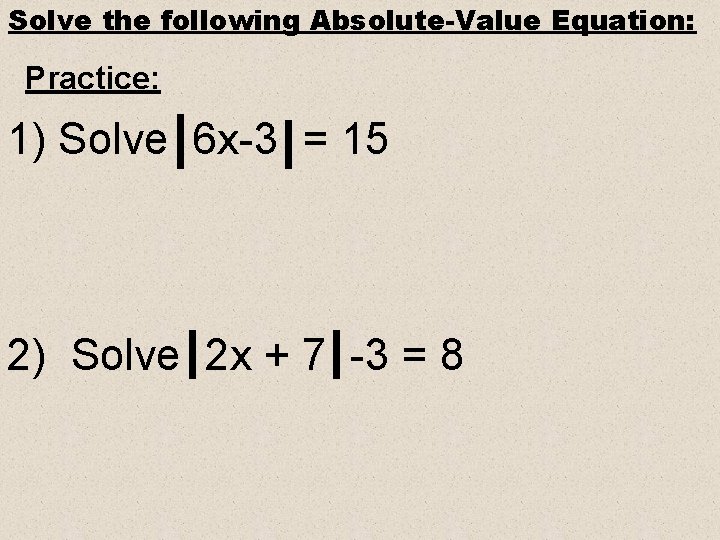
Solve the following Absolute-Value Equation: Practice: 1) Solve 6 x-3 = 15 2) Solve 2 x + 7 -3 = 8

Answer : : 1) Solve 6 x-3 = 15 or 6 x = 18 or x = 3 or 6 x-3 = -15 6 x = -12 x = -2 * Plug in answers to check your solutions!

Answer : : 2) Solve 2 x + 7 -3 = 8 Get the abs. value part by itself first! 2 x+7 = 11 Now split into 2 parts. 2 x+7 = 11 or 2 x+7 = -11 2 x = 4 or 2 x = -18 x = 2 or x = -9 Check the solutions.

***Important NOTE*** 3 2 x + 9 +12 = 10 - 12 u l o n o ti S No 3 2 x + 9 = - 2 3 What about this absolute value equation? 3 x – 6 – 5 = – 7

g n s i e h i t p i l a r a u G q & e n g I n e i v u l l a o S te V u l o s Ab

Solving an Absolute Value Inequality: ● Step 1: Rewrite the inequality as a conjunction or a disjunction. ● If you have a you are working with a conjunction or an ‘and’ statement. Remember: “Less thand” ● If you have a you are working with a disjunction or an ‘or’ statement. Remember: “Greator” ● Step 2: In the second equation you must negate the right hand side and reverse the direction of the inequality sign. ● Solve as a compound inequality.

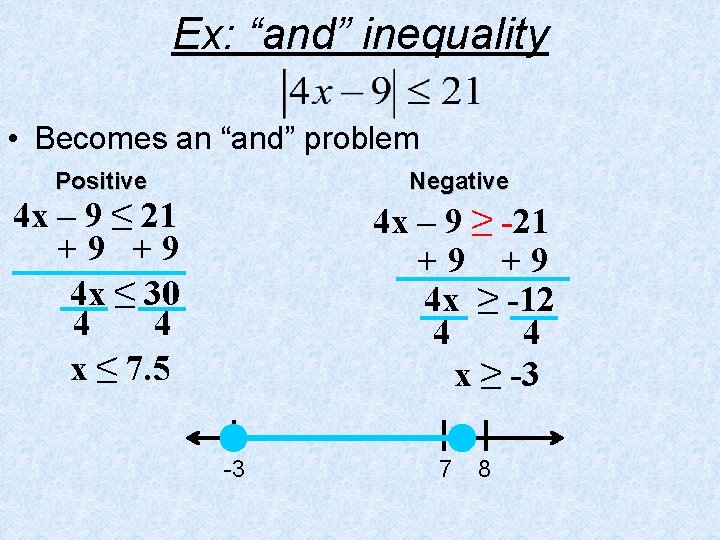
Ex: “and” inequality • Becomes an “and” problem Positive Negative 4 x – 9 ≤ 21 +9 +9 4 x ≤ 30 4 4 x ≤ 7. 5 4 x – 9 ≥ -21 +9 +9 4 x ≥ -12 4 4 x ≥ -3 -3 7 8

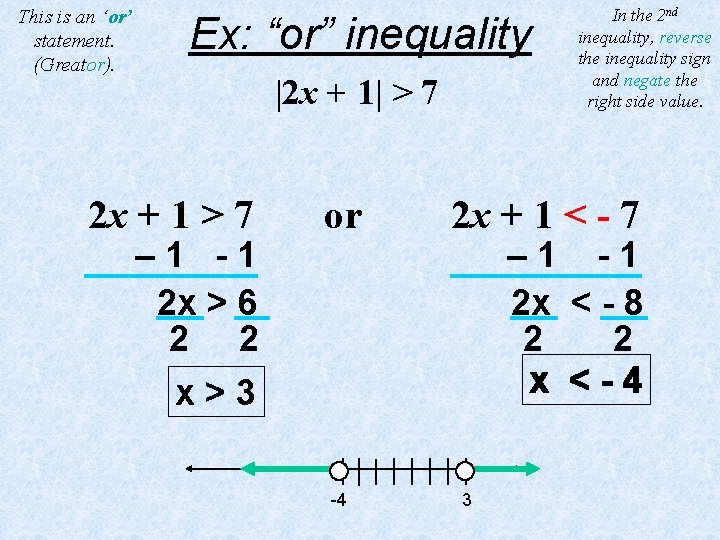
This is an ‘or’ statement. (Greator). Ex: “or” inequality |2 x + 1| > 7 2 x + 1 > 7 – 1 -1 2 x > 6 2 2 x>3 or -4 In the 2 nd inequality, reverse the inequality sign and negate the right side value. 2 x + 1 < - 7 – 1 -1 2 x < - 8 2 2 x <-4 3

Solving Absolute Value Inequalities: Solve | x 4 | < 3 and graph the solution. Solve | 2 x 1 | 3 6 and graph the solution.

Answer : : Solve | x 4 | < 3 x 4 IS POSITIVE |x 4| 3 x 4 IS NEGATIVE |x 4| 3 x 4 3 x 7 x 1 Reverse inequality symbol. The solution is all real numbers greater than 1 and less than 7. This can be written as 1 x 7.

Answer : : Solve | 2 x 1 | 3 6 and graph the solution. 2 x + 1 IS POSITIVE | 2 x 1 | 3 6 2 x + 1 IS NEGATIVE | 2 x 1 | 3 6 | 2 x 1 | 9 2 x 1 +9 2 x 1 9 Reverse inequality symbol. 2 x 10 2 x 8 x 4 x 5 The solution is all real numbers greater than or equal to 4 or less than or equal to 5. This can be written as the compound inequality x 5 or x 4. 6 5 4 3 2 1 0 1 2 3 4 5 6

Solve and graph the following Absolute-Value Inequalities: 3) 4) |x -5| < 3

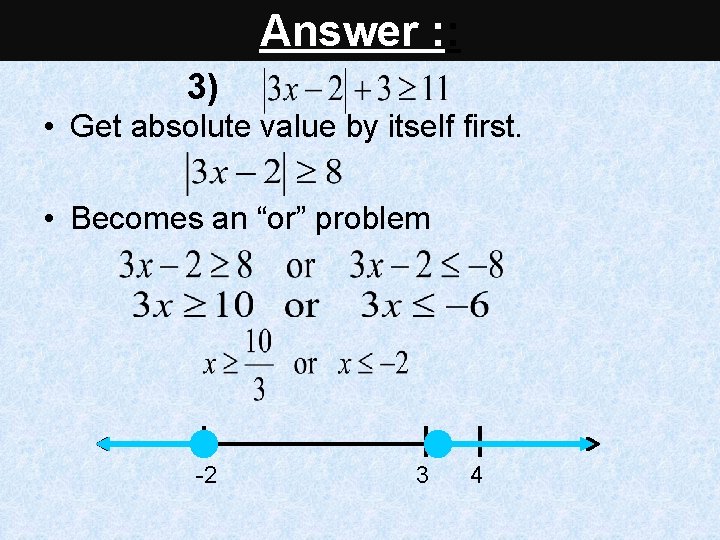
Solve Answer & graph. : : 3) • Get absolute value by itself first. • Becomes an “or” problem -2 3 4

Answer : : This is an ‘and’ statement. (Less thand). 4) |x -5|< 3 x -5< 3 and x -5> -3 x < 8 and x > 2 2<x<8 2 Rewrite. In the 2 nd inequality, reverse the inequality sign and negate the right side value. Solve each inequality. Graph the solution. 8

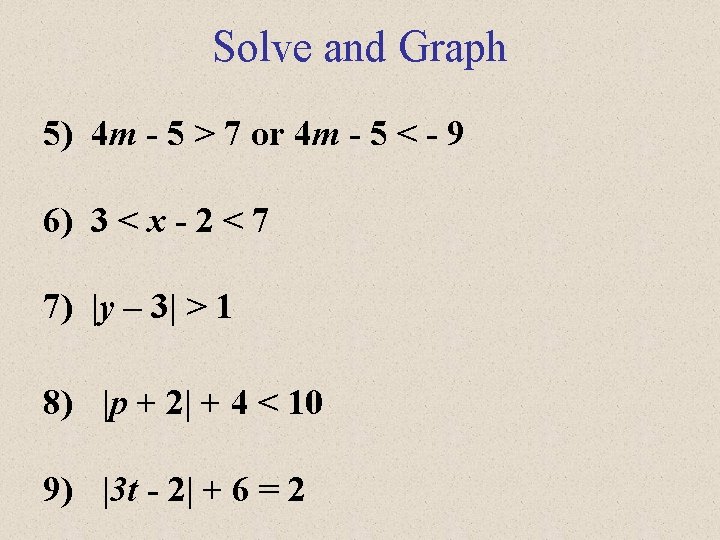
Solve and Graph 5) 4 m - 5 > 7 or 4 m - 5 < - 9 6) 3 < x - 2 < 7 7) |y – 3| > 1 8) |p + 2| + 4 < 10 9) |3 t - 2| + 6 = 2