Trigonometric Identities A trigonometric equation is an equation

Trigonometric Identities A trigonometric equation is an equation that involves at least one trigonometric function of a variable. The equation is a trigonometric identity if it is true for all values of the variable for which both sides of the equation are defined. Recall the basic trig identities: Prove that L. S. = R. S.

Trigonometric Identities Quotient Identities Reciprocal Identities Pythagorean Identities sin 2 q + cos 2 q = 1 tan 2 q + 1 = sec 2 q cot 2 q + 1 = csc 2 q sin 2 q = 1 - cos 2 q = 1 - sin 2 q tan 2 q = sec 2 q - 1 cot 2 q = csc 2 q - 1

Trigonometric Identities [cont’d] sinx x sinx = sin 2 x = cos. A

Simplifying Trigonometric Expressions Identities can be used to simplify trigonometric expressions. Simplify. a) b)

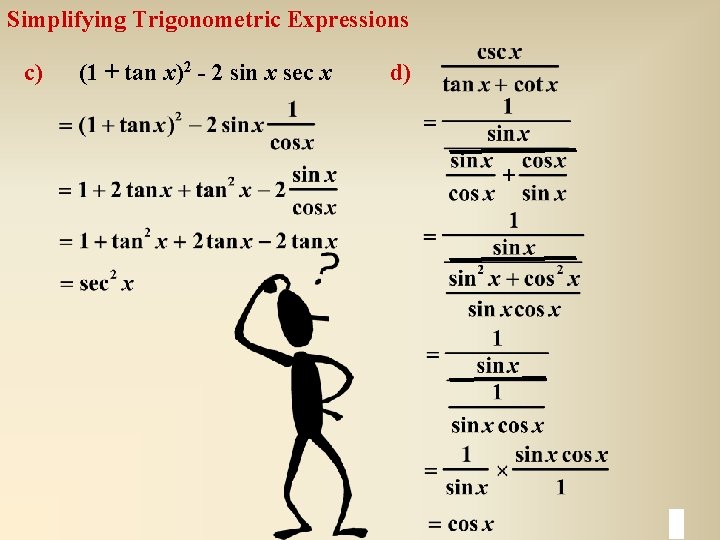
Simplifying Trigonometric Expressions c) (1 + tan x)2 - 2 sin x sec x d)

Proving an Identity Steps in Proving Identities 1. Start with the more complex side of the identity and work with it exclusively to transform the expression into the simpler side of the identity. 2. Look for algebraic simplifications: • Do any multiplying , factoring, or squaring which is obvious in the expression. • Reduce two terms to one, either add two terms or factor so that you may reduce. 3. Look for trigonometric simplifications: • Look for familiar trig relationships. • If the expression contains squared terms, think of the Pythagorean Identities. • Transform each term to sine or cosine, if the expression cannot be simplified easily using other ratios. 4. Keep the simpler side of the identity in mind.

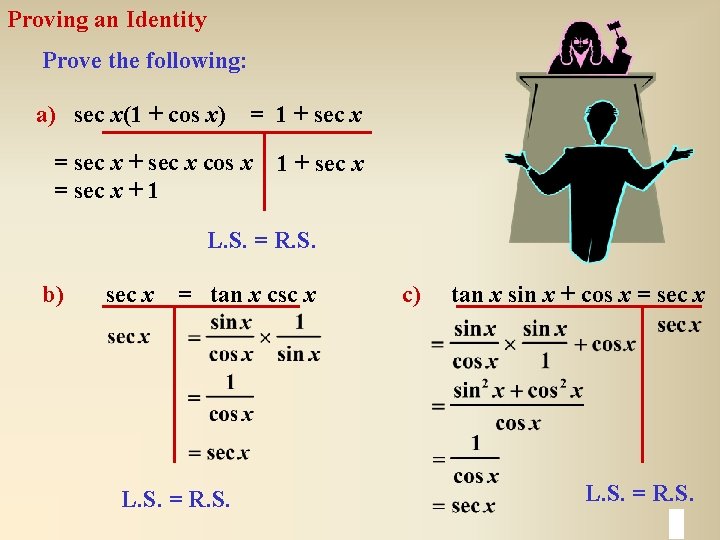
Proving an Identity Prove the following: a) sec x(1 + cos x) = 1 + sec x = sec x + sec x cos x = sec x + 1 1 + sec x L. S. = R. S. b) sec x = tan x csc x L. S. = R. S. c) tan x sin x + cos x = sec x L. S. = R. S.

Proving an Identity d) sin 4 x - cos 4 x = 1 - 2 cos 2 x = (sin 2 x - cos 2 x)(sin 2 x + cos 2 x) 1 - 2 cos 2 x = (1 - cos 2 x) = 1 - 2 cos 2 x L. S. = R. S. e) L. S. = R. S.

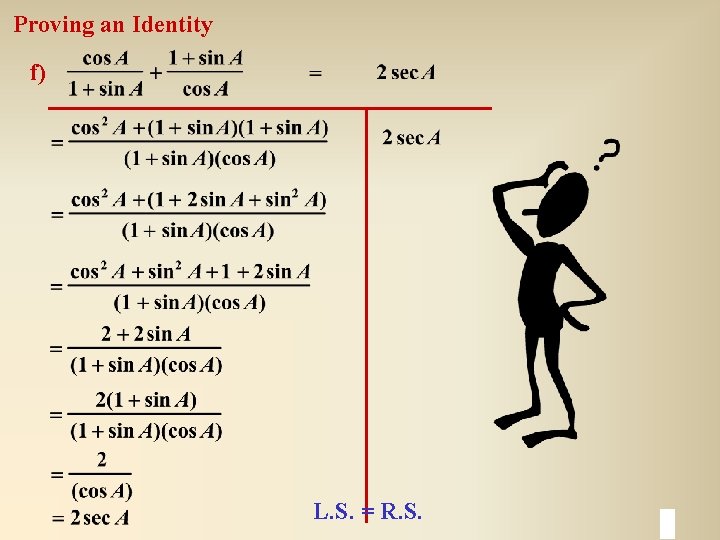
Proving an Identity f) L. S. = R. S.

Using Exact Values to Prove an Identity Consider a) Use a graph to verify that the equation is an identity. b) Verify that this statement is true for x = c) Use an algebraic approach to prove that the identity is true in general. State any restrictions. a)

Using Exact Values to Prove an Identity [cont’d] b) Verify that this statement is true for x = Rationalize the denominator: L. S. = R. S. Therefore, the identity is true for the particular case of

Using Exact Values to Prove an Identity [cont’d] c) Use an algebraic approach to prove that the identity is true in general. State any restrictions. Restrictions: Note the left side of the equation has the restriction 1 - cos x ≠ 0 or cos x ≠ 1. Therefore, x ≠ 0 + 2 p n, where n is any integer. The right side of the equation has the restriction sin x ≠ 0. x = 0 and p Therefore, x ≠ 0 + 2 pn and x ≠ p + 2 pn, where n is any integer. L. S. = R. S.

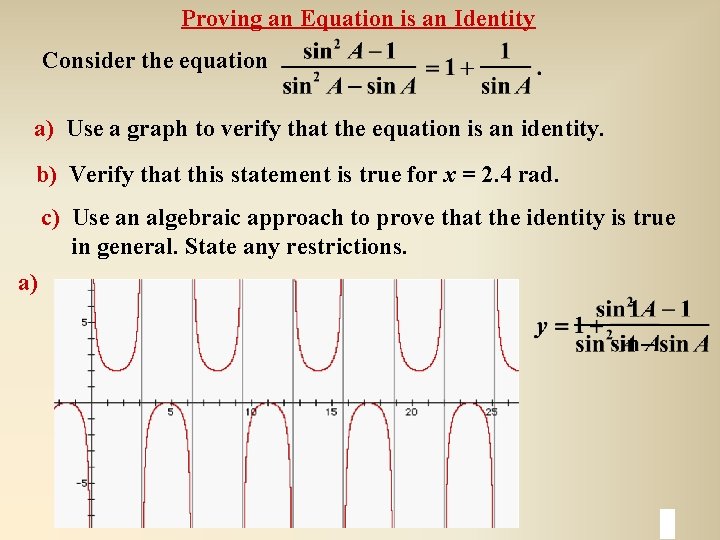
Proving an Equation is an Identity Consider the equation a) Use a graph to verify that the equation is an identity. b) Verify that this statement is true for x = 2. 4 rad. c) Use an algebraic approach to prove that the identity is true in general. State any restrictions. a)

Proving an Equation is an Identity [cont’d] b) Verify that this statement is true for x = 2. 4 rad. = 2. 480 466 L. S. = R. S. Therefore, the equation is true for x = 2. 4 rad.

Proving an Equation is an Identity [cont’d] c) Use an algebraic approach to prove that the identity is true in general. State any restrictions. Note the left side of the equation has the restriction: sin 2 A - sin A ≠ 0 sin A(sin A - 1) ≠ 0 sin A ≠ 0 or sin A ≠ 1 L. S. = R. S. The right side of the equation has the restriction sin A ≠ 0, or A ≠ 0. Therefore, A ≠ 0, p + 2 p n, where n is any integer.