Parallel Lines and Angles Vertical Angles Vertical Angles

Parallel Lines and Angles

Vertical Angles • Vertical Angles are angles that are opposite each other at an intersection. • Vertical Angles are equal 1 2 3 4 Angles 1 and 4 are vertical angles Angles 2 and 3 are vertical angles On your notesheet: Write a word and a picture definition for vertical angles.

Supplementary Angles • Supplementary angles are angles that form lines (also called linear pairs) • Supplementary angles add up to 180 1 2 3 4 Angles 1 and 2 are supplementary, Angles 1 and 3 are supplementary Angles 2 and 4 are supplementary, Angles 3 and 4 are supplementary On your notesheet: Write a word and a picture definition for supplementary angles.

Parallel Lines and Planes You will learn to describe relationships among lines, parts of lines, and planes. In geometry, two lines in a plane that are always the same parallel lines distance apart are ______. No two parallel lines intersect, no matter how far you extend them.

Parallel Lines and Planes Definition of Parallel Lines Two lines are parallel if they are in the same plane and intersect do not ____. -This means the lines never touch -This means the lines have the same slope -This means the lines are always the same distance apart -The symbol for parallel is two vertical lines (II). For example if line m and line t are parallel you could write m II t. On your notesheet: Write a verbal and picture definition of parallel lines On your paper: #1. What are three ways to describe how lines are parallel? #2. What is the symbol for parallel?

Parallel Lines and Transversals You will learn to identify the relationships among pairs of interior and exterior angles formed by two parallel lines and a transversal.

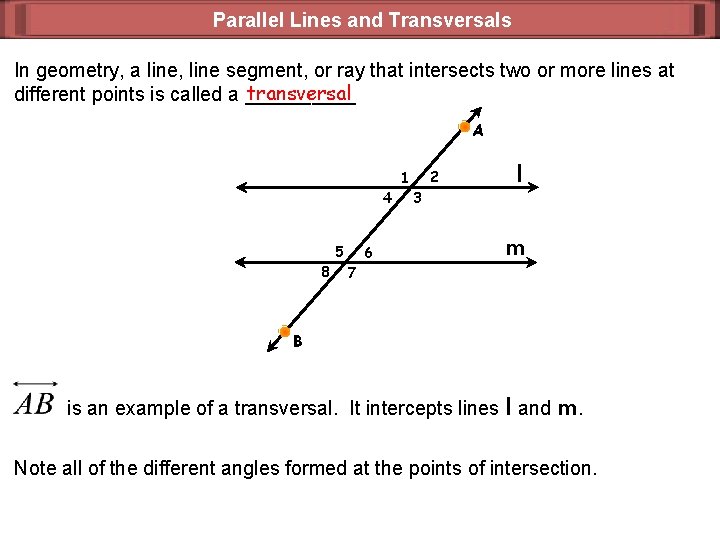
Parallel Lines and Transversals In geometry, a line, line segment, or ray that intersects two or more lines at transversal different points is called a _____ A 2 1 4 5 8 6 7 3 l m B is an example of a transversal. It intercepts lines l and m. Note all of the different angles formed at the points of intersection.

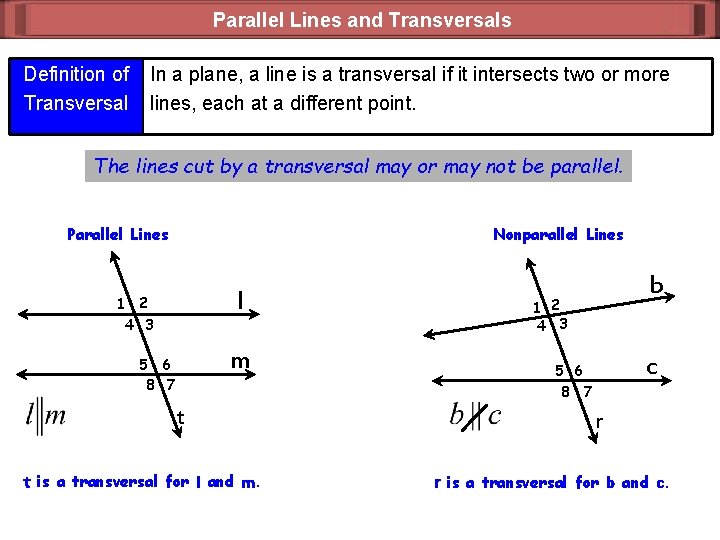
Parallel Lines and Transversals Definition of Transversal In a plane, a line is a transversal if it intersects two or more lines, each at a different point. The lines cut by a transversal may or may not be parallel. Parallel Lines Nonparallel Lines l 1 2 4 3 m 5 6 8 7 is a transversal for l and m. c 5 6 8 7 t t b r r is a transversal for b and c.

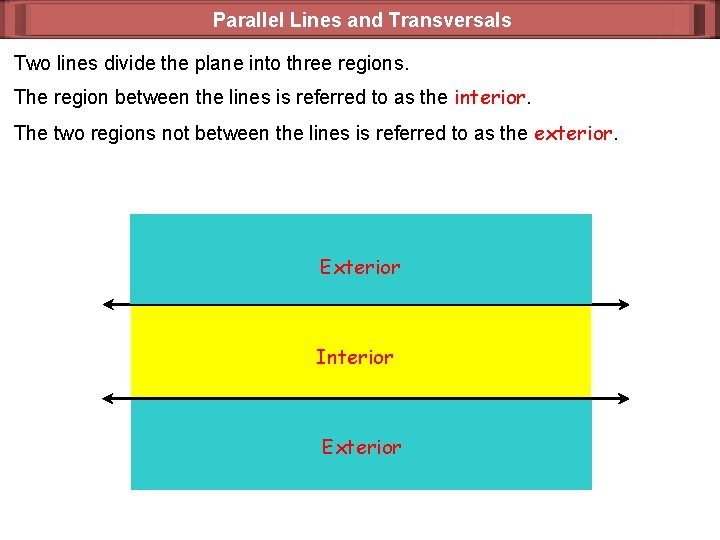
Parallel Lines and Transversals Two lines divide the plane into three regions. The region between the lines is referred to as the interior. The two regions not between the lines is referred to as the exterior. Exterior Interior Exterior

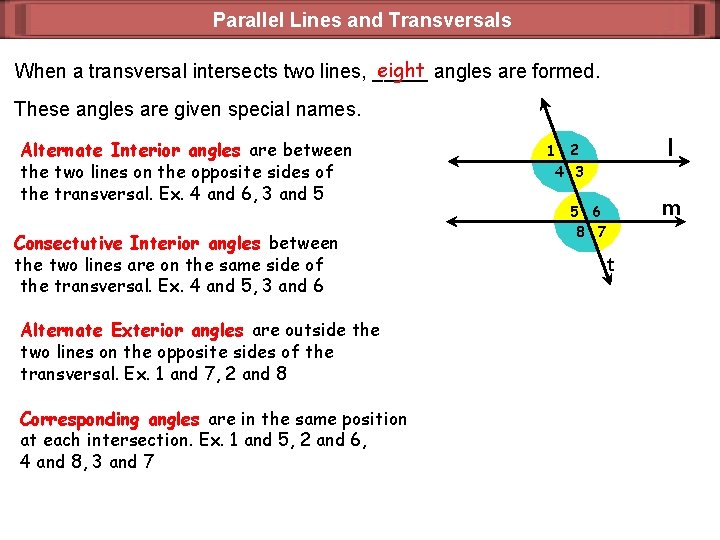
Parallel Lines and Transversals eight angles are formed. When a transversal intersects two lines, _____ These angles are given special names. Alternate Interior angles are between the two lines on the opposite sides of the transversal. Ex. 4 and 6, 3 and 5 Consectutive Interior angles between the two lines are on the same side of the transversal. Ex. 4 and 5, 3 and 6 Alternate Exterior angles are outside the two lines on the opposite sides of the transversal. Ex. 1 and 7, 2 and 8 Corresponding angles are in the same position at each intersection. Ex. 1 and 5, 2 and 6, 4 and 8, 3 and 7 l 1 2 4 3 m 5 6 8 7 t

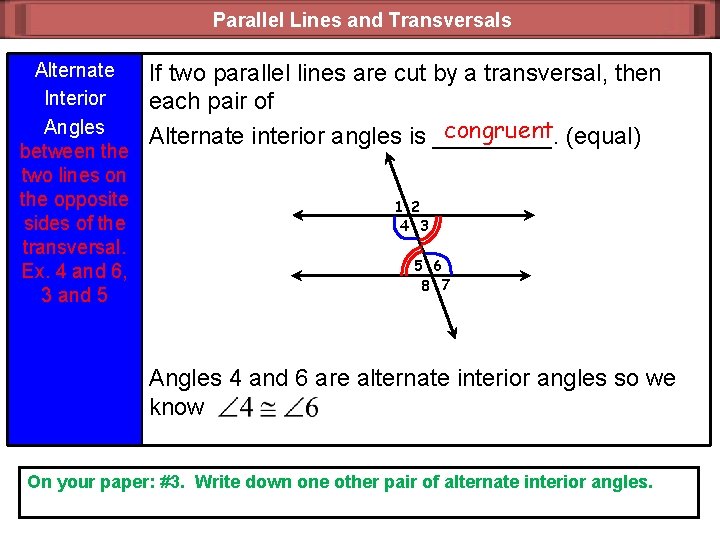
Parallel Lines and Transversals Alternate Interior Angles between the two lines on the opposite sides of the transversal. Ex. 4 and 6, 3 and 5 If two parallel lines are cut by a transversal, then each pair of congruent (equal) Alternate interior angles is _____. 1 2 4 3 5 6 8 7 Angles 4 and 6 are alternate interior angles so we know On your paper: #3. Write down one other pair of alternate interior angles.

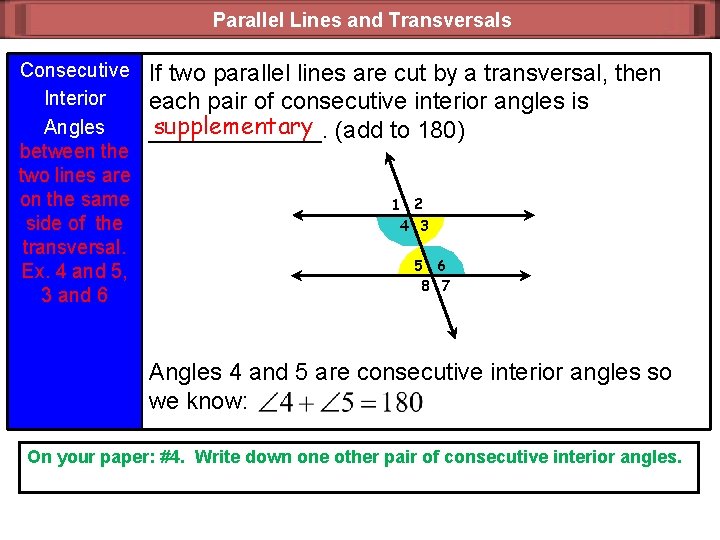
Parallel Lines and Transversals Consecutive Interior Angles between the two lines are on the same side of the transversal. Ex. 4 and 5, 3 and 6 If two parallel lines are cut by a transversal, then each pair of consecutive interior angles is supplementary (add to 180) _______. 1 2 4 3 5 6 8 7 Angles 4 and 5 are consecutive interior angles so we know: On your paper: #4. Write down one other pair of consecutive interior angles.

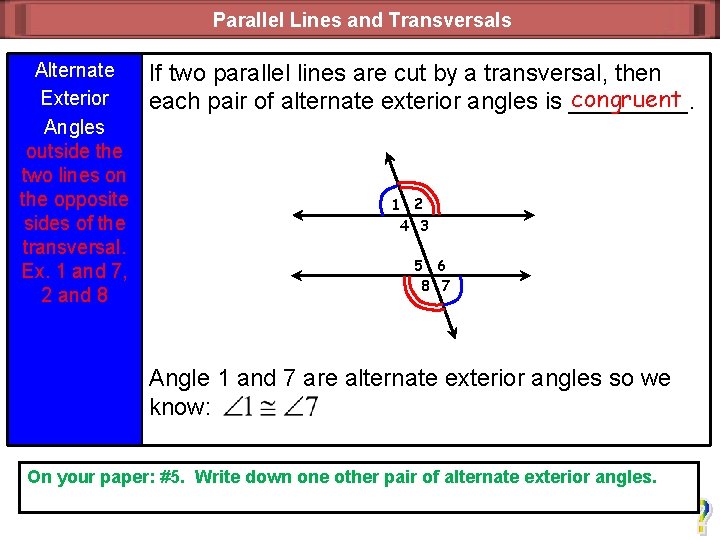
Parallel Lines and Transversals Alternate Exterior Angles outside the two lines on the opposite sides of the transversal. Ex. 1 and 7, 2 and 8 If two parallel lines are cut by a transversal, then congruent each pair of alternate exterior angles is _____. 1 2 4 3 5 6 8 7 Angle 1 and 7 are alternate exterior angles so we know: On your paper: #5. Write down one other pair of alternate exterior angles.

Parallel Lines and Transversals Corresponding Angles are in the same position at each intersection. Ex. 1 and 5, 2 and 6, 4 and 8, 3 and 7 If two parallel lines are cut by a transversal, then each pair of corresponding angles is _____. congruent l 1 2 4 3 m 5 6 8 7 t Angle 1 and 5 are both in the upper left of each intersection so they are corresponding angles and we then know angle 1=angle 5 On your paper: #6. Write down three other pairs of corresponding angles.

Transversals and Corresponding Angles Concept Summary Types of angle pairs formed when a transversal cuts two parallel lines. Congruent Supplementary alternate interior consecutive interior alternate exterior corresponding On your notesheet: Under “Special pair of Angles” for each pair write equal or supplementary, then using the examples on the notesheet write one pair from A and B. Turn in your half piece of paper. Go to a table and complete your notesheet page on parallel lines. After you have completed this, start the next sheet in your packet. Whatever you don’t complete is homework for tonight.