Vorlesung Regelungstechnik 2 Digitaler Regelkreis 30 April 2003

Vorlesung Regelungstechnik 2 Digitaler Regelkreis 30. April 2003 Hochschule für Technik und Wirtschaft des Saarlandes Fachbereich Elektrotechnik Goebenstr. 40 66117 Saarbrücken April 2003 / Regelungstechnik 2 Blatt 2. 1 Prof. Dr. -Ing. Benedikt Faupel

Regelungstechnik 2 Inhalte Vorlesung Regelungstechnik 2 Digitale Regelung • Beschreibung kontinuierlicher / digitaler Signale • Grundfunktionen von digitalen Regelkreisen • Elemente in digitalen Regelkreisen (DA-Wandler, AD-Wandler, Halteglieder) • Gleichungen, Differenzengleichungen für digitaler Regelelemente P, I, D und Kombinationen hiervon • PID-Regelalgorihtmen • Einstellregeln für digitale Regelkreise • z-Transformation und Beschreibung von digitalen Regelkreisen im Frequenzbereich • Stabilität von digitalen Regelkreisen April 2003 / Regelungstechnik 2 Blatt 2. 2 Prof. Dr. -Ing. Benedikt Faupel

Regelungstechnik 2 Inhalte Vorlesung Regelungstechnik 2 Zustandsregelung • Einführung in die Zustands(-raum)-Beschreibung • Mathematische Grundlagen (Matrizen und Rechenverfahren= • Methoden zur Berechnung von Übertragungssystemen mit Zustandsvariablen • Lösungen der. Zustandsgleichung im Zeit- und Frequenzbereich • Normalformen von Übertragungssystemen (Beobachternormalform, Regelungsnormalform) • Steuerbarkeit und Beobachtbarkeit von Übertragungssystemen • Transformationen auf Regelungs- und Beobachtungsnormalform • Regelung durch Zustandsrückführung April 2003 / Regelungstechnik 2 Blatt 2. 3 Prof. Dr. -Ing. Benedikt Faupel

Übergang vom zeitkontinuierlichen zum zeitdiskreten Signal Kontinuierliches Signal wird über Abtaster und A/D-Wandler in ein zeitdiskretes digitalisiertens Signal gewandlet x(t) -> x(k. T) April 2003 / Regelungstechnik 2 Blatt 2. 4 Prof. Dr. -Ing. Benedikt Faupel

Übergang vom zeitdiskreten zum zeitkontinuierlichen Signal Zeitdiskretes Signal wird über Halteglied und D/A-Wandler in ein kontinuierliches Signal gewandelt y(kt) -> y(t) April 2003 / Regelungstechnik 2 Blatt 2. 5 Prof. Dr. -Ing. Benedikt Faupel

Digitaler Regelkreis Im digitalen Regelkreis müssen analoge Größen digitalisiert werden. Die Regelstrecke wird meistens mit analog arbeitenden Stellgeräten beeinflusst. Hier ist entsprechend die Umwandlung der digitalen Größen in analoge Größen vorzunehmen. Digitaler Regler ermittelt nach einer Berechnungsvorschrift die Folge der Stellwerte y(k. T) aus der Folge e(k. T). April 2003 / Regelungstechnik 2 Blatt 2. 6 Prof. Dr. -Ing. Benedikt Faupel

Digitale Regelkreise Eigenschaften: • Zu regelender Prozess verläuft kontinuierlich. • Digitalregler verarbeitet diskrete Zahlenfolgen und ermittelt Stellgrößenwerte • Stellgröße arbeitet kontinuierlich. Stellgrößenwerte werden als treppenförmiges Signal aus der Stellgrößenfolge gebildet • Für Abtastzeiten Tab << Systemzeit kann digitale Regelung wie quasikontinuierliche Regelung interpretiert werden. Für diese Betrachtung keine Abtasttheorie erforderlich • Alternative Lösung digitaler Regelungen basiert auf Anwendung der z-Transformation und Lösung von Differenzengleichungen April 2003 / Regelungstechnik 2 Blatt 2. 7 Prof. Dr. -Ing. Benedikt Faupel

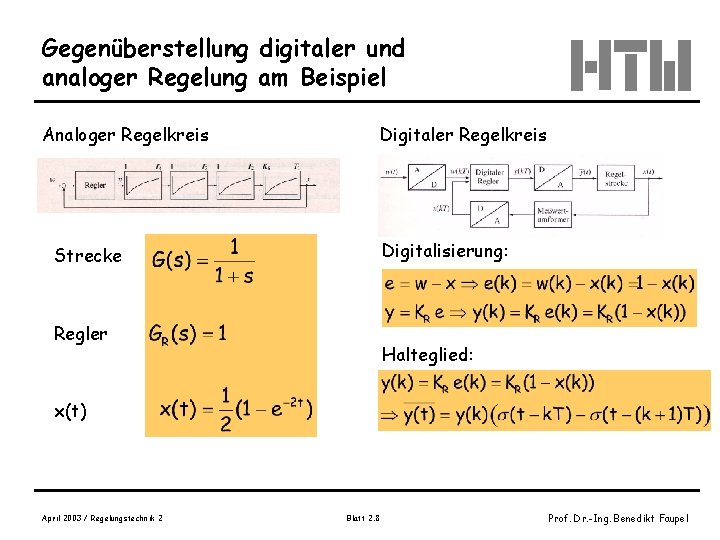
Gegenüberstellung digitaler und analoger Regelung am Beispiel Analoger Regelkreis Digitalisierung: Strecke Regler Halteglied: x(t) April 2003 / Regelungstechnik 2 Blatt 2. 8 Prof. Dr. -Ing. Benedikt Faupel

Digitaler Regelkreis Treppenförmige Stellgröße wirkt nun auf die Regelstrecke und bleibt innerhalb der Abtastzeit konstant. Allgemeine Lösung: April 2003 / Regelungstechnik 2 Blatt 2. 9 Prof. Dr. -Ing. Benedikt Faupel

Allgemeine Lösung Simulation in Matlab und Excel mit Variation der einzelnen Größen KR, Tab, TS, . . KR = 2, 5, 10, 20, . . . Unterschied analoges und digitales Verhalten April 2003 / Regelungstechnik 2 Blatt 2. 10 Prof. Dr. -Ing. Benedikt Faupel

Allgemeine Lösung ist ein iteratives Verfahren: • Bestimmen der Startwerte für y, e und x(0) • Starten der Abtastzeit für jedes Abtastintervall gilt • Ausführen des Regelalgorithmus y(k) = KR e(k) • D/A-Wandeln von y(k) zur Bestimmung der analogen Stellgröße • X(t) stellt sich entsprechend ein Für jeden neuen Abtastzeitpunkt: • Bestimmen von x(k), w(k) und e(k) April 2003 / Regelungstechnik 2 Blatt 2. 11 Prof. Dr. -Ing. Benedikt Faupel

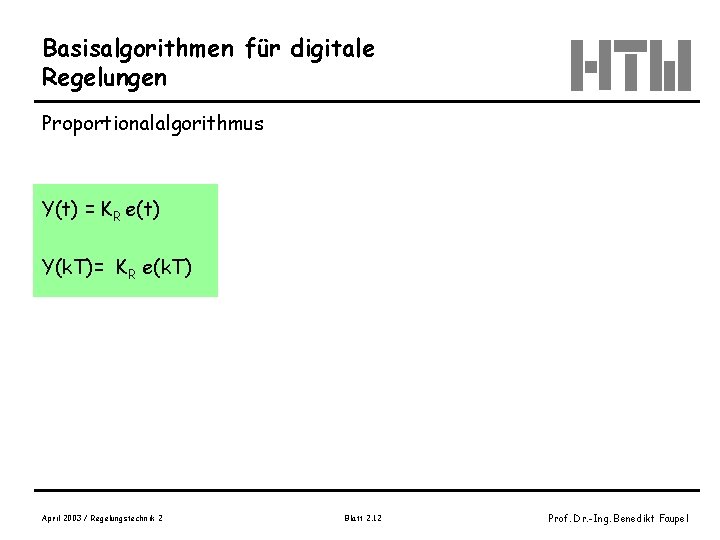
Basisalgorithmen für digitale Regelungen Proportionalalgorithmus Y(t) = KR e(t) Y(k. T)= KR e(k. T) April 2003 / Regelungstechnik 2 Blatt 2. 12 Prof. Dr. -Ing. Benedikt Faupel

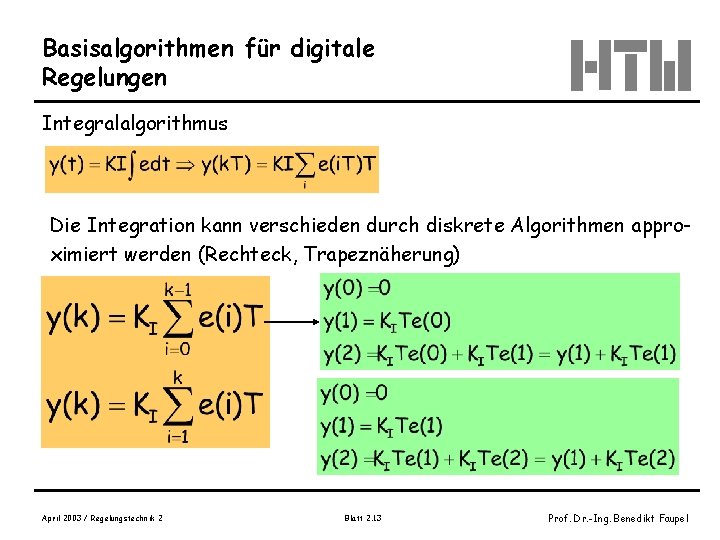
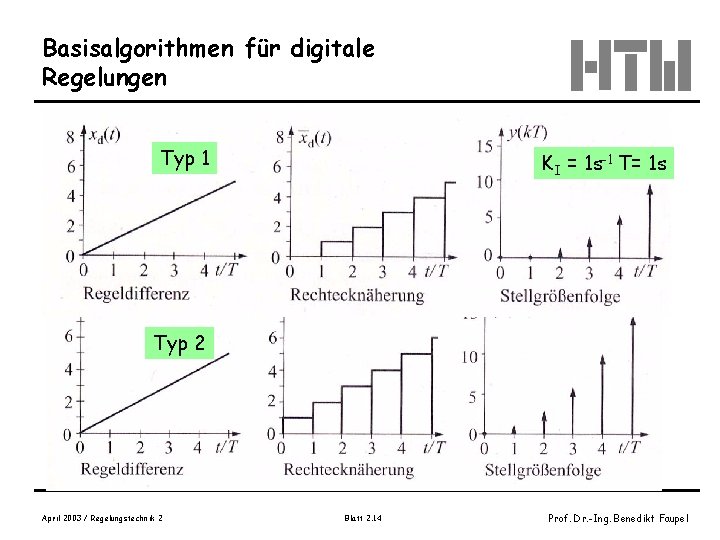
Basisalgorithmen für digitale Regelungen Integralalgorithmus Die Integration kann verschieden durch diskrete Algorithmen approximiert werden (Rechteck, Trapeznäherung) April 2003 / Regelungstechnik 2 Blatt 2. 13 Prof. Dr. -Ing. Benedikt Faupel

Basisalgorithmen für digitale Regelungen Typ 1 KI = 1 s-1 T= 1 s Typ 2 April 2003 / Regelungstechnik 2 Blatt 2. 14 Prof. Dr. -Ing. Benedikt Faupel

Basisalgorithmen für digitale Regelungen April 2003 / Regelungstechnik 2 Blatt 2. 15 Prof. Dr. -Ing. Benedikt Faupel

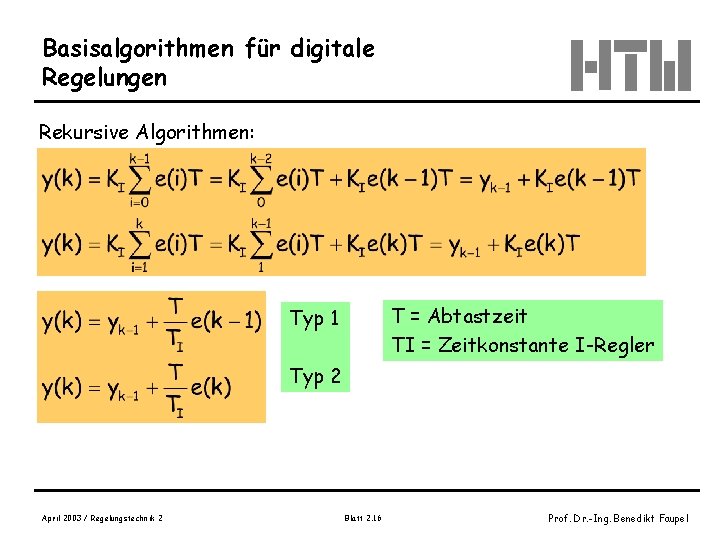
Basisalgorithmen für digitale Regelungen Rekursive Algorithmen: T = Abtastzeit TI = Zeitkonstante I-Regler Typ 1 Typ 2 April 2003 / Regelungstechnik 2 Blatt 2. 16 Prof. Dr. -Ing. Benedikt Faupel

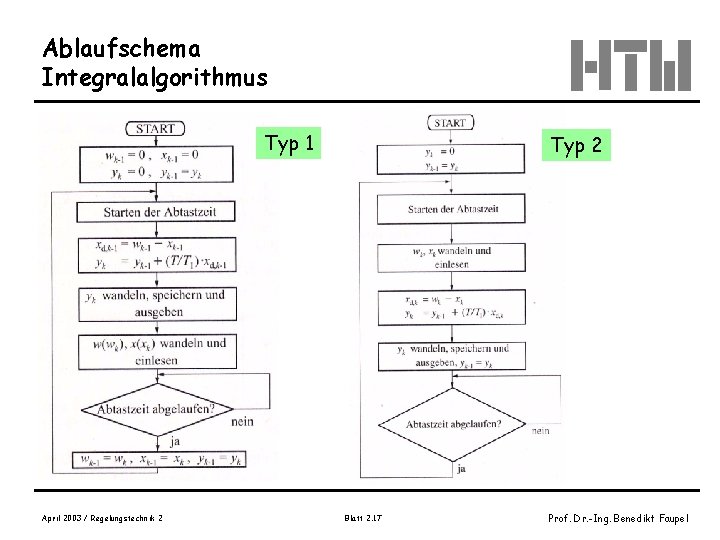
Ablaufschema Integralalgorithmus Typ 1 April 2003 / Regelungstechnik 2 Typ 2 Blatt 2. 17 Prof. Dr. -Ing. Benedikt Faupel

Beispiel mit I-Regler und PStrecke Nach der Sprungaufschaltung werden sofort alle Werte abgetastet und für die Regelung zur Verfügung gestellt: April 2003 / Regelungstechnik 2 Blatt 2. 18 Prof. Dr. -Ing. Benedikt Faupel

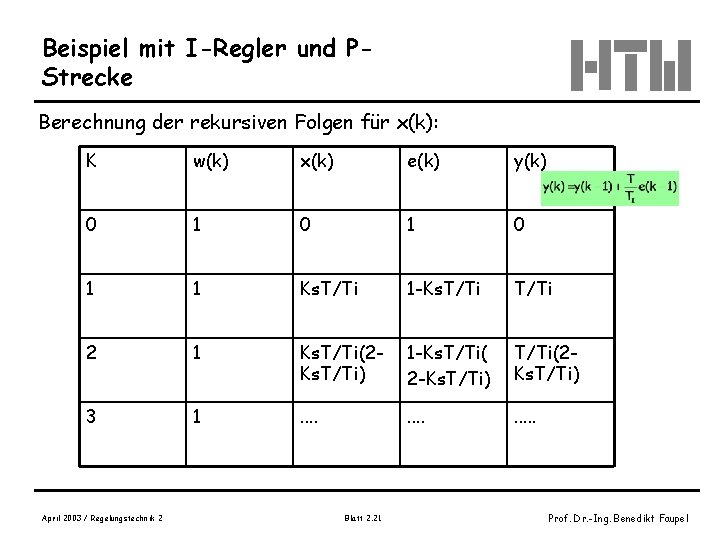
Beispiel mit I-Regler und PStrecke Berechnung der rekursiven Folgen für x(k): April 2003 / Regelungstechnik 2 Blatt 2. 19 Prof. Dr. -Ing. Benedikt Faupel

Beispiel mit I-Regler und PStrecke Berechnung der rekursiven Folgen für x(k): April 2003 / Regelungstechnik 2 Blatt 2. 20 Prof. Dr. -Ing. Benedikt Faupel

Beispiel mit I-Regler und PStrecke Berechnung der rekursiven Folgen für x(k): K w(k) x(k) e(k) y(k) 0 1 0 1 1 Ks. T/Ti 1 -Ks. T/Ti 2 1 Ks. T/Ti(2 Ks. T/Ti) 1 -Ks. T/Ti( 2 -Ks. T/Ti) T/Ti(2 Ks. T/Ti) 3 1 . . . April 2003 / Regelungstechnik 2 Blatt 2. 21 Prof. Dr. -Ing. Benedikt Faupel

Beispiel mit Zahlenwerten April 2003 / Regelungstechnik 2 K X(k) 0 0 1 0. 2 2 0. 36 3 . . . 4 . . . Blatt 2. 22 Prof. Dr. -Ing. Benedikt Faupel

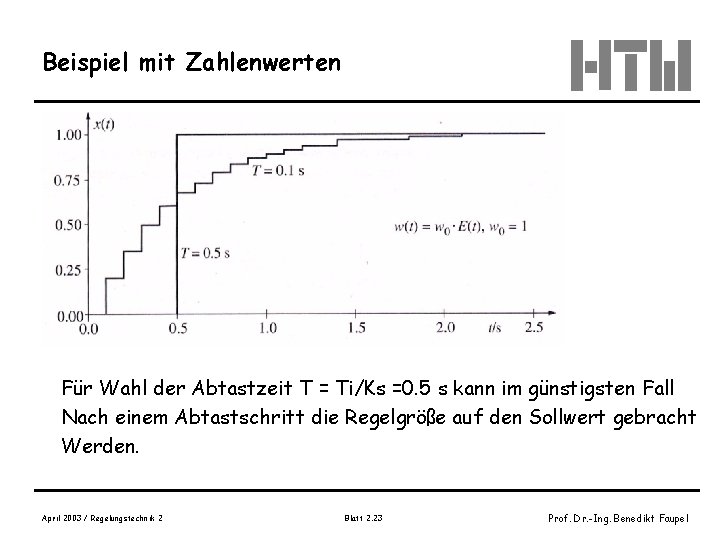
Beispiel mit Zahlenwerten Für Wahl der Abtastzeit T = Ti/Ks =0. 5 s kann im günstigsten Fall Nach einem Abtastschritt die Regelgröße auf den Sollwert gebracht Werden. April 2003 / Regelungstechnik 2 Blatt 2. 23 Prof. Dr. -Ing. Benedikt Faupel

Weitere Regelalgorithmen Nächste Stunde: • Weitere Regelalgorithmen für PI, D, PID-Regler • Rekursive Algorithmen zur Berechnung von e(k), y(k) und x(k) • Basis jeweils Regelkreis mit A/D-Wandlung, Halteelemente und D/A Wandlung • Variation neben den Regelparametern auch Einfluss der Abtastzeit Bewertung digitale Regelkreise: • Kombinierte Analyse von diskreten und analogen Elementen • Andere Beschreibungsformen nur im diskreten Bereich anwendbar April 2003 / Regelungstechnik 2 Blatt 2. 24 Prof. Dr. -Ing. Benedikt Faupel

Mathematische Grundlagen Beschreibung diskreter Signale im Zeitbereich erfolgt mathematisch mit Zahlenfolgen: • Definitionsbereich umfasst alle natürlichen Zahlen einschließlich der Null • Werte heißen Glieder Folge • Die natürlichen Zahlen des Definitionsbereiches legen die Plätze der Glieder fest. • Folge ist in der Regel nicht abbrechend • Eine Folge kann auf unterschiedliche Art und Weise beschrieben werden. April 2003 / Regelungstechnik 2 Blatt 2. 25 Prof. Dr. -Ing. Benedikt Faupel

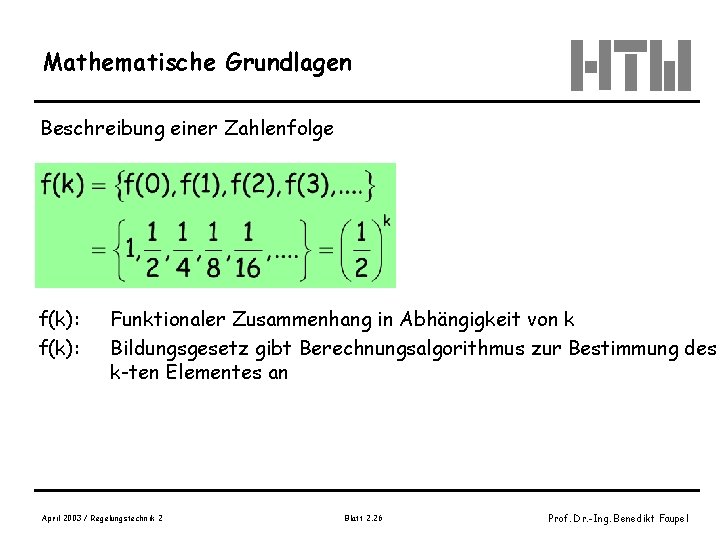
Mathematische Grundlagen Beschreibung einer Zahlenfolge f(k): Funktionaler Zusammenhang in Abhängigkeit von k Bildungsgesetz gibt Berechnungsalgorithmus zur Bestimmung des k-ten Elementes an April 2003 / Regelungstechnik 2 Blatt 2. 26 Prof. Dr. -Ing. Benedikt Faupel

Mathematische Grundlagen Beschränkte Zahlenfolge Beschränkte Folge • Die Glieder Folge überschreiten eine beliebig vorgegebene Schranke nicht. • Wächst die Folge dagegen + oder - , dann ist die Folge unbeschränkt. • Die Zu- oder Abnahme einer Folge heißt monoton, wenn jedes Glied größer bzw. kleiner als das vorangehende Glied ist. April 2003 / Regelungstechnik 2 Blatt 2. 27 Prof. Dr. -Ing. Benedikt Faupel

Mathematische Grundlagen Divergente und konvergente Zahlenfolge Folge • Diese Folge ist nicht monoton, da sich nachfolgende Glieder nicht immer größer oder kleiner als die vorangehenden Glieder sind. • Die Folge ist beschränkt, da es eine maximale Schranke gibt, unterhalb derer alle Zahlenwerte liegen. • Die Folge ist konvergent, da die Glieder Folge gegen einen bestimmten Grenzwert (für k-> ) streben. Divergente Folge April 2003 / Regelungstechnik 2 Blatt 2. 28 Prof. Dr. -Ing. Benedikt Faupel

Mathematische Grundlagen geometrische Zahlenfolge Geometrische Folge • Quotient zweier aufeinanderfolgender Glieder ist konstant. • Die k-te Teilsumme lässt sich einfach berechnen. • Für k-> geht die Folge in die geometrische Reihe über. • Ist q<1, dann konvergiert die Zahlenfolge. April 2003 / Regelungstechnik 2 Blatt 2. 29 Prof. Dr. -Ing. Benedikt Faupel

Mathematische Grundlagen geometrische Zahlenfolge April 2003 / Regelungstechnik 2 Blatt 2. 30 Prof. Dr. -Ing. Benedikt Faupel

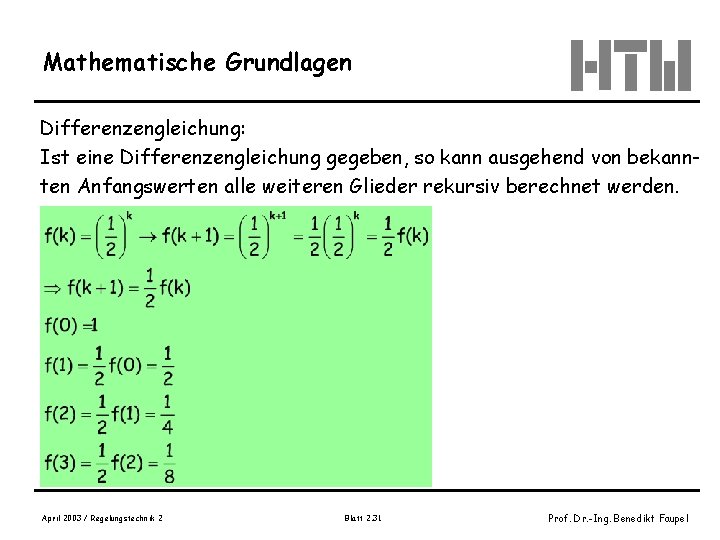
Mathematische Grundlagen Differenzengleichung: Ist eine Differenzengleichung gegeben, so kann ausgehend von bekannten Anfangswerten alle weiteren Glieder rekursiv berechnet werden. April 2003 / Regelungstechnik 2 Blatt 2. 31 Prof. Dr. -Ing. Benedikt Faupel

Mathematische Grundlagen Differenzengleichung: Differenzengleichungen entsprechen Dgl im analogen Bereich. Sind die Koeffizienten konstant, dann spricht man von LTI-Systemen Linearitätsprinzipien sind anwendbar. Lösung von Differenzengleichung im Zeitbereich Anwendung mit Exponentialansatz yh(k) = zk Homogene Lösung: setze x(k) = 0 und bestimme die Lösung für Anfangswerte Partikuläre Lösung: Ansatz mit gegebenen u(k) anschließend Bestimmung der Konstanten April 2003 / Regelungstechnik 2 Blatt 2. 32 Prof. Dr. -Ing. Benedikt Faupel

Mathematische Grundlagen Beispiel: Gesucht ist die Lösung für y(k) die folgende Differenzengleichung mit den Anfangsbedingungen erfüllt. Homogene Lösung mit Setzen von u(k)=0: April 2003 / Regelungstechnik 2 Blatt 2. 33 Prof. Dr. -Ing. Benedikt Faupel

Mathematische Grundlagen Beispiel: Partikuläre Lösung: April 2003 / Regelungstechnik 2 Blatt 2. 34 Prof. Dr. -Ing. Benedikt Faupel

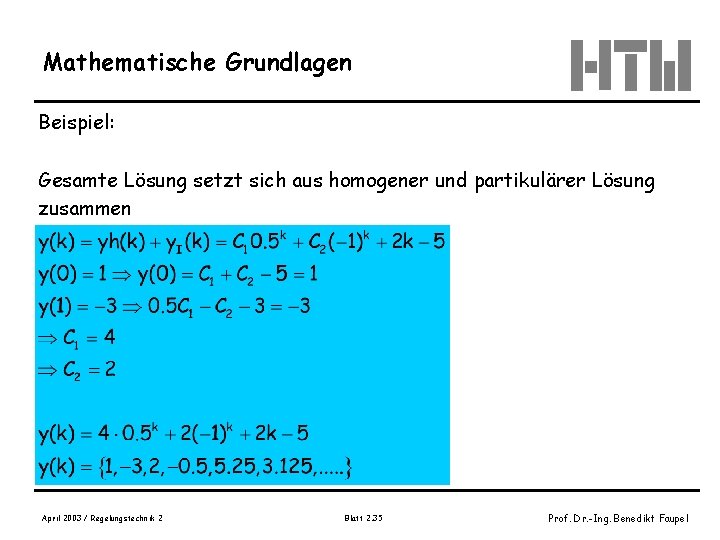
Mathematische Grundlagen Beispiel: Gesamte Lösung setzt sich aus homogener und partikulärer Lösung zusammen April 2003 / Regelungstechnik 2 Blatt 2. 35 Prof. Dr. -Ing. Benedikt Faupel

Mathematische Grundlagen Z-Transformation • anwendbar für Folgen, die erst beim Argument 0 und höher beginnen. Definition April 2003 / Regelungstechnik 2 Blatt 2. 36 Prof. Dr. -Ing. Benedikt Faupel

Mathematische Grundlagen Z-Transformation f(k) <-> F(z) Beispiel Exponentialfolge: Anwendung der geometrischen Reihe Konvergenzkriterium muss erfüllt werden: |a/z|<1 ->|a|<|z| April 2003 / Regelungstechnik 2 Blatt 2. 37 Prof. Dr. -Ing. Benedikt Faupel

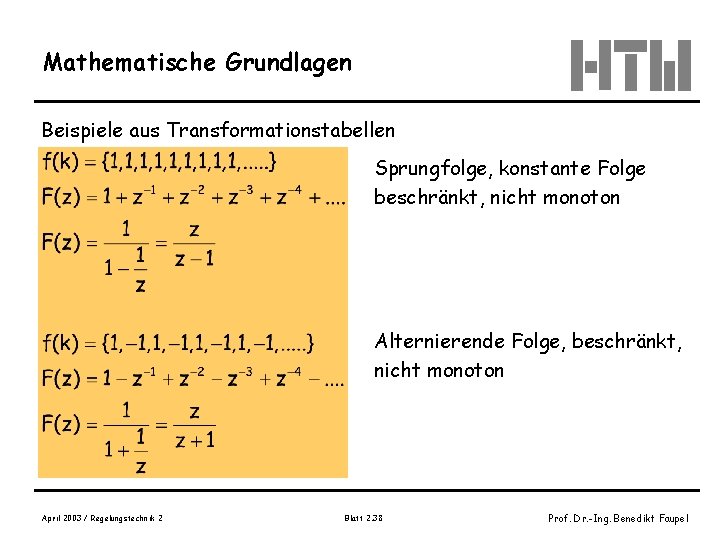
Mathematische Grundlagen Beispiele aus Transformationstabellen Sprungfolge, konstante Folge beschränkt, nicht monoton Alternierende Folge, beschränkt, nicht monoton April 2003 / Regelungstechnik 2 Blatt 2. 38 Prof. Dr. -Ing. Benedikt Faupel

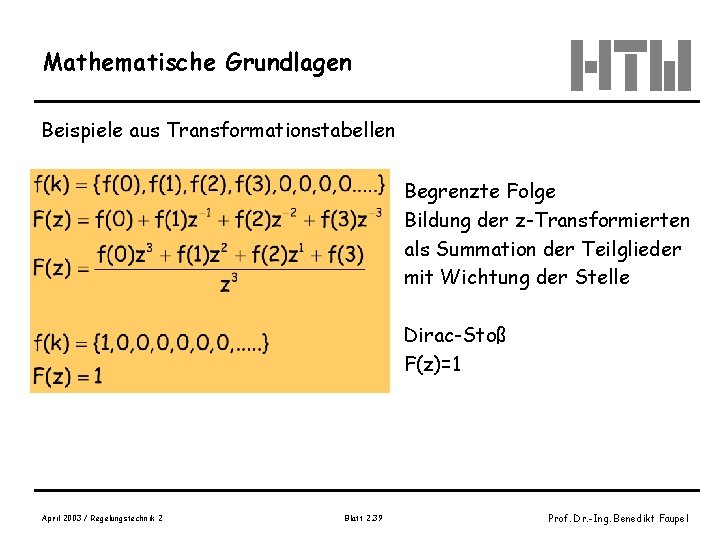
Mathematische Grundlagen Beispiele aus Transformationstabellen Begrenzte Folge Bildung der z-Transformierten als Summation der Teilglieder mit Wichtung der Stelle Dirac-Stoß F(z)=1 April 2003 / Regelungstechnik 2 Blatt 2. 39 Prof. Dr. -Ing. Benedikt Faupel

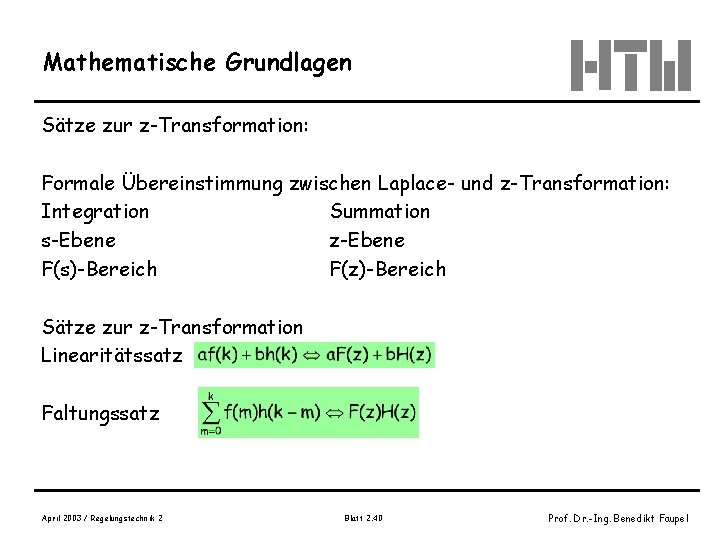
Mathematische Grundlagen Sätze zur z-Transformation: Formale Übereinstimmung zwischen Laplace- und z-Transformation: Integration Summation s-Ebene z-Ebene F(s)-Bereich F(z)-Bereich Sätze zur z-Transformation Linearitätssatz Faltungssatz April 2003 / Regelungstechnik 2 Blatt 2. 40 Prof. Dr. -Ing. Benedikt Faupel

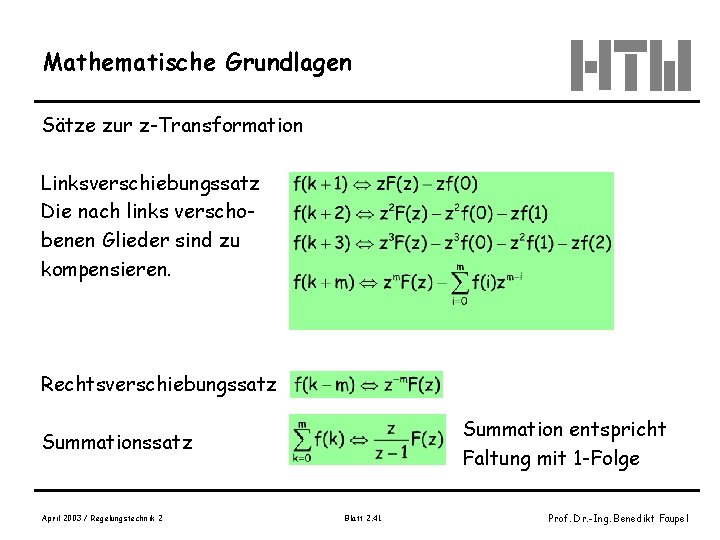
Mathematische Grundlagen Sätze zur z-Transformation Linksverschiebungssatz Die nach links verschobenen Glieder sind zu kompensieren. Rechtsverschiebungssatz Summation entspricht Faltung mit 1 -Folge Summationssatz April 2003 / Regelungstechnik 2 Blatt 2. 41 Prof. Dr. -Ing. Benedikt Faupel

Mathematische Grundlagen Sätze zur z-Transformation Beispiel zum Linksverschiebungssatz: April 2003 / Regelungstechnik 2 Blatt 2. 42 Prof. Dr. -Ing. Benedikt Faupel

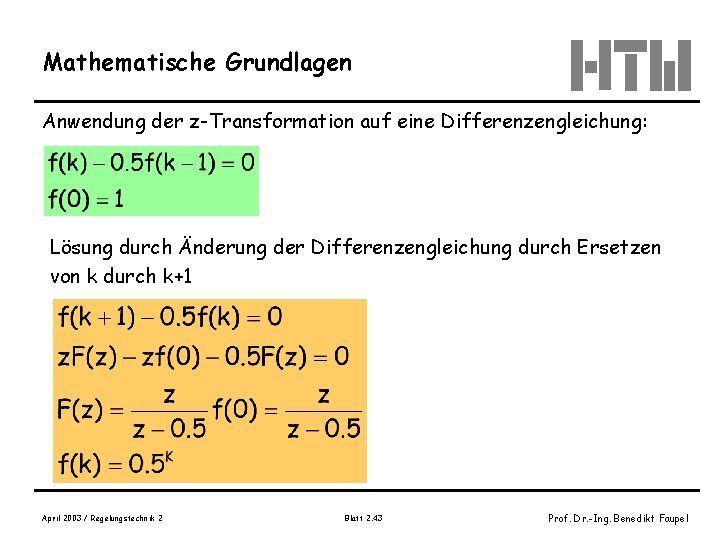
Mathematische Grundlagen Anwendung der z-Transformation auf eine Differenzengleichung: Lösung durch Änderung der Differenzengleichung durch Ersetzen von k durch k+1 April 2003 / Regelungstechnik 2 Blatt 2. 43 Prof. Dr. -Ing. Benedikt Faupel

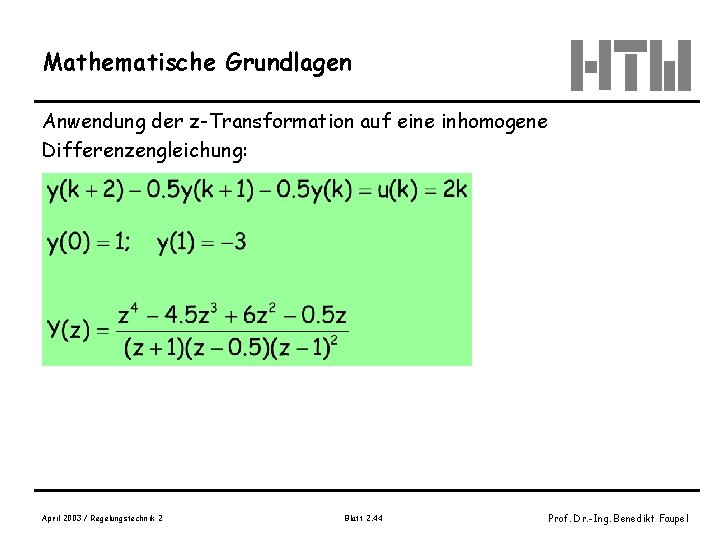
Mathematische Grundlagen Anwendung der z-Transformation auf eine inhomogene Differenzengleichung: April 2003 / Regelungstechnik 2 Blatt 2. 44 Prof. Dr. -Ing. Benedikt Faupel

Mathematische Grundlagen Anwendung der z-Transformation auf eine inhomogene Differenzengleichung: April 2003 / Regelungstechnik 2 Blatt 2. 45 Prof. Dr. -Ing. Benedikt Faupel

Mathematische Grundlagen Anwendung der z-Transformation auf eine inhomogene Differenzengleichung: April 2003 / Regelungstechnik 2 Blatt 2. 46 Prof. Dr. -Ing. Benedikt Faupel

Literatur Regelungstechnik Literaturliste: • Lutz, H. ; Wendt, W. : Taschenbuch der Regelungstechnik, Verlag Harri Deutsch, Frankfurt, 1998 ISBN 3 -8171 -1552 -0 (Bibliothek HTW) • Unbehauen, H. : Regelungstechnik II, Vieweg-Verlag, Braunschweig, 2001, ISBN 3 -528 -01332 -X • Schlüter Gerd. : Digitale Regelungstechnik interaktiv, Fachbuchverlag Leipzig, 2000, ISBN 3 -446 -21477 -1 • Merz, Jaschek: Regelungstechnik, Vorlesung Universität Saarbrücken • Gassmann, Hugo: Theorie der Regelungstechnik. Eine Einführung, Verlag Harri Deutsch, Frankfurt, 1998. ISBN-3 -8171 -1587 -3 (Bibliothek HTW) April 2003 / Regelungstechnik 2 Blatt 2. 47 Prof. Dr. -Ing. Benedikt Faupel