Vorlesung Finanzmathematik und Risikomanagement Jrg Lemm WS 20078

Vorlesung Finanzmathematik und Risikomanagement Jörg Lemm WS 2007/8

Basel, die Banken und die Physiker Basler Ausschuss der G 10 Länder zur Bankenaufsicht erarbeitet Richtlinien zur Eigenkapitalunterlegung von Bankrisiken 1988 Basel I, Vorschriften zur (pauschalen) Eigenkapitalunterlegung von Kreditrisiken 1996 Erweiterung auf Marktrisiko (Physiker als Entwickler interner Marktrisikomodelle) 1999 Basel II, erstes Konsultationspapier Kreditrisiko (Physiker als Entwickler von Methoden der Kreditrisikomessung – und steuerung) 2007 Inkrafttreten Solvabilitätsverordnung (Basel II)

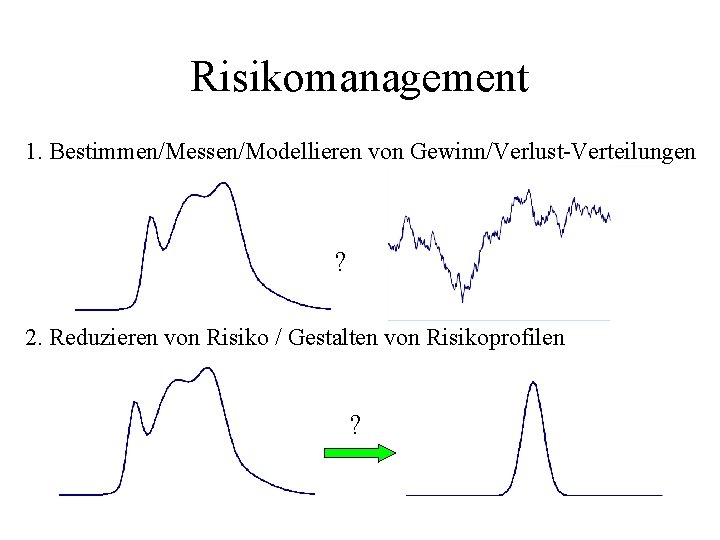
Risikomanagement 1. Bestimmen/Messen/Modellieren von Gewinn/Verlust-Verteilungen ? 2. Reduzieren von Risiko / Gestalten von Risikoprofilen ?

Marktrisiko • Einzelkurse: Probabilistische Modelle • Portfolio: Risikominimierung • Hedging: Geht es ohne Risiko?

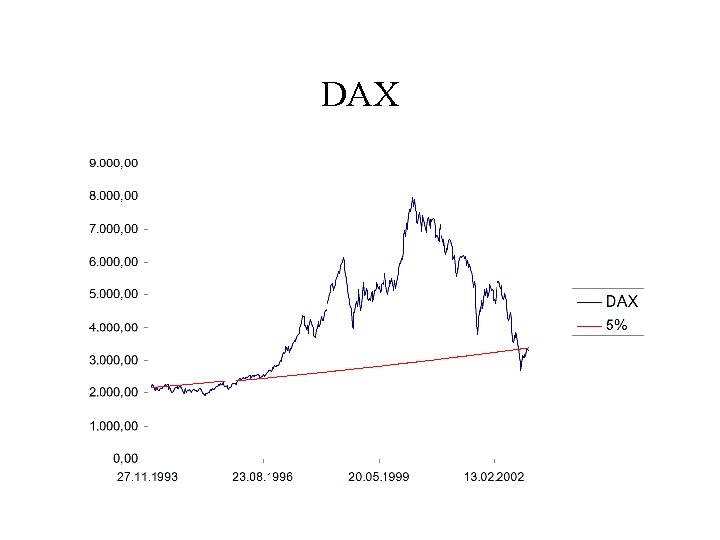
DAX

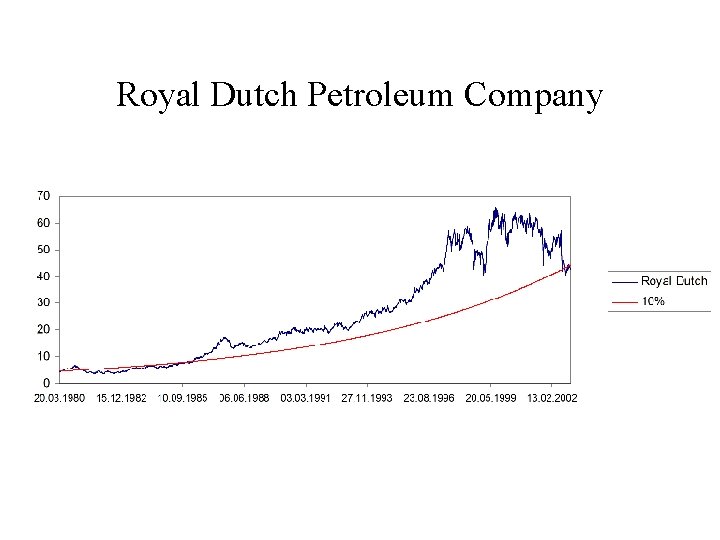
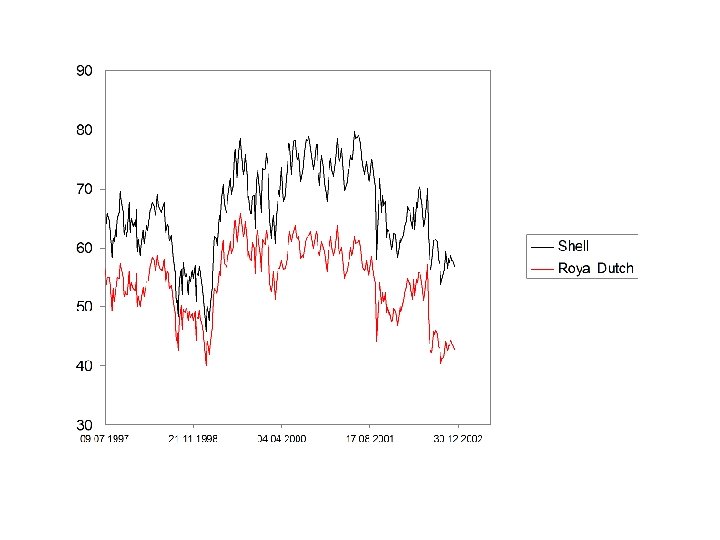
Royal Dutch Petroleum Company

Brown´sche Bewegung Unabhängige, normalverteilte Zuwächse mit (bei kleinen Zeiten) Mittelwert 0 also (Bachelier 1900, Einstein 1905) Markteffizienz (Fama 1970, U. of Chicago) Beispiel Brown‘sche Bewegung mit Varianz

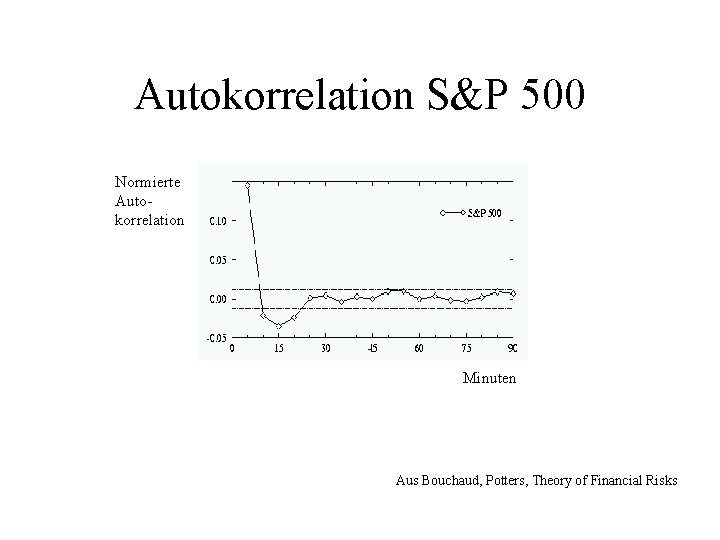
Autokorrelation S&P 500 Normierte Autokorrelation Minuten Aus Bouchaud, Potters, Theory of Financial Risks

Geometrische Brown´sche Bewegung ist eine Brown´sche Bewegung bezogen auf logarithmische Preise, mit normalverteilten Renditen (relative Preisänderungen) mit also Beispiel geometrische Brown‘sche Bewegung

ARCH-Prozesse A(uto)R(egressive) C(onditional) H(eteroscedasticity) Wie eine (geometrische) Brown´sche Bewegung, aber mit einer veränderlichen Varianz, abhängig von (einem `moving average´ der) vergangenen quadrierten Änderungen. ARCH(p) : Beispiel ARCH-Prozess

GARCH-Prozesse G(eneralized) A(uto)R(egressive) C(onditional) H(eteroscedasticity) Wie eine (geometrische) Brown´sche Bewegung, aber mit einer veränderlichen Varianz, abhängig von (einem `moving average´ der) vergangenen quadrierten Änderungen sowie der vergangenen Varianz selbst (`autoregressive Komponente´) GARCH(1, 1) : Beispiel GARCH-Prozess

Kursvorhersage: Probleme • Schwankungen sind besser vorhersagbar als Renditen • Langfristige systematische Vorhersagemöglichkeiten erlauben Arbitrage (risikolose Gewinne) und sind daher in größerem Umfang nicht zu erwarten • Es gibt keine notwendige kurzfristige Kopplung an den Fundamentalwert. Positive Rückkopplungen führen zu Spekulationsblasen (Bsp. : Stop loss orders, Behavioral Finance, Kahnemann & Tversky) • Nutzen von Expertenwissen ( Bayes‘sche Methoden) empirisch schwer überprüfbar

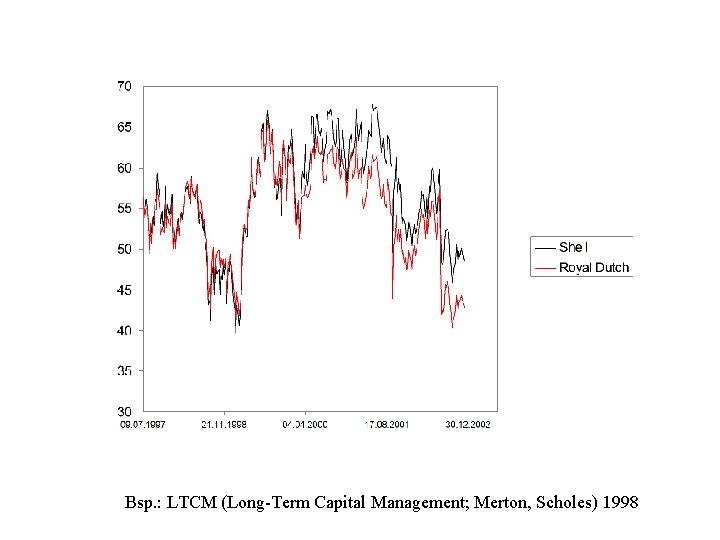
Bsp. : LTCM (Long-Term Capital Management; Merton, Scholes) 1998

Marktrisiko • Einzelkurse: Probabilistische Modelle • Portfolio: Risikominimierung • Hedging: Geht es ohne Risiko?

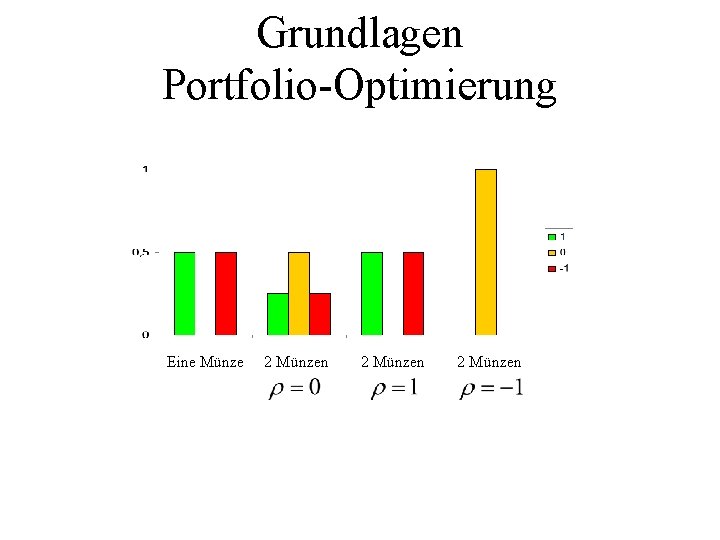
Grundlagen Portfolio-Optimierung Eine Münze 2 Münzen

Problemstellung Portfolio-Optimierung Portfoliozusammensetzung: (relativer) Anteil von Aktie 1 (relativer) Anteil von Aktie 2 (relativer) Anteil von Aktie 3. . . Problemstellung: Finde für vorgegebene Gewinnerwartung die Portfoliozusammensetzung mit minimalem Risiko (Varianz) (Physiker als Fonds- bzw. Portfoliomanager)

Markowitz 1952, Nobelpreis 1990 Portfolio-Optimierung Ein Portfolio aus Aktien mit erwartetem Gewinn Varianz-Kovarianzmatrix , und (relativen) Anteil hat die Portfoliovarianz Bei fixiertem Gesamterwartungswert (und fixierten auf 1 normierten Einstandspreis) soll die Unsicherheit (hier: Varianz) minimiert werden unter den Nebenbedingungen Korrelierte Wertpapiere und Portfolio-Optimierung

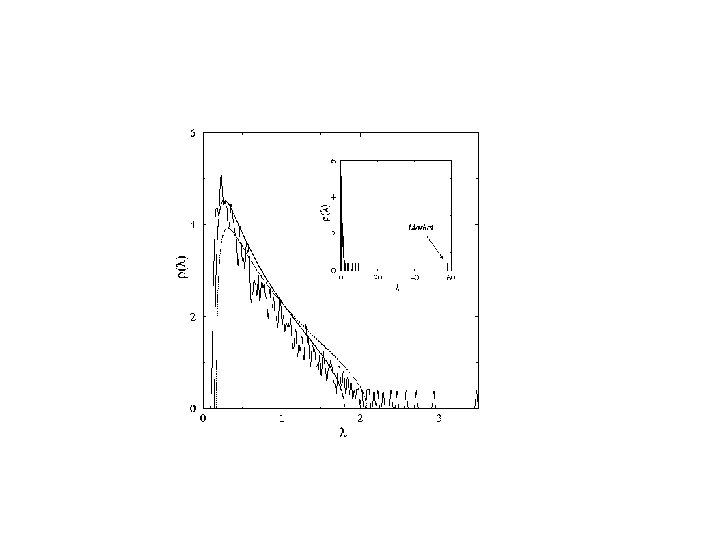
Portfolio-Optimierung: Probleme • Die Zahl der Einträge in einer Korrelationsmatrix wächst quadratisch mit der Zahl der Komponenten • historische Daten zeigen starkes Rauschen (Filtern mit Random Matrix Methoden) • historische Werte sind nur von bedingtem Nutzen A-Priori Informationen müssen mit einfließen (Bayes‘sche Methoden) • Andere Risikomaße (z. B. Va. R) und Nicht-Gauß‘sche Verteilungen (Monte Carlo) • Viele verschiedene Nebenbedingungen möglich (teilweise Zusammenhang mit Spingläsern, dann viele Minima) • Optimale Portfolios sind nicht sehr stabil • Transaktionskosten und fehlende Liquidität

Marktrisiko • Einzelkurse: Probabilistische Modelle • Portfolio: Risikominimierung • Hedging: Geht es ohne Risiko?

Optionspreisformeln, Black, Scholes, Merton 1973, Merton u. Scholes Nobelpreis 1997 „No-Arbitrage“-Prinzip Perfekt negativ korrelierte Finanzprodukte erlauben die Konstruktion risikoloser Portfolios Beispiel: Komplexe Finanzinstrumente (wie z. B. Optionen) können manchmal durch eine Mischung von (der Option zugrundeliegenden) Aktien und einer risikolosen Geldanlage nachgebildet werden: Option = a*Aktie + b*Geldkonto (Physiker als Finanzingenieure) Binomialmodell Aktie Binomialmodell 1 stufig Binomialmodell Derivate Binomialmodell 2 stufig

No-Arbitrage Prinzip: Probleme • Kontinuierliches Handeln ohne Transaktionskosten • Restriktive Verteilungsannahmen (log-normale Kurse mit bekannter Zinsrate und Volatilität) • Leerverkäufe erlaubt, Aktien beliebig teilbar • Erweiterungen (z. B. Monte Carlo) sind oft aufwendig und führen nicht immer zu kompletter Risikofreiheit

Kreditrisiko • Einzelkredit: Erwarteter Verlust • Portfolio: Unerwarteter Verlust • Pricing: Was kostet Risiko?

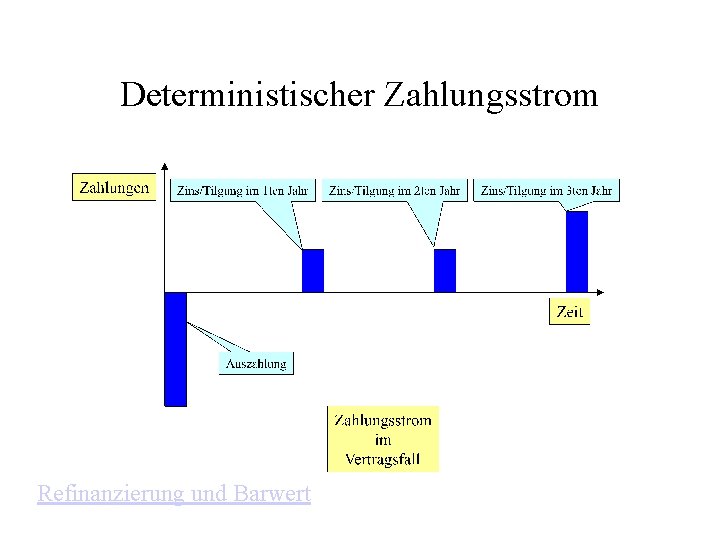
Deterministischer Zahlungsstrom Refinanzierung und Barwert

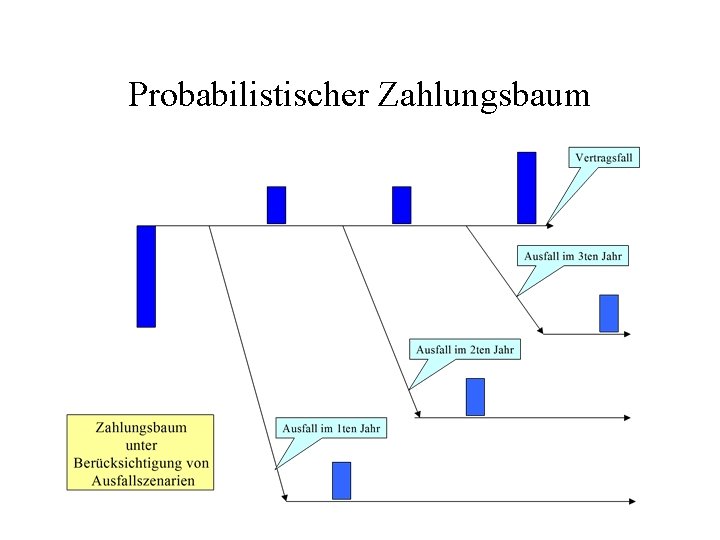
Probabilistischer Zahlungsbaum

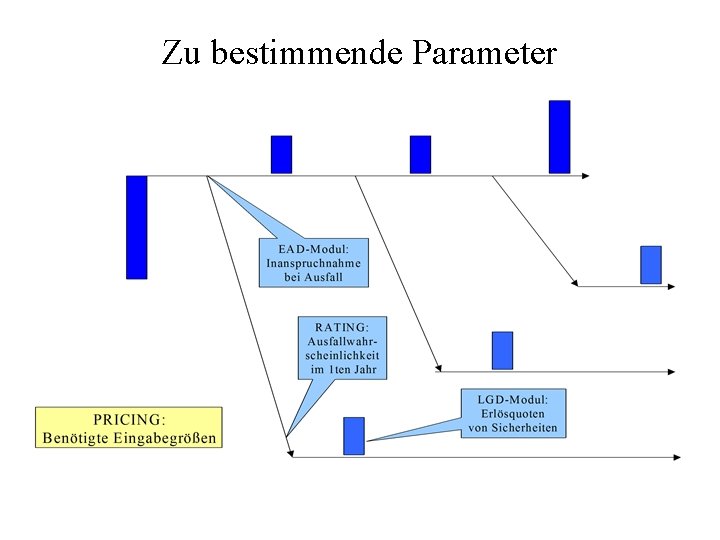
Zu bestimmende Parameter

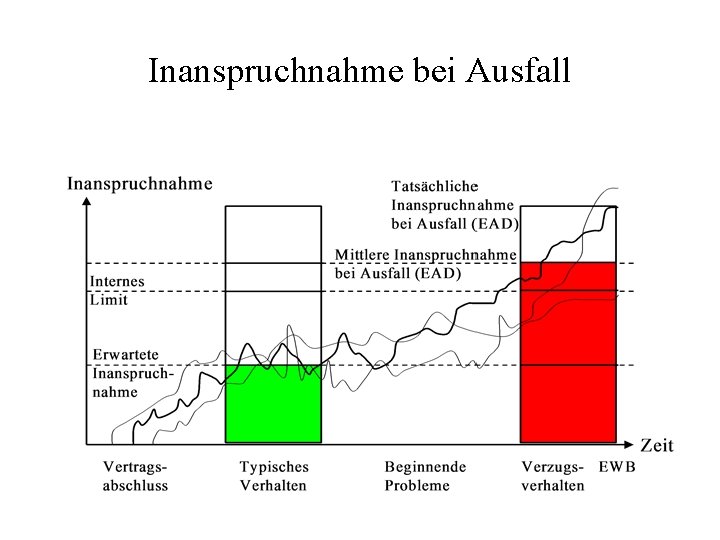
Inanspruchnahme bei Ausfall

Ausfallwahrscheinlichkeiten durch logistische Regression Die Ausfallwahrscheinlichkeit für gegebenen Scorewert x lässt sich analog schreiben als Für die „Energiedifferenz“ lassen sich nun verschiedene Ansätze wählen. Ein einfacher linearer Ansatz führt zur logistischen Regression Logistische Regression RBF

Maximum Likelihood Methode Es werden diejenigen Modellparameter a und b ausgewählt unter denen die Wahrscheinlichkeit der gegebenen Daten p(Daten|Modell) ( = „Likelihood“) maximal wird. Für gegebenen Scorewert x ist die Likelihood für die Ausfallvariable y Für nichtparametrische Verfahren (mit vielen Freiheitsgraden) muss die Maximum Likelihood Methode durch Cross-Validierungstechniken oder Hinzunahme von A-Priori-Informationen (Bayes‘sche Statistik) ergänzt werden. Logistische Regression RBF

Kreditrisiko • Einzelkredit: Erwarteter Verlust • Portfolio: Unerwarteter Verlust • Pricing: Was kostet Risiko?

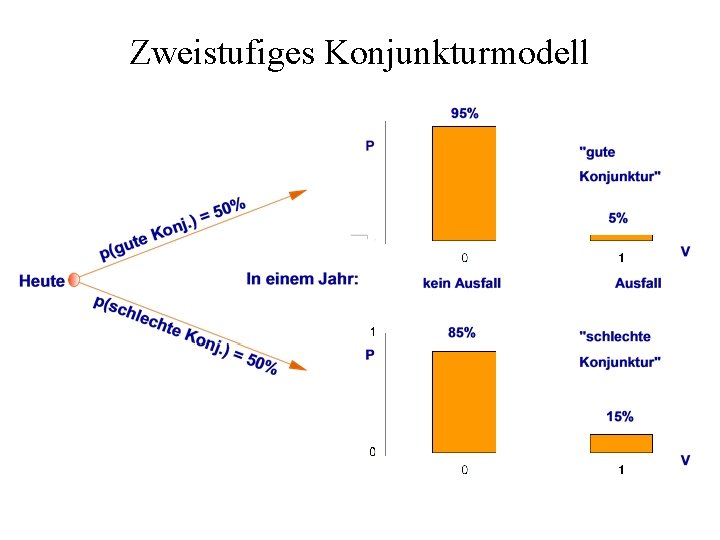
Zweistufiges Konjunkturmodell

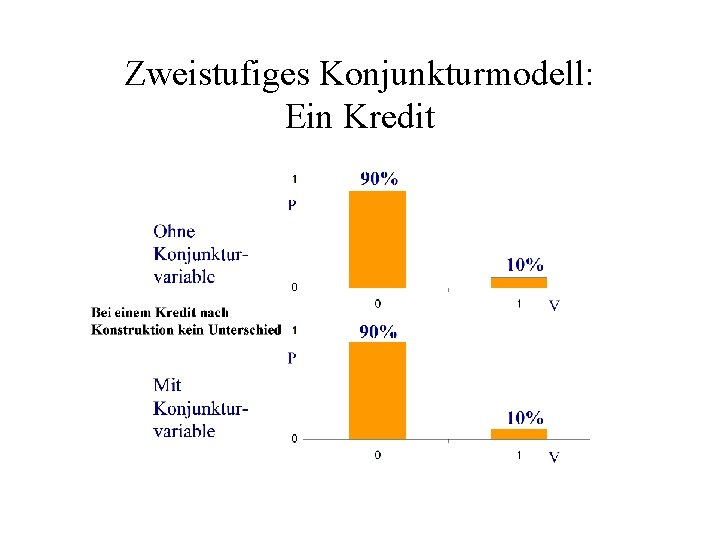
Zweistufiges Konjunkturmodell: Ein Kredit

Zweistufiges Konjunkturmodell: 2 Kredite P 81% Unabhängige Kredite 18% 1% kein Ausfall P 81, 25% Abhängige Kredite ein Ausfall Größere Häufigkeit eines Doppelausfalls bei abhängigen Krediten 17, 5% kein Ausfall Doppelausfall ein Ausfall 1, 25% Doppelausfall

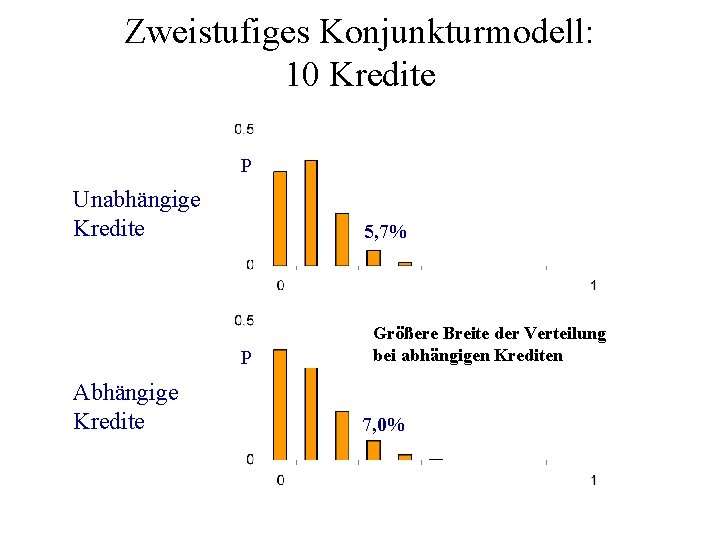
Zweistufiges Konjunkturmodell: 10 Kredite P Unabhängige Kredite 5, 7% P Abhängige Kredite Größere Breite der Verteilung bei abhängigen Krediten 7, 0%

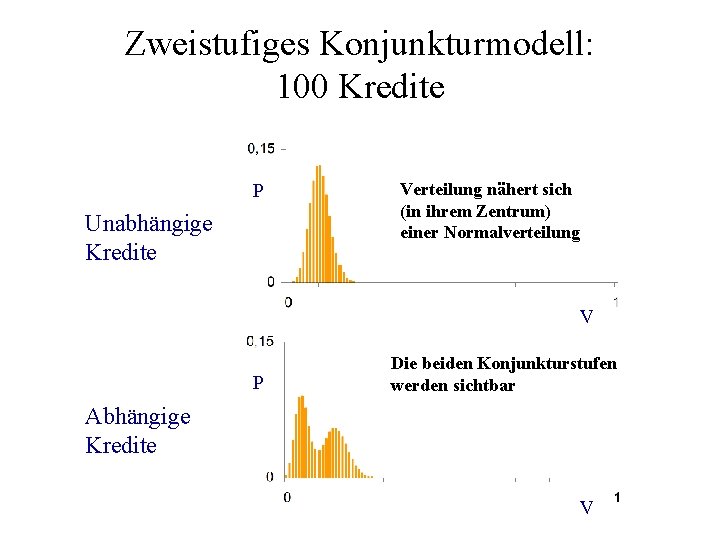
Zweistufiges Konjunkturmodell: 100 Kredite P Unabhängige Kredite Verteilung nähert sich (in ihrem Zentrum) einer Normalverteilung V P Die beiden Konjunkturstufen werden sichtbar Abhängige Kredite V

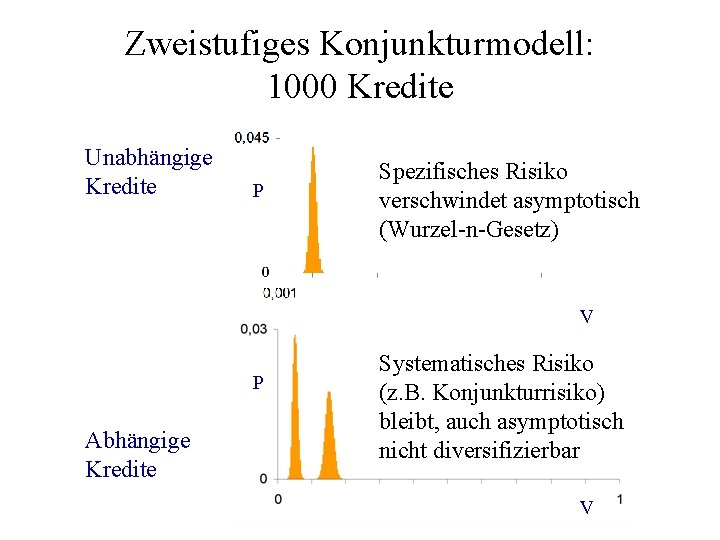
Zweistufiges Konjunkturmodell: 1000 Kredite Unabhängige Kredite P Spezifisches Risiko verschwindet asymptotisch (Wurzel-n-Gesetz) V P Abhängige Kredite Systematisches Risiko (z. B. Konjunkturrisiko) bleibt, auch asymptotisch nicht diversifizierbar V

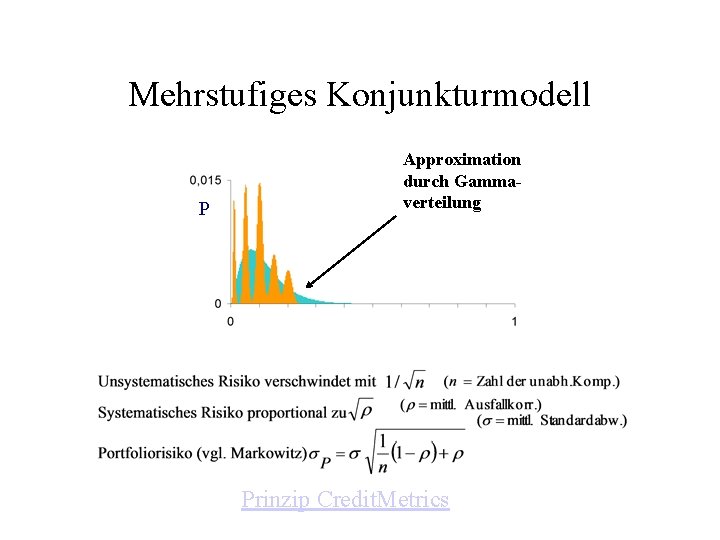
Mehrstufiges Konjunkturmodell P Approximation durch Gammaverteilung Prinzip Credit. Metrics

Restrisiko In der Praxis verschwindet das Risiko auch für sehr große Banken nicht, da 1 Zahl der Kredite noch nicht groß genug 2 Kreditvolumina sehr unterschiedlich groß (dominierende Einzelkredite, „Klumpenrisiken“ ) 3 Einzelkredite korreliert (systematisches Risiko) Aufsichtliche Unterlegungspflicht mit Eigenkapital

Kreditrisiko • Einzelkredit: Erwarteter Verlust • Portfolio: Unerwarteter Verlust • Pricing: Was kostet Risiko?

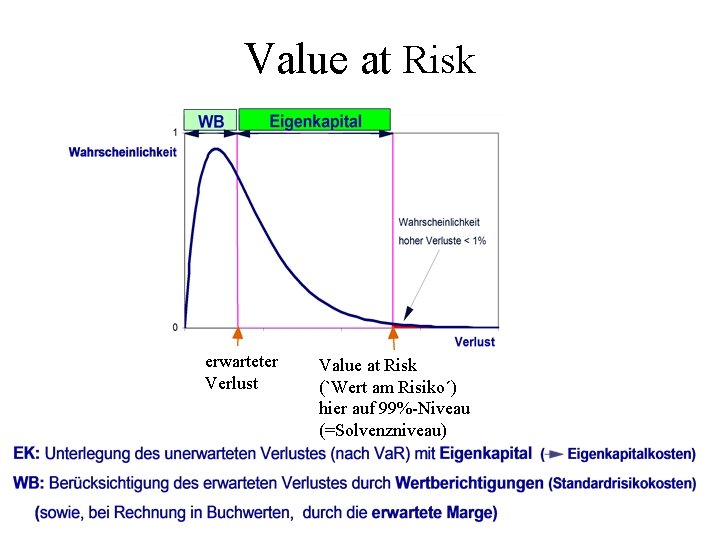
Value at Risk erwarteter Verlust Value at Risk (`Wert am Risiko´) hier auf 99%-Niveau (=Solvenzniveau)

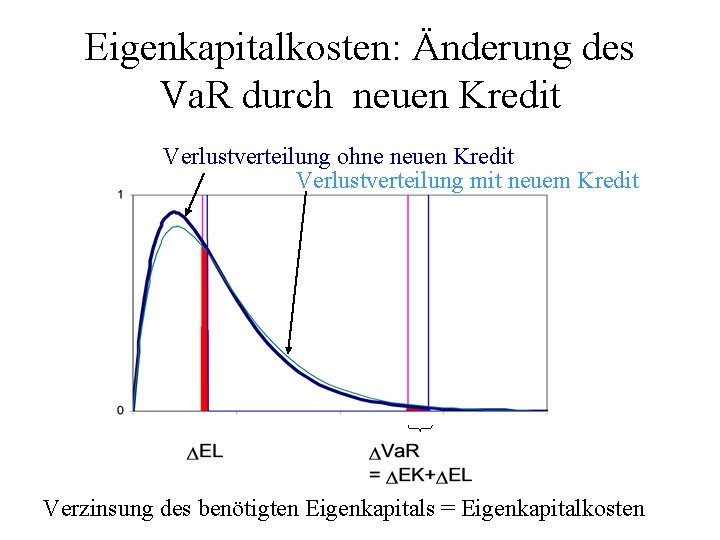
Eigenkapitalkosten: Änderung des Va. R durch neuen Kredit Verlustverteilung ohne neuen Kredit Verlustverteilung mit neuem Kredit Verzinsung des benötigten Eigenkapitals = Eigenkapitalkosten

Pricing Barwert(Vertragsfall) - erwarteter Verlust - Eigenkapitalkosten (Risikoprämie) = Nettoerfolg Pricing. Toy

Vielen Dank !

Wahrscheinlichkeit und Energie Jede Wahrscheinlichkeit(sdichte) läßt sich schreiben als mit „Energie“ und „Zustandssumme“ Vorteile: 1. Normierung und Nichtnegativität automatisch gewährleistet 2. Normierung braucht nicht in jedem Fall berechnet zu werden 3. Multiplikation von Wahrscheinlichkeiten entspricht Addition von Energien(Integrale)

Andere mögliche Nebenbedingungen Keine Leerverkäufe : Mit Marginkonto : Mit Diversifikationsvorgabe : ( Spingläser)