Vorlesung Regelungstechnik 1 Symmetrisches Optimum im Frequenzbereich 14

Vorlesung Regelungstechnik 1 Symmetrisches Optimum im Frequenzbereich 14. Januar 2003 Hochschule für Technik und Wirtschaft des Saarlandes Fachbereich Elektrotechnik Goebenstr. 40 66117 Saarbrücken Januar 2003 / Regelungstechnik Blatt 9. 1 Prof. Dr. -Ing. Benedikt Faupel

Einstellungsvarianten für Reglerparameter im Zeitbereich Optimierung Regelfläche Ziegler& Nichols Chien, Hrones, Reswick T-Summen. Regel (Kuhn) Januar 2003 / Regelungstechnik PT 2 -Strecke (PTn-Strecken) Reglerparameter optimales D od. MP PTn-Strecke Tu, Tg, K Reglerparameter P, PID GS(s) oder physikalisch Reglerparameter P, PID Bestimmung Kpkrit, Tkrit PTn-Strecke Tu, Tg, K (w) Reglerparameter P, PID MP ~ 0 MP ~ 20% PTn-Strecke Tu, Tg, K (z) Reglerparameter P, PID MP ~ 0 MP ~ 20% PTn-Strecke T Reglerparameter nur PI, PID schnelle Regelung Blatt 9. 2 Prof. Dr. -Ing. Benedikt Faupel

Einstellungsvarianten für Regelparameter im Frequenzbereich Betragsoptimum PTn-Strecken Reglerparameter I-Regler Feste Reglereinstellung PI-Regler Kompensation T 1 PID-Regler Kompensation T 1 T 2 Symmetri. optimum Frequenzkennlinienverfahren Januar 2003 / Regelungstechnik PTn-Strecken Reglerparameter PI/PID PTn-Strecken mit I-Anteil Regelparameter PI/PID Regelstrecke beliebig Blatt 9. 3 Reglerparameter P/PI/PID variable Reglereinstellung Variable Vorgaben Prof. Dr. -Ing. Benedikt Faupel

Symmetrisches Optimum Anwendung des Betragsoptimum für Regelstrecken mit I-Anteil Januar 2003 / Regelungstechnik Blatt 9. 4 Prof. Dr. -Ing. Benedikt Faupel

Symmetrisches Optimum Anwendung des Betragsoptimum für Regelstrecken mit I-Anteil: Mit Kompensation TN=TE ergibt sich folgendes Go(s): Januar 2003 / Regelungstechnik Blatt 9. 5 Prof. Dr. -Ing. Benedikt Faupel

Symmetrisches Optimum Interpretation für Anwendung des Betragsoptimum: • Phasengang bei – 180° • Grenzstabil / Instabil • Keine ideale Lösung • GW(s) hat charakteristische Gleichung: Januar 2003 / Regelungstechnik Blatt 9. 6 Prof. Dr. -Ing. Benedikt Faupel

Lösung mit symmetrischen Optimum Lösungsansatz mit Parameter a: • a > 1 liefert Phasenanhebung und führt daher zu stabilerem Verhalten. • a = 1 liefert Ansatz nach Betragsoptimum mit grenzstabilen Verhalten. • a < 1 liefert Phasenanteile von Go(s), die kleiner als – 180° sind. Führt zu instabilem Verhalten Betrachtung im Bodediagramm und Pol-Nullstellenverteilung von Go(s) Januar 2003 / Regelungstechnik Blatt 9. 7 Prof. Dr. -Ing. Benedikt Faupel

Lösung mit symmetrischen Optimum Beim symmetrischen Optimum wird der Regler so gewählt, dass eine maximale Phasenanhebung bei einer gewünschten Durchtrittsfrequenz auftritt. Der offene Regelkreis wirkt phasenanhebend bei der Wahl von a 2 > 1. Die gewünschte Durchtrittsfrequenz liegt beim geometrischen Mittel von TE und TN. Das symmetrische Optimum liefert Einstellungsregeln, wie PI und PID-Regler dimensioniert werden. Januar 2003 / Regelungstechnik Blatt 9. 8 Prof. Dr. -Ing. Benedikt Faupel

Lösung mit symmetrischen Optimum Lösungsansatz mit Januar 2003 / Regelungstechnik Blatt 9. 9 Prof. Dr. -Ing. Benedikt Faupel

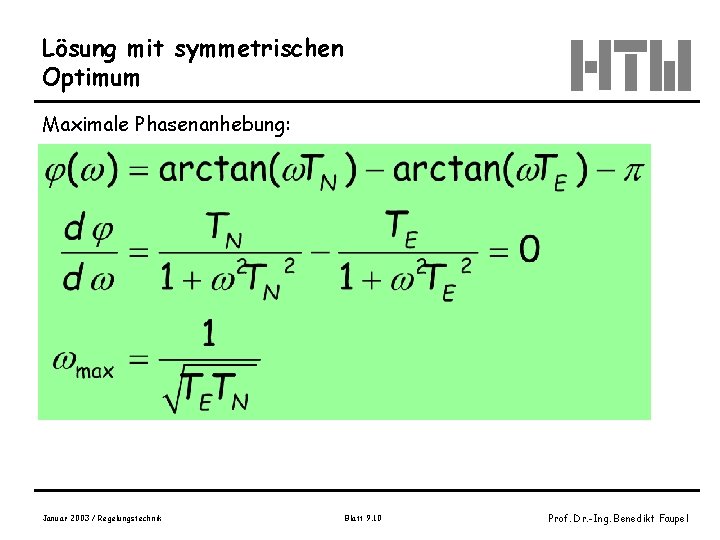
Lösung mit symmetrischen Optimum Maximale Phasenanhebung: Januar 2003 / Regelungstechnik Blatt 9. 10 Prof. Dr. -Ing. Benedikt Faupel

Lösung mit symmetrischen Optimum Gesamtamplitude von Go(s) bei maximaler Phasenanhebung: Mit TN = a 2 TE und max ergibt sich: Januar 2003 / Regelungstechnik Blatt 9. 11 Prof. Dr. -Ing. Benedikt Faupel

Lösung mit symmetrischen Optimum Kenngrößen für Reglerauslegung Januar 2003 / Regelungstechnik Blatt 9. 12 Prof. Dr. -Ing. Benedikt Faupel

Einstellung nach dem symmetrischen Optimum Mit den Optimierungsgleichungen ergibt sich: Einsetzen in G 0(s): Januar 2003 / Regelungstechnik Blatt 9. 13 Prof. Dr. -Ing. Benedikt Faupel

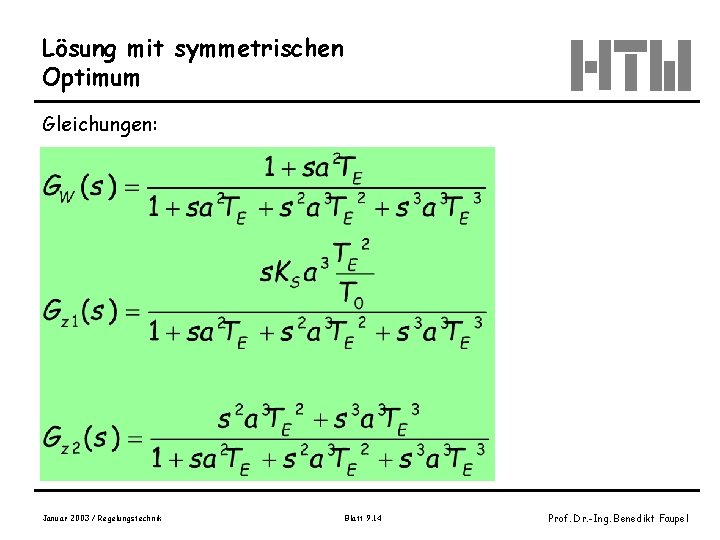
Lösung mit symmetrischen Optimum Gleichungen: Januar 2003 / Regelungstechnik Blatt 9. 14 Prof. Dr. -Ing. Benedikt Faupel

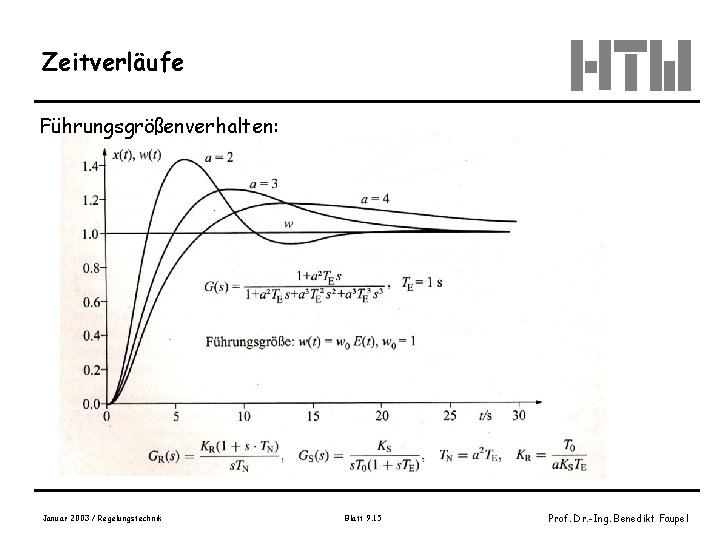
Zeitverläufe Führungsgrößenverhalten: Januar 2003 / Regelungstechnik Blatt 9. 15 Prof. Dr. -Ing. Benedikt Faupel

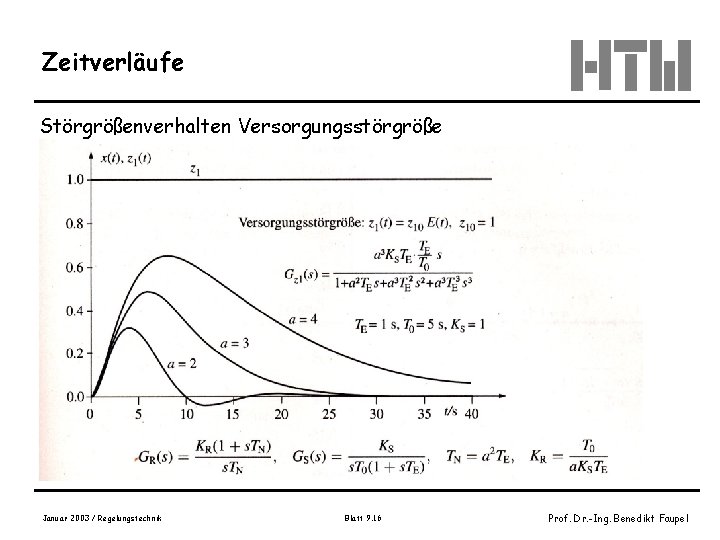
Zeitverläufe Störgrößenverhalten Versorgungsstörgröße Januar 2003 / Regelungstechnik Blatt 9. 16 Prof. Dr. -Ing. Benedikt Faupel

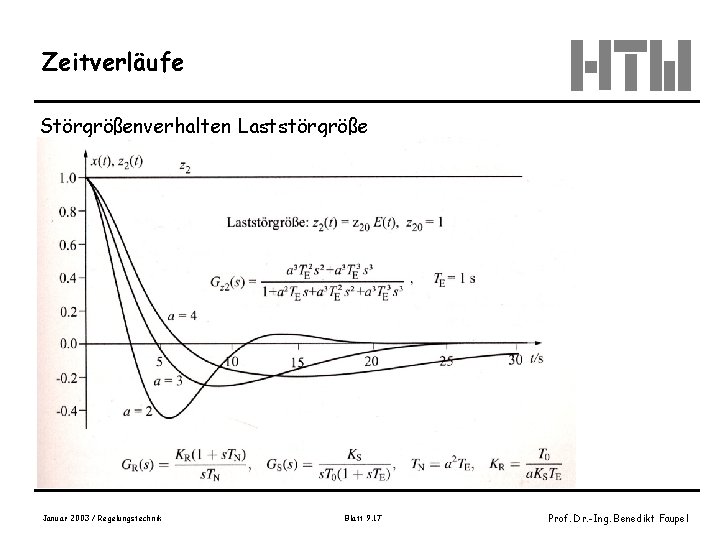
Zeitverläufe Störgrößenverhalten Laststörgröße Januar 2003 / Regelungstechnik Blatt 9. 17 Prof. Dr. -Ing. Benedikt Faupel

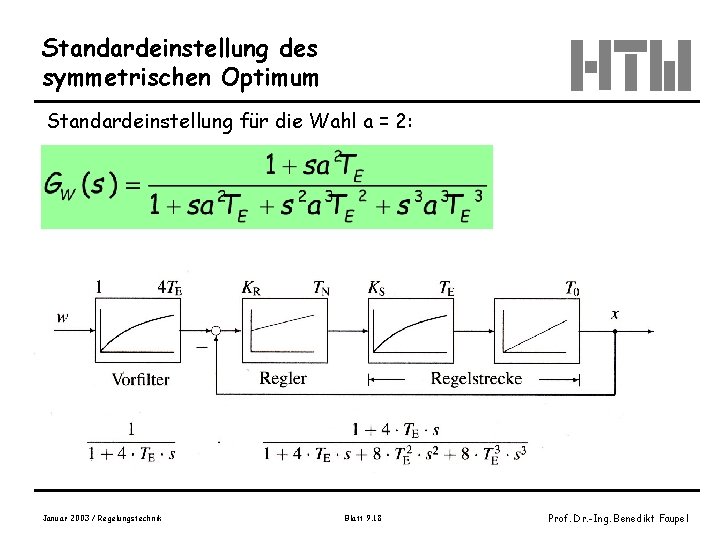
Standardeinstellung des symmetrischen Optimum Standardeinstellung für die Wahl a = 2: Januar 2003 / Regelungstechnik Blatt 9. 18 Prof. Dr. -Ing. Benedikt Faupel

Standardeinstellung des symmetrischen Optimum Standardeinstellung für die Wahl a = 2: Kompensation des D-Anteils durch Vorfilter Januar 2003 / Regelungstechnik Blatt 9. 19 Prof. Dr. -Ing. Benedikt Faupel

Standardeinstellung des symmetrischen Optimum Januar 2003 / Regelungstechnik Blatt 9. 20 Prof. Dr. -Ing. Benedikt Faupel

Standardeinstellung symmetrisches Optimum Tabelle 10. 5 -1, Wendt, S. 428 Bestes Einstellung mit Wahl a = 2 Januar 2003 / Regelungstechnik Blatt 9. 21 Prof. Dr. -Ing. Benedikt Faupel

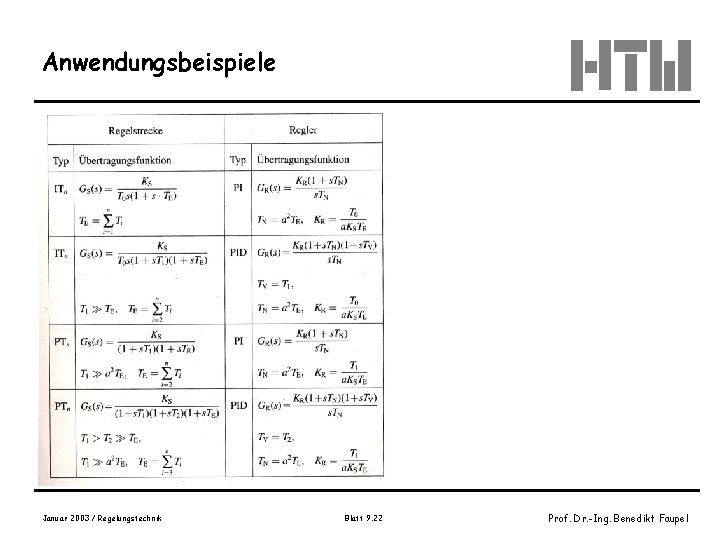
Anwendungsbeispiele Tabelle 10. 5 -2, Wendt, S. 433 Januar 2003 / Regelungstechnik Blatt 9. 22 Prof. Dr. -Ing. Benedikt Faupel

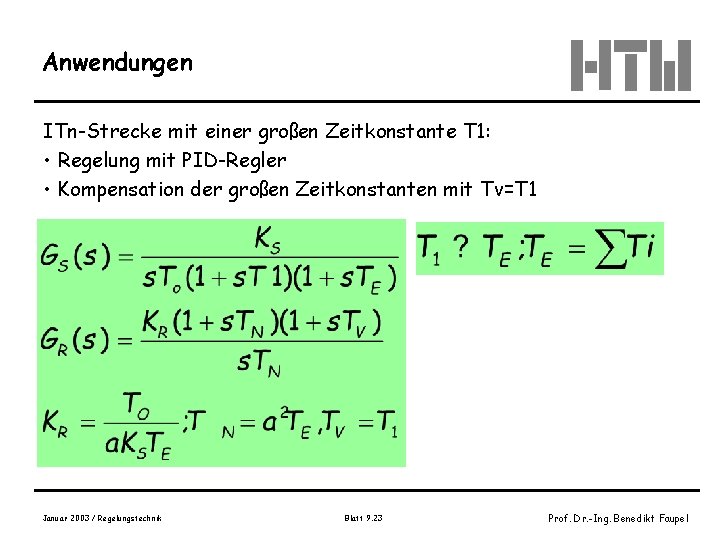
Anwendungen ITn-Strecke mit einer großen Zeitkonstante T 1: • Regelung mit PID-Regler • Kompensation der großen Zeitkonstanten mit Tv=T 1 Januar 2003 / Regelungstechnik Blatt 9. 23 Prof. Dr. -Ing. Benedikt Faupel

Anwendungen ITn-Strecke Übertragungsfunktion offener Regelkreis: Führungsübertragungsfunktion Januar 2003 / Regelungstechnik Blatt 9. 24 Prof. Dr. -Ing. Benedikt Faupel

Anwendungen PTn-Strecke mit einer großen Zeitkonstante T 1: • Regelung mit PI-Regler • Keine Kompensation der großen Zeitkonstanten mit T 1 Januar 2003 / Regelungstechnik Blatt 9. 25 Prof. Dr. -Ing. Benedikt Faupel

Anwendungen PTn-Strecke Übertragungsfunktion offener Regelkreis: FÜhrungsübertragungsfunktion Januar 2003 / Regelungstechnik Blatt 9. 26 Prof. Dr. -Ing. Benedikt Faupel

Anwendungen PTn-Strecke mit zwei großen Zeitkonstante T 1 und T 2: • Regelung mit PID-Regler • Kompensation der zweitgrößten Zeitkonstanten mit Tv=T 2 Januar 2003 / Regelungstechnik Blatt 9. 27 Prof. Dr. -Ing. Benedikt Faupel

Anwendungen PTn-Strecke Übertragungsfunktion offener Regelkreis: FÜhrungsübertragungsfunktion Januar 2003 / Regelungstechnik Blatt 9. 28 Prof. Dr. -Ing. Benedikt Faupel

Beispiel Bild Jaschek, S. 150 Auslegung eines PID-Reglers: Januar 2003 / Regelungstechnik Blatt 9. 29 Prof. Dr. -Ing. Benedikt Faupel

Lösung Betragsoptimum Januar 2003 / Regelungstechnik Blatt 9. 30 Prof. Dr. -Ing. Benedikt Faupel

Lösung Betragsoptimum Januar 2003 / Regelungstechnik Blatt 9. 31 Prof. Dr. -Ing. Benedikt Faupel

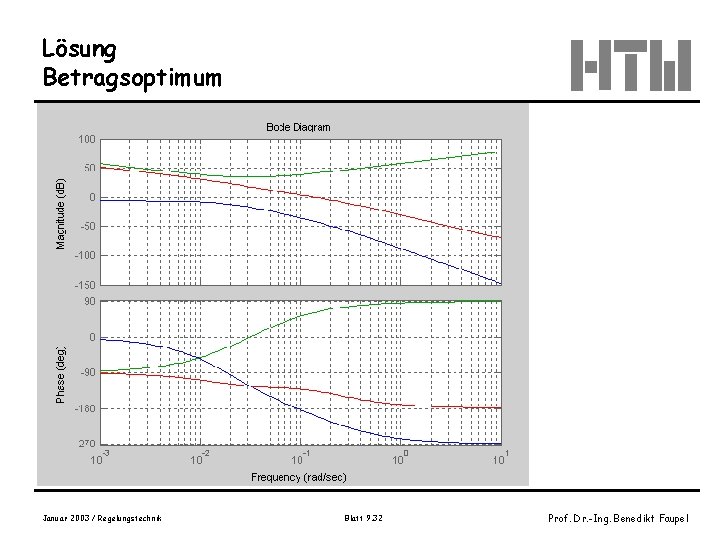
Lösung Betragsoptimum Januar 2003 / Regelungstechnik Blatt 9. 32 Prof. Dr. -Ing. Benedikt Faupel

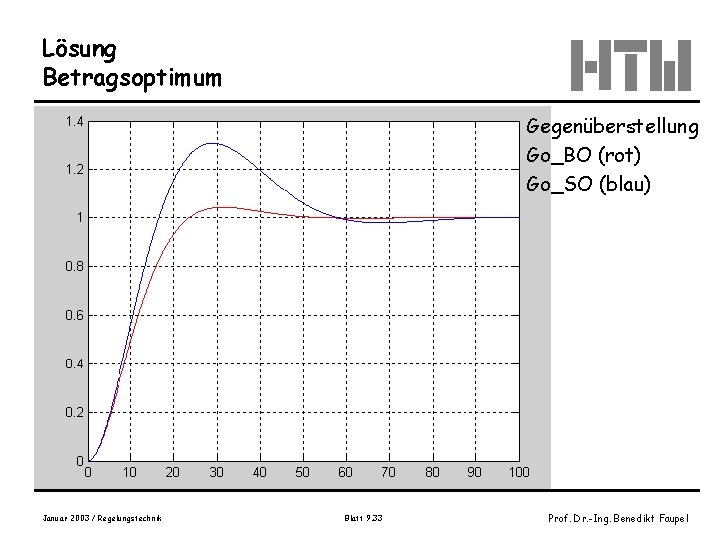
Lösung Betragsoptimum Gegenüberstellung Go_BO (rot) Go_SO (blau) Januar 2003 / Regelungstechnik Blatt 9. 33 Prof. Dr. -Ing. Benedikt Faupel

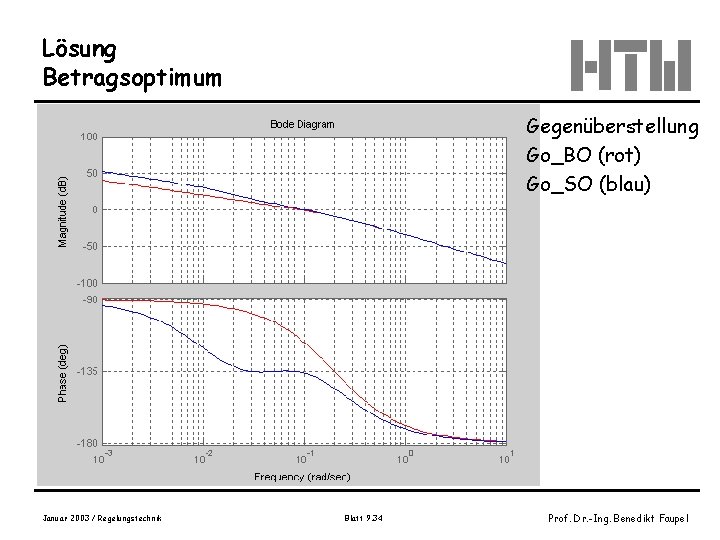
Lösung Betragsoptimum Gegenüberstellung Go_BO (rot) Go_SO (blau) Januar 2003 / Regelungstechnik Blatt 9. 34 Prof. Dr. -Ing. Benedikt Faupel

Gegenüberstellung Betrags- vs. Symmetrisches Optimum Tabelle 10. 5. -3, Wendt, S. 434 Januar 2003 / Regelungstechnik Blatt 9. 35 Prof. Dr. -Ing. Benedikt Faupel

Zusammenfassung Einstellungsregeln Literatur Januar 2003 / Regelungstechnik Blatt 9. 36 Prof. Dr. -Ing. Benedikt Faupel

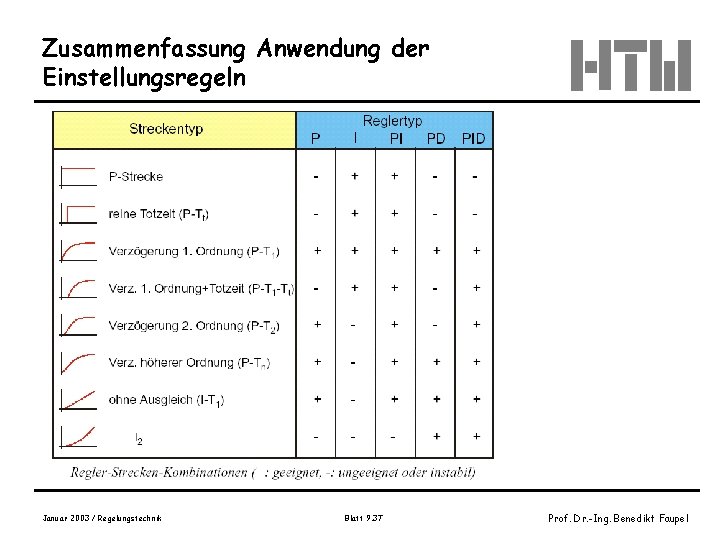
Zusammenfassung Anwendung der Einstellungsregeln Januar 2003 / Regelungstechnik Blatt 9. 37 Prof. Dr. -Ing. Benedikt Faupel