Universit de Rennes 1 Licence Sciences Technologie Sant

Université de Rennes 1 Licence Sciences Technologie Santé L 2 -PCGI Electromagnétisme Philippe Rabiller 2005 Electromagnétisme - L 2 PCGI - Université Rennes 1 - 2005 1

Plan du cours • ch. 1 Introduction • ch. 2 Vecteurs et champs • ch. 3 Champ et Potentiel électrostatiques • ch. 4 Champ Magnétique • ch. 5 Induction électromagnétique • ch. 6 Propagation des ondes électromagnétiques • ch. 7 Rayonnement électromagnétique Electromagnétisme - L 2 PCGI - Université Rennes 1 - 2005 2

Chapitre 4: Champ Magnétique 4. 1 Champ magnétique, loi de Biot et Savart 4. 2 Force magnétique exercée sur un conducteur 4. 3 Le potentiel vecteur 4. 4 Rotationnel du champ magnétique - théorème d’Ampère 4. 5 Utilisation du théorème d’Ampère 4. 6 Dipôle Magnétique 4. 7 Matériaux Magnétiques 4. 8 … 4. 9 … 4. 10 … Electromagnétisme - L 2 PCGI - Université Rennes 1 - 2005 3

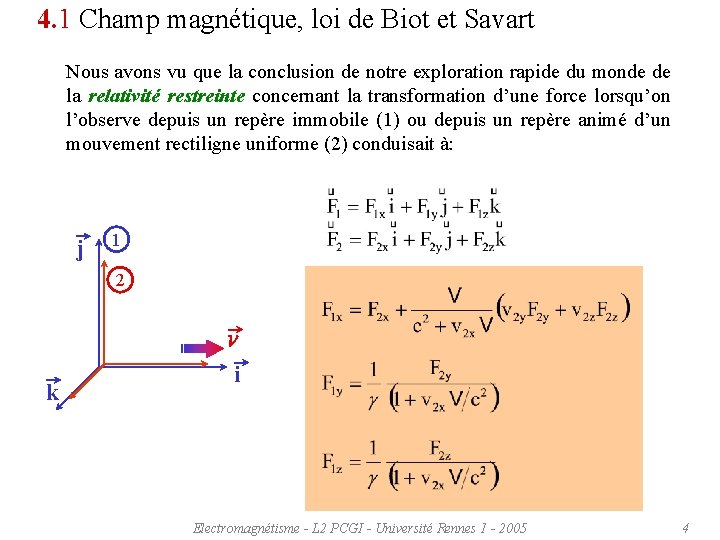
4. 1 Champ magnétique, loi de Biot et Savart Nous avons vu que la conclusion de notre exploration rapide du monde de la relativité restreinte concernant la transformation d’une force lorsqu’on l’observe depuis un repère immobile (1) ou depuis un repère animé d’un mouvement rectiligne uniforme (2) conduisait à: j 1 2 V k i Electromagnétisme - L 2 PCGI - Université Rennes 1 - 2005 4

4. 1 Champ magnétique, loi de Biot et Savart Soit deux charges immobiles dans le repère (2): Q à l’origine et q à la position . Les vitesses v 2 x, v 2 y et v 2 z sont nulles et les forces s’écrivent: j 1 2 r k Q q V i Electromagnétisme - L 2 PCGI - Université Rennes 1 - 2005 5

4. 1 Champ magnétique, loi de Biot et Savart Appliquons maintenant les transformations de Lorentz aux coordonnées. Pour simplifier on prend les deux charges dans le plan (x, y). j 1 2 r k Q q V i Cette expression peut se mettre sous la forme vectorielle: Electromagnétisme - L 2 PCGI - Université Rennes 1 - 2005 6

4. 1 Champ magnétique, loi de Biot et Savart Nous pouvons donc résumer ainsi les conséquences de la relativité restreinte: La force exercée par une particule chargée sur une autre particule, perçue par un observateur dans un repère fixe - alors que les deux charges sont au repos dans un deuxième repère mobile animé d’une vitesse de translation V – ne peut plus s’exprimer simplement par une force radiale. Il est nécessaire d’ajouter une composante perpendiculaire à la première et proportionnelle à la vitesse V. Tout se passe donc comme si on ajoutait un champ supplémentaire: le champ magnétique. 1 F = q E 2 r k Q q q Q r 2 E = 4 eor 23 Dans le repère où les charges sont au repos V eomo=c 2 F = q ( E + V B ) Force de Lorentz g Q r 1 E = 4 eor 13 mo g QV sin(q)k B = 4 r 12 Dans le repère où les charges sont mobiles Electromagnétisme - L 2 PCGI - Université Rennes 1 - 2005 7

4. 1 Champ magnétique, loi de Biot et Savart Voyons à présent comment calculer le champ magnétique créé, non pas par une charge ponctuelle en mouvement, mais par un courant de charges en mouvement. Remplaçons la charge ponctuelle Q par un petit élément de longueur dl d’un circuit électrique dans le plan (x, y) parcouru par un courant I. Ce courant est un débit de charges, c’est à dire une quantité de charge par unité de temps (exprimé en ampères, 1 A=1 Cs-1). n I S V dl Supposons que la section S du conducteur électrique est constante sur toute la longueur et que n est la densité homogène de charges mobiles (de charge La quantité de charge comprise dans l’élément de circuit est élémentaire e). Q = n e S dl et le courant I donné par d. Q/dt vaut donc: I = n e S (dl/dt). Or dl/dt représente la vitesse V des charges en écoulement. Donc en tenant compte du fait qu’en tout point du conducteur dl et V sont parallèles on peut aussi écrire ceci sous la forme : I dl = Q V Electromagnétisme - L 2 PCGI - Université Rennes 1 - 2005 8

4. 1 Champ magnétique, loi de Biot et Savart La vitesse des électrons dans les bons conducteurs électriques peut atteindre plusieurs milliers de kilomètres par seconde, mais reste néanmoins très petite devant la vitesse de la lumière. On peut donc remplacer g par 1 dans la suite du cours. D’autre part l’angle q est l’angle compris entre la direction de r et la direction de V donc de dl. Ces deux vecteurs étant dans le plan (x, y) ils sont perpendiculaires au vecteur unitaire k. On a donc: QV sin(q) k = I dl r sin(q) k / r = I dl r r Et l’élément de champ magnétique d. B créé par l’élément de circuit dl est alors donné par: mo I dl r d. B = 4 r 3 Il s’agit de la loi de Biot et Savart. Dans le système international le champ magnétique s’exprime en Tesla (T), le courant électrique en ampères (A) et les longueurs en mètres (m). La constante mo vaut alors 4 p 10 -7. ! Le vecteur r donne la position de l’endroit où on calcule le champ, par rapport à l’élément de circuit qui est la source de ce champ. Electromagnétisme - L 2 PCGI - Université Rennes 1 - 2005 9

4. 1 Champ magnétique, loi de Biot et Savart Le courant I passant à travers une section d. S, peut être écrit sous la forme du produit de cette section par une densité de courant j: I = j ·d. S. Ainsi pour un élément de circuit de longueur dl et de section d. S, le produit I dl prend la forme (j·d. S) dl = j d 3 r’où d 3 r’représente un élément de volume du circuit générateur de champ magnétique. Et la loi de Biot et Savart se généralise de la manière suivante pour un circuit où le courant électrique I est réparti dans l’espace avec une densité de courant j (r ’). V’ r (r ’) + m B ( r ) = 4 o j (r ’) r (r ’) 3 ’ dr 3 r V’ r ’ Boucles de courants microscopiques dans certains matériaux « MAGNETIQUES » AIMANTS Electromagnétisme - L 2 PCGI - Université Rennes 1 - 2005 10

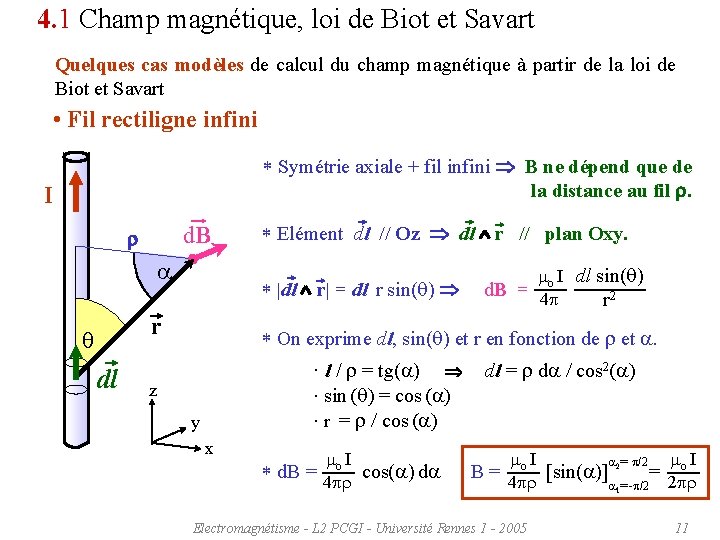
4. 1 Champ magnétique, loi de Biot et Savart Quelques cas modèles de calcul du champ magnétique à partir de la loi de Biot et Savart • Fil rectiligne infini * Symétrie axiale + fil infini B ne dépend que de la distance au fil r. I d. B r a m I dl sin(q) o * |dl r| = dl r sin(q) d. B = 4 r q dl * Elément dl // Oz dl r // plan Oxy. r 2 * On exprime dl, sin(q) et r en fonction de r et a. · l / r = tg(a) dl = r da / cos 2(a) · sin (q) = cos (a) · r = r / cos (a) z y x m I a 2= /2 m I o o o * d. B = cos(a) da B = [sin(a)] = 2 r 4 r a 1=- /2 Electromagnétisme - L 2 PCGI - Université Rennes 1 - 2005 11

4. 1 Champ magnétique, loi de Biot et Savart « Règle du tire-bouchon » mo Rappelons l’expression de la loi de Biot et Savart: d. B = 4 I dl r r 3 Si on regarde dans le sens du courant, les lignes de champ sont: • dans un plan perpendiculaire à l’élément de courant et au point où on calcule le champ • dirigées dans le sens de rotation des aiguilles d’une montre. On peut donc retrouver la direction des lignes de champ en utilisant la règle du tire-bouchon: « le courant avance comme le tire-bouchon tourne dans les sens des lignes de champ» . I Electromagnétisme - L 2 PCGI - Université Rennes 1 - 2005 12

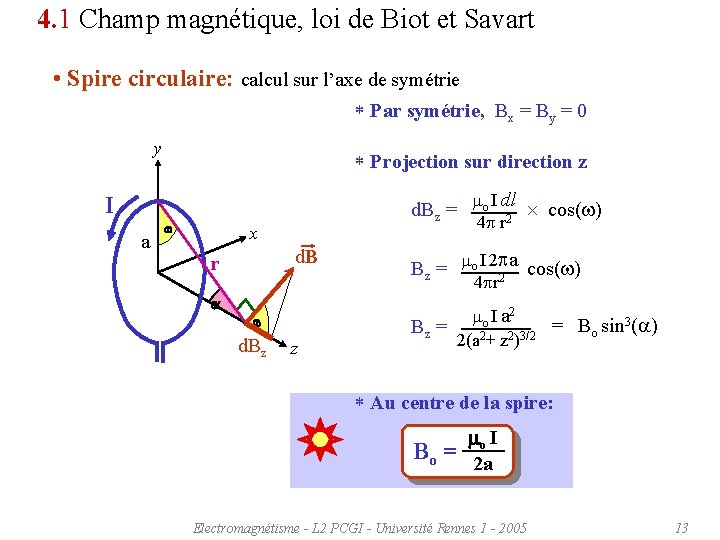
4. 1 Champ magnétique, loi de Biot et Savart • Spire circulaire: calcul sur l’axe de symétrie * Par symétrie, Bx = By = 0 y * Projection sur direction z mo I dl d. Bz = cos(w) 2 I a w 4 r x d. B r a mo I 2 a Bz = cos(w) 2 4 r w d. Bz z mo I a 2 = B sin 3(a) Bz = o 2(a 2+ z 2)3/2 * Au centre de la spire: m I o Bo = 2 a Electromagnétisme - L 2 PCGI - Université Rennes 1 - 2005 13

4. 2 Force magnétique exercée sur un conducteur Plaçons un élément de circuit électrique, de longueur dl et parcouru par un courant électrique I, dans un champ magnétique B. Nous supposons que le champ électrique ambiant est nul et ne nous intéressons donc qu’à la composante de la force magnétique. dl I B ! Ici le champ magnétique et l’élément de circuit qui est soumis au champ sont au même endroit. La force totale exercée par le champ magnétique sur l’élément de longueur dl est la somme de toutes les forces de Lorentz exercées individuellement sur toutes les charges élémentaires, en nombre N = n S dl. F = N q V B = QV B F = I dl B Electromagnétisme - L 2 PCGI - Université Rennes 1 - 2005 14

4. 2 Force magnétique exercée sur un conducteur Le champ crée par un circuit est l’intégrale (la somme) du champ crée par un élément infinitésimal en sommant sur la totalité du circuit. B = mo I 4 dl r r 3 De même, la force exercée par un champ magnétique sur un circuit rigide est l’intégrale de la force exercée sur tout élément infinitésimal et en sommant sur la totalité du circuit. F = I’ dl ’ B Ainsi la force s’exerçant mutuellement entre deux circuits rigides parcourus par des courants I et I’ est donnée par: - + mo I’ I dl ’ ( dl r ) dl F = 4 - + r 3 dl r r d. F I’ dl ’ I Il peut également s’exercer un couple ! Moteurs rotatifs Electromagnétisme - L 2 PCGI - Université Rennes 1 - 2005 15

4. 3 Le potentiel vecteur De même que le champ électrique dérive d’un potentiel électrostatique scalaire, le champ magnétique dérive d’un potentiel vectoriel: le potentiel vecteur. Si l’intérêt de manipuler un champ scalaire plutôt qu’un champ vectoriel est évident dans le cas de l’électrostatique, l’intérêt de manipuler un potentiel vecteur l’est moins à priori, mais permet d’une part de faire un parallèle entre électrostatique et magnétisme et recouvre tout son sens lorsqu’on traite par exemple l’interaction rayonnement matière dans le cadre de la mécanique quantique. Rappelons quatre identités vectorielles. Soit deux vecteurs A et B et une fonction scalaire f. • ( A) = 0 • ( A B) = B • ( A) - A • ( B) (f. A ) = ( f ) A + f ( A) • ( f. A ) = ( f ) • A + f • A Electromagnétisme - L 2 PCGI - Université Rennes 1 - 2005 16

4. 3 Le potentiel vecteur Divergence du champ magnétique : Calculons la divergence du champ magnétique à partir de l’expression généralisée de la loi de Biot et Savart: m • B = 4 o j (r ’) r (r ’) 3 r’ • d r 3 Nous avons pu inverser l’opérateur Nabla et l’intégrale car ces deux opérations agissent sur des coordonnées différentes (Nabla sur « r » et l’intégrale sur « r’ » ). Appliquons ensuite la deuxième identité vectorielle au terme de droite de l’équation: • ( A B) = B • ( A) - A • ( B) r • j - j • r r • j = r 3 r 3 0 Le premier terme de droite de l’équation est nul car agit sur des fonctions de r et j ne dépend que de r’. Electromagnétisme - L 2 PCGI - Université Rennes 1 - 2005 17

4. 3 Le potentiel vecteur Divergence du champ magnétique : Pour calculer le second terme, rappelons que agit sur des fonctions de r, indépendamment de r’. On peut donc, pour simplifier, faire le calcul pour la valeur particulière r’=0. Plaçons nous dans un repère cartésien: r 2 = x 2 + y 2 + z 2 z y r 3 y z r 3 x r = z r 3 z x r 3 y x r 3 x y r 3 -3 zy z z = = y (x 2+y 2+z 2)3/2 y r 3 -3 yz y y = = z (x 2+y 2+z 2)3/2 z r 3 + permutations circulaires Electromagnétisme - L 2 PCGI - Université Rennes 1 - 2005 r = 0 r 3 18

4. 3 Le potentiel vecteur Divergence du champ magnétique : Finalement, nous venons de montrer que la divergence du champ magnétique est nulle. • B = 0 Potentiel vecteur : Rappelons maintenant la première des identités vectorielles • ( A) = 0 Nous voyons que nous pouvons toujours définir le champ magnétique comme étant le rotationnel d’un autre vecteur que nous appellerons Potentiel Vecteur. Le potentiel vecteur n’est défini qu’à un vecteur près dont le rotationnel est nul ! On parle alors de choix de jauge. A C = ( + ) A + C = A si Electromagnétisme - L 2 PCGI - Université Rennes 1 - 2005 C = 0 19

4. 3 Le potentiel vecteur Potentiel vecteur : Pour calculer le potentiel vecteur, nous repartons de l’expression générale du champ magnétique et utilisons la troisième identité vectorielle: (f. A ) = ( f ) A + f ( A) m B ( r ) = 4 o j (r ’) r (r ’) 3 ’ dr 3 r 1 r Mais avant, faisons apparaître le terme sous une forme différente : - r r 3 1 r = 1 x (x 2+y 2+z 2)1/2 x r 3 1 y (x 2+y 2+z 2)1/2 = - y 3 r z r 3 1 z (x 2+y 2+z 2)1/2 = - Electromagnétisme - L 2 PCGI - Université Rennes 1 - 2005 r r 3 20

4. 3 Le potentiel vecteur Potentiel vecteur : On peut donc écrire le champ magnétique sous la forme: mo 1 B ( r ) = j (r ’) d 3 r’ 4 r Or 1 r j = j r - 1 r j (r ’) 0 mo j (r ’) 3 r’ Ce qui conduit pour le champ magnétique à: B ( r ) = d 4 r On aboutit donc à la définition du potentiel vecteur (après inversion de « Nabla » et du « Signe Somme » : mo j (r ’) 3 ’ A ( r ) = d r 4 r Electromagnétisme - L 2 PCGI - Université Rennes 1 - 2005 21

4. 3 Le potentiel vecteur Parallèle avec le potentiel électrostatique : Replaçons nous dans la même géométrie que celle adoptée pour l’étude du potentiel électrostatique: 1 V( r ) = 4 eo r - r ’ r r( r ’)d 3 r’ | r - r ’| Scalaire !!! - V( r ) = E( r ) + mo j ( r ’) 3 ’ A ( r ) = d r 4 | r - r ’| Vectoriel !!! A( r ) = B( r ) ! Ces lois ne sont vraies, sous cette forme, que dans le cas statique. Nous verrons qu’il faut les compléter en électrodynamique… Electromagnétisme - L 2 PCGI - Université Rennes 1 - 2005 22

4. 4 Rotationnel du champ magnétique - théorème d’Ampère En électromagnétisme il y a le théorème de Gauss qui relie le flux du champ électrique à travers une surface fermée à la charge électrostatique totale contenue dans le volume délimité par la dite surface. d. S qi S E = E·d. S = eo Qtotal E Q eo V SV De la même manière il existe un autre théorème que nous allons démontrer - le théorème d’Ampère - qui relie la circulation du champ magnétique le long d’un contour au courant total traversant la surface s’appuyant sur ce contour. L CB = B·dl = mo Ii = mo Itotal Electromagnétisme - L 2 PCGI - Université Rennes 1 - 2005 B dl I SG G 23

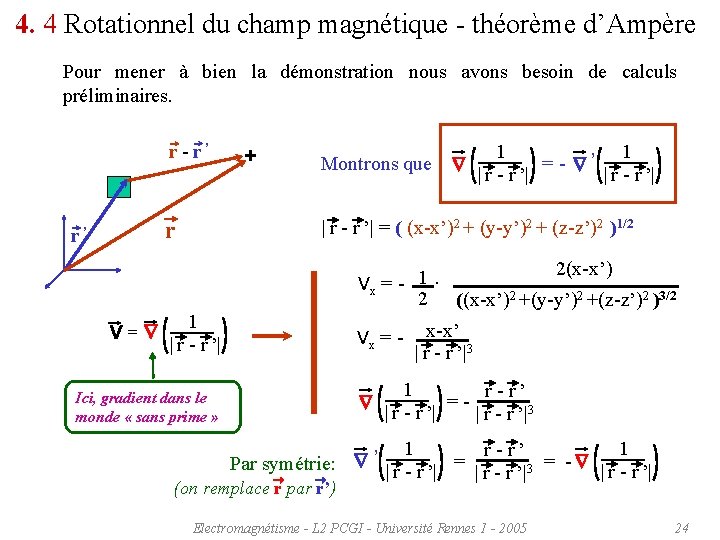
4. 4 Rotationnel du champ magnétique - théorème d’Ampère Pour mener à bien la démonstration nous avons besoin de calculs préliminaires. r - r ’ r r ’ V = + 1 1 Montrons que = - ’ | r - r ’| = ( (x-x’)2 + (y-y’)2 + (z-z’)2 )1/2 1 | r - r ’| Ici, gradient dans le monde « sans prime » 2(x-x’) 1 Vx = - · 2 ((x-x’)2 +(y-y’)2 +(z-z’)2 )3/2 Vx = x-x’ | r - r ’|3 1 r - r ’ = | r - r ’|3 1 1 r - r ’ ’ = = - | r - r ’| Par symétrie: | r - r ’|3 (on remplace r par r’) Electromagnétisme - L 2 PCGI - Université Rennes 1 - 2005 24

4. 4 Rotationnel du champ magnétique - théorème d’Ampère Montrons à présent que ·A = 0 pour une distribution de charge statique. mo j ( r ’) 3 ’ r ·A ( r ) = · d 4 | r - r ’| • ( f. A ) = ( f ) • A + f • A j ( r ’) 1 1 · = ·j ( r ’) + j ( r ’) · | r - r ’| 0 Remplaçons le gradient en « r » par son homologue en « r’» . j ( r ’) 1 1 ’ · = ’·j ( r ’) + j ( r ’) · ’ | r - r ’| 1 1 ’ Et utilisons l’égalité: = | r - r ’| Electromagnétisme - L 2 PCGI - Université Rennes 1 - 2005 25

4. 4 Rotationnel du champ magnétique - théorème d’Ampère ’ j ( r ) j ( r ’) 1 · = ’·j ( r ’) - ’ · | r - r ’| Nous obtenons alors: j ( r ’) 3 ’ mo mo 1 3 ’ ’ dr ·A ( r ) = d ’·j ( r ) r - ’ · 4 4 | r - r ’| ’·j ( r ’) exprime la loi de conservation de la charge et vaut donc -dr(r ’)/dt. V d 3 r = d V V = d V /d 3 r Théorème de la divergence intégrale de surface contenant tous les courants. A la surface le courant est alors nul ou tangent à la surface. Donc l’intégrale est nulle. V = j [j] = charge/unité de temps/unité surface d j /d 3 r (charge /unité volume )/unité de temps r ( r ’) 3 ’ 1 -moeo On a donc : ·A ( r ) = d r t 4 eo | r - r ’| = -1 c 2 Electromagnétisme - L 2 PCGI - Université Rennes 1 - 2005 V ( r ) t 26

4. 4 Rotationnel du champ magnétique - théorème d’Ampère Nous retrouvons, via les potentiels vecteur et électrostatique, que magnétisme et électrostatique sont bien deux grandeurs liées, ce que nous avait appris l’introduction à la relativité restreinte. 1 V ( r ) ·A ( r ) + = 0 c 2 t Dans le cas de courants continus, ou régime stationnaire, le potentiel électrostatique ne dépend pas du temps et la divergence du potentiel vecteur est nulle, ce que nous cherchions à démontrer. V ( r ) t = 0 Rotationnel du champ magnétique : ·A ( r ) = 0 B = ( A) Nous allons, une nouvelle fois, utiliser une identité que nous ne démontrerons pas ici (mais que vous pouvez vérifier vous même). ( A) = ( ·A) - 2 A vecteur 0 vecteur 2 Ax 2 Ay 2 Az Electromagnétisme - L 2 PCGI - Université Rennes 1 - 2005 27

4. 4 Rotationnel du champ magnétique - théorème d’Ampère Reprenant l’expression du potentiel vecteur trouvée précédemment et notant encore une fois que l’opérateur Nabla n’agit que sur les coordonnées en « r » , on peut donc écrire le rotationnel du champ magnétique sous la forme: mo B = - A = - 4 j(r ) 2 2 Il faut donc calculer 2 1 | r - r ’| = · 2 j ( r ’) 3 ’ dr | r - r ’| ’ 2 1 | r - r ’| d 3 r’ 1 = · 1 | r - r ’| R Où pour alléger l’écriture nous posons: R = | r - r ’| = (x-x’)2 + (y-y’)2 + (z-z’)2 1/2 = X 2 + Y 2 + Z 2 1/2 Et donc les opérations de dérivées seront en " / X " etc. Electromagnétisme - L 2 PCGI - Université Rennes 1 - 2005 28

4. 4 Rotationnel du champ magnétique - théorème d’Ampère Calculons la composante suivant X de 1 X R 1 R -X = = R 3 X 2 + Y 2 + Z 2 1/2 X 2 + Y 2 + Z 2 3/2 1 - (1/2) 2 X De même pour les composantes suivant Y et Z de 1 Y R 1 Z R = 1 Y X 2 + Y 2 + Z 2 1/2 = 1 Z X 2 + Y 2 + Z 2 1/2 1 R - (1/2) 2 Y = X 2 + Y 2 + Z 2 3/2 = -Y R 3 - (1/2) 2 Z = X 2 + Y 2 + Z 2 3/2 = -ZR 3 On aurait pu déduire les deux dernières expressions par permutations circulaires. . . Le laplacien est alors donné par la divergence du vecteur que nous venons de trouver: 2 = · 1 = -X 3 X R | r - r ’| R 1 -Y -Z + Y R 3 + Z R 3 Electromagnétisme - L 2 PCGI - Université Rennes 1 - 2005 29

4. 4 Rotationnel du champ magnétique - théorème d’Ampère Calculons la composante suivant X du laplacien : - X X R 3 = - X X X 2 + Y 2 + Z 2 3/2 = - X 2 + Y 2 + Z 2 3/2 - X (3/2) 2 X X 2 + Y 2 + Z 2 1/2 X 2 + Y 2 + Z 2 3 2 X 2 - Y 2 - Z 2 X = X R 3 R 5 Et par permutation circulaire : 2 1 | r - r ’| = 2 2 X 2 - Y 2 - Z 2 + -X 2 + 2 Y 2 - Z 2 + -X 2 - Y 2 +2 Z 2 R 5 1 | r - r ’| = 0 Sauf pour r = r’ !!! Electromagnétisme - L 2 PCGI - Université Rennes 1 - 2005 30

4. 4 Rotationnel du champ magnétique - théorème d’Ampère En conclusion cette expression du rotationnel du champ magnétique, sous forme intégrale, n’a de sens que localement, c’est à dire pour r’ r !!! j(r ) mo B = - A = - 4 ’ 2 2 1 | r - r ’| d 3 r’ Soit alors un petit volume V ’entourant r et suffisamment petit pour considérer j( r’) homogène sur ce volume - donc égal à j( r) - et qui peut être sorti de l’intégrale. Comme nous l’avions vu pour le gradient de 1/|r-r’|, nous avons l’égalité suivante pour les laplaciens dans les mondes en « r » et « r’» : 2 1 | r - r ’| = - ’ 2 1 | r - r ’| On a alors pour le rotationnel du champ magnétique: mo j ( r ) B = 4 En « r » ! V ’ 2 1 | r - r ’| d 3 r’ En « r ’ » ’ tend vers zéro autour de la position r où on regarde le champ magnétique B Electromagnétisme - L 2 PCGI - Université Rennes 1 - 2005 31

4. 4 Rotationnel du champ magnétique - théorème d’Ampère Appliquons le théorème de la divergence à l’équation obtenue: mo j ( r ) B = 4 ’ 2 V ’ 1 | r - r ’| d 3 r’ 1 ’ 2 | r - r ’| = ’· ’ 1 | r - r ’| ’ | r - r 1 ’| ·d. S S’ B = mo j ( r ) 4 S’ ( r - r ’) | r - r ’|3 d. S R 2 ·d. S S ’ est une petite surface entourant r. On peut donc prendre une sphère et R = r-r’ est parallèle à d. S Or d. S en coordonnées sphériques est égal à R 2 sin(q)dq dj. Donc l’intégrale vaut 4 p. Electromagnétisme - L 2 PCGI - Université Rennes 1 - 2005 32

4. 4 Rotationnel du champ magnétique - théorème d’Ampère On aboutit donc après ces quelques étapes de calcul à l’expression locale du théorème d’Ampère: B( r ) = mo j ( r ) ! Expression valable uniquement en régime stationnaire et pour des matériaux non magnétiques !!! Nous pouvons alors intégrer le rotationnel du champ magnétique, ainsi que la densité de courant sur toute une surface: B( r ) ·d. S = m j ( r ) d. S o S S Courant traversant la surface S Théorème de Stokes B( r )·dl = m I C o Théorème d’Ampère Electromagnétisme - L 2 PCGI - Université Rennes 1 - 2005 33

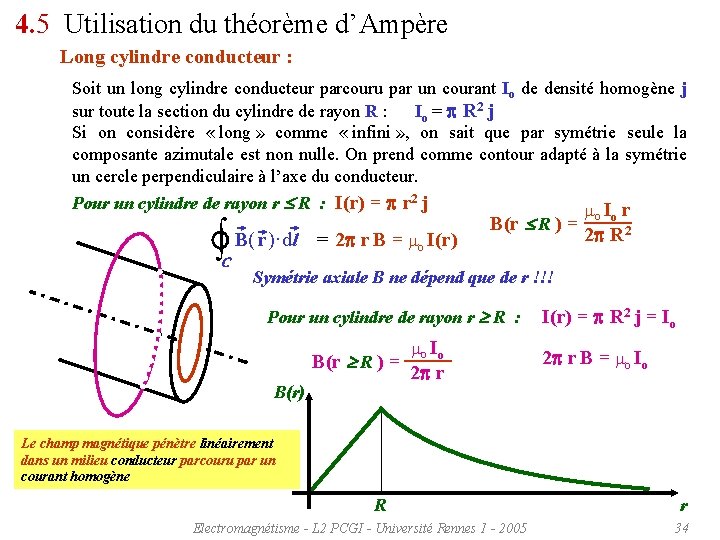
4. 5 Utilisation du théorème d’Ampère Long cylindre conducteur : Soit un long cylindre conducteur parcouru par un courant Io de densité homogène j sur toute la section du cylindre de rayon R : Io = p R 2 j Si on considère « long » comme « infini » , on sait que par symétrie seule la composante azimutale est non nulle. On prend comme contour adapté à la symétrie un cercle perpendiculaire à l’axe du conducteur. Pour un cylindre de rayon r R : I(r) = p r 2 j mo Io r B(r R ) = 2 p R 2 B( r )·dl = 2 p r B = mo I(r) C Symétrie axiale B ne dépend que de r !!! Pour un cylindre de rayon r R : B(r R ) = B(r) mo Io 2 p r I(r) = p R 2 j = Io 2 p r B = mo Io Le champ magnétique pénètre linéairement dans un milieu conducteur parcouru par un courant homogène R Electromagnétisme - L 2 PCGI - Université Rennes 1 - 2005 r 34

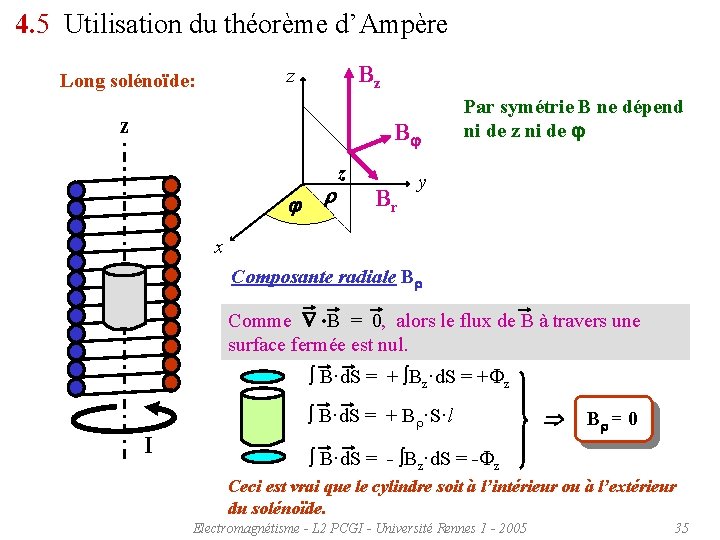
4. 5 Utilisation du théorème d’Ampère Bz z Long solénoïde: z Bj j r z Br Par symétrie B ne dépend ni de z ni de j y x Composante radiale Br • B = 0 Comme , alors le flux de B à travers une surface fermée est nul. B·d. S = + Bz·d. S = + z B·d. S = + Br·S·l I Br = 0 B·d. S = - Bz·d. S = - z Ceci est vrai que le cylindre soit à l’intérieur ou à l’extérieur du solénoïde. Electromagnétisme - L 2 PCGI - Université Rennes 1 - 2005 35

4. 5 Utilisation du théorème d’Ampère Long solénoïde: Composante azimutale Bj La circulation du champ magnétique le long d’un contour du type C (de rayon r) où C’ donne: z B·dl = 2 r. B C C j • A l’intérieur du solénoïde, le contour C n’est traversé par aucun courant et donc Bj=0 partout à l’intérieur. C’ • Le contour C’ est traversé une fois par le courant I et donc à l’extérieur du solénoïde la composante azimutale est donnée par I (sauf si le pas de l’hélice est nul, auquel cas le contour n’est traversé par aucun courant) : Bj = mo. I /2 r à l’extérieur Electromagnétisme - L 2 PCGI - Université Rennes 1 - 2005 36

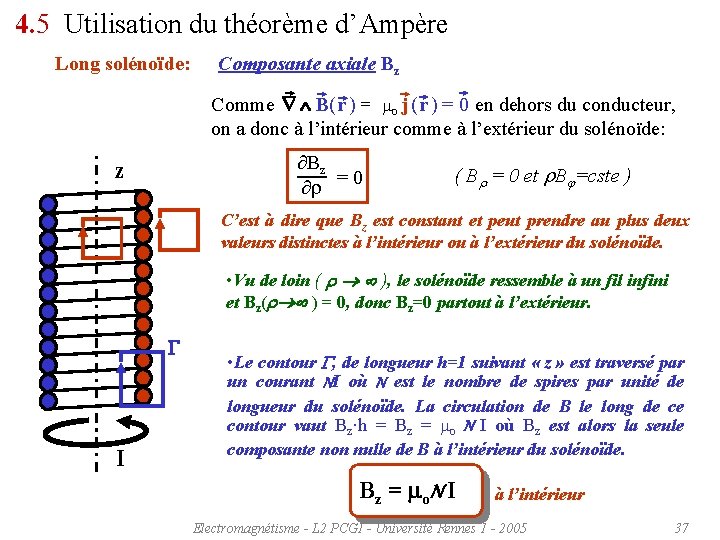
4. 5 Utilisation du théorème d’Ampère Long solénoïde: Composante axiale Bz B( r ) = mo j ( r ) = 0 Comme en dehors du conducteur, on a donc à l’intérieur comme à l’extérieur du solénoïde: Bz = 0 r z ( Br = 0 et r. Bj=cste ) C’est à dire que Bz est constant et peut prendre au plus deux valeurs distinctes à l’intérieur ou à l’extérieur du solénoïde. • Vu de loin ( r ), le solénoïde ressemble à un fil infini et Bz(r ) = 0, donc Bz=0 partout à l’extérieur. G I • Le contour G, de longueur h=1 suivant « z » est traversé par un courant NI où N est le nombre de spires par unité de longueur du solénoïde. La circulation de B le long de ce contour vaut Bz·h = Bz = mo N I où Bz est alors la seule composante non nulle de B à l’intérieur du solénoïde. Bz = mo. N I à l’intérieur Electromagnétisme - L 2 PCGI - Université Rennes 1 - 2005 37

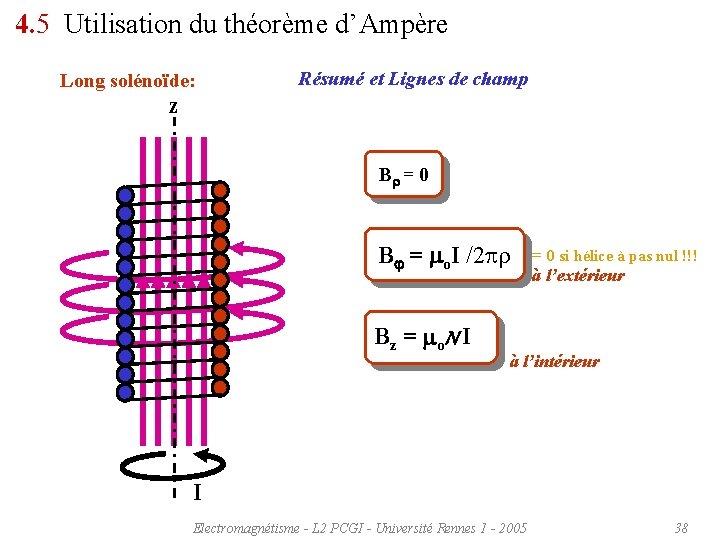
4. 5 Utilisation du théorème d’Ampère Long solénoïde: Résumé et Lignes de champ z Br = 0 Bj = mo. I /2 r Bz = mo. N I = 0 si hélice à pas nul !!! à l’extérieur à l’intérieur I Electromagnétisme - L 2 PCGI - Université Rennes 1 - 2005 38

4. 6 Dipôle Magnétique • De même que la notion de développement multipolaire est importante et en particulier celle de dipôle électrique car souvent utilisée pour modéliser le comportement de la matière au point de vue électrique, il est important également de faire apparaître la notion de dipôle magnétique, d’autant que les « monopôles » magnétiques n’existent pas. • Comme dans le cas électrique, la notion de dipôle magnétique fait référence à une situation où l’observation du champ magnétique ou du potentiel vecteur se fait loin du circuit qui leur donne naissance. • Cette description est tout à fait adaptée lorsqu’on s’intéresse par exemple aux propriétés magnétiques des atomes où les électrons gravitant autour des noyaux constituent des boucles microscopiques de courant (diamagnétisme et paramagnétisme électronique). Electromagnétisme - L 2 PCGI - Université Rennes 1 - 2005 39

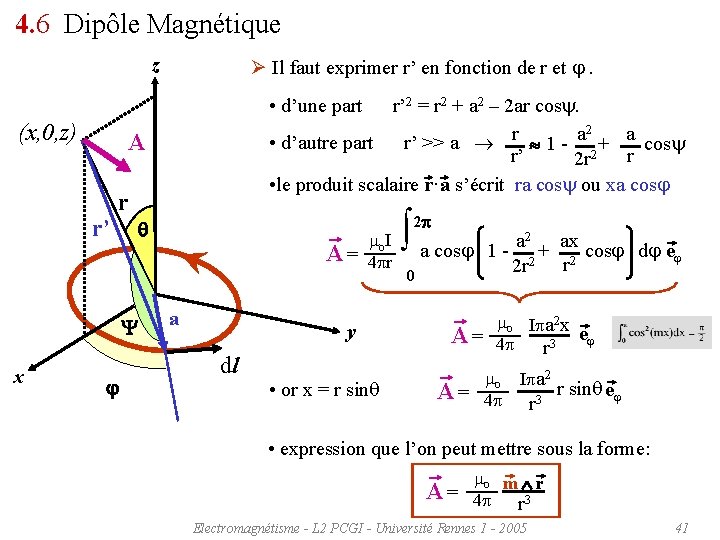
4. 6 Dipôle Magnétique Intéressons nous à la boucle de courant ci dessous, et plus particulièrement au calcul du potentiel vecteur au point (x, 0, z). z (x, 0, z) A r’ r q x Le plan x. Oz est un plan de symétrie et pour tout élément dl à l’azimut j, il existe un autre élément à l’azimut –j de telle sorte que les composantes du potentiel vecteur s’ajoutent suivant y et s’annulent suivant x. j Soit ej le vecteur unitaire parallèle à dl pour l’azimut j. a y dl mo j (r ’) 3 ’ A ( r ) = d r 4 r j(r’)d 3 r’ = I dl = I a dj ej m. I A = 4 o 2 p 0 a cosj dj ej r ’ Electromagnétisme - L 2 PCGI - Université Rennes 1 - 2005 40

4. 6 Dipôle Magnétique z (x, 0, z) • d’une part r’ 2 = r 2 + a 2 – 2 ar cos. 2 r a a • d’autre part r’ >> a 1 - + cos r r’ 2 r 2 • le produit scalaire r·a s’écrit ra cos ou xa cosj A r’ r q x Ø Il faut exprimer r’ en fonction de r et j. j mo I A = 4 r a y dl • or x = r sinq a cosj dj a ax e 1 - + cosj 2 p 0 2 2 r 2 j mo I a 2 x A = 4 r 3 ej mo I a 2 A = 4 r 3 r sinq ej • expression que l’on peut mettre sous la forme: mo m r A = 4 r 3 Electromagnétisme - L 2 PCGI - Université Rennes 1 - 2005 41

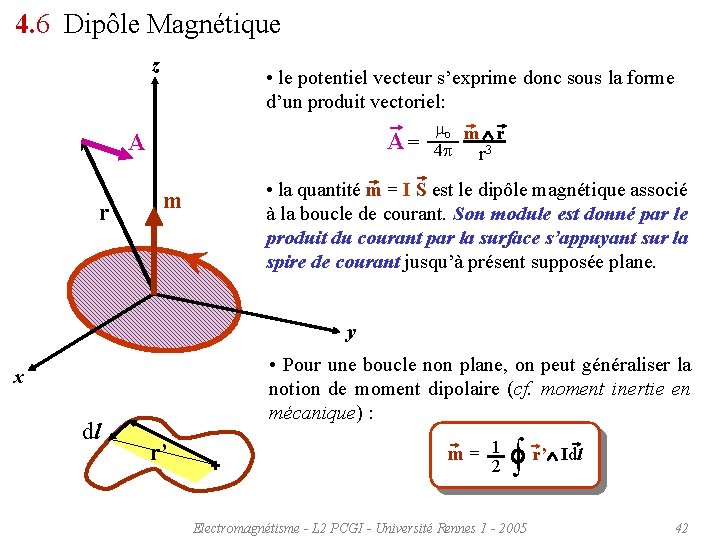
4. 6 Dipôle Magnétique z • le potentiel vecteur s’exprime donc sous la forme d’un produit vectoriel: mo m r A = 4 r 3 A r • la quantité m = I S est le dipôle magnétique associé à la boucle de courant. Son module est donné par le produit du courant par la surface s’appuyant sur la spire de courant jusqu’à présent supposée plane. m y • Pour une boucle non plane, on peut généraliser la notion de moment dipolaire (cf. moment inertie en mécanique) : x dl r’ + 1 m = r’ Idl 2 Electromagnétisme - L 2 PCGI - Université Rennes 1 - 2005 42

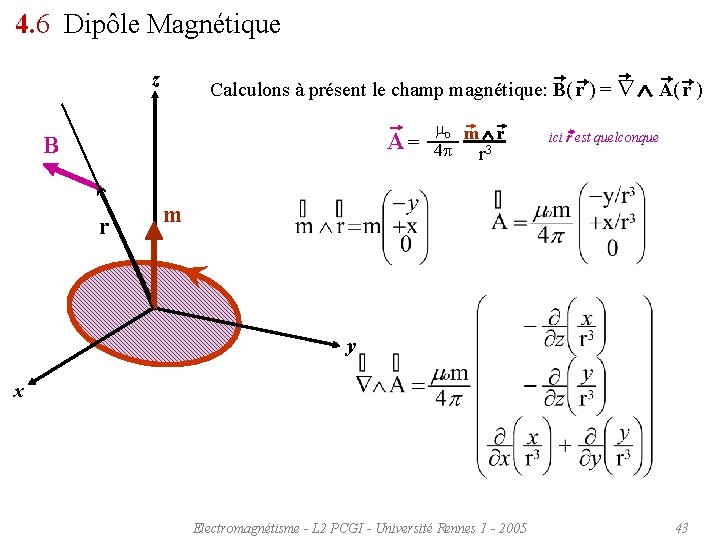
4. 6 Dipôle Magnétique z Calculons à présent le champ magnétique: B( r ) = A( r ) mo m r A = 4 r 3 B r ici r est quelconque m y x Electromagnétisme - L 2 PCGI - Université Rennes 1 - 2005 43

4. 6 Dipôle Magnétique Electromagnétisme - L 2 PCGI - Université Rennes 1 - 2005 44

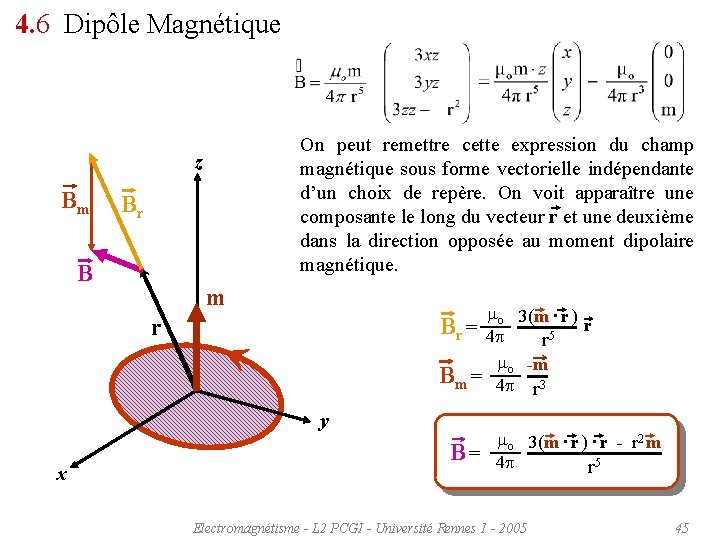
4. 6 Dipôle Magnétique On peut remettre cette expression du champ magnétique sous forme vectorielle indépendante d’un choix de repère. On voit apparaître une composante le long du vecteur r et une deuxième dans la direction opposée au moment dipolaire magnétique. z Bm Br B m mo 3(m · r ) r Br = 4 5 r m -m Bm = 4 o r 3 r y x mo 3(m · r ) · r - r 2 m B = 4 r 5 Electromagnétisme - L 2 PCGI - Université Rennes 1 - 2005 45

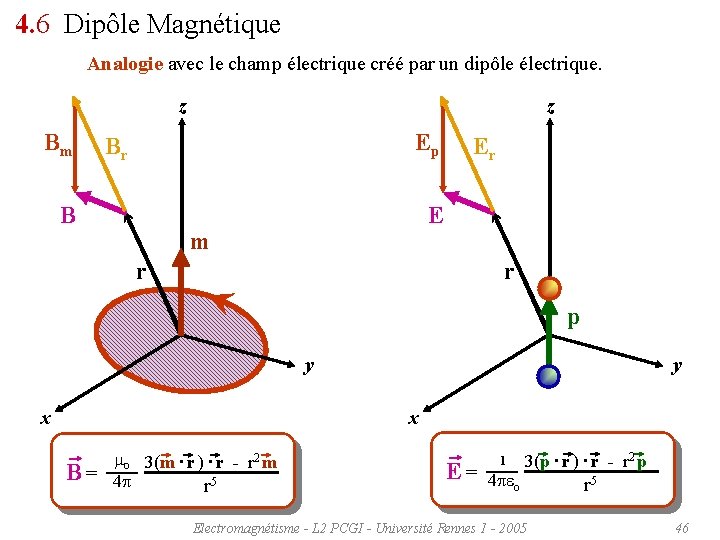
4. 6 Dipôle Magnétique Analogie avec le champ électrique créé par un dipôle électrique. z Bm z Ep Br B Er E m r r p y x mo 3(m · r ) · r - r 2 m B = 4 r 5 E = 1 4 eo 3(p · r ) · r - r 2 p Electromagnétisme - L 2 PCGI - Université Rennes 1 - 2005 r 5 46

4. 7 Matériaux Magnétiques Dans les substances « magnétiques » il existe des « boucles de courant microscopiques » qui donnent naissance à des dipôles magnétiques. Ces dipôles peuvent s’ajouter de façon constructive et la matière devenir ainsi « aimantée » . Si N est la concentration en dipôles magnétiques m par unité de volume, on définit alors l’aimantation M par unité de volume par : M = N m Le potentiel vecteur produit par un élément de volume d 3 r’ est alors donné par: mo M ( r - r’ ) 3 d r’ d. A = 4 3 | r - r’ | Et comme on a déjà montré que: Le potentiel vecteur total vaut: ’ 1 r - r ’ = | r - r ’|3 m 1 o 3 r’ M ’ A ( r ) = d 4 | r - r’ | Electromagnétisme - L 2 PCGI - Université Rennes 1 - 2005 47

4. 7 Matériaux Magnétiques On peut ramener la précédente intégrale en volume en une somme de deux intégrales, l’une de surface et l’autre en volume faisant apparaître des densités équivalentes de courant en surface e et volume je: m 1 o 3 r’ M ’ A ( r ) = d 4 | r - r’ | Pour cela on va utiliser des identités, devenues familières (ou presque) : (f. A ) = ( f ) A + f ( A) • ( A B) = B • ( A) - A • ( B) La première nous permet la séparation en deux intégrales: -m m ’ M M o o 3 r’ + d 3 r’ ’ A ( r ) = d 4 4 | r - r’ | Electromagnétisme - L 2 PCGI - Université Rennes 1 - 2005 48

4. 7 Matériaux Magnétiques Dans la deuxième intégrale de la partie droite de l’équation, on reconnaît la forme de la définition générale du potentiel vecteur, à condition de poser: je = ’ M Pour faire apparaître une expression similaire pour la première intégrale on utilise l’identité suivante, où le vecteur C est un vecteur constant et le vecteur M = M/|r-r’|: • ( M C) = C • ( M) - M • ( C) 0 Le théorème de la divergence nous permet de passer d’une intégrale de volume à une intégrale de surface: Electromagnétisme - L 2 PCGI - Université Rennes 1 - 2005 49

4. 7 Matériaux Magnétiques Ceci doit être vrai quelque soit le vecteur C constant, donc les deux intégrales entre parenthèses sont égales: On a donc finalement, en posant: e = M n où n est le vecteur normal à la surface en tout point je mo mo e + d 3 r’ A ( r ) = d. S’ 4 4 | r - r’ | e et je sont des densités de courants dits « Ampériens » , à ne pas confondre avec les courants « libres » générés par la mise en mouvement des porteurs de charge libres sous l’action d’un champ électrique externe. Electromagnétisme - L 2 PCGI - Université Rennes 1 - 2005 50

4. 7 Matériaux Magnétiques Champ magnétique auxiliaire: s’il existe simultanément des courants de charges libres et des courants équivalents ampériens (matière aimantée), le théorème d’Ampère est toujours applicable. Dans la version « locale » , avec jl et je les densités de courant libre et équivalente, le théorème d’Ampère s’écrit donc: B( r ) = mo ( jl ( r ) + je ( r ) ) En rappelant l’expression de la densité de courant équivalente en fonction de je = M l’aimantation on aboutit à: M r ) ) B( r ) = mo ( jl ( r ) + ( B( r ) - M = j ( ) l ( r ) mo B - M Nous introduisons alors la quantité que nous appellerons H = mo champ magnétique auxiliaire. Electromagnétisme - L 2 PCGI - Université Rennes 1 - 2005 51

4. 7 Matériaux Magnétiques Le théorème d’Ampère prend donc une forme n’impliquant que les courants de charges libres lorsque’il est exprimé en fonction du champ magnétique auxiliaire: H( r ) = jl ( r ) H( r )·dl = I l Et sans rentrer dans le détail de l’origine microscopique des dipôles magnétiques, on peut traiter l’aimantation d’un matériau aimanté dans le cadre de la Réponse Linéaire, c’est à dire qu’on écrit que la réponse « Aimantation » est proportionnelle à l’excitation « champ magnétique » : B = mo(H + M) M = m H B = m H = mo(1+ m ) H = mo mr H m s’appelle la susceptibilité magnétique et mr la perméabilité relative. Electromagnétisme - L 2 PCGI - Université Rennes 1 - 2005 52

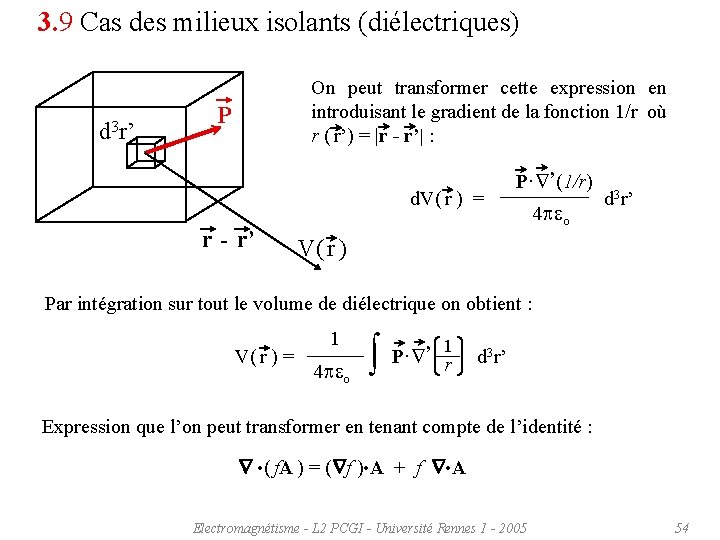
3. 9 Cas des milieux isolants (diélectriques) Dans les milieux isolants, les charges ne sont pas libres de se déplacer « indéfiniment » lorsqu’elles sont soumises à un champ électrique. Elles sont liées à des « centres attracteurs » et ne peuvent s’écarter plus d’une certaine distance de ces attracteurs, entraînant cependant localement la formation de petits dipôles électriques. Supposons un matériaux homogène de volume donné où ces dipôles de moment dipolaire p sont en concentration n. Le moment dipolaire total P ou Polarisation Electrique de l’échantillon « par unité de volume » vaut: P = np d 3 r’ P r - r’ Le potentiel électrostatique créé par unité de volume est alors donné par : P·(r - r’) 3 r’ d. V( r ) = d 4 eo |r - r’|3 V( r ) valable « loin » du diélectrique !!! Electromagnétisme - L 2 PCGI - Université Rennes 1 - 2005 53

3. 9 Cas des milieux isolants (diélectriques) d 3 r’ On peut transformer cette expression en introduisant le gradient de la fonction 1/r où r ( r’) = |r - r’| : P r - r’ P· ’(1/r) d. V( r ) = d 3 r’ 4 eo V( r ) Par intégration sur tout le volume de diélectrique on obtient : 1 V( r ) = 4 eo 1 3 r’ P· ’ d r Expression que l’on peut transformer en tenant compte de l’identité : • ( f. A ) = ( f ) • A + f • A Electromagnétisme - L 2 PCGI - Université Rennes 1 - 2005 54

3. 9 Cas des milieux isolants (diélectriques) En posant f= 1/r on obtient : 1 V( r ) = 4 eo P 1 3 r’ - ’· d r 4 eo ’·P d 3 r’ r intégrale de volume intégrale de surface 1 V( r ) = 4 eo P·d. S 1 - r 4 eo ’·P d 3 r’ r Or on a déjà vu que le potentiel est de la forme V(r) = (1/ 4 eo ) dq/r Donc si N est le vecteur normal à la surface: P·N représente une densité de charge surfacique de charges liées, tandis que - ’·P représente une densité de charge volumique. Si la polarisation est constante dans l’espace, alors seule la densité de charge surfacique existe. Un diélectrique parallèlépipédique où la polarisation serait perpendiculaire à deux faces se comporte comme un condensateur plan ! Electromagnétisme - L 2 PCGI - Université Rennes 1 - 2005 55

3. 9 Cas des milieux isolants (diélectriques) La conservation de charge, implique si la distribution de charge volumique (de charges liées) est non nulle, il existe un courant de polarisation associé: rliée ·P ·jpol = - = jpol = P t t t Lorsqu’on applique l’équation de Poisson reliant champ électrique et charge, il faut prendre la charge totale, c’est à dire la somme des charges libres et liées. On introduit alors une nouvelle grandeur, appelée Déplacement Electrique l’on note D et qui est définie par: D = eo. E + P ·D = rlibres On peut également dire qu’à l’intérieur d’un diélectrique le champ électrique est la somme de deux contributions: une contribution associées aux charges libres D/eo et une contribution associée aux charges liées -P/eo. Electromagnétisme - L 2 PCGI - Université Rennes 1 - 2005 56

3. 9 Cas des milieux isolants (diélectriques) Sans rentrer dans le détail de l’origine microscopique des dipôles, on peut traiter la polarisation électrique d’un diélectrique dans le cadre de la Réponse Linéaire, c’est à dire qu’on écrit que la réponse « Polarisation » est proportionnelle à l’excitation « champ électrique » : P = E D = eo(1+ )E = eoer E = e E est la susceptibilité électrique er est la permittivité électrique relative du milieu e est la permittivité électrique ou constante diélectrique du matériau Dans le vide =0 et er =1. La plupart des matériaux ont une permittivité relative comprise entre 2 et 5. Cependant on peut trouver des matériaux où cette permittivité relative peut dépasser 105 ! Electromagnétisme - L 2 PCGI - Université Rennes 1 - 2005 57

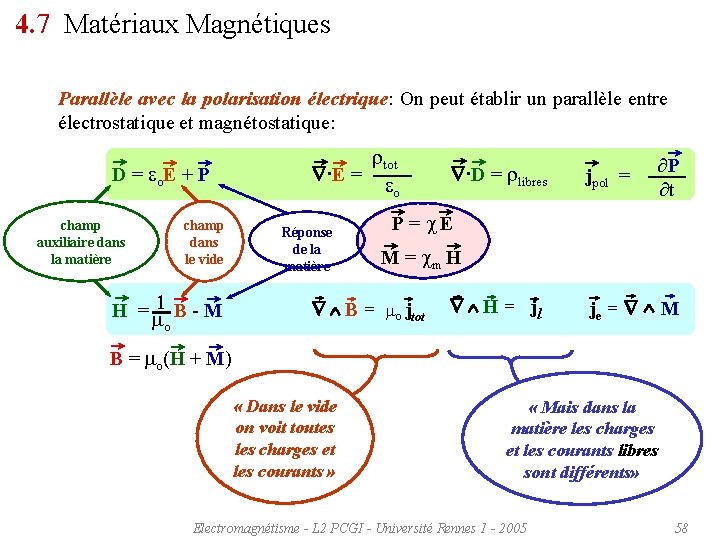
4. 7 Matériaux Magnétiques Parallèle avec la polarisation électrique: On peut établir un parallèle entre électrostatique et magnétostatique: D = eo. E + P champ auxiliaire dans la matière champ dans le vide 1 H = B - M mo rtot ·E = eo Réponse de la matière ·D = rlibres jpol = P t P = E M = m H B = mo jtot H = jl je = M B = mo(H + M) « Dans le vide on voit toutes les charges et les courants » « Mais dans la matière les charges et les courants libres sont différents» Electromagnétisme - L 2 PCGI - Université Rennes 1 - 2005 58