Universit de Rennes 1 Licence Sciences Technologie Sant

Université de Rennes 1 Licence Sciences Technologie Santé L 2 -PCGI Electromagnétisme Philippe Rabiller 2005 Electromagnétisme - L 2 PCGI - Université Rennes 1 - 2005 1

Bibliographie • BERKLEY - Cours de Physique - 2. électricité et magnétisme, E. M. Purcell (éditions Dunod 1998). • Champs et ondes électromagnétiques, P. Lorrain et D. R. Corson (éditions Armand Colin_collection U 1979). • Comprendre et Appliquer l’électrostatique, J. P. Longchamp (éditions MASSON 1991) • Comprendre et Appliquer l’électromagnétisme, J. P. Longchamp (éditions MASSON 1990) • Le cours de physique de Feynman: mécanique 1 & 2 (éditions DUNOD 1999) • . . . • Electromagnétisme - L 2 PCGI - Université Rennes 1 - 2005 2

Plan du cours • ch. 1 Introduction • ch. 2 Vecteurs et champs • ch. 3 Champ et Potentiel électrostatiques • intro au ch. 4: relativité restreinte • ch. 4 Champ Magnétique • ch. 5 Induction électromagnétique • ch. 6 Propagation des ondes électromagnétiques • ch. 7 Rayonnement électromagnétique Electromagnétisme - L 2 PCGI - Université Rennes 1 - 2005 3

Chapitre 3: Champ et Potentiel électrostatiques 3. 1 Additivité de la loi de Coulomb 3. 2 Energie électrostatique d’un système de charges 3. 3 Champ Electrique 3. 4 Potentiel Electrostatique 3. 5 Théorème de Gauss / Equation de Lapalce 3. 6 Distributions de charges / symétrie 3. 7 Dipôle électrique 3. 8 Densité d’énergie dans un champ électrique 3. 9 Cas des conducteurs parfaits 3. 10 Cas des milieux isolants (diélectriques) Electromagnétisme - L 2 PCGI - Université Rennes 1 - 2005 4

3. 1 Additivité de la loi de Coulomb La force exercée sur une charge q 1 par deux autres charges q 2 et q 3 est la somme (vectorielle!) des forces exercées respectivement par q 2 sur q 1 et q 3 sur q 1: q 3 F 31 F 21 F 1 = 1 r 31 q 1 q 2 4 peo r 21 2 q 2 r 21 u 21 + 1 q 1 q 3 4 peo r 31 2 u 31 Plus généralement la force exercée sur une charge test q par un ensemble de charges {Qi} est la somme vectorielle des forces exercées respectivement par toutes les charges Qi prises individuellement sur la charge test q: i Fq = FQiq = i 1 Qiq 4 peo r. Qiq 2 u. Qiq Electromagnétisme - L 2 PCGI - Université Rennes 1 - 2005 5

3. 2 Energie électrostatique d’un système de charges Soit une charge test q. Calculons le travail fourni pour amener cette charge depuis l’infini jusqu’à une distance r d’une autre charge Q fixe: Q dr u q r FQq q. Q d. W = F·dr = u·dr = - |dr| 4 peo r 2 r r q. Q Qq 1 r -1 W r = d. W = F ·dr = 2 dr = [ ] r 4 peo r o q. Q Wélectrostatique = 4 peor Rapprocher deux charges de même signe coûte de l’énergie, tandis que rapprocher deux charges de signe opposés fournit de l’énergie. Si les deux charges restent à une distance fixe l’une de l’autre c’est qu’une autre force empêche les charges de s’éloigner si q et Q ont même signe, ou de se rapprocher si q et Q sont de signes opposés. Nous ne cherchons pas à préciser la nature de cette force ce cours. Electromagnétisme - L 2 PCGI - Université Rennes 1 - 2005 6

3. 2 Energie électrostatique d’un système de charges Q dr u q r FQq u’ q F’ dr’ q. Q d. W = F’·dr’ = u’·dr’ = - |dr’|cos(q) = - |dr’’| 4 peo r 2 Quand |r ’| passe de à r, alors r’’ passe également de à r. Le travail fourni pour faire passer une charge test q d’une distance à une distance r d’une autre charge source Q ne dépend pas du chemin suivi, mais uniquement de la distance !!! On parle alors de force centrale Electromagnétisme - L 2 PCGI - Université Rennes 1 - 2005 7

3. 2 Energie électrostatique d’un système de charges Si on considère à présent un système de trois charges q 1, q 2 et q 3, alors il faut ajouter à l’énergie électrostatique du système de charge {q 1, q 2} l’énergie correspondant au travail amenant la charge q 3 en présence des deux autres: q 2 q 1 q 2 W{1, 2} = 4 peor 12 r 32 q 1 q 3 r 31 d. W 3= F 3·dr = F 13·dr + F 23·dr = d. W{1, 3} + d. W{2, 3} q 1 q 2 q 1 q 3 q 2 q 3 W{1, 2, 3} = + 4 peor 12 4 peor 13 4 peor 23 Pour un système de N charges: {qi}, i=1, N qiqj 1 WN = = 2 i, j i 4 peorij i, j>i Electromagnétisme - L 2 PCGI - Université Rennes 1 - 2005 qiqj 4 peorij 8

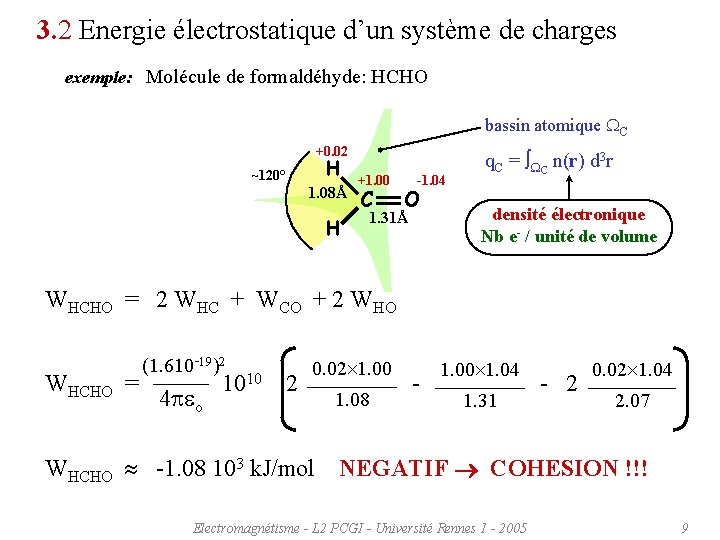
3. 2 Energie électrostatique d’un système de charges exemple: Molécule de formaldéhyde: HCHO bassin atomique WC +0. 02 ~120° H 1. 08Å H +1. 00 C -1. 04 O 1. 31Å q. C = WC n(r) d 3 r densité électronique Nb e- / unité de volume WHCHO = 2 WHC + WCO + 2 WHO WHCHO (1. 610 -19)2 0. 02 1. 00 4 peo 1. 08 1. 00 1. 04 = 1010 2 - 2 1. 31 0. 02 1. 04 2. 07 WHCHO -1. 08 103 k. J/mol NEGATIF COHESION !!! Electromagnétisme - L 2 PCGI - Université Rennes 1 - 2005 9

3. 3 Champ Electrique Reprenons le cas d’un ensemble de charges {Qi} agissant sur une charge « test » q à la position r. 1 Qiq i Fq (r) = FQiq = i 4 peo r. Qiq 2 u. Qiq La force est proportionnelle à la charge test q : u = q E( r ) r i 4 pe Fq ( r ) = q Champ Electrique Qi 1 o Qiq E ( r ) = 2 i Qiq 1 Qi 4 peo r. Qiq 2 u. Qiq • Les charges Qi sont la source du champ électrique. • Le champ électrique est une propriété locale. Il suffit de connaître le champ électrique en tout point de l’espace pour savoir quelle est la force agissant sur une charge test en ce point ! Electromagnétisme - L 2 PCGI - Université Rennes 1 - 2005 10

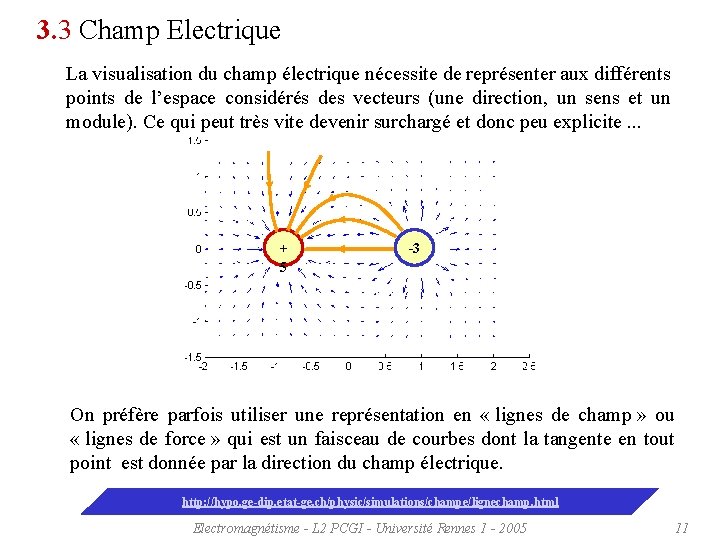
3. 3 Champ Electrique La visualisation du champ électrique nécessite de représenter aux différents points de l’espace considérés des vecteurs (une direction, un sens et un module). Ce qui peut très vite devenir surchargé et donc peu explicite. . . + 5 -3 On préfère parfois utiliser une représentation en « lignes de champ » ou « lignes de force » qui est un faisceau de courbes dont la tangente en tout point est donnée par la direction du champ électrique. http: //hypo. ge-dip. etat-ge. ch/physic/simulations/champe/lignechamp. html Electromagnétisme - L 2 PCGI - Université Rennes 1 - 2005 11

3. 4 Potentiel Electrique Différence de potentiel: Nous avons vu que le travail de la force électrique exercée sur une charge par un ensemble d’autres charges est indépendant du chemin suivi. Nous pouvons reprendre ce développement en introduisant le champ électrique et ainsi écrire: r 2 r W 12 = Fq·dr = q E( r ) ·dr 1 1 r 2 r V 21 = - E( r ) ·dr 1 V 21 est une grandeur scalaire, encore appelée différence de potentiel, qui représente le travail par unité de charge nécessaire pour amener une charge positive , dans le champ le E, de la position r 1 à la position r 2. Dans le système international elle est mesurée en Volts (V). La dimension du champ électrique est donc V. m-1. Electromagnétisme - L 2 PCGI - Université Rennes 1 - 2005 12

3. 4 Potentiel Electrique Fonction potentiel électrostatique: Nous pouvons écrire la différence de potentiel V 21 comme la différence des valeurs prises par une fonction scalaire V(r) aux positions r 1 et r 2 r - (V 2 - V 1) = E( r ) ·dr 1 En différenciant (dérivant) chaque membre de l’équation ci-dessus, nous pouvons alors écrire (cf. chapitre 2) : V( r + dr ) = V( r ) + V • dr Par identification nous voyons donc que le champ électrique (vectoriel) dérive d’un potentiel (champ scalaire) : - V( r ) = E( r ) Electromagnétisme - L 2 PCGI - Université Rennes 1 - 2005 13

3. 4 Potentiel Electrique Surfaces équipotentielles / lignes de champ: puisque le champ électrique dérive d’un potentiel, c’est à dire que le champ est donné par le gradient d’une fonction scalaire, alors le champ électrique E( r ) est perpendiculaire à la surface V ( r )=cste encore appelée surface équipotentielle. + 5 -3 Le potentiel électrostatique est défini à une constante près! En effet, le gradient de V( r ) ne change pas si on lui ajoute une constante. En général, on prend V( r ) = 0 à l’infini (par rapport à toute charge). Electromagnétisme - L 2 PCGI - Université Rennes 1 - 2005 14

3. 5 Théorème de Gauss / Equation de Laplace approche intégrale - théorème de Gauss: Le flux du champ électrique à travers une surface fermée est égal à la charge totale, comprise à l’intérieur de la surface, divisée par la permittivité du vide eo. exemple: Prenons une charge ponctuelle q située au centre d’une sphère de rayon R. En tout point de la surface de la sphère, le champ électrique est perpendiculaire à la surface (dirigé suivant le rayon). Son module est constant et vaut q/4 peo. R 2. Pour calculer le flux , nous utilisons les coordonnées sphériques. Un élément de surface d. S vaut R 2 sin(q)dqd. L’élément de flux E·d. S ne dépend donc plus de R et l’intégration sur toute la surface conduit donc à: = E·d. S = p 2 p 0 0 4 pe q sin(q)dqd = o Electromagnétisme - L 2 PCGI - Université Rennes 1 - 2005 q eo 15

3. 5 Théorème de Gauss / Equation de Laplace Comment généraliser au cas d’une distribution de charges ponctuelles ? d. S w q 2 r q 1 ds d s = E(r)ds d S = E(R) d. S cos(w) R d. W = d. S cos(w) /R 2 = sin(q)dqd = ds/r 2 q q ds ds R 2 d S = E(R) d. S cos(w) = = E(r) ds = d s 2 2 2 4 peo R r 4 peo r Pour la charge q 1, le flux est le même à travers les deux surfaces !!! Electromagnétisme - L 2 PCGI - Université Rennes 1 - 2005 16

3. 5 Théorème de Gauss / Equation de Laplace Comment généraliser au cas d’une distribution de charges ponctuelles ? d. S q 2 Pour la charge q 2, nous pouvons faire le même raisonnement à partir d’une deuxième sphère à l’intérieur de la surface et centrée sur q 2. q 1 Le champ électrique étant additif comme la force de Coulomb, nous pouvons écrire le flux total dû aux charges q 1 et q 2 comme la somme des flux « partiels » individuels 1 et 2 . Ceux là même se déduisant du flux à travers des sphères centrées sur les charges, on en déduit donc la généralisation du théorème de Gauss: qi = E·d. S = = eo Qtotal eo Electromagnétisme - L 2 PCGI - Université Rennes 1 - 2005 17

3. 5 Théorème de Gauss / Equation de Laplace approche locale - équation de Poisson: Le théorème de la divergence (cf. chapitre 2) peut s’appliquer au cas du champ électrique: Qtotal 3 • = d = d S E d. S V • E r = eo S Si le nombre de charges par unité de volume est grand dans le volume considéré, alors on peut passer à la limite et définir une densité locale de charge r: dq ( r ) 3 r r( r ) = Q = r( r ) d total 3 dr L’égalité des intégrales doit être vraie, quelque soit la forme de la surface et du volume délimité. Ceci implique donc que l’égalité est vérifiée si les intégrands sont toujours égaux. Ceci donne l’équation de Poisson qui est une version locale du théorème de Gauss: Poisson r · E( r ) = = - 2 V( r ) eo Electromagnétisme - L 2 PCGI - Université Rennes 1 - 2005 Laplace 18

3. 6 Distribution de charges / Symétrie • Dans la nature, nous n’avons que très rarement affaire à un système de « quelques » charges ponctuelles, mais plus souvent à des systèmes contenant un très grand nombre de charges. • Calculer « analytiquement » la force de Coulomb, le champ électrique ou le potentiel électrostatique devient chose peu évidente. On préfère alors utiliser une représentation continue de la charge en introduisant la notion de densité de charge et utiliser les propriétés de symétrie des systèmes (invariances) pour simplifier au maximum les calculs. • Néanmoins, pour essayer de visualiser les choses simplement et limiter le nombre de paramètres pertinents servant à décrire un système, on cherche souvent un système équivalent de charges ponctuelles approchant aux mieux le champ électrique ou le potentiel électrostatique. Electromagnétisme - L 2 PCGI - Université Rennes 1 - 2005 19

3. 6 Distribution de charges / Symétrie Densité de charge: • Appliquons le théorème de Gauss, pour une surface sphérique, à un petit système borné, à distribution uniforme et sphérique de charge : • Par symétrie, on montre qu’en tout point à l ’extérieur de la surface, le champ électrique est radial, c’est à dire que son module est constant quels que soient les angles polaires q et . • Le théorème de Gauss donne 4 pr 2 E(r) = Qtot/eo ou de façon équivalente, E(r) = Qtot/4 pr 2 eo. Tout se passe donc comme si toutes les charges étaient concentrées en une seule charge ponctuelle Qtot au centre de la sphère ! • On peut donc considérer tout volume « infinitésimal » d 3 r contenant une charge dq, comme une charge ponctuelle centrée à la position r. On appelle densité de charge volumique r le quotient r = dq/ d 3 r. Electromagnétisme - L 2 PCGI - Université Rennes 1 - 2005 20

3. 6 Distribution de charges / Symétrie Distribution surfacique de charge: • Soit un système chargé avec une densité volumique de charge r. Supposons que ce système présente une dimension d’épaisseur faible par rapport aux deux autres dimensions (plaque, disque, couche sphérique, etc. ). r d s • Alors dans la direction correspondant à l’épaisseur dz=d, on peut considérer que la densité ne varie pas, de sorte qu’il est suffisant de repérer un élément de surface d. S = dxdy ou rdrdq par ses coordonnées (x, y) ou (r, q) pour connaître le nombre de charge dans cet élément: dn = r d 3 r = r dxdydz = rd dxdy = s d. S • La quantité s s’appelle la densité surfacique de charge: Electromagnétisme - L 2 PCGI - Université Rennes 1 - 2005 21

3. 6 Distribution de charges / Symétrie Distribution linéique de charge: • De même pour un objet dont la section dans deux dimensions est très petite devant la troisième dimension, on peut se ramener à une distribution linéique de charge l. r l = r A A Electromagnétisme - L 2 PCGI - Université Rennes 1 - 2005 22

3. 6 Distribution de charges / Symétrie Utilisation de la symétrie et du théorème de Gauss pour calculer le champ électrique. • Lorsqu’un système possède une certaine symétrie (sphérique, axiale, cubique, hexagonale, etc. ) ses propriétés doivent refléter cette symétrie (Pierre Curie). Il est alors assez facile de calculer le champ électrique à l’aide du théorème de Gauss en choisissant une surface « de Gauss » adaptée à la symétrie. • Distribution sphérique: 1 r(r)r 2 sin(q)dqd dr (R) = 4 p. R 2 E(R) = eo ~ Q(R) E(R) = eo. R 2 ~ R Q(R) = r(r)r 2 dr 0 Fonction de distribution radiale Electromagnétisme - L 2 PCGI - Université Rennes 1 - 2005 23

3. 6 Distribution de charges / Symétrie • Distribution sphérique: – homogène r(r) = r =cste si r < Ro: R < Ro R > Ro ~ R Q(R) = r r 2 dr = r R 3/3 0 ~ Ro Q(R) = r r 2 dr = r Ro 3/3 0 r E(R) = r R 3 eo r. Ro 3 eo Ro R 2 E(R) ~1/R 2 Ro Ro Electromagnétisme - L 2 PCGI - Université Rennes 1 - 2005 24

3. 6 Distribution de charges / Symétrie On peut retrouver le même résultat à partir de l’équation locale: ·E=r/eo En coordonnées sphériques seule la composante radiale de la divergence du champ électrique (qui a la symétrie sphérique) est non nulle : E(r) r(r) 2 E(r) + = r r eo R < Ro r(r)=r On cherche E(R) de la forme b Ra b(2+a)Ra-1 = r/eo Pour que se soit vrai R il faut a=1 et donc b = r/3 eo On retrouve E(R) = r. R/3 eo R > Ro r(r)=0 On doit alors avoir b(2+a) Ra-1 = 0 a=-2 Comme E(Ro) = r. Ro/3 eo alors b = r. Ro 3/3 eo On retrouve E(R) = r. Ro 3/3 R 2 eo Electromagnétisme - L 2 PCGI - Université Rennes 1 - 2005 25

3. 6 Distribution de charges / Symétrie pour le calcul du potentiel, nous utilisons le fait que V aussi doit avoir la symétrie sphérique: E = - V( r ) E(r) = - V(r)/ r. R < Ro E(R) ~ (r/3 eo) R V(R) = - (r/3 eo) R 2/2 +V(0) R > Ro E(R) ~ (r. Ro 3/3 eo) / R 2 V(R) = (r. Ro 3/3 eo) / R + cste’ R V( ) = 0 cste’ = 0 V(Ro) = r. Ro 2/3 eo ~ -R 2 V(0) = r. Ro 2/2 eo ~1/R Electromagnétisme - L 2 PCGI - Université Rennes 1 - 2005 26

3. 6 Distribution de charges / Symétrie • Distribution sphérique: – linéaire r(r) = a r si r < Ro R > Ro ~ R Q(R) = a 0 ~ r 3 dr = a R 4/4 Ro Q(R) = a r 3 dr = a Ro 4/4 0 r a R 2 E(R) = 4 eo E(R) = a. Ro 4 eo 2 Ro R 2 E Ro Ro Electromagnétisme - L 2 PCGI - Université Rennes 1 - 2005 27

3. 6 Distribution de charges / Symétrie • Distribution sphérique: – couche homogène r(r) = r si Ro< r < Ro+d ~ R < Ro E(R) = 0 Q(R) = 0 ~ Ro+d Q(R) = r r 2 dr rd. Ro 2 R > Ro+d Ro Ro < R=Ro+u < Ro+d r ~ Ro+u Q(R) = r r 2 dr ru. Ro 2 Ro rd E(R) eo E(R) 2 Ro R ru eo E Ro Ro Si d tend vers zéro: saut de champ électrique !!! Electromagnétisme - L 2 PCGI - Université Rennes 1 - 2005 28

3. 6 Distribution de charges / Symétrie • Distribution plane: – plan homogène infini de densité de charge surfacique s • Tout axe perpendiculaire au plan infini est un axe de symétrie axiale, donc le champ électrique est perpendiculaire au plan. Sl E Sa • Il suffit de prendre une surface adaptée à cette symétrie, i. e. un cylindre au plan • Pour les faces latérales, le flux vaut 2 E(r)Sl. • Pour la face axiale, le flux est nul (E Sa). r • La charge totale vaut s. Sl • Le champ électrique vaut donc E(r) = s/2 eo Le champ électrique créé par un plan infini est indépendant de la distance au plan ! Electromagnétisme - L 2 PCGI - Université Rennes 1 - 2005 29

3. 6 Distribution de charges / Symétrie • Distribution plane: – disque homogène • Dans ce cas seul le calcul du champ le long de l’axe de révolution du disque est aisé. R srdqdr 1 d. Ez = cos(w) 4 peo r 2 +z 2 s q d. Ez r z d. E w rdr sz d. Ez = dq 4 peo (r 2 +z 2)3/2 R Ez = sz rdr 2 eo 0 (r 2 +z 2)3/2 s z Ez = 1 2 eo |z| 1 1 +R 2/z 2 Ici on a cherché une fonction f=gn et g=ra+c a=2 et n=-1/2 f’ = n g’ gn-1 r / (r 2+c ) 3/2 Electromagnétisme - L 2 PCGI - Université Rennes 1 - 2005 30

3. 6 Distribution de charges / Symétrie • Distribution plane: s z Ez = 1 2 eo |z| – disque homogène 1 1 +R 2/z 2 R s • Lorsque R tend vers l’infini ou z tend vers zéro, on retrouve le résultat du plan infini obtenu par le théorème de Gauss: E=s/2 eo. Ez E z Electromagnétisme - L 2 PCGI - Université Rennes 1 - 2005 31

3. 6 Distribution de charges / Symétrie approche intégrale du théorème de Gauss pour le potentiel: Pour une charge ponctuelle q, la symétrie est sphérique et on peut utiliser le gradient en coordonnées sphériques pour obtenir: E(r) = - V(r)/ r Comme pour une charge ponctuelle on a E(r) = q / (4 peor 2) On obtient donc pour le potentiel V(r) avec la référence V( )=0: V(r) = q 4 peor ! ici « r » représente la distance entre le point où on calcule le potentiel et la charge source Si on a deux charges q 1 et q 2, pour calculer le potentiel en ro on utilise le fait que le champ électrique (comme la force) est une grandeur additive et donc le potentiel électrostatique est aussi additif : q 1 q 2 V( ro) = + 4 peor 1 o 4 peor 2 o Electromagnétisme - L 2 PCGI - Université Rennes 1 - 2005 32

3. 6 Distribution de charges / Symétrie approche intégrale du théorème de Gauss pour le potentiel: Pour une distribution quelconque de charge on peut généraliser l’expression pour aboutir à : 1 V( r ) = 4 peo ! r( r ’)d 3 r’ | r - r ’| ici r représente la position où on calcule le potentiel (position d’une charge test) et r ’ couvre tout l’espace où la densité de charge (source) est non nulle On peut donc calculer le potentiel électrostatique par cette formule et calculer ensuite le champ électrique lorsque c’est préférable d’un point de vue calcul. . . Electromagnétisme - L 2 PCGI - Université Rennes 1 - 2005 33

3. 7 Dipôle électrique Lorsque les distributions de charge sont compliquées, on essaie parfois de trouver un modèle équivalent, simple, constitué de quelques charges à partir desquelles on pourra établir des raisonnements ou calculs analytiquement. Parmi les modèles plus simples, ceux du dipôle et quadrupôle sont les plus employés (interaction rayonnement/matière, phénomènes de résonance électrique ou magnétique, etc. ). Repartons de l’expression générale du potentiel électrostatique: 1 V( r ) = 4 peo r( r ’)d 3 r’ | r - r ’| et plaçons nous dans le cas d’une distribution quelconque de charge: r’ | r - r’ | = R r Electromagnétisme - L 2 PCGI - Université Rennes 1 - 2005 34

3. 7 Dipôle électrique R = [ r 2 + r'2 - 2 rr' cos(q) ]1/2 | r - r’ | = R r’ q r Ce qui nous intéresse en général, c’est le calcul du potentiel LOIN de la distribution de charge. On peut donc faire un développement limité en puissances de r’/r puisque dans ce cas r’ << r, R: (1+d)-1/2 1 - 1/2 d + 3/8 d 2 +. . . Dans l’expression du potentiel, r (ou rn) est une constante qui peut être sortie de l’intégrale: Electromagnétisme - L 2 PCGI - Université Rennes 1 - 2005 35

3. 7 Dipôle électrique On a donc un développement du potentiel électrostatique en puissances de la distance du point « test » à un point référence de la distribution de charge: 1 V( r ) = 4 peo r( r ’)d 3 r’ 4 pe | r - r ’| Mo 1 o M 1 M 2 + + . . . r r 2 r 3 Les quantités Mo, M 1, M 2 , M 3 , M 4 etc. s’appellent les moments multipolaires de la distribution de charge : monopôle, dipôle, quadrupôle, octupôle, hexadecapôle, etc. Le terme correspondant au monopole correspond à l’expression pour une charge ponctuelle ou pour une distribution à symétrie sphérique. Le deuxième terme (dipôle) est équivalent à un système de deux charges opposées. Il est nul pour toute distribution de charge possédant un centre de symétrie d’inversion Electromagnétisme - L 2 PCGI - Université Rennes 1 - 2005 36

3. 7 Dipôle électrique Dipôle: intéressons nous plus en détail au moment dipolaire. Le terme r’cos(q) peut aussi s’écrire comme le produit scalaire du vecteur r’ avec un vecteur normé parallèle au vecteur r. Le potentiel électrostatique « dipolaire » s’écrit alors: | r - r’ | = R r’ q r Soit en introduisant le vecteur dipôle électrique : (px = xrd 3 r’ ; py = yrd 3 r’ ; pz = zrd 3 r’ ) Electromagnétisme - L 2 PCGI - Université Rennes 1 - 2005 37

3. 7 Dipôle électrique Plaçons l’origine au « centre de charge » de la distribution (barycentre) et calculons le potentiel pour un dipôle pointant suivant la direction « z » d’un système cartésien. Alors en coordonnées polaires cos(q) = z / [r 2+z 2]1/2. q z r Le potentiel ne dépend pas de , car la symétrie est axiale. On en déduit alors les composantes du champ électrique dont l’intensité décroît en 1/r 3: Electromagnétisme - L 2 PCGI - Université Rennes 1 - 2005 38

3. 7 Dipôle électrique Montrons à présent que l’on retrouve le même résultat pour un système de deux charges ponctuelles opposées Q et -Q séparées d’une distance a. Q a/2 -Q r+ q r r- 1 1 1 V( r ) = 4 peo r+ r- En effectuant le même genre de développement limité au 1 er ordre en r+/r et r-/r on obtient: V( r ) = Soit en introduisant le vecteur dipôle p = Qa uz : Qa cos(q) 4 peor 2 Vp( r ) = Electromagnétisme - L 2 PCGI - Université Rennes 1 - 2005 p·r 4 peor 3 39

3. 7 Dipôle électrique Force agissant sur un dipôle: Si un dipôle est plongé dans un champ électrique uniforme, la force s'appliquant sur une des charge est exactement l’opposé de la force agissant sur la deuxième charge. Dans ce cas la force totale est nulle et seul un couple peut s’exercer si la force et le rayon d’application de la force sont non colinéaires (G = r F). Q q E F+ +QE -a/2 uz -QE - = +a/2 uz -a/2 uz F- = +a/2 uz = + - = p E -Q | G | = | p | | E | sin(q) est minimum quand q = 0 alignement ! p 0 Energie pour renverser un dipôle: W = Gdq = 2 p. E Electromagnétisme - L 2 PCGI - Université Rennes 1 - 2005 40

3. 7 Dipôle électrique Force dans un champ inhomogène: Si le champ n’est pas homogène, les deux charges ne voient pas le même champ localement, le bilan des force n’est pas nul et le dipôle peut être mis en mouvement (antennes, émetteurs). F+ = +Q E + d. E/2 Q Chacune des composantes de la force peut être calculée à l’aide du gradient de champ: d. Ex = Ex·dx auz· Ex = (1/Q) p · Ex -Q Fx = p · Ex F- = -Q E - d. E/2 Fy = p · Ey Fz = p · Ez Electromagnétisme - L 2 PCGI - Université Rennes 1 - 2005 41

3. 8 Densité d’énergie dans un champ électrique Prenons le cas d’une sphère de rayon R et chargée en surface avec une densité de charge s. Le théorème de Gauss pour le champ à la surface donne: 4 p. R 2 E = Q/eo = 4 p. R 2 s/eo E = s/eo Tandis qu’à l ’intérieur de la sphère, le champ est nul puisque la charge est nulle. Si on considère que la charge de surface est une charge volumique r répartie sur une fine épaisseur d. R telle s=r d. R, alors la force moyenne exercée sur un petit élément de surface est simplement: d. Fmoy = 1/2 (d. Fint + d. Fext)= 1/2 sd. S (0 + s/eo) (F=q. E) C’est à dire que le force moyenne exercée sur toute la sphère est: Fmoy = 4 p R 2 (1/2 eo) s 2 d. S = 2 p R 2 s 2 /eo Cette force tend à dilater la sphère. Si tel était le cas, avec un accroissement de rayon d. R, alors le travail fourni serait: d. W = (2 p R 2 s 2/eo) d. R Electromagnétisme - L 2 PCGI - Université Rennes 1 - 2005 42

3. 8 Densité d’énergie dans un champ électrique C’est à dire que le fait de maintenir les charges uniformément réparties sur la fine couche d’épaisseur d. R - au seul endroit où le champ électrique est non nul - coûte une énergie: 4 ps 2 R 2 eo 2 d 3 r d. W = d. R = E 2 2 eo Cela revient pour calculer l’énergie potentielle d’une distribution de charge à attribuer à chaque région, où il règne un champ électrique non nul, une densité locale d’énergie: eo eo 2 d. U( r ) = = E( r )·E( r ) = | V( r ) | 3 2 2 dr d. W On peut également donner une expression intégrale: qiqj 1 WN = 2 i, j i 4 peorij 1 1 = q V 2 i, j i i i 2 Electromagnétisme - L 2 PCGI - Université Rennes 1 - 2005 r( r ) V( r )d 3 r 43

3. 8 Cas des conducteurs parfaits Champ électrique dans un conducteur parfait: Dans un conducteur supposé parfait (homogène et isotrope), des charges sont libres de se mouvoir sous l’action d’un champ extérieur, mais en tout point du milieu conducteur, ces charges sont compensées - sauf peut-être en surface ainsi qu’à l’échelle atomique ou sub-atomique - par d’autres charges fixes ou libres elles aussi. Il s’en suit qu’en tout point du conducteur la densité de charge (moyenne locale) est nulle et donc le champ électrique est nul aussi. Le potentiel électrostatique est constant dans le conducteur. A l’extérieur, le champ électrique n’est pas forcément nul et la surface du conducteur est une surface équipotentielle pour ce champ électrique (E S). Le théorème de Gauss indique alors qu’il doit exister une charge de surface: 0 + End. S = sd. S/eo s = En eo Ei=0 En ainsi qu’une charge totale: Q = sd. S = eo En·d. S S Electromagnétisme - L 2 PCGI - Université Rennes 1 - 2005 S 44

3. 9 Cas des conducteurs parfaits Il faut bien noter ici que la charge de surface s n’est pas la cause du champ électrique. Le champ est dû à l’ensemble de toutes les charges et la charge à la surface du conducteur se réajuste de sorte à annuler le champ électrique à l’intérieur du conducteur. Le problème consistant à calculer les charges accumulées à la surface de conducteurs plongés dans un champ électrique (ou soumis à un potentiel donné) n’est une chose aisée que dans le cas de systèmes à un ou deux conducteurs à géométrie simple. Electromagnétisme - L 2 PCGI - Université Rennes 1 - 2005 45

3. 9 Cas des conducteurs parfaits Charge d’une sphère conductrice de rayon R portée à un potentiel Vo: Le potentiel électrostatique étant constant à l’intérieur de la sphère conductrice, il suffit de savoir calculer le potentiel au centre. La charge étant concentrée en surface, un élément de charge volumique rd 3 r’ vaut s. R 2 sin(q)dqdj pour r’=R et zéro ailleurs. La charge totale vaut Q=4 p. R 2 s. Le potentiel électrostatique peut être calculé par la formule générale en r=0: 1 V( r ) = 4 peo r( r ’)d 3 r’ | r - r ’| s. R Q V(r<R) = V(0) = Vo = = 4 peo. R eo On retrouve naturellement l’expression qu’on aurait obtenu avec le théorème de Gauss pour le champ électrique à la surface de la sphère puis en intégrant en coordonnées sphérique pour obtenir le potentiel. La densité de charge surfacique est constante (symétrie sphérique). Q = 4 peo. RVo s = eo. Vo/R Electromagnétisme - L 2 PCGI - Université Rennes 1 - 2005 46

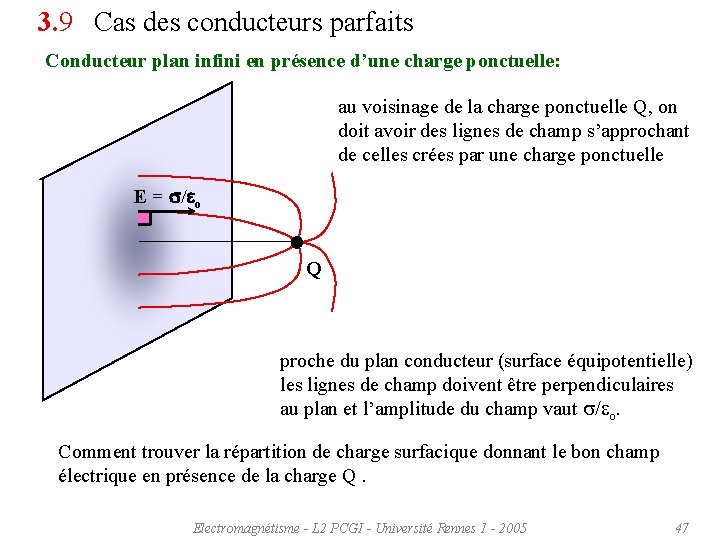
3. 9 Cas des conducteurs parfaits Conducteur plan infini en présence d’une charge ponctuelle: au voisinage de la charge ponctuelle Q, on doit avoir des lignes de champ s’approchant de celles crées par une charge ponctuelle E = s/eo Q proche du plan conducteur (surface équipotentielle) les lignes de champ doivent être perpendiculaires au plan et l’amplitude du champ vaut s/eo. Comment trouver la répartition de charge surfacique donnant le bon champ électrique en présence de la charge Q. Electromagnétisme - L 2 PCGI - Université Rennes 1 - 2005 47

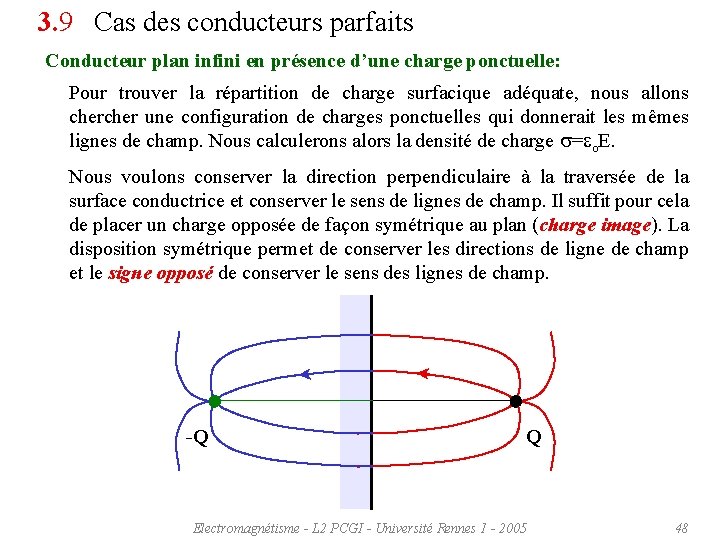
3. 9 Cas des conducteurs parfaits Conducteur plan infini en présence d’une charge ponctuelle: Pour trouver la répartition de charge surfacique adéquate, nous allons cher une configuration de charges ponctuelles qui donnerait les mêmes lignes de champ. Nous calculerons alors la densité de charge s=eo. E. Nous voulons conserver la direction perpendiculaire à la traversée de la surface conductrice et conserver le sens de lignes de champ. Il suffit pour cela de placer un charge opposée de façon symétrique au plan (charge image). La disposition symétrique permet de conserver les directions de ligne de champ et le signe opposé de conserver le sens des lignes de champ. -Q Q Electromagnétisme - L 2 PCGI - Université Rennes 1 - 2005 48

3. 9 Cas des conducteurs parfaits Conducteur plan infini en présence d’une charge ponctuelle: Calculons le champ en coordonnées cylindriques. Compte tenu de la symétrie axiale, le champ ne dépend que du rayon r et de la distance au plan z. -2 Q Ez(r) = cos(q) 4 peo(r 2+z 2) r Ez(r) = z -Q -Qz 2 peo(r 2+z 2)3/2 Q s(r) = eo. Ez(r) = -Qz 2 p (r 2+z 2)3/2 On peut vérifier que la charge totale de surface ainsi obtenue donne bien par intégration la charge « image » -Q. zrdr -1 s 2 prdr = -Q = -Q 2 2 3/2 (1+u 2)1/2 0 0 (r +z ) 0 Electromagnétisme - L 2 PCGI - Université Rennes 1 - 2005 49

3. 9 Cas des conducteurs parfaits Condensateur plan / capacité Intéressons nous maintenant au cas de deux plaques parallèles séparées par une distance e très inférieure aux dimensions des plaques. Les plaques sont portées aux potentiels V 1 et V 2. Le champ est donc perpendiculaire aux plans et si l’une des plaques porte une charge +Q, +Q l’autre porte forcément une charge -Q (cf. charge image). V 1 e V 2 -Q La distance entre plaques étant très inférieure aux dimensions des plaques, nous pouvons considérer le système comme deux plans parallèles infinis. Le champ est donc nul à l’extérieur des plaques et constant et uniforme à l’intérieur E=s/eo =(V 1 -V 2)/e (seulement aux extrémités des lignes de champ non uniformes existent à l’intérieur comme à l’extérieur). Si S est la surface des plaques, la charge Q s’écrit Q = s. S = C (V 1 -V 2) eo. S La quantité C = s’appelle la capacité du condensateur. e Elle se mesure en farads. On utilise souvent des unités plus petites (µF, p. F). Electromagnétisme - L 2 PCGI - Université Rennes 1 - 2005 50

3. 9 Cas des conducteurs parfaits Condensateur plan / capacité L’énergie électrostatique W emmagasinée dans un condensateur est le produit de la densité d’énergie électrostatique eo. E 2/2 multipliée par le volume Se. En introduisant la capacité C et la différence de potentiel V 1 -V 2 = V 12 cela conduit à : 1 2 W = C V 12 2 remarque: La densité d’énergie électrostatique d. W/d 3 r = eo. E 2/2 a les mêmes dimensions qu’une force par unité de surface, c’est à dire d’une pression: [d. W/d 3 r] = [Fdr/d 3 r] = [F/ d 2 r] La quantité eo. E 2/2 représente donc la pression électrostatique exercée à la surface d’un conducteur plongé dans un champ électrique valant E à sa surface. Electromagnétisme - L 2 PCGI - Université Rennes 1 - 2005 51

3. 9 Cas des conducteurs parfaits Systèmes à plus de deux conducteurs: coefficients de capacité Lorsqu’il y a plus de deux conducteurs, on utilise le principe de superposition (des forces, du champ électrique et du potentiel). Supposons qu’il y ait trois conducteurs portés respectivement aux potentiels V 1, V 2 et V 3. Alors tour à tour nous calculons les charges portées par les trois conducteurs lorsque deux des conducteurs sont portés à un potentiel nul: si V 2 = V 3 = 0: Q 1= C 11 V 1 Q 2= C 21 V 1 Q 3= C 31 V 1 si V 3= V 1 = 0: Q 1= C 12 V 2 Q 2= C 22 V 2 Q 3= C 32 V 2 si V 1= V 2 = 0: Q 1= C 13 V 3 Q 2= C 23 V 3 Q 3= C 33 V 3 Lorsque les trois potentiels sont non nuls, les charges sont les sommes des charges précédemment calculées et l’on obtient un système à trois équations: Q 1= C 11 V 1 + C 12 V 2 + C 13 V 3 Q 2= C 21 V 1 + C 22 V 2 + C 23 V 3 Q 3 = C 31 V 1 + C 32 V 2 + C 33 V 3 Les coefficient Cij sont appelés coefficients de capacité. Electromagnétisme - L 2 PCGI - Université Rennes 1 - 2005 52

3. 9 Cas des conducteurs parfaits Courants stationnaires: relation entre densité de charge et densité de courant Des charges libres en mouvement dans un conducteur engendrent des courants. Supposons qu’un courant I traverse une surface S. Ce courant est le flux total de charges qui traverse la surface. Il peut donc être écrit comme l’intégrale du flux d’une densité de courant. Supposons que la surface S soit fermée. Le courant représente la quantité de charge quitte le volume V délimité pas la surface S. On a donc la double égalité: S 3 r·d r t V j·d. S = - On peut utiliser le théorème de la divergence pour ramener la première intégrale à une intégrale en volume de la divergence de j. On peut également inverser l’intégration spatiale et la dérivation par rapport au temps dans la deuxième intégrale. Enfin cette équation doit être vraie quelque soit la surface S et le volume V. Donc l’équation doit être vraie pour les intégrands eux même quelque soit la position. On obtient finalement l’équation de conservation de charge: ·j = Electromagnétisme - L 2 PCGI - Université Rennes 1 - 2005 - r t 53

3. 9 Cas des milieux isolants (diélectriques) Dans les milieux isolants, les charges ne sont pas libres de se déplacer « indéfiniment » lorsqu’elles sont soumises à un champ électrique. Elles sont liées à des « centres attracteurs » et ne peuvent s’écarter plus d’une certaine distance de ces attracteurs, entraînant cependant localement la formation de petits dipôles électriques. Supposons un matériaux homogène de volume donné où ces dipôles de moment dipolaire p sont en concentration n. Le moment dipolaire total P ou Polarisation Electrique de l’échantillon « par unité de volume » vaut: P = np d 3 r’ P r - r’ Le potentiel électrostatique créé par unité de volume est alors donné par : P·(r - r’) 3 r’ d. V( r ) = d 4 peo |r - r’|3 V( r ) valable « loin » du diélectrique !!! Electromagnétisme - L 2 PCGI - Université Rennes 1 - 2005 54

3. 9 Cas des milieux isolants (diélectriques) d 3 r’ On peut transformer cette expression en introduisant le gradient de la fonction 1/r où r ( r’) = |r - r’| : P r - r’ P· ’(1/r) d. V( r ) = d 3 r’ 4 peo V( r ) Par intégration sur tout le volume de diélectrique on obtient : 1 V( r ) = 4 peo 1 3 r’ P· ’ d r Expression que l’on peut transformer en tenant compte de l’identité : • ( f. A ) = ( f ) • A + f • A Electromagnétisme - L 2 PCGI - Université Rennes 1 - 2005 55

3. 9 Cas des milieux isolants (diélectriques) En posant f= 1/r on obtient : 1 V( r ) = 4 peo P 1 3 r’ - ’· d r 4 peo ’·P d 3 r’ r intégrale de volume intégrale de surface 1 V( r ) = 4 peo P·d. S 1 - r 4 peo ’·P d 3 r’ r Or on a déjà vu que le potentiel est de la forme V(r) = (1/ 4 peo ) dq/r Donc si N est le vecteur normal à la surface: P·N représente une densité de charge surfacique de charges liées, tandis que - ’·P représente une densité de charge volumique. Si la polarisation est constante dans l’espace, alors seule la densité de charge surfacique existe. Un diélectrique parallèlépipédique où la polarisation serait perpendiculaire à deux faces se comporte comme un condensateur plan ! Electromagnétisme - L 2 PCGI - Université Rennes 1 - 2005 56

3. 9 Cas des milieux isolants (diélectriques) La conservation de charge, implique si la distribution de charge volumique (de charges liées) est non nulle, il existe un courant de polarisation associé: rliée ·P ·jpol = - = jpol = P t t t Lorsqu’on applique l’équation de Poisson reliant champ électrique et charge, il faut prendre la charge totale, c’est à dire la somme des charges libres et liées. On introduit alors une nouvelle grandeur, appelée Déplacement Electrique l’on note D et qui est définie par: D = eo. E + P ·D = rlibres On peut également dire qu’à l’intérieur d’un diélectrique le champ électrique est la somme de deux contributions: une contribution associées aux charges libres D/eo et une contribution associée aux charges liées -P/eo. Electromagnétisme - L 2 PCGI - Université Rennes 1 - 2005 57

3. 9 Cas des milieux isolants (diélectriques) Sans rentrer dans le détail de l’origine microscopique des dipôles, on peut traiter la polarisation électrique d’un diélectrique dans le cadre de la Réponse Linéaire, c’est à dire qu’on écrit que la réponse « Polarisation » est proportionnelle à l’excitation « champ électrique » : P = E D = eo(1+ )E = eoer E = e E est la susceptibilité électrique er est la permittivité électrique relative du milieu e est la permittivité électrique ou constante diélectrique du matériau Dans le vide =0 et er =1. La plupart des matériaux ont une permittivité relative comprise entre 2 et 5. Cependant on peut trouver des matériaux où cette permittivité relative peut dépasser 105 ! Electromagnétisme - L 2 PCGI - Université Rennes 1 - 2005 58

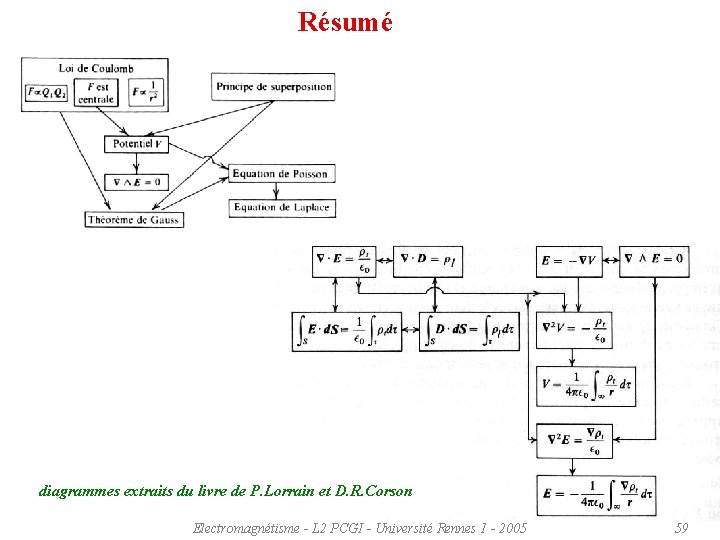
Résumé diagrammes extraits du livre de P. Lorrain et D. R. Corson Electromagnétisme - L 2 PCGI - Université Rennes 1 - 2005 59