TRIGONOMETRA Primera parte Trigonometra es la rama de

TRIGONOMETRÍA (Primera parte)

Trigonometría es la rama de las Matemáticas que trata las relaciones entre los lados y los ángulos de un triángulo. La Trigonometría ayuda a determinar distancias a las que no se puede acceder directamente. Se usa en la navegación, en Agrimensura y en Astronomía. Tiene aplicación en Física, en Química y en Ingeniería, en especial en el estudio de fenómenos periódicos como la vibración del sonido, en el flujo de la corriente alterna, . . . La Trigonometría comenzó con las civilizaciones babilónica y egipcia y se desarrollo en la Antigüedad gracias a los griegos e hindúes. A partir del siglo VIII d. C. , astrónomos islámicos perfeccionaron los conocimientos descubiertos por griegos e hindúes. La Trigonometría moderna comenzó con el trabajo de matemáticos en Occidente a partir del siglo XV. La invención de los logaritmos por el escocés John Naiper y del cálculo diferencial e integral por Isaac Newton ayudaron al progreso de los cálculos trigonométricos. 2

INTRODUCCIÓN Trigonometría significa, etimológicamente, medida de triángulos. En los trabajos topográficos y de la construcción es necesario conocer cotas, desniveles de terreno, etc. , para lo cual se hace imprescindible medir el valor de los ángulos que permiten calcular distancias. El instrumento que se utiliza para medir ángulos en tierra firme es el teodolito. Conociendo algunos elementos de un triángulo- algún lado, algún ángulo- , podremos determinar los restantes. Tales de Mileto (640 -550 a. J. C. ) en uno de sus viajes a Egipto midió la altura de una pirámide aprovechando el momento en que su propia sombra medía tanto como su estatura 3

• NOCIONES PREVIAS • SISTEMAS DE MEDIDA DE ÁNGULOS. RADIÁN. • RAZONES TRIGONOMÉTRICAS (R. T. ) DE UN ÁNGULO AGUDO. • R. T. DE LOS ÁNGULOS 30º, 45º Y 60º. • RELACIÓN FUNDAMENTAL DE TRIGONOMETRÍA • R. T. DE LOS ÁNGULOS 0º Y 90º • CIRCUNFERENCIA GONIOMÉTRICA. 4

NOCIONES PREVIAS 1. a. Proporcionalidad de segmentos y semejanza b. TEOREMA DE TALES 2. TEOREMA DE PITÁGORAS

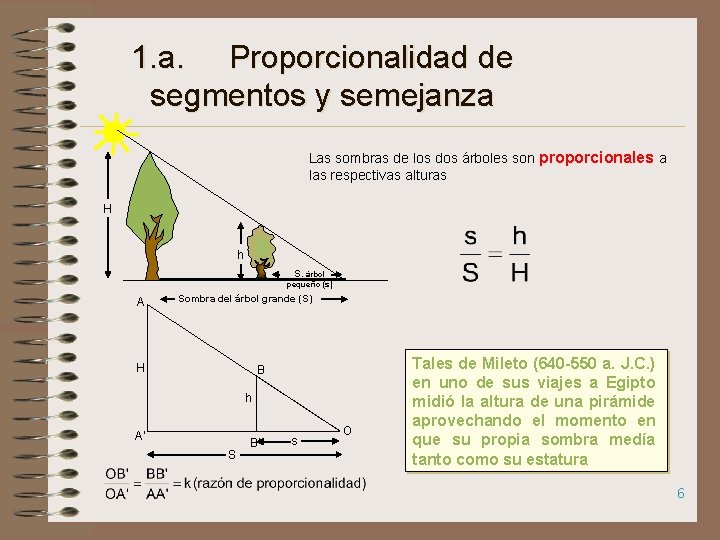
1. a. Proporcionalidad de segmentos y semejanza Las sombras de los dos árboles son proporcionales a las respectivas alturas H h S. árbol pequeño (s) A Sombra del árbol grande (S) H B h A’ S B’ s O Tales de Mileto (640 -550 a. J. C. ) en uno de sus viajes a Egipto midió la altura de una pirámide aprovechando el momento en que su propia sombra medía tanto como su estatura 6

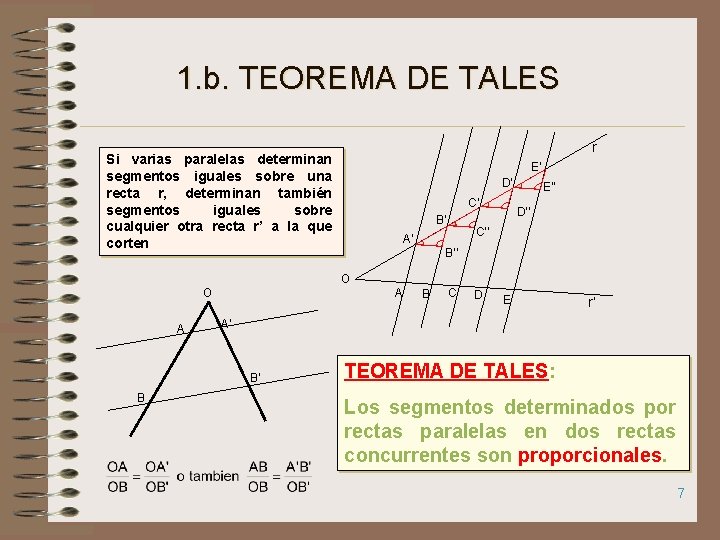
1. b. TEOREMA DE TALES r Si varias paralelas determinan segmentos iguales sobre una recta r, determinan también segmentos iguales sobre cualquier otra recta r’ a la que corten E’ D’ C’ B’ E’’ D’’ C’’ A’ B’’ O A C D E r’ A’ B’ B B TEOREMA DE TALES: Los segmentos determinados por rectas paralelas en dos rectas concurrentes son proporcionales. 7

Medida de ángulos Los ángulos pueden medirse en tres sistemas: Sistema sexagesimal (En la calculadora MODE DEG) Sistema centesimal (En la calculadora MODE GRAD) Radianes (En la calculadora MODE RAD) Ángulo de 1 giro Ángulo llano Ángulo recto Un grado Un minuto SEXAGESIMAL 360º 180º 90º 60’ 60” CENTESIMAL 400 g 200 g 100 m 100 s 2 /2 RADIANES 8

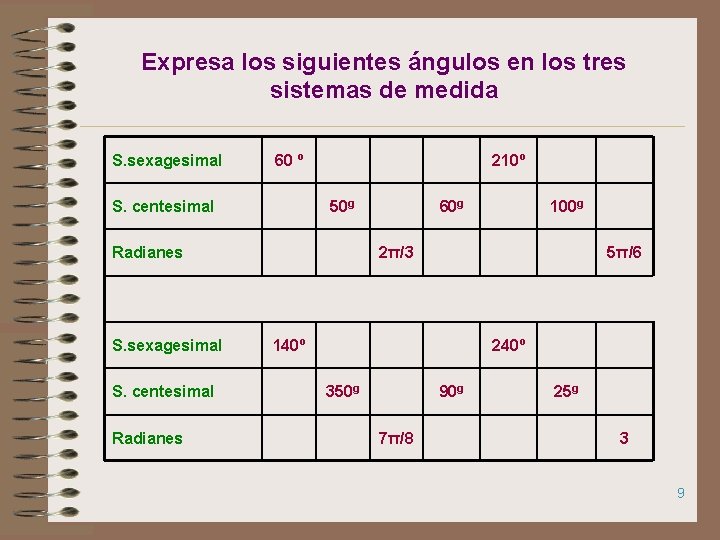
Expresa los siguientes ángulos en los tres sistemas de medida S. sexagesimal 60 º S. centesimal 210º 50 g Radianes S. sexagesimal S. centesimal Radianes 60 g 100 g 2π/3 5π/6 140º 240º 350 g 90 g 7π/8 25 g 3 9

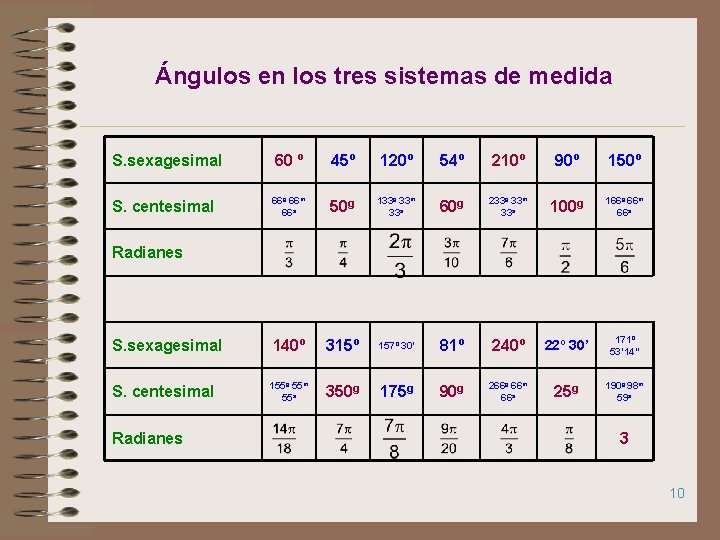
Ángulos en los tres sistemas de medida S. sexagesimal 60 º 45º 120º 54º 210º 90º 150º S. centesimal 66 g 66 m 66 s 50 g 133 g 33 m 33 s 60 g 233 g 33 m 33 s 100 g 166 g 66 m 66 s 140º 315º 157º 30’ 81º 240º 22º 30’ 171º 53’ 14” 155 g 55 m 55 s 350 g 175 g 90 g 266 g 66 m 66 s 25 g 190 g 98 m 59 s Radianes S. sexagesimal S. centesimal Radianes 3 10

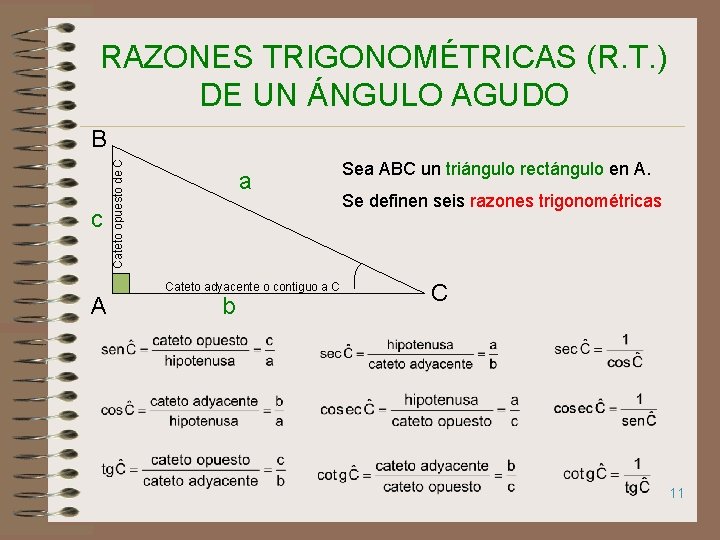
RAZONES TRIGONOMÉTRICAS (R. T. ) DE UN ÁNGULO AGUDO c A Cateto opuesto de C B a Cateto adyacente o contiguo a C b Sea ABC un triángulo rectángulo en A. Se definen seis razones trigonométricas C 11

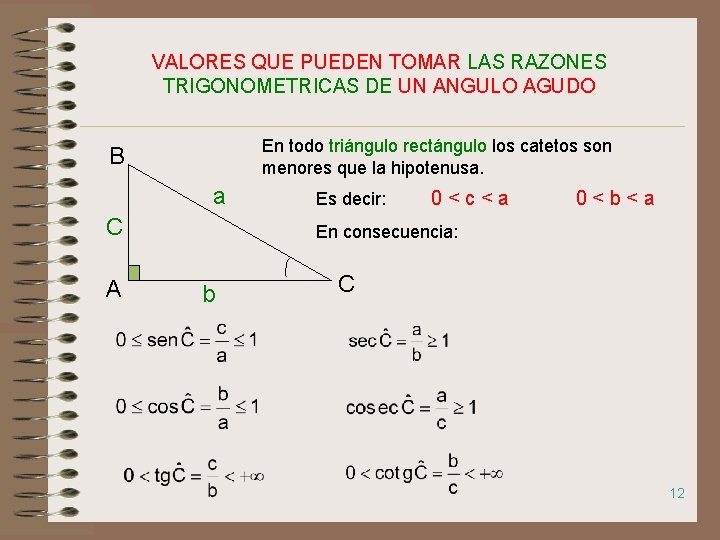
VALORES QUE PUEDEN TOMAR LAS RAZONES TRIGONOMETRICAS DE UN ANGULO AGUDO En todo triángulo rectángulo los catetos son menores que la hipotenusa. B a C A Es decir: 0<c<a 0<b<a En consecuencia: b C 12

RAZONES TRIGONOMÉTRICAS DE 30º, 45º y 60º 1. R. T. DE 30º y 60º 2. R. T. DE 45º

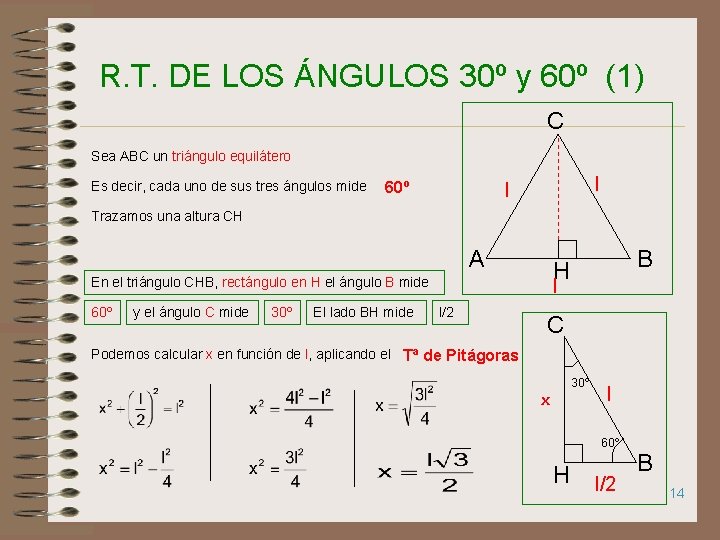
R. T. DE LOS ÁNGULOS 30º y 60º (1) C Sea ABC un triángulo equilátero Es decir, cada uno de sus tres ángulos mide 60º l l Trazamos una altura CH A En el triángulo CHB, rectángulo en H el ángulo B mide 60º y el ángulo C mide 30º El lado BH mide B H l l/2 C Podemos calcular x en función de l, aplicando el Tª de Pitágoras 30º x l 60º H l/2 B 14

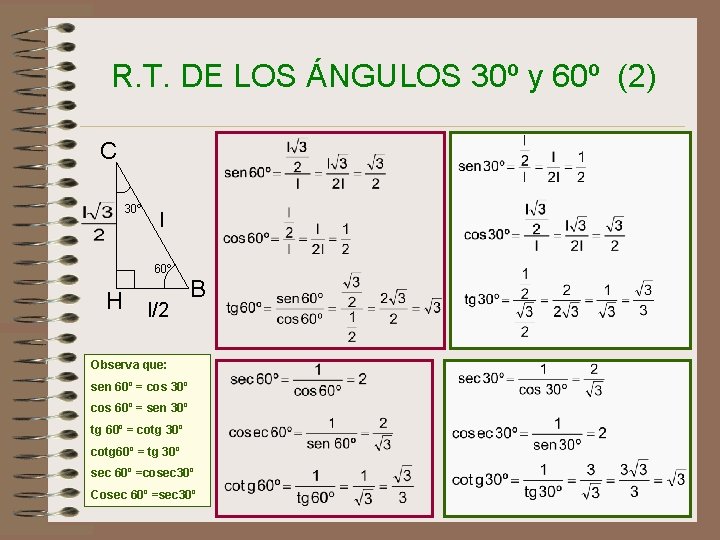
R. T. DE LOS ÁNGULOS 30º y 60º (2) C 30º l 60º H l/2 B Observa que: sen 60º = cos 30º cos 60º = sen 30º tg 60º = cotg 30º cotg 60º = tg 30º sec 60º =cosec 30º Cosec 60º =sec 30º 15

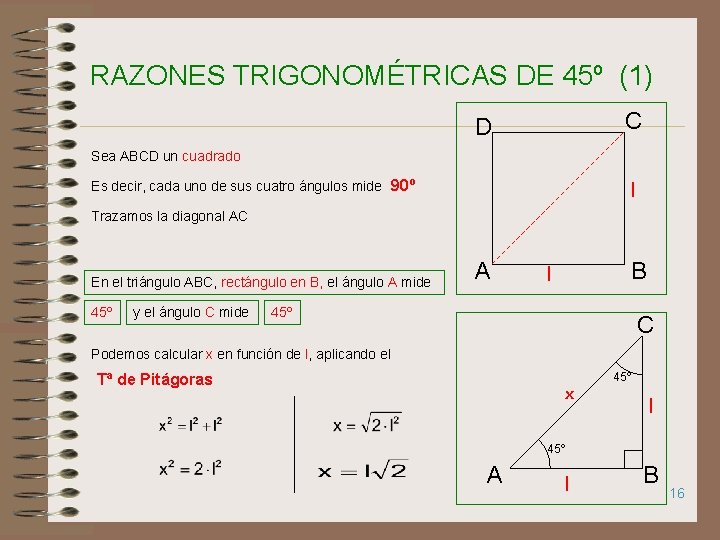
RAZONES TRIGONOMÉTRICAS DE 45º (1) C D Sea ABCD un cuadrado Es decir, cada uno de sus cuatro ángulos mide 90º l Trazamos la diagonal AC En el triángulo ABC, rectángulo en B, el ángulo A mide 45º y el ángulo C mide A B l 45º C Podemos calcular x en función de l, aplicando el Tª de Pitágoras x 45º l 45º A l B 16

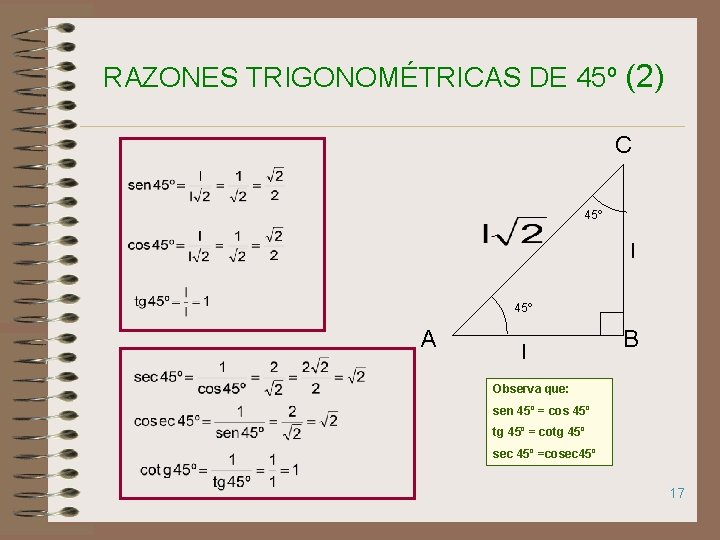
RAZONES TRIGONOMÉTRICAS DE 45º (2) C 45º l 45º A l B Observa que: sen 45º = cos 45º tg 45º = cotg 45º sec 45º =cosec 45º 17

R. T. DE ÁNGULOS COMPLEMENTARIOS C Sea ABC un triángulo rectángulo ABC, rectángulo en A Si el ángulo B mide α grados, a b el ángulo C mide α B c A 18

RELACIÓN FUNDAMENTAL DE TRIGONOMETRÍA Si en el triángulo rectángulo BAC, aplicamos el teorema de Pitágoras, tenemos: Si dividimos la expresión anterior por a 2 Expresándolo de otra forma: C a B b α c A O lo que es lo mismo: Que normalmente expresaremos de la forma: 19

OTRAS RELACIONES FUNDAMENTALES C Si en el triángulo rectángulo BAC, aplicamos el teorema de Pitágoras, tenemos: B Si dividimos la expresión anterior por b 2 o por c 2 a b c A α Expresándolo de otra forma: 20

Circunferencia goniométrica 1. R. T. DE ÁNGULO CUALQUIERA 2. VALORES Y SIGNO DEL SENO Y DEL COSENO DE UN ÁNGULO 3. VALORES Y SIGNO DE LA TANGENTE Y DE LA COTANGENTE 4. R. T. DE ÁNGULOS SUPLEMENTARIOS 5. R. T. DE ÁNGULOS QUE DIFIEREN EN 180º 6. R. T. DE ÁNGULOS QUE SUMAN 360º 7. R. T. DE ÁNGULOS OPUESTOS

CIRCUNFERENCIA GONIOMÉTRICA Trazamos una circunferencia de radio 1 y centro en el origen de un sistema de coordenadas Uno de los lados del ángulo Y deberá coincidir con el semieje positivo de las x, el vértice en el origen de coordenadas y el otro lado donde corresponda a O 1 X A esta circunferencia donde situaremos los ángulos la llamaremos circunferencia goniométrica. 22

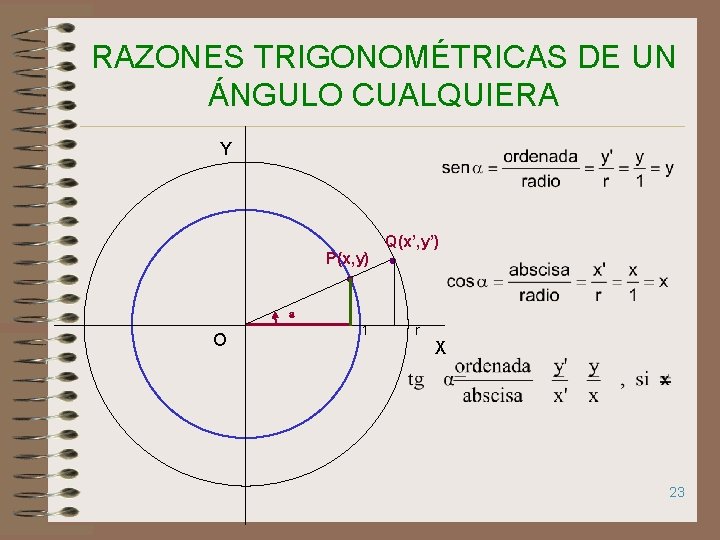
RAZONES TRIGONOMÉTRICAS DE UN ÁNGULO CUALQUIERA Y P(x, y) a O 1 Q(x’, y’) r X 23

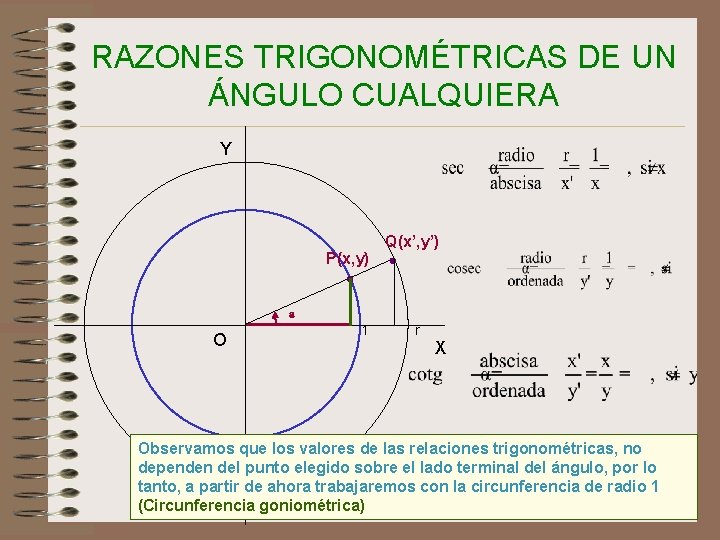
RAZONES TRIGONOMÉTRICAS DE UN ÁNGULO CUALQUIERA Y P(x, y) a O 1 Q(x’, y’) r X Observamos que los valores de las relaciones trigonométricas, no dependen del punto elegido sobre el lado terminal del ángulo, por lo tanto, a partir de ahora trabajaremos con la circunferencia de radio 1 24 (Circunferencia goniométrica)

RAZONES TRIGONOMÉTRICAS DE UN ÁNGULO CUALQUIERA 25

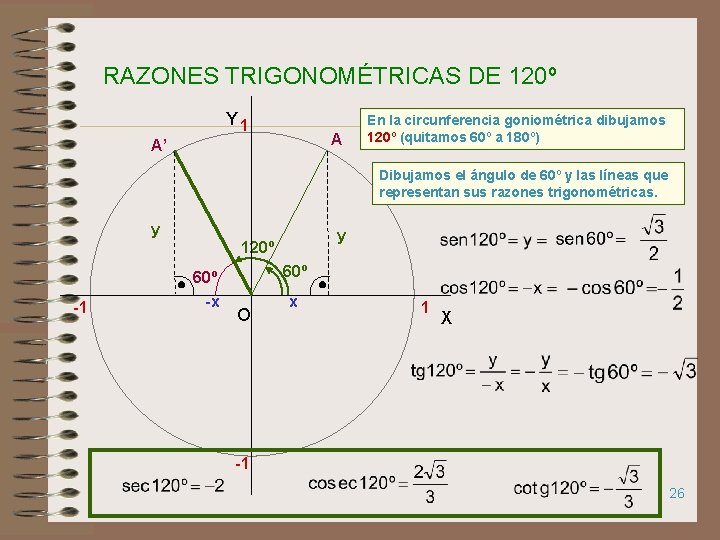
RAZONES TRIGONOMÉTRICAS DE 120º Y 1 A A’ En la circunferencia goniométrica dibujamos 120º (quitamos 60º a 180º) Dibujamos el ángulo de 60º y las líneas que representan sus razones trigonométricas. y y 120º -1 60º -x 60º O x 1 X -1 26

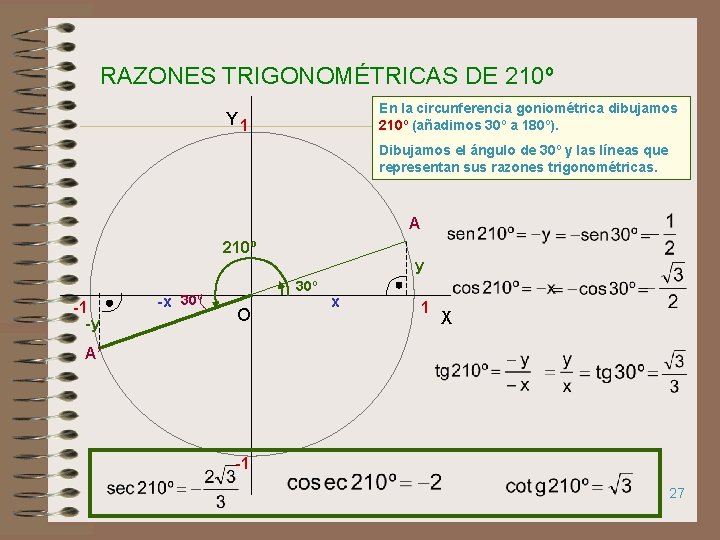
RAZONES TRIGONOMÉTRICAS DE 210º En la circunferencia goniométrica dibujamos 210º (añadimos 30º a 180º). Y 1 Dibujamos el ángulo de 30º y las líneas que representan sus razones trigonométricas. A 210º y -1 -y -x 30º O x 1 X A’ -1 27

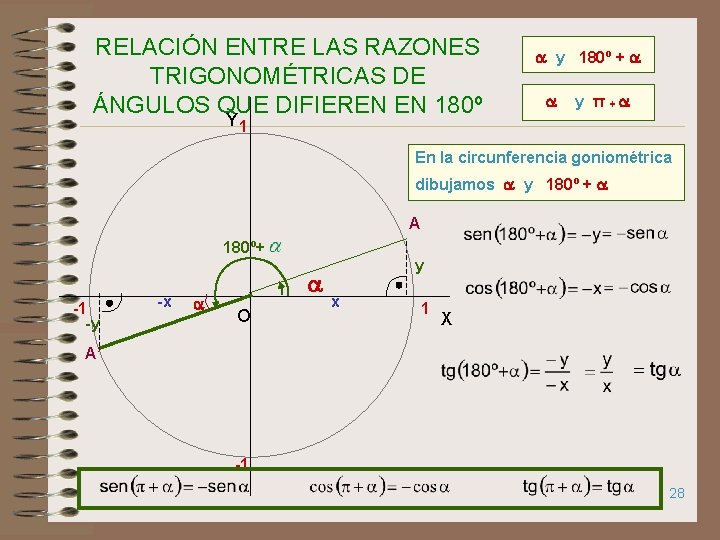
RELACIÓN ENTRE LAS RAZONES TRIGONOMÉTRICAS DE ÁNGULOS QUE DIFIEREN EN 180º Y 1 y 180º + y π+ En la circunferencia goniométrica dibujamos y 180º + A 180º+ -1 -y -x O y x 1 X A’ -1 28

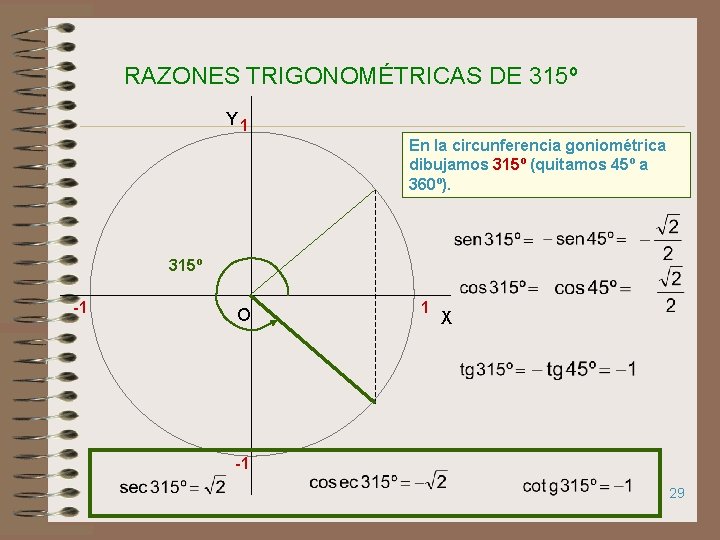
RAZONES TRIGONOMÉTRICAS DE 315º Y 1 En la circunferencia goniométrica dibujamos 315º (quitamos 45º a 360º). 315º -1 O 1 X -1 29

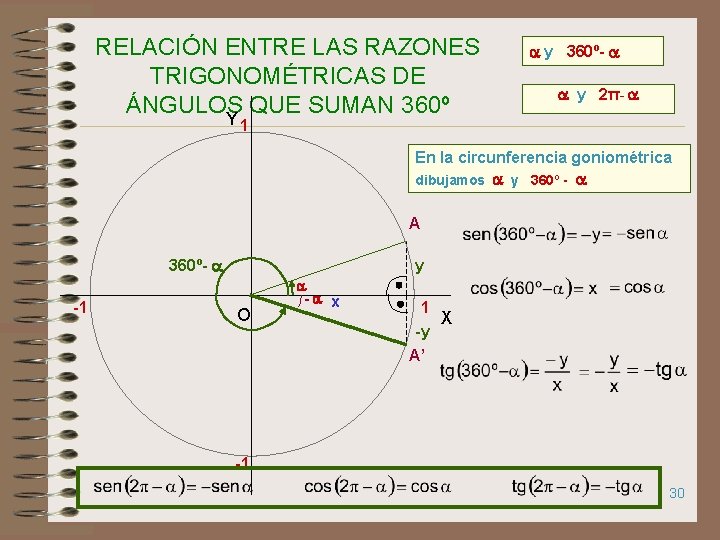
RELACIÓN ENTRE LAS RAZONES TRIGONOMÉTRICAS DE ÁNGULOS QUE SUMAN 360º y 360º- y 2π- Y 1 En la circunferencia goniométrica dibujamos y 360º - A 360º- y -1 O - x 1 X -y A’ -1 30

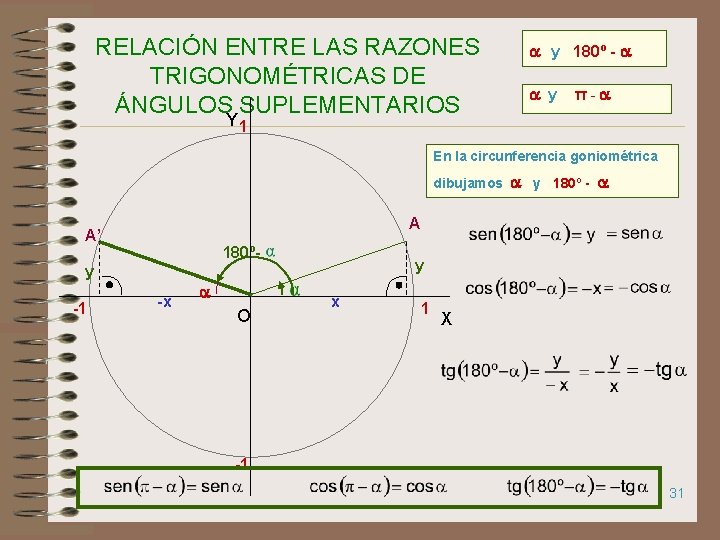
RELACIÓN ENTRE LAS RAZONES TRIGONOMÉTRICAS DE ÁNGULOS SUPLEMENTARIOS y 180º - y π- Y 1 En la circunferencia goniométrica dibujamos y 180º - A A’ 180º- y -1 -x O y x 1 X -1 31

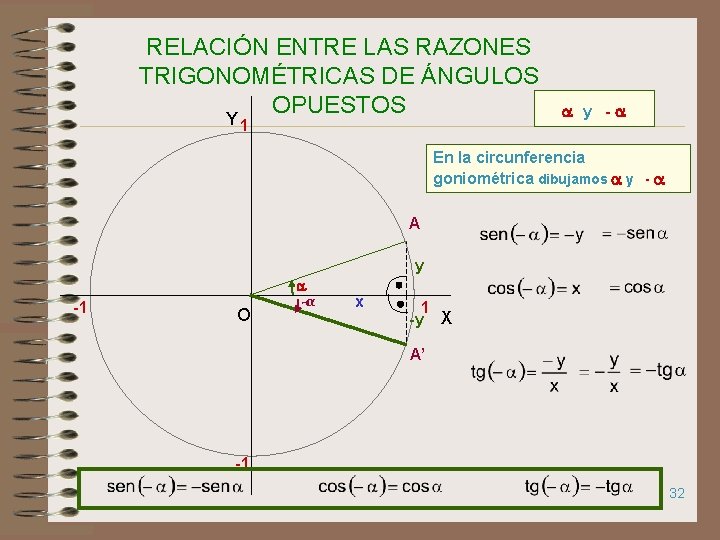
RELACIÓN ENTRE LAS RAZONES TRIGONOMÉTRICAS DE ÁNGULOS OPUESTOS Y 1 y - En la circunferencia goniométrica dibujamos y - A y -1 O -α x 1 -y X A’ -1 32

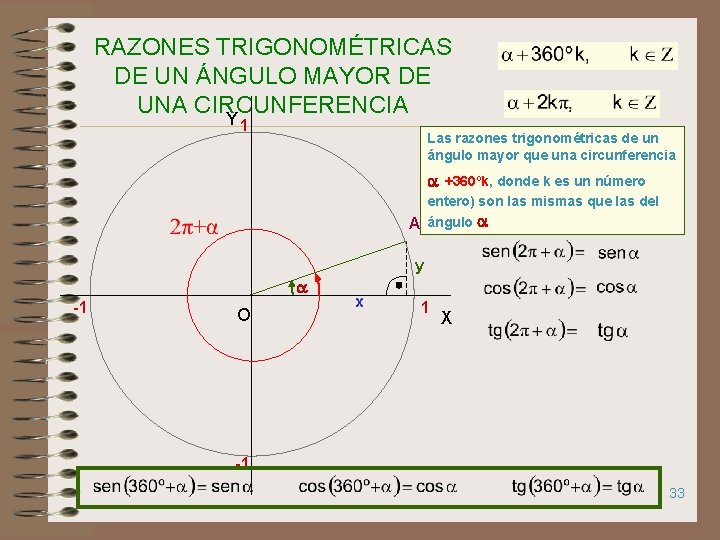
RAZONES TRIGONOMÉTRICAS DE UN ÁNGULO MAYOR DE UNA CIRCUNFERENCIA Y 1 Las razones trigonométricas de un ángulo mayor que una circunferencia +360ºk, donde k es un número entero) son las mismas que las del A ángulo y -1 O x 1 X -1 33

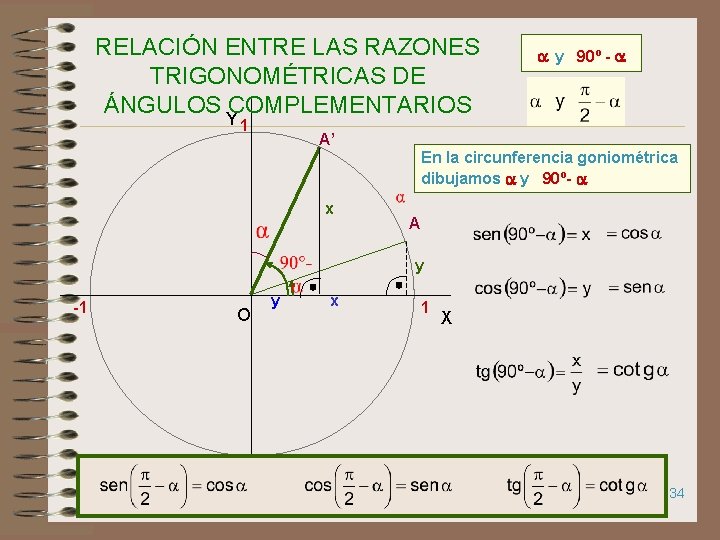
RELACIÓN ENTRE LAS RAZONES TRIGONOMÉTRICAS DE ÁNGULOS COMPLEMENTARIOS Y 1 y 90º - A’ En la circunferencia goniométrica dibujamos y 90º- x A y -1 O y x 1 X -1 34

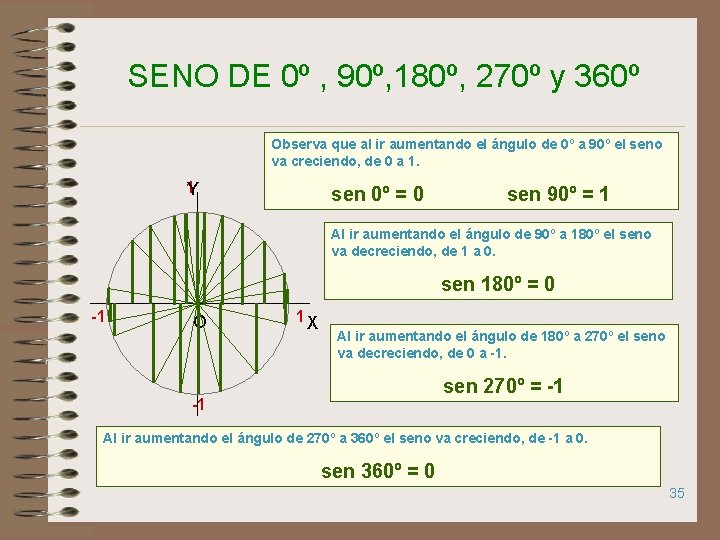
SENO DE 0º , 90º, 180º, 270º y 360º Observa que al ir aumentando el ángulo de 0º a 90º el seno va creciendo, de 0 a 1. 1 Y sen 0º = 0 sen 90º = 1 Al ir aumentando el ángulo de 90º a 180º el seno va decreciendo, de 1 a 0. sen 180º = 0 -1 O 1 X Al ir aumentando el ángulo de 180º a 270º el seno va decreciendo, de 0 a -1. sen 270º = -1 -1 Al ir aumentando el ángulo de 270º a 360º el seno va creciendo, de -1 a 0. sen 360º = 0 35

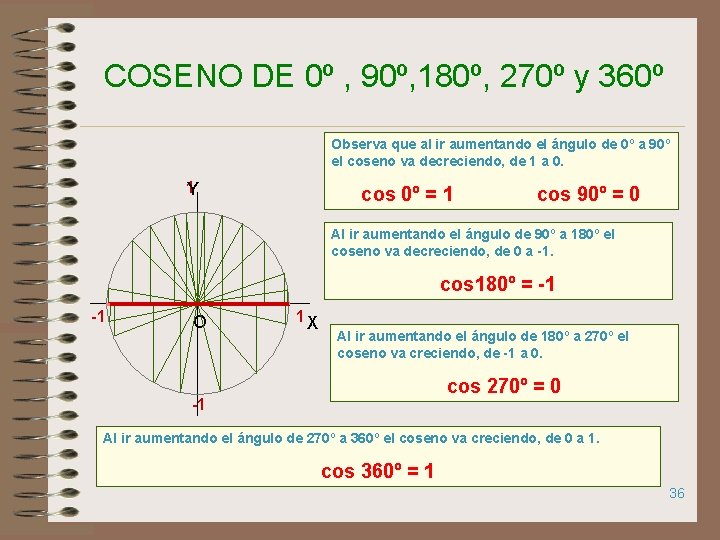
COSENO DE 0º , 90º, 180º, 270º y 360º Observa que al ir aumentando el ángulo de 0º a 90º el coseno va decreciendo, de 1 a 0. 1 Y cos 0º = 1 cos 90º = 0 Al ir aumentando el ángulo de 90º a 180º el coseno va decreciendo, de 0 a -1. cos 180º = -1 -1 O 1 X Al ir aumentando el ángulo de 180º a 270º el coseno va creciendo, de -1 a 0. cos 270º = 0 -1 Al ir aumentando el ángulo de 270º a 360º el coseno va creciendo, de 0 a 1. cos 360º = 1 36

TANGENTE DE 0º , 90º, 180º, 270º y 360º Recordemos que siendo P(x, y) un punto sobre el lado terminal del ángulo, con x≠ 0. Entonces tg 0º= 0 tg 180º=0 tg 360º=0 ya que cualquier punto sobre el lado terminal tiene ordenada 0 y abscisa distinta de 0. tg 90º y tg 270º no están definidas ya que cualquier punto sobre el lado terminal tiene abscisa 0. 37

FUNCIONES TRIGONOMÉTRICAS 1. FUNCIÓN SENO 2. FUNCIÓN COSENO 3. FUNCIÓN TANGENTE 4. FUNCIÓN COTANGENTE 5. FUNCIÓN SECANTE 6. FUNCIÓN COSECANTE

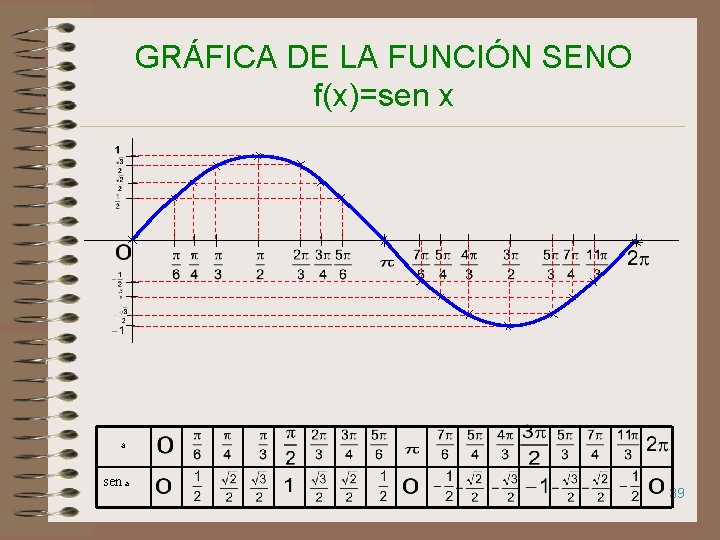
GRÁFICA DE LA FUNCIÓN SENO f(x)=sen x a sen a 39

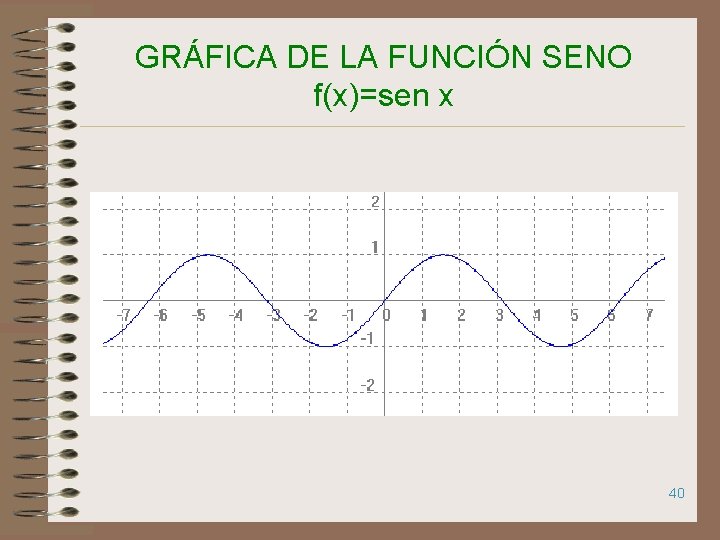
GRÁFICA DE LA FUNCIÓN SENO f(x)=sen x 40

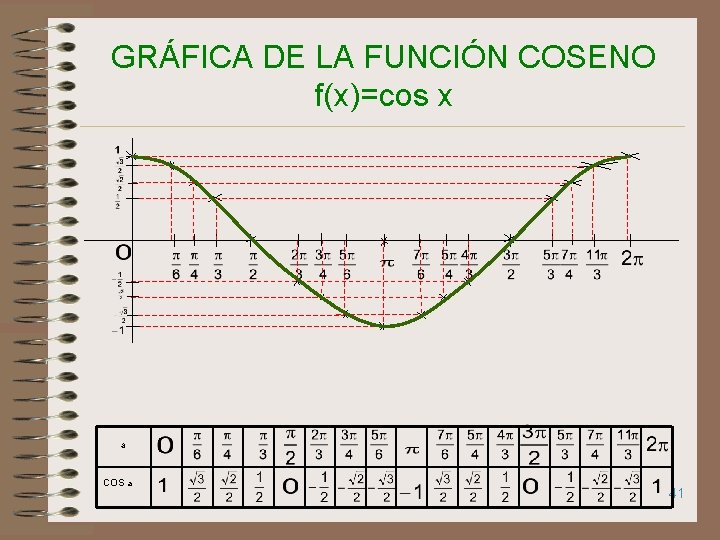
GRÁFICA DE LA FUNCIÓN COSENO f(x)=cos x a COS a 41

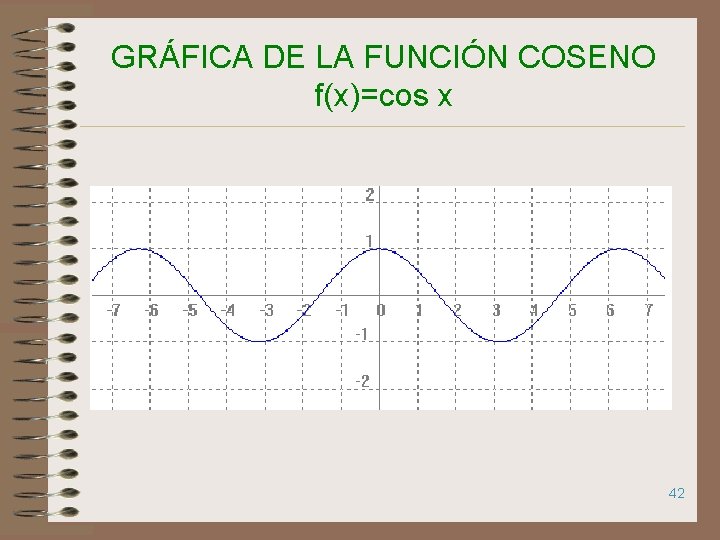
GRÁFICA DE LA FUNCIÓN COSENO f(x)=cos x 42

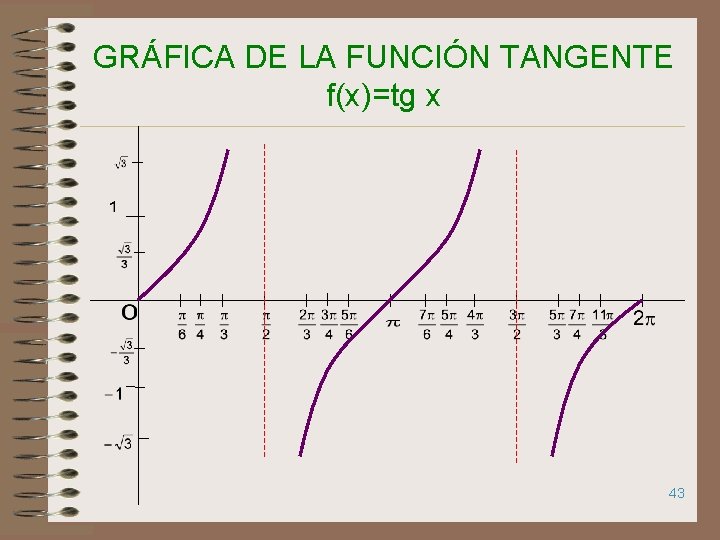
GRÁFICA DE LA FUNCIÓN TANGENTE f(x)=tg x 43

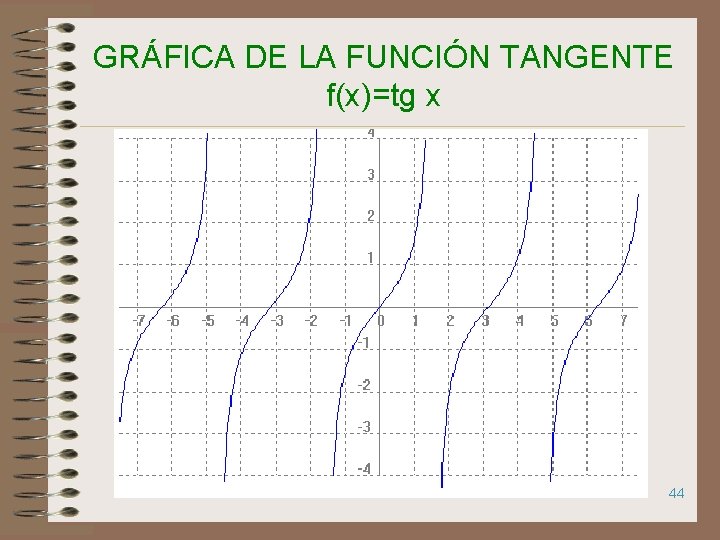
GRÁFICA DE LA FUNCIÓN TANGENTE f(x)=tg x 44

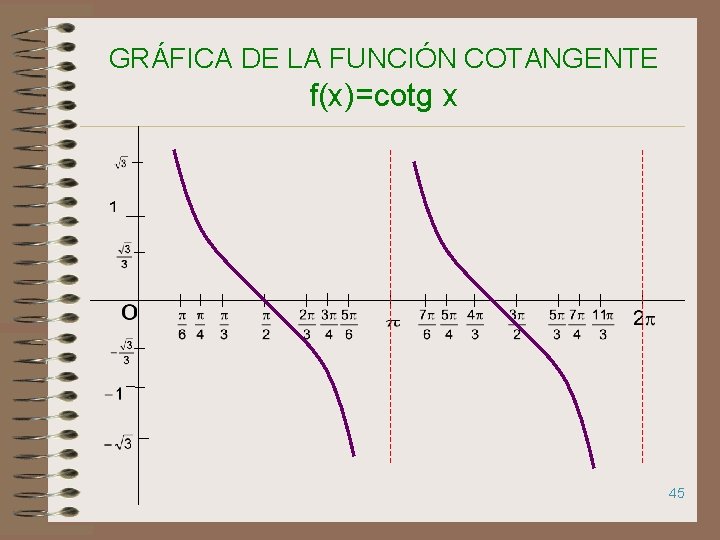
GRÁFICA DE LA FUNCIÓN COTANGENTE f(x)=cotg x 45

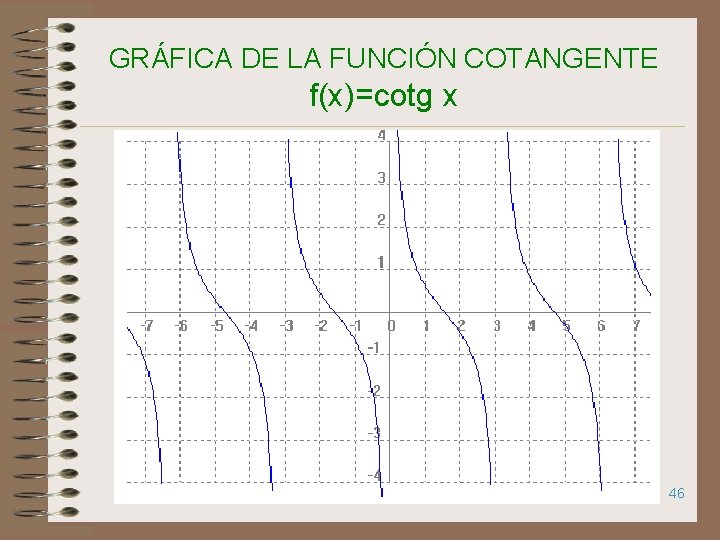
GRÁFICA DE LA FUNCIÓN COTANGENTE f(x)=cotg x 46

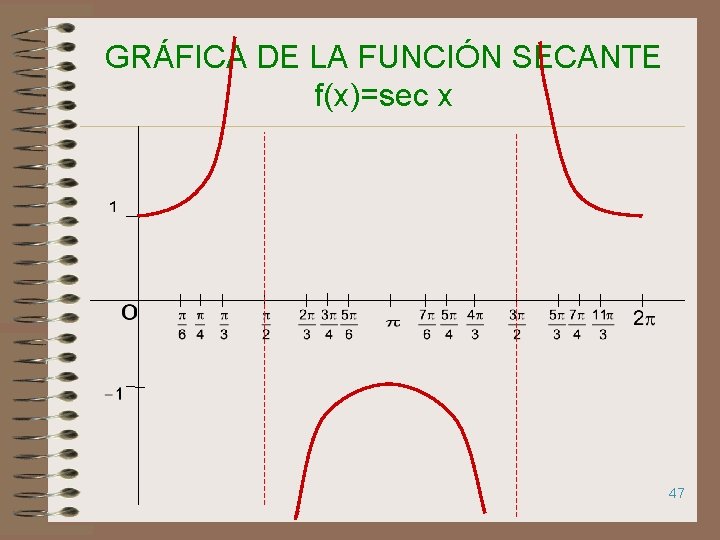
GRÁFICA DE LA FUNCIÓN SECANTE f(x)=sec x 47

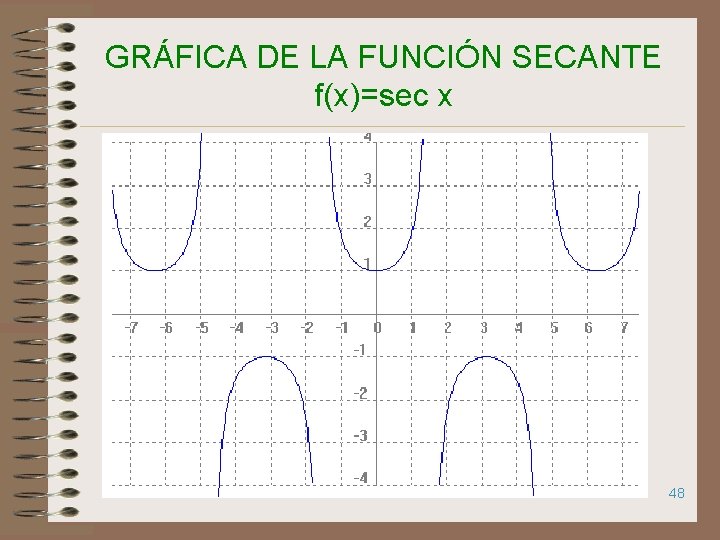
GRÁFICA DE LA FUNCIÓN SECANTE f(x)=sec x 48

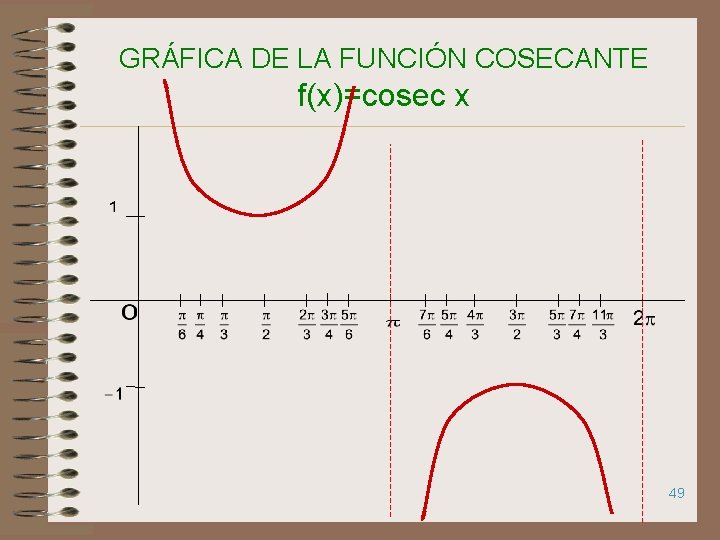
GRÁFICA DE LA FUNCIÓN COSECANTE f(x)=cosec x 49

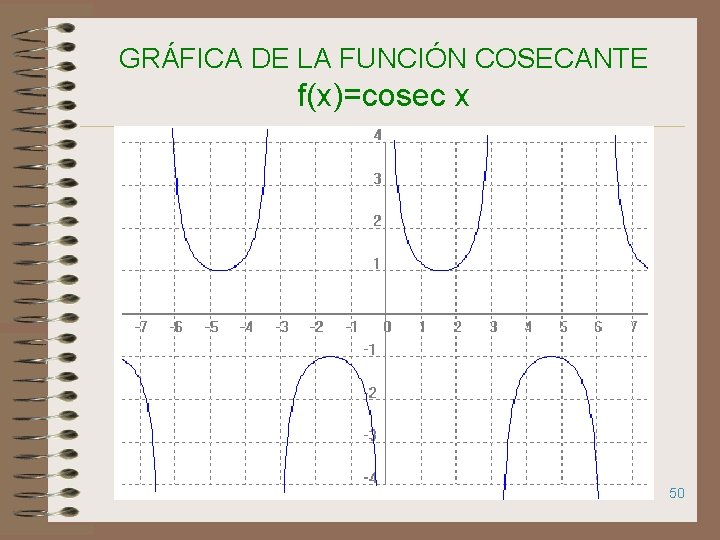
GRÁFICA DE LA FUNCIÓN COSECANTE f(x)=cosec x 50

TRIGONOMETRÍA (Segunda parte)

INTRODUCCIÓN Trigonometría significa, etimológicamente, medida de triángulos. En los trabajos topográficos y de la construcción es necesario conocer cotas, desniveles de terreno, etc. , para lo cual se hace imprescindible medir el valor de los ángulos que permiten calcular distancias. El instrumento que se utiliza para medir ángulos en tierra firme es el teodolito. Conociendo algunos elementos de un triángulo- algún lado, algún ángulo- , podremos determinar los restantes. Tales de Mileto (640 -550 a. J. C. ) en uno de sus viajes a Egipto midió la altura de una pirámide aprovechando el momento en que su propia sombra medía tanto como su estatura 52

1. RAZONES TRIGONOMÉTRICAS DE LA SUMA Y DE LA DIFERENCIA DE ÁNGULOS 2. R. T. DEL ÁNGULO DOBLE. 3. R. T. DEL ÁNGULO MITAD 4. TEOREMA DEL SENO 5. TEOREMA DEL COSENO 6. ÁREA DE UN TRIÁNGULO. FÓRMULA DE HERON

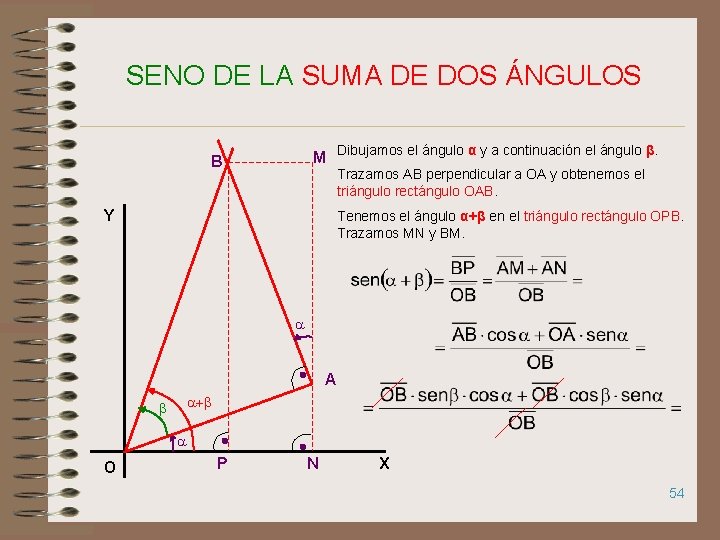
SENO DE LA SUMA DE DOS ÁNGULOS M Dibujamos el ángulo α y a continuación el ángulo β. B Trazamos AB perpendicular a OA y obtenemos el triángulo rectángulo OAB. Y Tenemos el ángulo α+β en el triángulo rectángulo OPB. Trazamos MN y BM. a A a+b b a O P N X 54

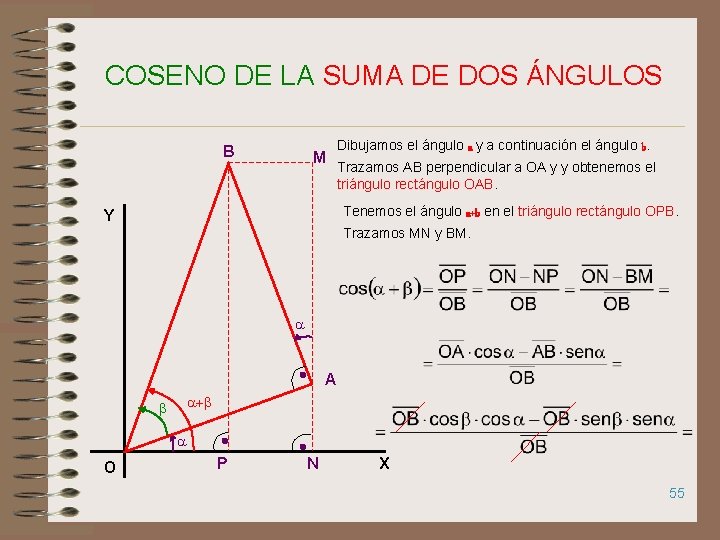
COSENO DE LA SUMA DE DOS ÁNGULOS B M Dibujamos el ángulo a y a continuación el ángulo b. Trazamos AB perpendicular a OA y y obtenemos el triángulo rectángulo OAB. Tenemos el ángulo a+b en el triángulo rectángulo OPB. Y Trazamos MN y BM. a A a+b b a O P N X 55

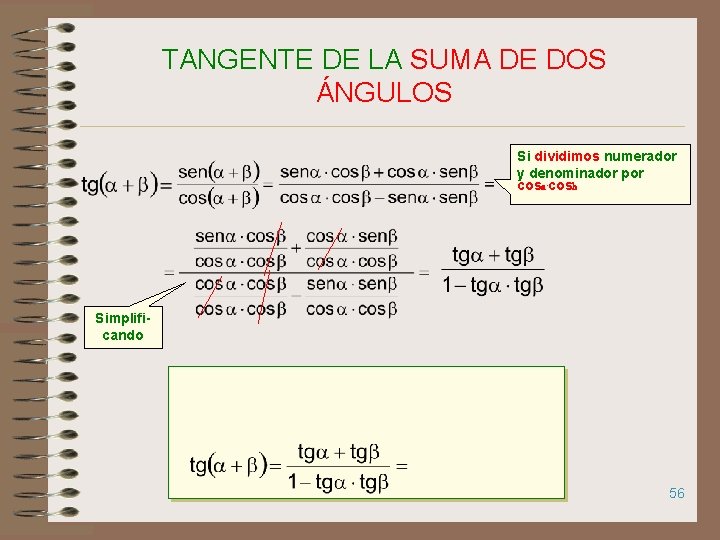
TANGENTE DE LA SUMA DE DOS ÁNGULOS Si dividimos numerador y denominador por cosa. cosb Simplificando 56

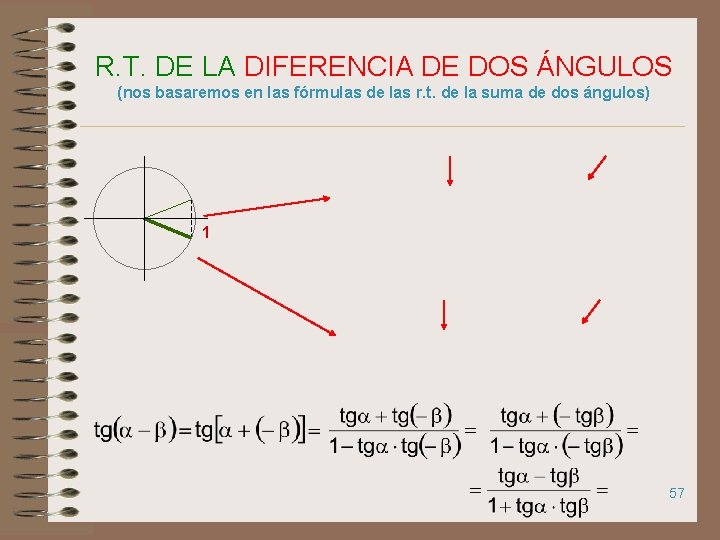
R. T. DE LA DIFERENCIA DE DOS ÁNGULOS (nos basaremos en las fórmulas de las r. t. de la suma de dos ángulos) 1 57

R. T. DE LA SUMA Y DIFERENCIA DE DOS ÁNGULOS 58

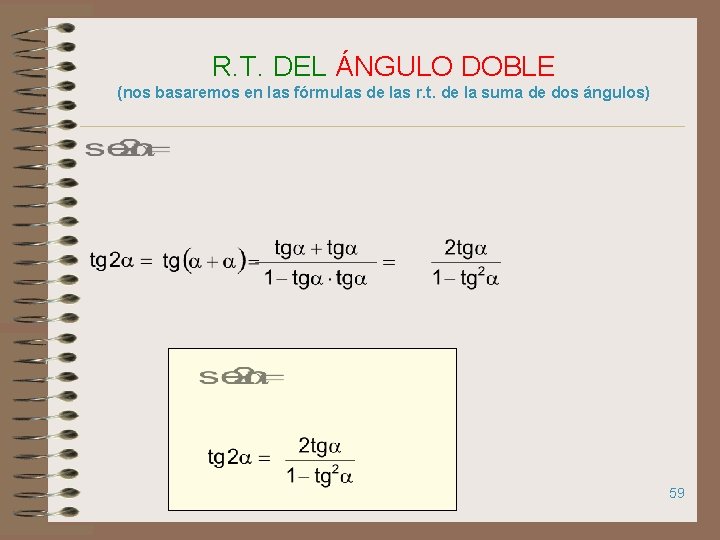
R. T. DEL ÁNGULO DOBLE (nos basaremos en las fórmulas de las r. t. de la suma de dos ángulos) 59

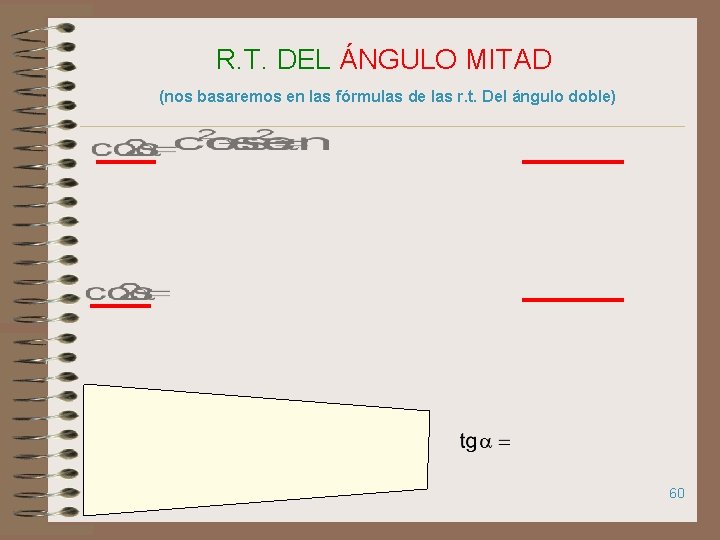
R. T. DEL ÁNGULO MITAD (nos basaremos en las fórmulas de las r. t. Del ángulo doble) 60

1. Teorema del seno 2. Teorema del coseno

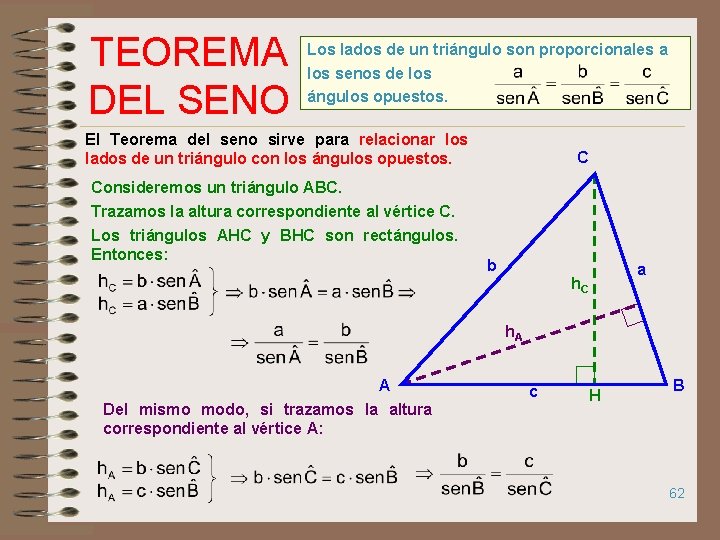
TEOREMA DEL SENO Los lados de un triángulo son proporcionales a los senos de los ángulos opuestos. El Teorema del seno sirve para relacionar los lados de un triángulo con los ángulos opuestos. Consideremos un triángulo ABC. Trazamos la altura correspondiente al vértice C. Los triángulos AHC y BHC son rectángulos. Entonces: C b a h. C h. A A Del mismo modo, si trazamos la altura correspondiente al vértice A: c H B 62

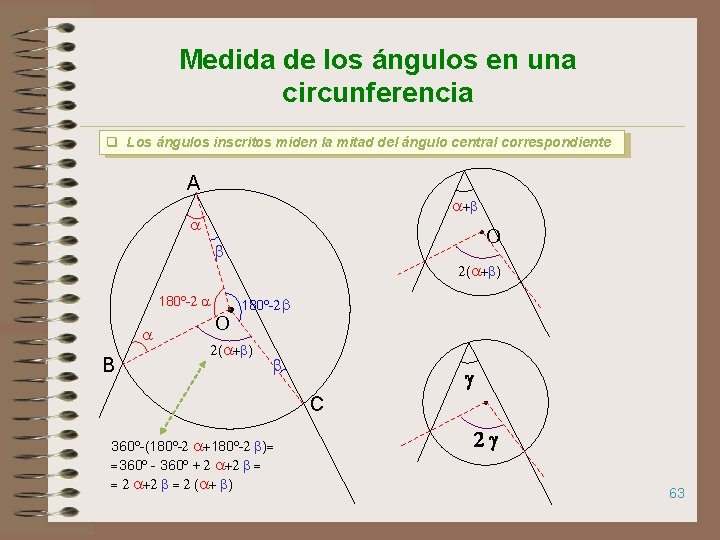
Medida de los ángulos en una circunferencia q Los ángulos inscritos miden la mitad del ángulo central correspondiente A a+b a O b 180º-2 a a B O 2(a+b) 180º-2 b 2(a+b) b g C 360º-(180º-2 a+180º-2 b)= =360º - 360º + 2 a+2 b = = 2 a+2 b = 2 (a+ b) 2 g 63

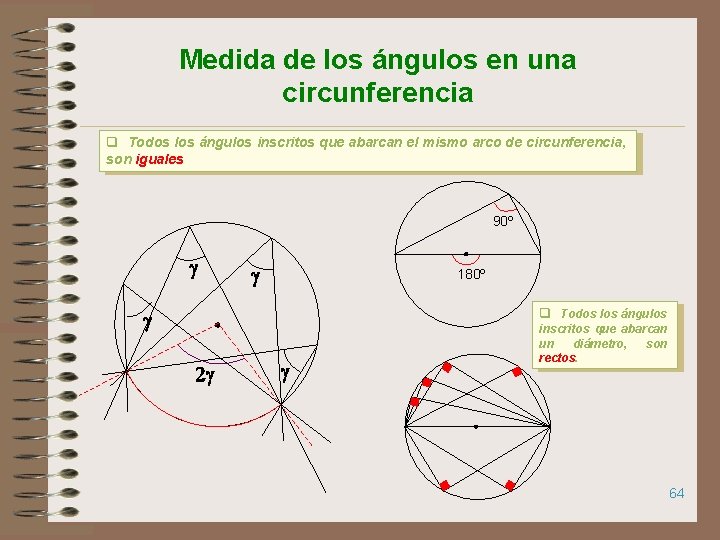
Medida de los ángulos en una circunferencia q Todos los ángulos inscritos que abarcan el mismo arco de circunferencia, son iguales 90º g g 180º q Todos los ángulos g 2 g g inscritos que abarcan un diámetro, son rectos. 64

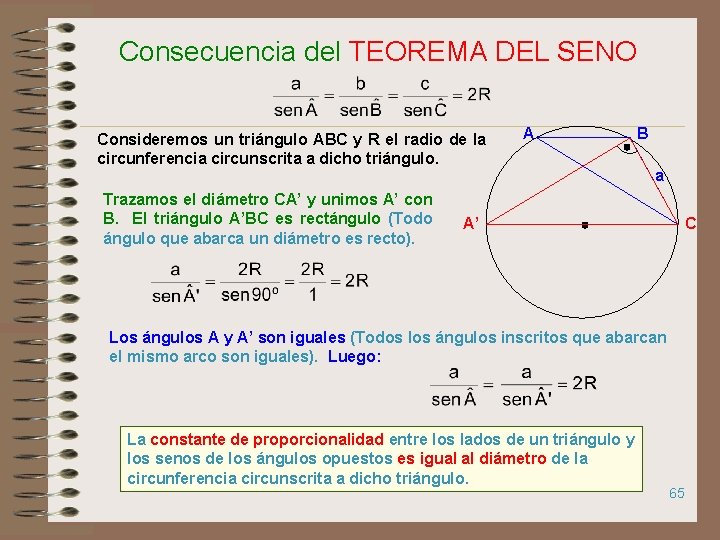
Consecuencia del TEOREMA DEL SENO Consideremos un triángulo ABC y R el radio de la circunferencia circunscrita a dicho triángulo. Trazamos el diámetro CA’ y unimos A’ con B. El triángulo A’BC es rectángulo (Todo ángulo que abarca un diámetro es recto). A B a A’ C Los ángulos A y A’ son iguales (Todos los ángulos inscritos que abarcan el mismo arco son iguales). Luego: La constante de proporcionalidad entre los lados de un triángulo y los senos de los ángulos opuestos es igual al diámetro de la circunferencia circunscrita a dicho triángulo. 65

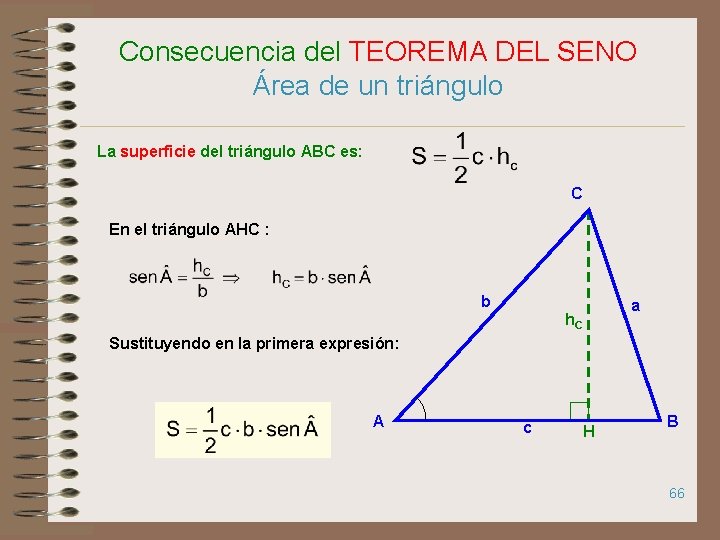
Consecuencia del TEOREMA DEL SENO Área de un triángulo La superficie del triángulo ABC es: C En el triángulo AHC : b a h. C Sustituyendo en la primera expresión: A c H B 66

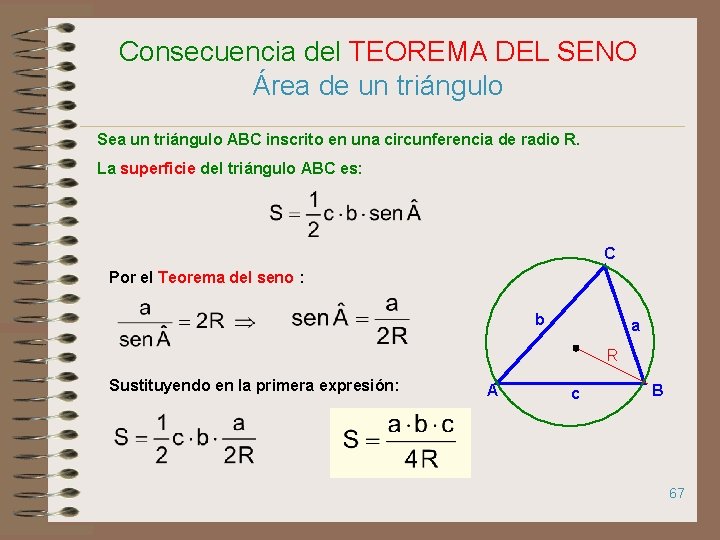
Consecuencia del TEOREMA DEL SENO Área de un triángulo Sea un triángulo ABC inscrito en una circunferencia de radio R. La superficie del triángulo ABC es: C Por el Teorema del seno : b a R Sustituyendo en la primera expresión: A c B 67

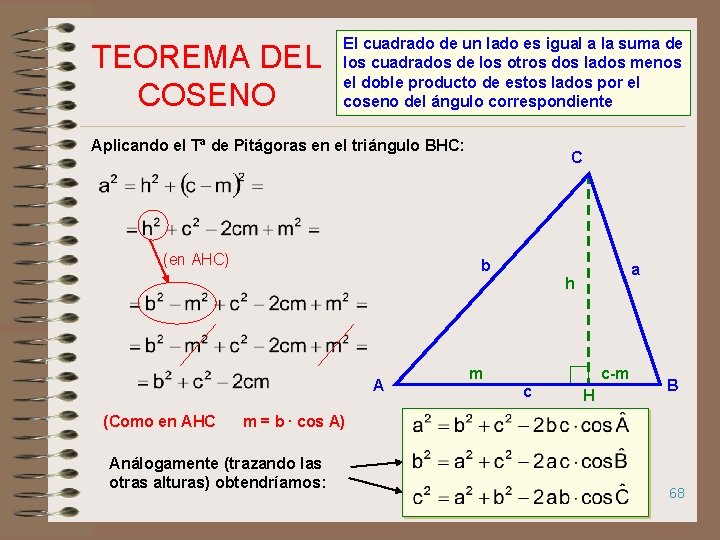
TEOREMA DEL COSENO El cuadrado de un lado es igual a la suma de los cuadrados de los otros dos lados menos el doble producto de estos lados por el coseno del ángulo correspondiente Aplicando el Tª de Pitágoras en el triángulo BHC: (en AHC) C b a h A (Como en AHC m c-m c H B m = b. cos A) Análogamente (trazando las otras alturas) obtendríamos: 68

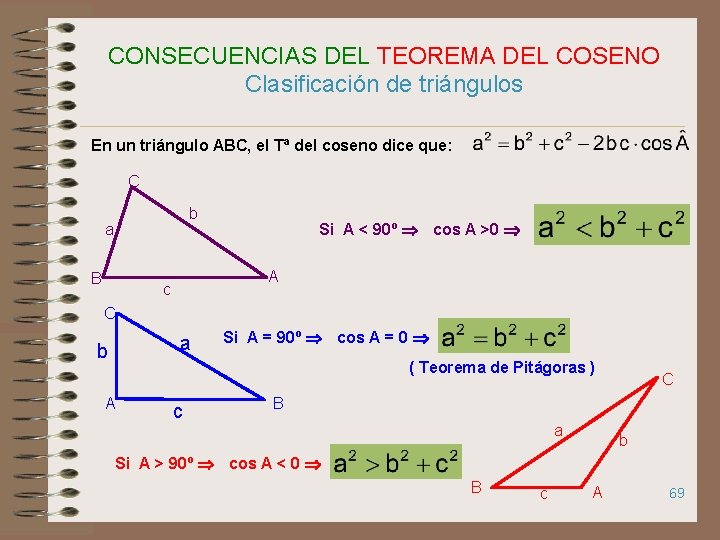
CONSECUENCIAS DEL TEOREMA DEL COSENO Clasificación de triángulos En un triángulo ABC, el Tª del coseno dice que: C b a B Si A < 90º cos A >0 A c C b A a Si A = 90º cos A = 0 ( Teorema de Pitágoras ) c Si A > 90º C B a b cos A < 0 B c A 69