Introduccin a la trigonometra y a las funciones

Introducción a la trigonometría y a las funciones trigonométricas Shirley Bromberg Raquel Valdés

Un poquito de historia Trigonometría es una palabra de etimología griega, aunque no es una palabra griega. Se compone de trigonon que significa triángulo y metria que significa medición. Y se habla de ella como matemática práctica.

La trigonometría resuelve el siguiente problema: conocidos algunas de las componentes de un triángulo, determinar las restantes La geometría (teórica) nos dice cuándo ciertos datos determinan que salvo por posición un triángulo de lados dados, la trigonometría (práctica) nos dice cómo calcular los restantes.

Comencemos con triángulos rectángulos. Si conocemos de los lados del triángulo, como el Teorema de Pitágoras afirma que c b a a 2 + b 2 = c 2, conocemos el tercer lado. Eso sí, debemos saber si los lados que conocemos son catetos o la hipotenusa.

Resolución de triángulos rectángulos. Pero no tenemos ninguna información acerca de los ángulos. A continuación comenzaremos a abordar este problema. Dividimos los catetos en r partes iguales, y formamos una retícula. Los catetos de los triángulos de las esquinas miden a/r, b/r y su hipotenusa será, por el Teorema de Pitágoras igual a c/r. NOTEMOS que la hipotenusa pasa por los puntos de la retícula. Los triángulo de las esquinas tienen los mismos ángulos.

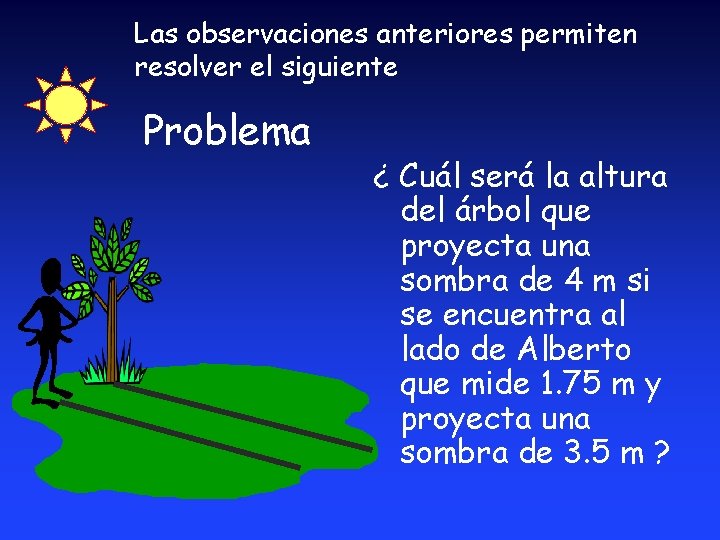
Las observaciones anteriores permiten resolver el siguiente Problema ¿ Cuál será la altura del árbol que proyecta una sombra de 4 m si se encuentra al lado de Alberto que mide 1. 75 m y proyecta una sombra de 3. 5 m ?

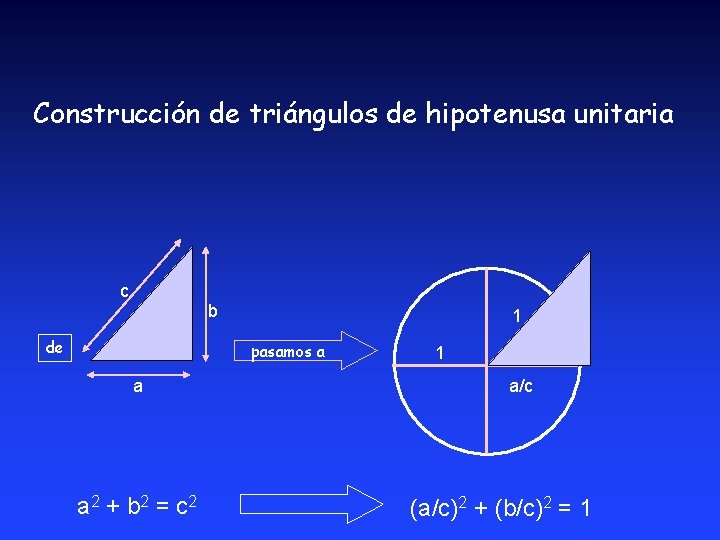
Sigamos con el problema de encontrar los ángulos en triángulos rectángulos. Vamos a escoger triángulos “normalizados”, que representen a cada triángulo rectángulo. Tomaremos triángulos con hipotenusa unitaria.

Construcción de triángulos de hipotenusa unitaria c b de 1 pasamos a a a 2 + b 2 = c 2 b/c 1 a/c (a/c)2 + (b/c)2 = 1

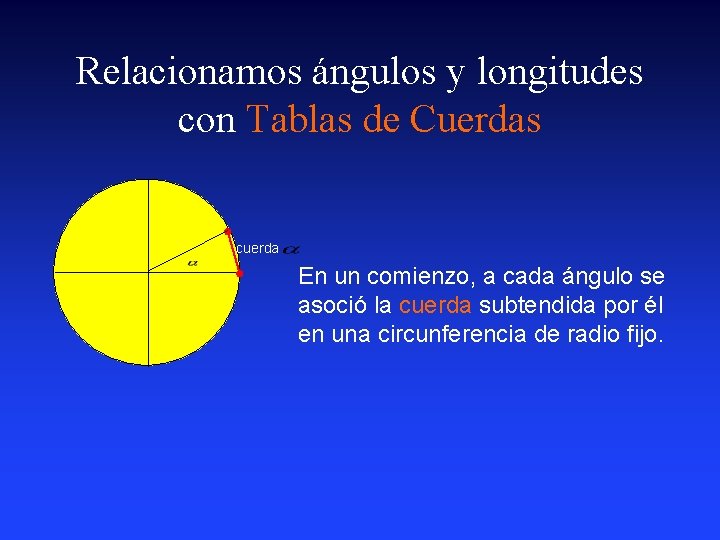
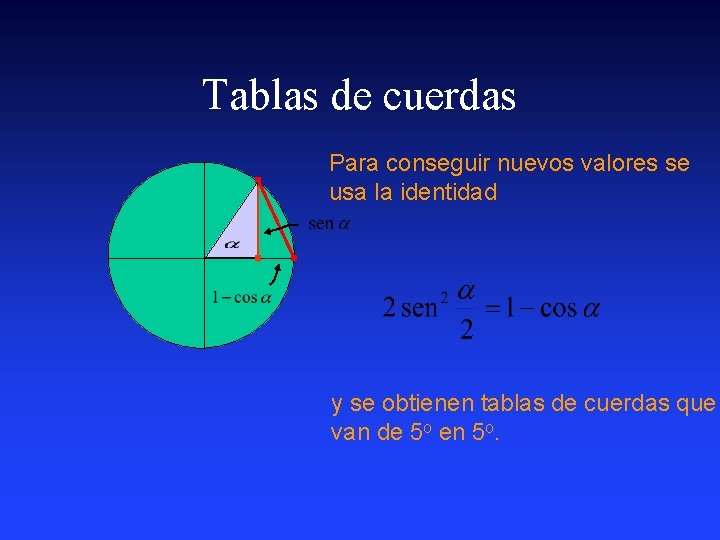
Relacionamos ángulos y longitudes con Tablas de Cuerdas cuerda En un comienzo, a cada ángulo se asoció la cuerda subtendida por él en una circunferencia de radio fijo.

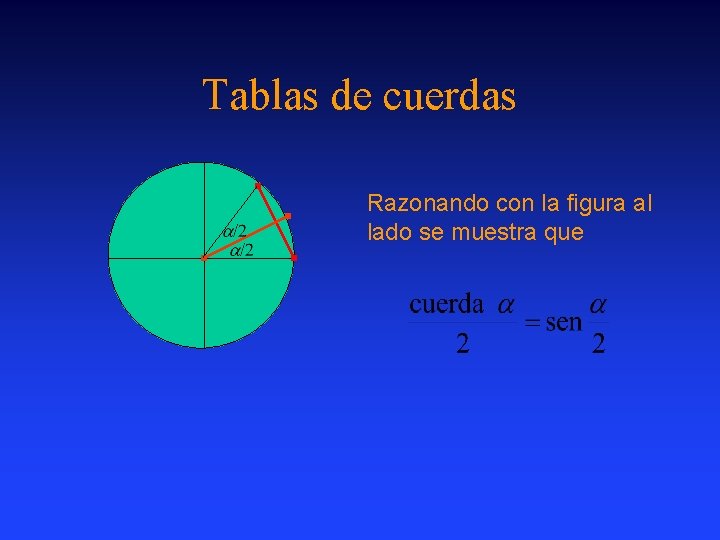
Tablas de cuerdas Razonando con la figura al lado se muestra que

Tablas de cuerdas Para conseguir nuevos valores se usa la identidad y se obtienen tablas de cuerdas que van de 5 o en 5 o.

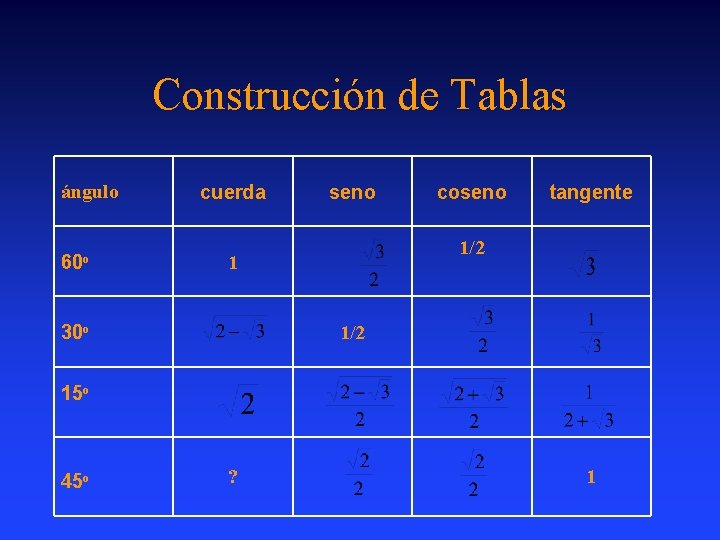
Construcción de Tablas ángulo 60 o cuerda seno tangente 1/2 1 30 o coseno 1/2 15 o 45 o ? 1

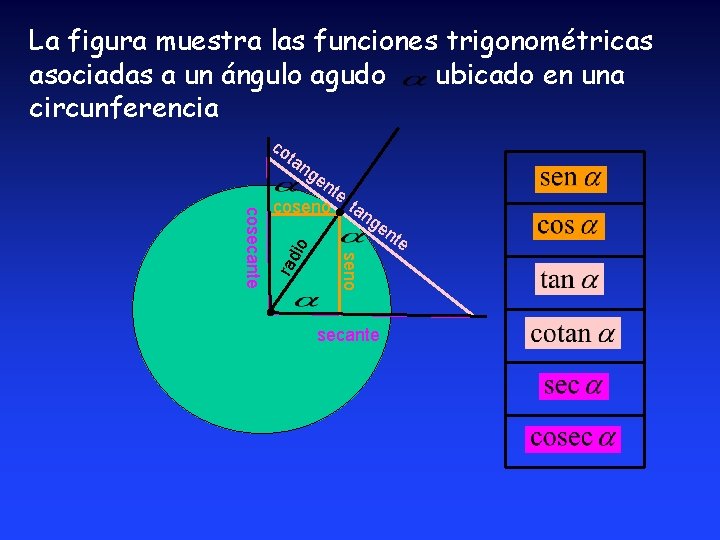
La figura muestra las funciones trigonométricas asociadas a un ángulo agudo ubicado en una circunferencia co ta ng en io rad seno cosecante te coseno tan ge nt e secante

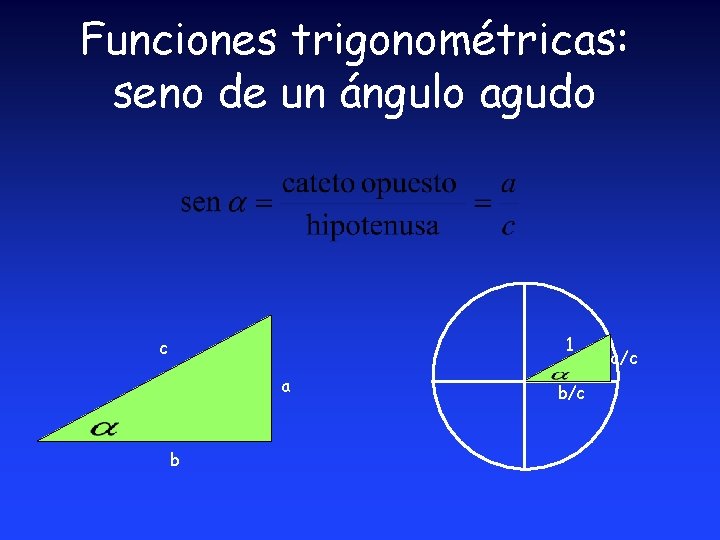
Funciones trigonométricas: seno de un ángulo agudo 1 c a b b/c a/c

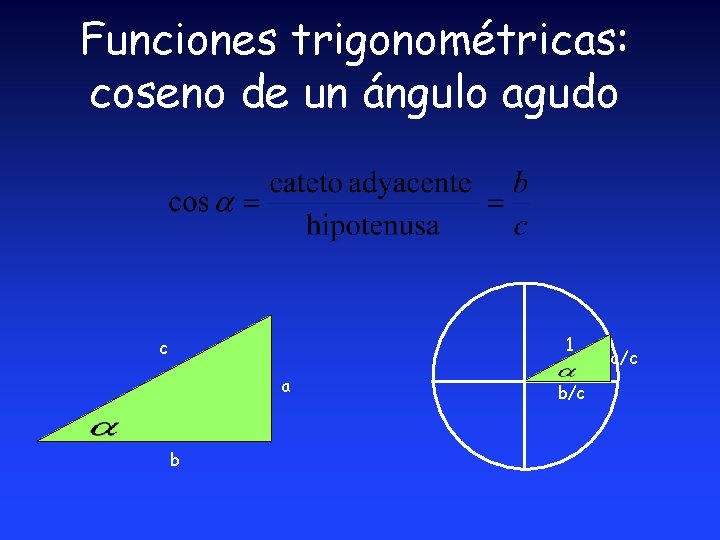
Funciones trigonométricas: coseno de un ángulo agudo 1 c a b b/c a/c

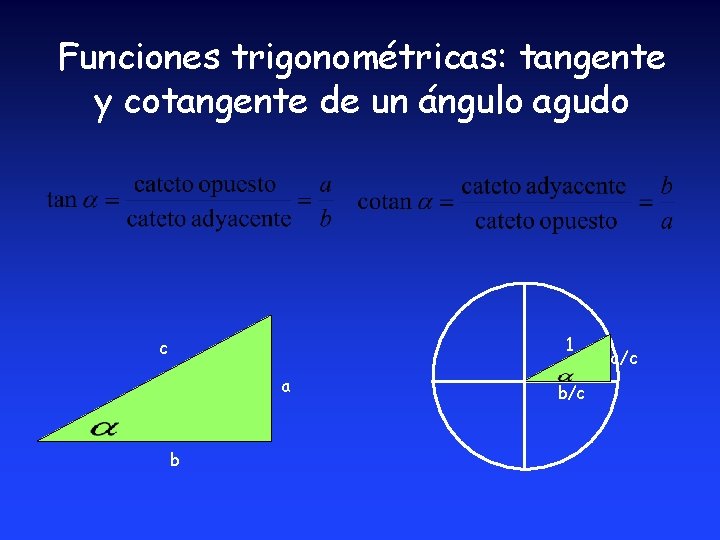
Funciones trigonométricas: tangente y cotangente de un ángulo agudo 1 c a b b/c a/c

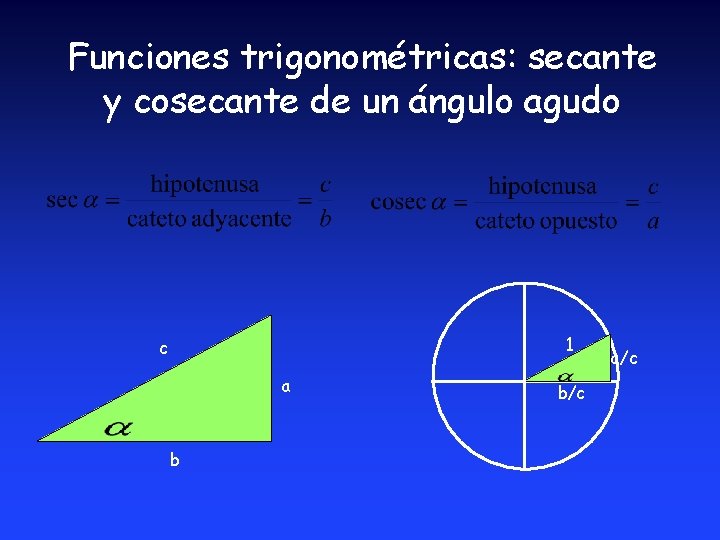
Funciones trigonométricas: secante y cosecante de un ángulo agudo 1 c a b b/c a/c

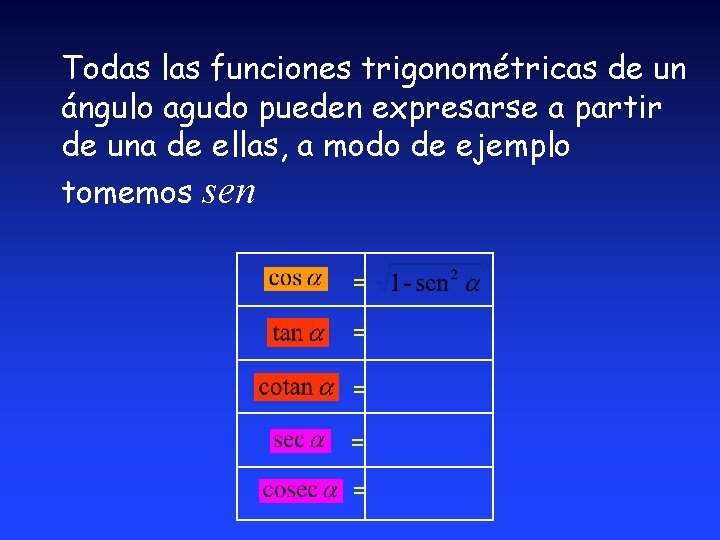
Todas las funciones trigonométricas de un ángulo agudo pueden expresarse a partir de una de ellas, a modo de ejemplo tomemos sen = = =

Identidades Trigonométricas 1 cos sen La identidad fundamental es consecuencia del Teorema de Pitágoras

Identidades Trigonométricas 1 sen cos Si es el ángulo complementario de , hay un triángulo rectángulo que los tiene como ángulos agudos y se tiene que

Identidades Trigonométricas En una diapositiva anterior demostramos que 1 o bien, tomando

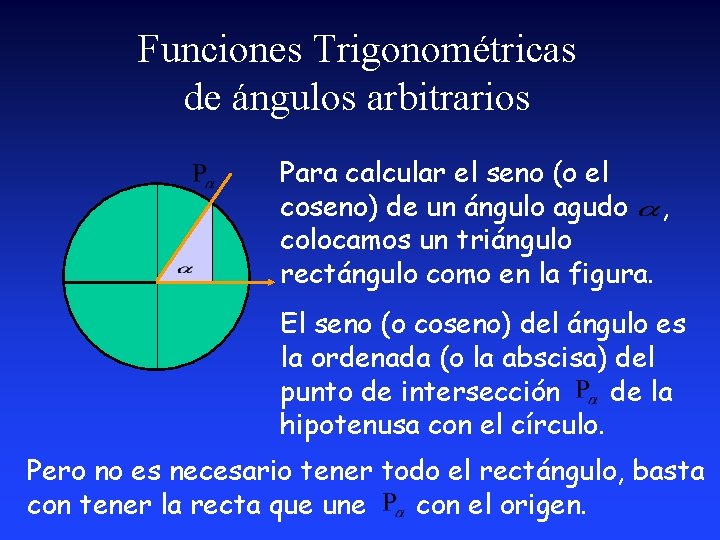
Funciones Trigonométricas de ángulos arbitrarios Para calcular el seno (o el coseno) de un ángulo agudo , colocamos un triángulo rectángulo como en la figura. El seno (o coseno) del ángulo es la ordenada (o la abscisa) del punto de intersección de la hipotenusa con el círculo. Pero no es necesario tener todo el rectángulo, basta con tener la recta que une con el origen.

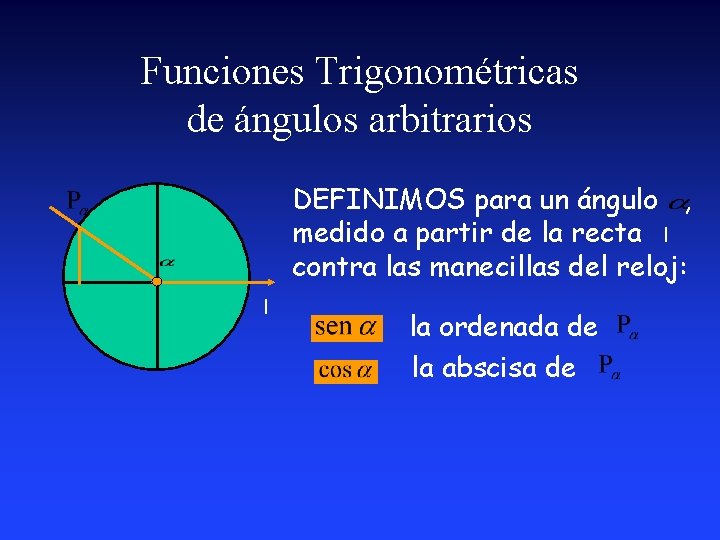
Funciones Trigonométricas de ángulos arbitrarios DEFINIMOS para un ángulo , medido a partir de la recta l contra las manecillas del reloj: l la ordenada de la abscisa de

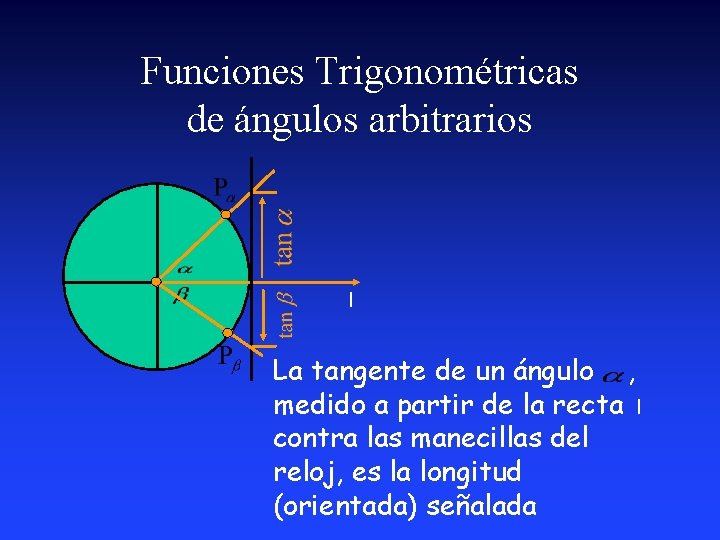
Funciones Trigonométricas de ángulos arbitrarios l La tangente de un ángulo , medido a partir de la recta l contra las manecillas del reloj, es la longitud (orientada) señalada

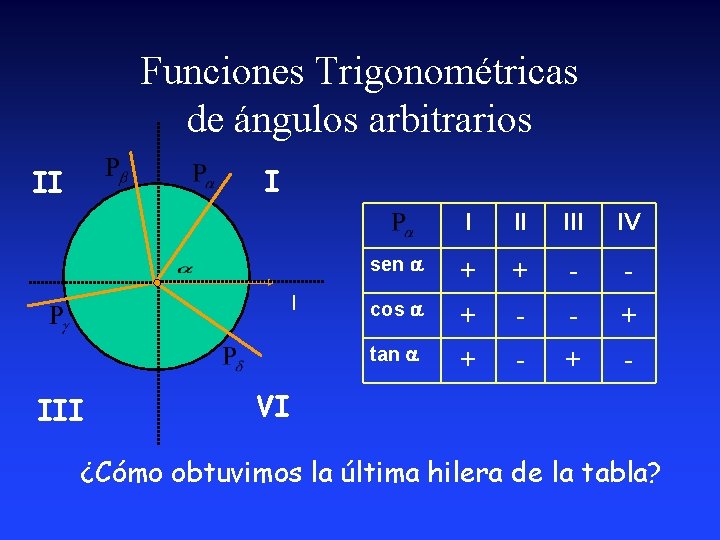
Funciones Trigonométricas de ángulos arbitrarios I II l III IV sen a + + - - cos a + - - + tan a + - VI ¿Cómo obtuvimos la última hilera de la tabla?

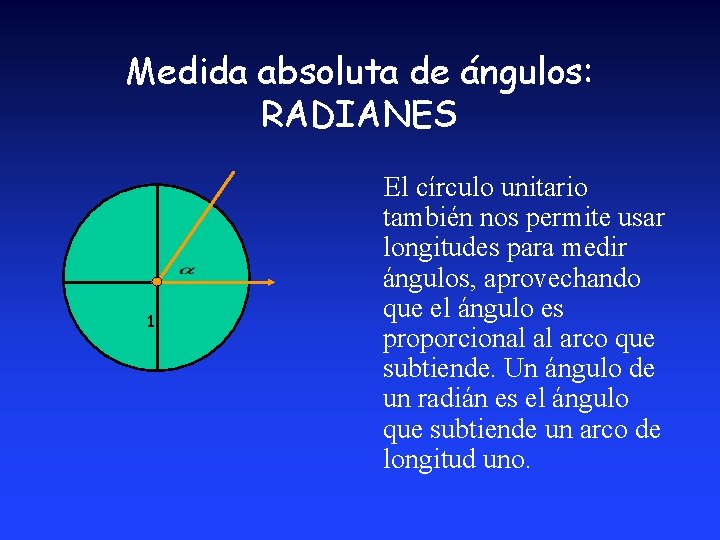
Medida absoluta de ángulos: RADIANES 1 El círculo unitario también nos permite usar longitudes para medir ángulos, aprovechando que el ángulo es proporcional al arco que subtiende. Un ángulo de un radián es el ángulo que subtiende un arco de longitud uno.

Medida absoluta de ángulos: RADIANES Como la circunferencia unitaria mide 2 , un cuarto de circunferencia mide /2 y como un ángulo recto subtiende un cuarto de circunferencia, el ángulo recto mide /2 radianes.

Medida absoluta de ángulos: RADIANES Como /2 90 o Entonces si Rad es la medida de un ángulo en radianes y Grad la medida en grados,

Medida absoluta de ángulos: RADIANES ángulo en radianes ángulo en grados 1 1 /3 45 120

Actividad I… Construir un triángulo cuyos lados sean de longitud 3, 4 y 5. Comparar los distintos triángulos que se obtienen. Nota: cada quien es libre de escoger la escala

…Actividad I Con la escala proporcionada, medir la razón entre pares de lados del triángulo diseñado Medir en centímetros lados del triángulo diseñado y obtenga la razón entre los pares de lados

Actividad II… Para cada uno de los triángulos rectángulos proporcionados, midan las siguientes razones, según el ángulo marcado con el círculo rojo: a) Cateto opuesto e hipotenusa b) Cateto adyacente e hipotenusa c) Cateto opuesto y cateto adyacente

… Actividad II

Problema 5 O En una circunferencia de centro O y radio 5 está trazada una cuerda que mide 3. 5 ¿cuánto mide el ángulo central asociado? En la misma circunferencia, halle la longitud de la cuerda subtendida por un ángulo de 72 o.

Problema 101 m C 100 m Una cuerda de 100 m de largo se estira un metro más y se sostiene del centro (ver la figura). ¿ A qué altura se encuentra el punto C? Dé una medida aproximada del ángulo.

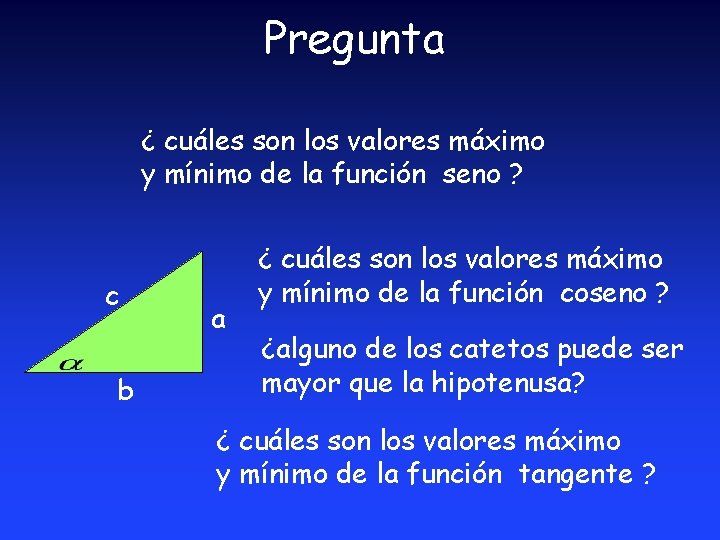
Pregunta ¿ cuáles son los valores máximo y mínimo de la función seno ? c b a ¿ cuáles son los valores máximo y mínimo de la función coseno ? ¿alguno de los catetos puede ser mayor que la hipotenusa? ¿ cuáles son los valores máximo y mínimo de la función tangente ?

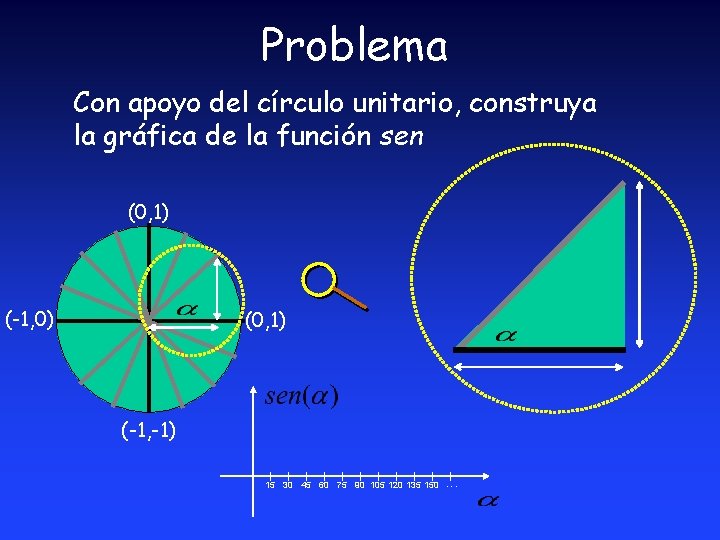
Problema Con apoyo del círculo unitario, construya la gráfica de la función sen (0, 1) (-1, 0) (0, 1) (-1, -1) 15 30 45 60 75 90 105 120 135 150 ···

Problema… 1. Trace los triángulos rectángulos definidos por las siguientes ternas de puntos: a) (0, 0), (8, 6) b) (0, 0), (-4, 3) c) (0, 0), (-3, -4) d) (0, 0), (8, -6), (8, 0) 2. En cada uno de los triángulos trazados, ubique el ángulo formado entre la hipotenusa y el eje de las abscisas. 3. Calcule el seno, coseno y tangente de tal ángulo.

… Problema II I IV I II IV sen(a) + + - - cos(a) + - - + tan(a) + -