TRIGONOMETRA ETIMOLOGA Trigonometra viene de Trigonos tres ngulos

TRIGONOMETRÍA

ETIMOLOGÍA Trigonometría viene de Tri-gonos = tres ángulos = triángulo y de metros = medir Es decir, significa medida de ángulos DEFINICIÓN La Trigonometría es la rama de las matemáticas que estudia las relaciones entre los lados y los ángulos de los triángulos.

MEDIDAS DE ÁNGULOS: • SISTEMA SEXAGESIMAL • SISTEMA CENTESIMAL • RADIANES

• SISTEMA SEXAGESIMAL La circunferencia se divide en 360 partes iguales. Cada una de ellas es un grado sexagesimal. Cada grado se divide en 60 minutos y cada minuto en 60 segundos. En la calculadora aparece con la denominación DEG Notación: 30 grados, 40 minutos y 15 segundos = 30º 40’ 15’’

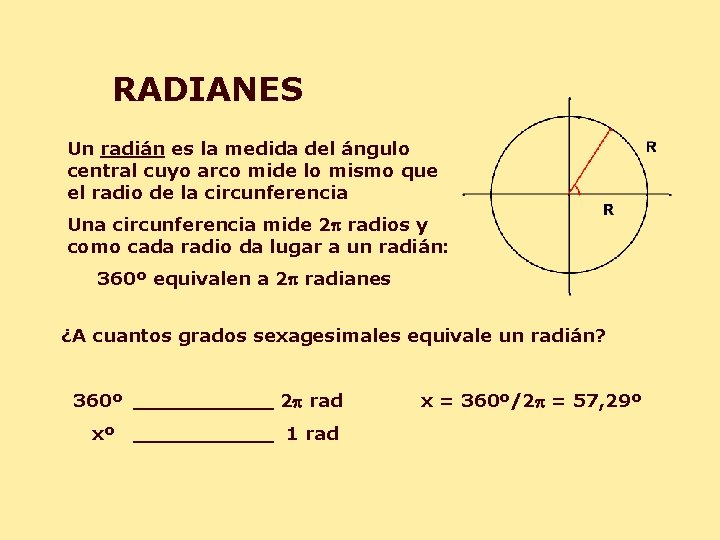
RADIANES Un radián es la medida del ángulo central cuyo arco mide lo mismo que el radio de la circunferencia Una circunferencia mide 2 p radios y como cada radio da lugar a un radián: 360º equivalen a 2 p radianes ¿A cuantos grados sexagesimales equivale un radián? 360º ______ 2 p rad xº ______ 1 rad x = 360º/2 p = 57, 29º

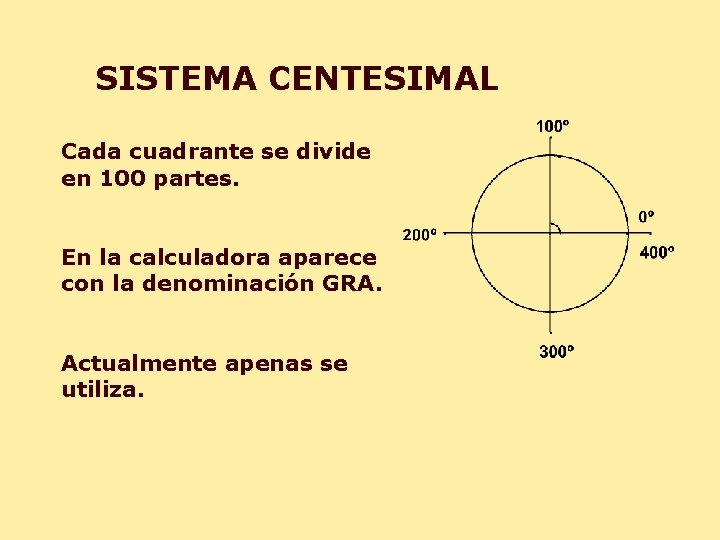
SISTEMA CENTESIMAL Cada cuadrante se divide en 100 partes. En la calculadora aparece con la denominación GRA. Actualmente apenas se utiliza.

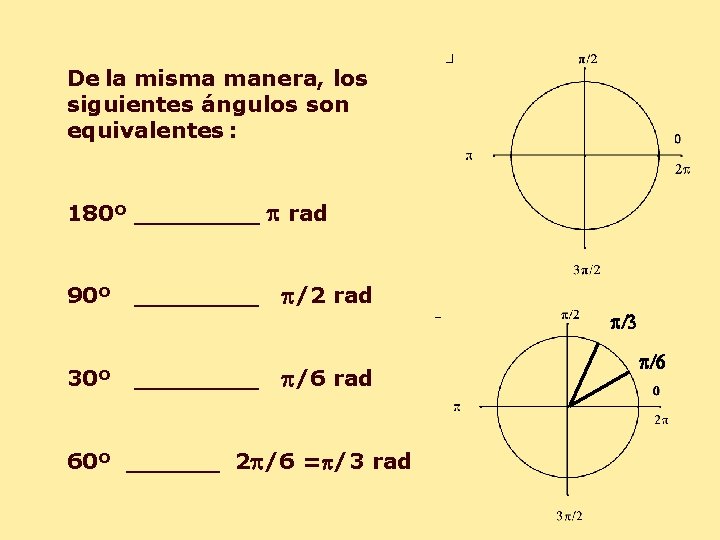
De la misma manera, los siguientes ángulos son equivalentes : 180º ____ p rad 90º ____ p/2 rad p/3 30º ____ p/6 rad 60º ______ 2 p/6 =p/3 rad p/6

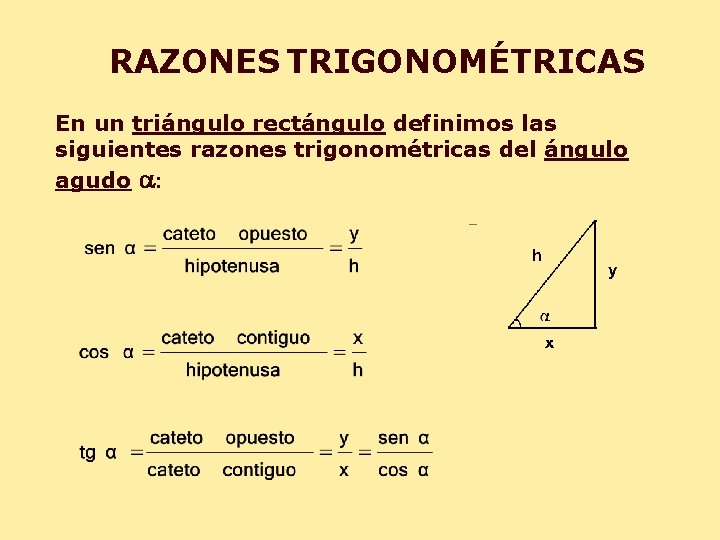
RAZONES TRIGONOMÉTRICAS En un triángulo rectángulo definimos las siguientes razones trigonométricas del ángulo agudo a:

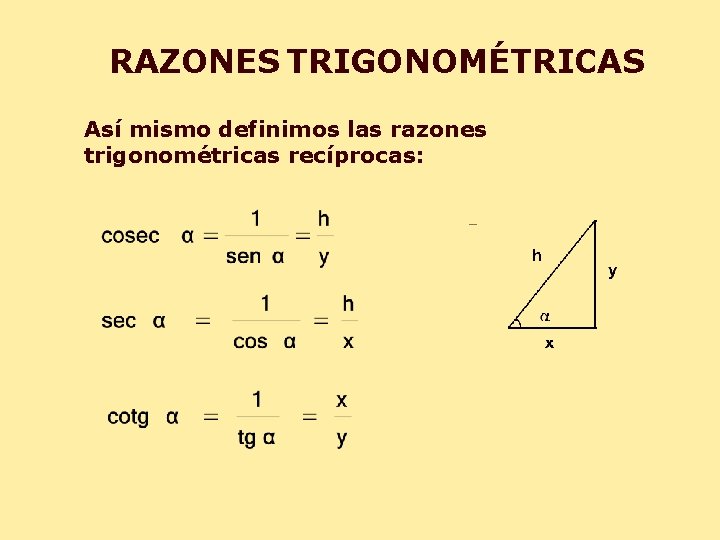
RAZONES TRIGONOMÉTRICAS Así mismo definimos las razones trigonométricas recíprocas:

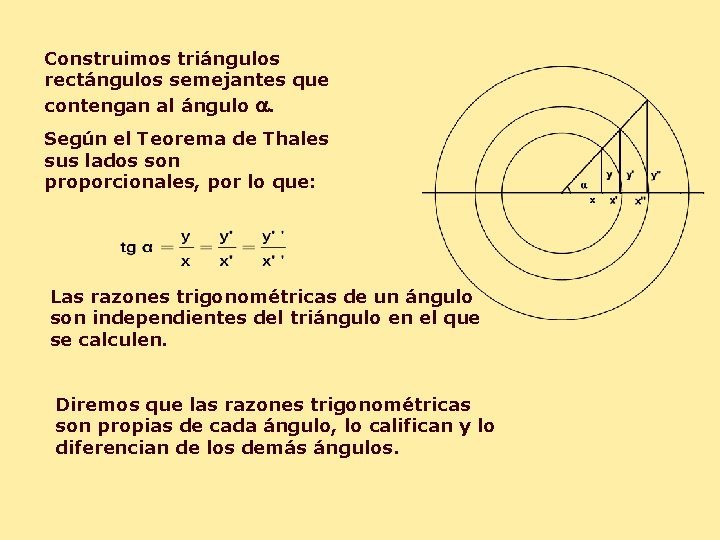
Construimos triángulos rectángulos semejantes que contengan al ángulo a. Según el Teorema de Thales sus lados son proporcionales, por lo que: Las razones trigonométricas de un ángulo son independientes del triángulo en el que se calculen. Diremos que las razones trigonométricas son propias de cada ángulo, lo califican y lo diferencian de los demás ángulos.

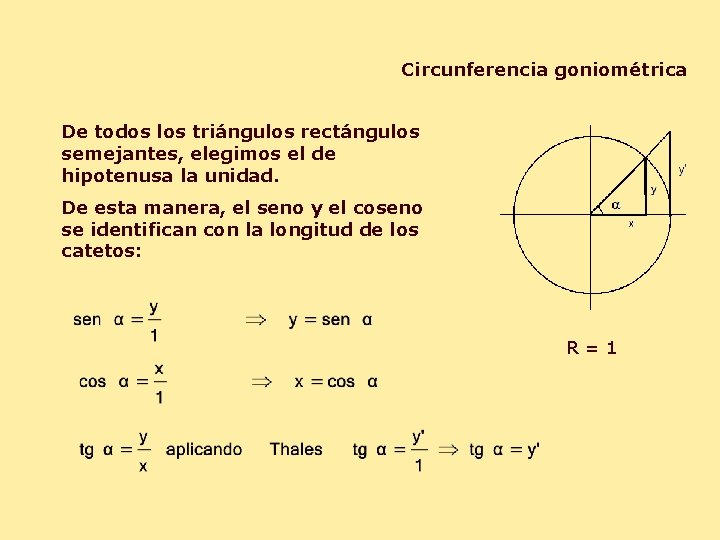
Circunferencia goniométrica De todos los triángulos rectángulos semejantes, elegimos el de hipotenusa la unidad. De esta manera, el seno y el coseno se identifican con la longitud de los catetos: R=1

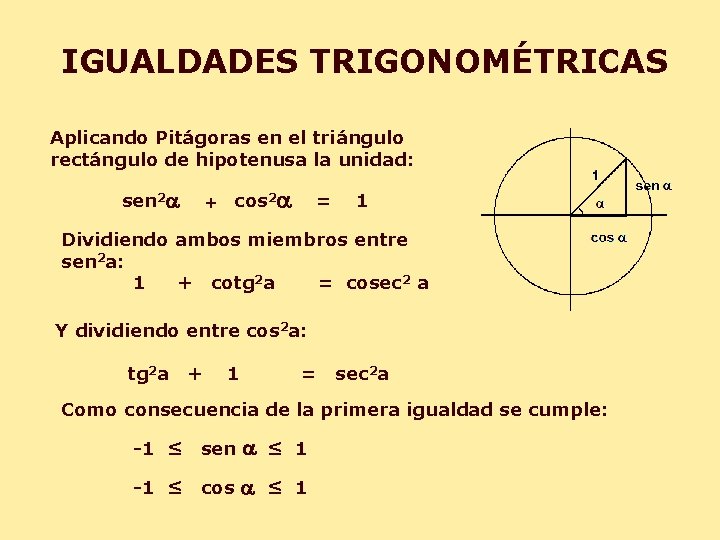
IGUALDADES TRIGONOMÉTRICAS Aplicando Pitágoras en el triángulo rectángulo de hipotenusa la unidad: sen 2 a cos 2 a + = 1 Dividiendo ambos miembros entre sen 2 a: 1 + cotg 2 a = cosec 2 a Y dividiendo entre cos 2 a: tg 2 a + 1 = sec 2 a Como consecuencia de la primera igualdad se cumple: -1 ≤ sen a ≤ 1 -1 ≤ cos a ≤ 1

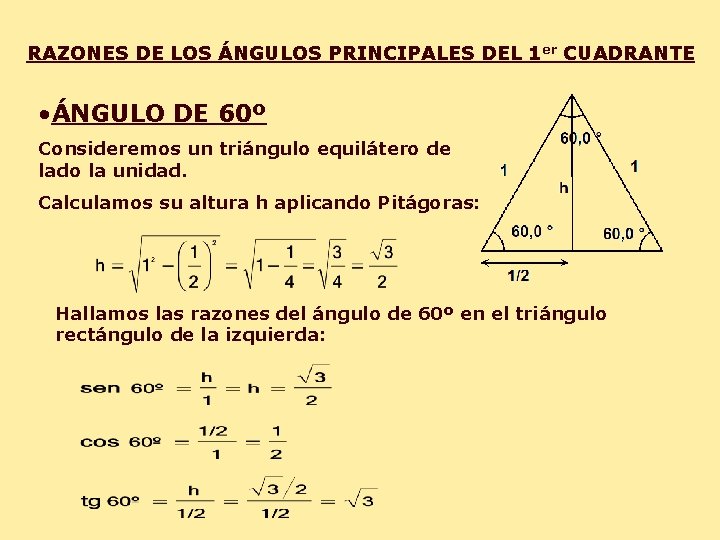
RAZONES DE LOS ÁNGULOS PRINCIPALES DEL 1 er CUADRANTE • ÁNGULO DE 60º Consideremos un triángulo equilátero de lado la unidad. Calculamos su altura h aplicando Pitágoras: Hallamos las razones del ángulo de 60º en el triángulo rectángulo de la izquierda:

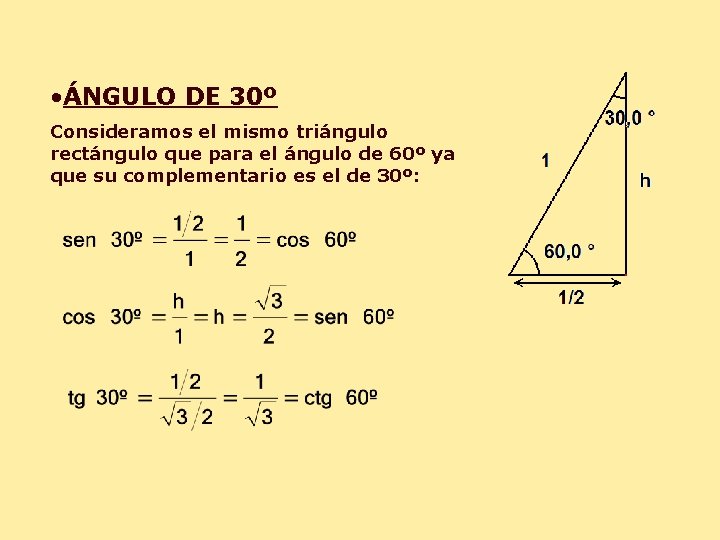
• ÁNGULO DE 30º Consideramos el mismo triángulo rectángulo que para el ángulo de 60º ya que su complementario es el de 30º:

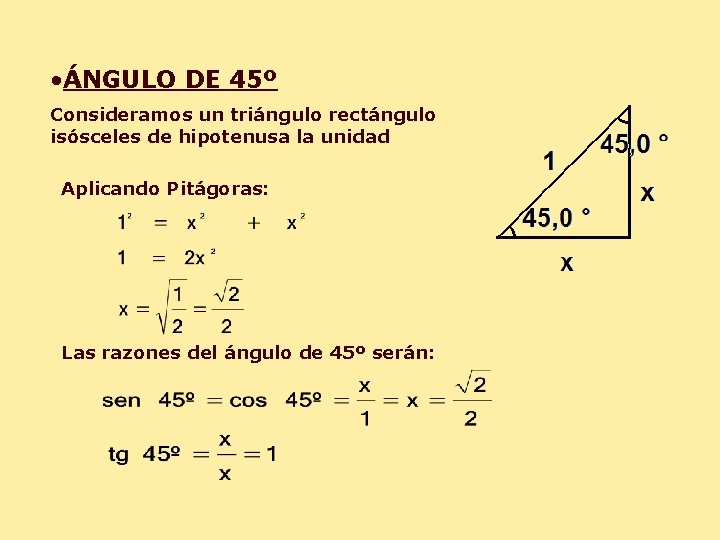
• ÁNGULO DE 45º Consideramos un triángulo rectángulo isósceles de hipotenusa la unidad Aplicando Pitágoras: Las razones del ángulo de 45º serán:

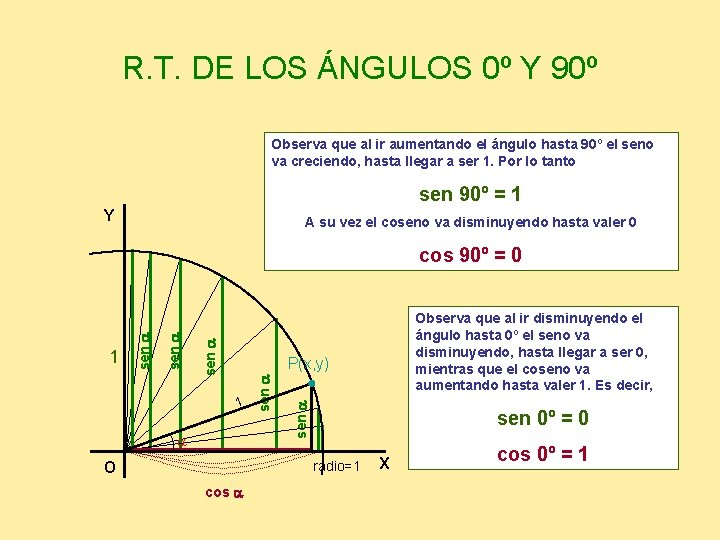
R. T. DE LOS ÁNGULOS 0º Y 90º Observa que al ir aumentando el ángulo hasta 90º el seno va creciendo, hasta llegar a ser 1. Por lo tanto sen 90º = 1 Y A su vez el coseno va disminuyendo hasta valer 0 sen a Observa que al ir disminuyendo el ángulo hasta 0º el seno va disminuyendo, hasta llegar a ser 0, mientras que el coseno va aumentando hasta valer 1. Es decir, 1 a sen a P(x, y) sen a 1 sen a cos 90º = 0 sen 0º = 0 radio=1 O cos a X cos 0º = 1

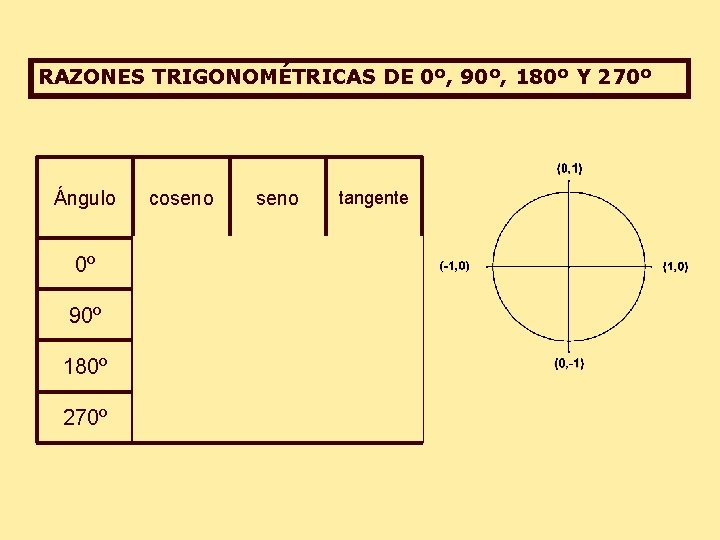
RAZONES TRIGONOMÉTRICAS DE 0º, 90º, 180º Y 270º Ángulo coseno tangente 0º 1 0 0 90º 0 1 ∞ 180º -1 0 0 270º 0 -1 ∞

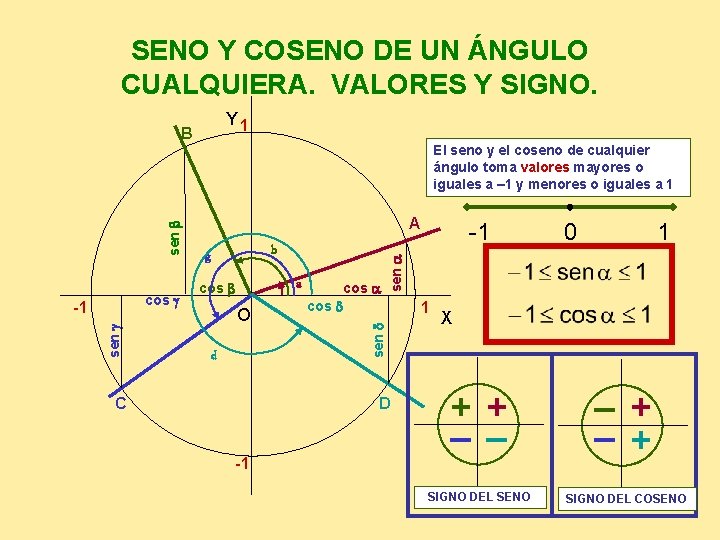
SENO Y COSENO DE UN ÁNGULO CUALQUIERA. VALORES Y SIGNO. Y 1 B sen g -1 b g a cos b O d C cos a -1 0 1 sen a cos g A cos d 1 sen d sen b El seno y el coseno de cualquier ángulo toma valores mayores o iguales a – 1 y menores o iguales a 1 D X + _ _ + SIGNO DEL SENO SIGNO DEL COSENO -1

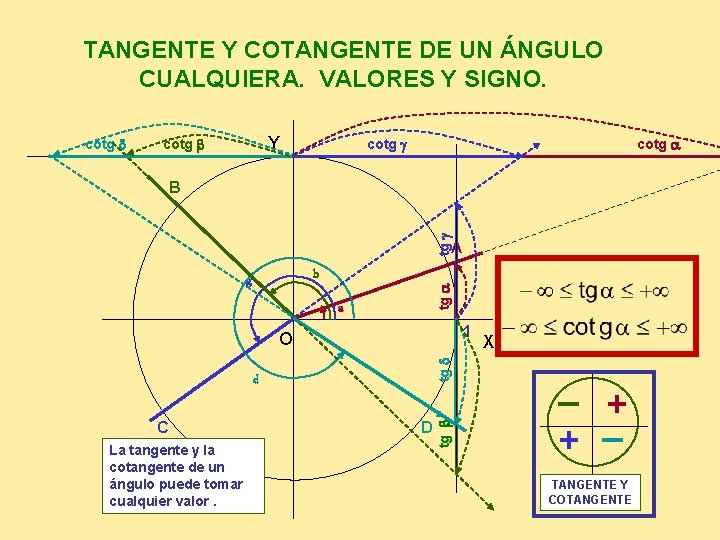
TANGENTE Y COTANGENTE DE UN ÁNGULO CUALQUIERA. VALORES Y SIGNO. cotg d Y cotg b cotg g cotg a tg g B A tg a b g a 1 d C La tangente y la cotangente de un ángulo puede tomar cualquier valor. D tg b tg d O X _ + TANGENTE Y COTANGENTE

REDUCCIÓN DE ÁNGULOS AL 1 er CUADRANTE a) ÁNGULOS COMPLEMENTARIOS a + b = 90º - a sen a = cos ( 90º - a ) cos a = sen ( 90º - a ) tg a = ctg ( 90º - a )

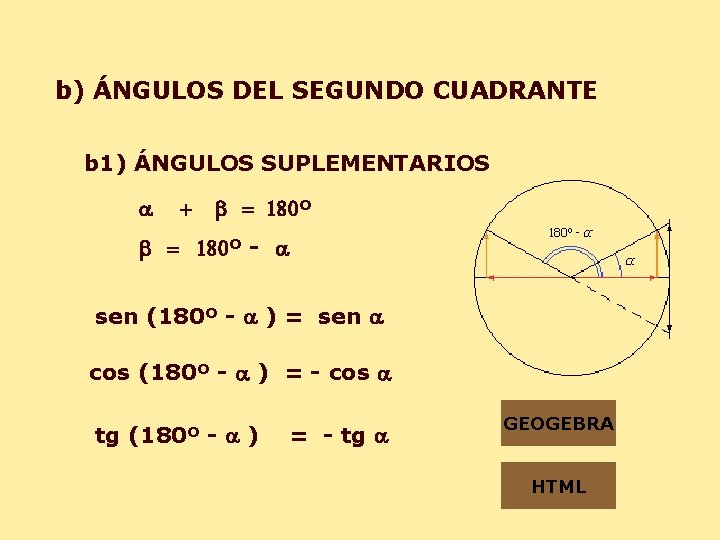
b) ÁNGULOS DEL SEGUNDO CUADRANTE b 1) ÁNGULOS SUPLEMENTARIOS a + b = 180º - a sen (180º - a ) = sen a cos (180º - a ) = - cos a tg (180º - a ) = - tg a GEOGEBRA HTML

b 2) ÁNGULOS a y p/2 + a sen ( p/2 + a ) = cos a cos ( p/2 + a ) = - sen a tg ( p/2 + a ) = - cotg a

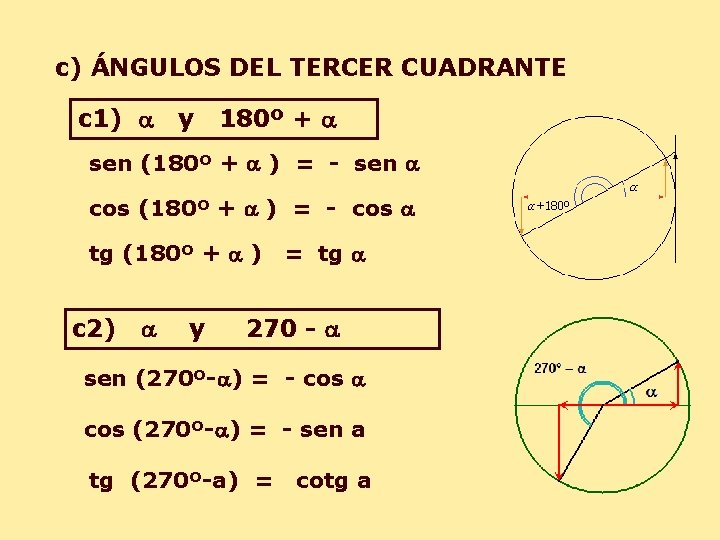
c) ÁNGULOS DEL TERCER CUADRANTE c 1) a y 180º + a sen (180º + a ) = - sen a cos (180º + a ) = - cos a tg (180º + a ) c 2) a y = tg a 270 - a sen (270º-a) = - cos a cos (270º-a) = - sen a tg (270º-a) = cotg a

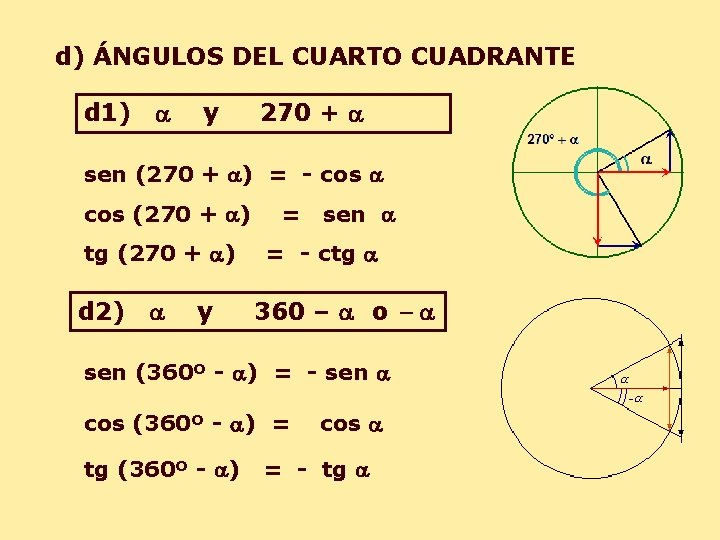
d) ÁNGULOS DEL CUARTO CUADRANTE d 1) a y 270 + a sen (270 + a) = - cos a cos (270 + a) tg (270 + a) d 2) a y = sen a = - ctg a 360 – a o - a sen (360º - a) = - sen a cos (360º - a) = tg (360º - a) cos a = - tg a

FUNCIONES TRIGONOMÉTRICAS 1. FUNCIÓN SENO 2. FUNCIÓN COSENO 3. FUNCIÓN TANGENTE

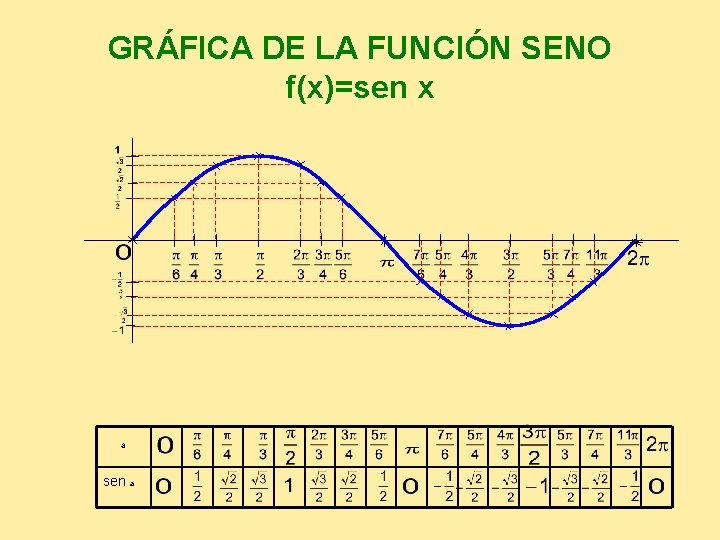
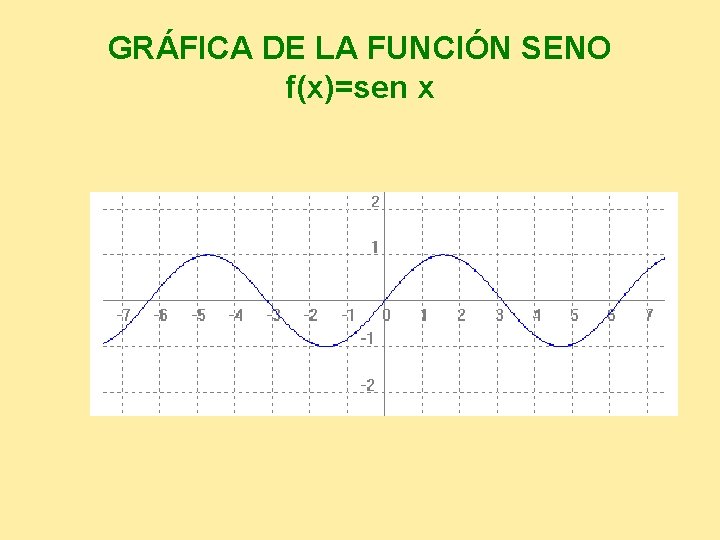
GRÁFICA DE LA FUNCIÓN SENO f(x)=sen x a sen a

GRÁFICA DE LA FUNCIÓN SENO f(x)=sen x

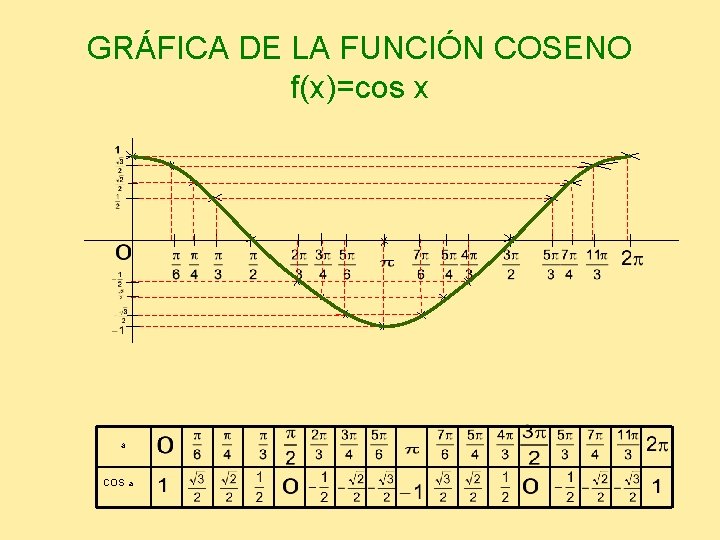
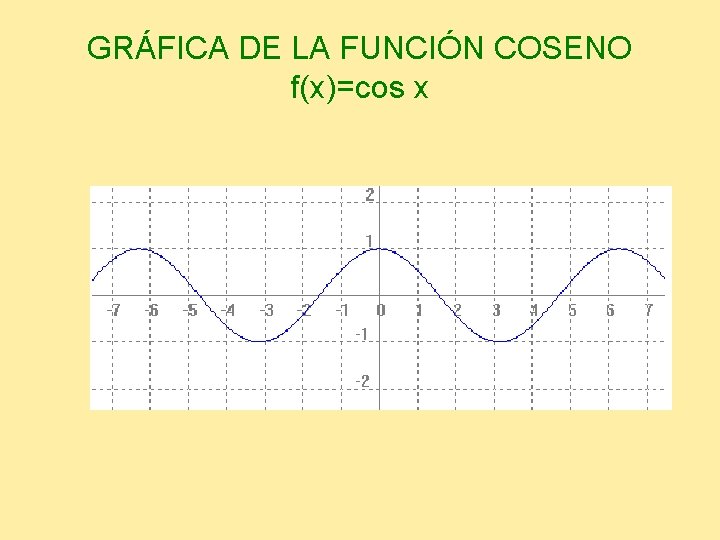
GRÁFICA DE LA FUNCIÓN COSENO f(x)=cos x a COS a

GRÁFICA DE LA FUNCIÓN COSENO f(x)=cos x

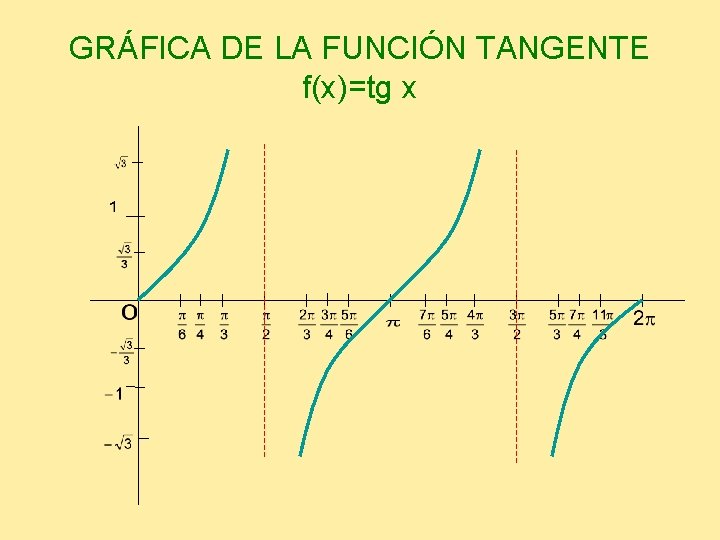
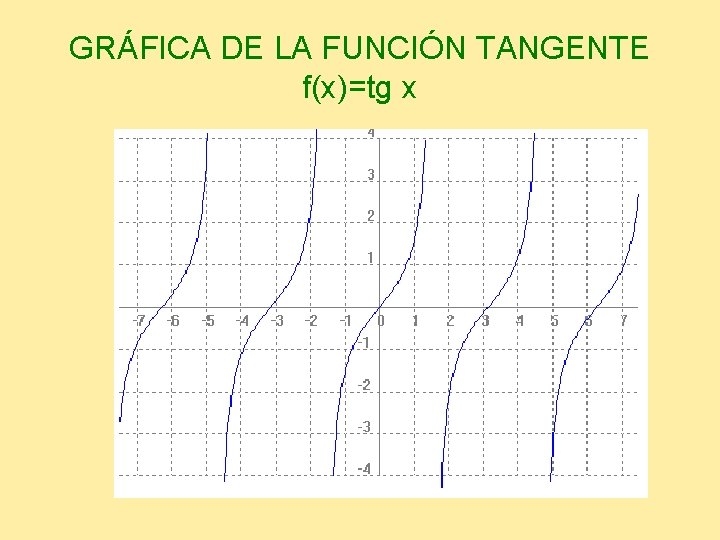
GRÁFICA DE LA FUNCIÓN TANGENTE f(x)=tg x

GRÁFICA DE LA FUNCIÓN TANGENTE f(x)=tg x

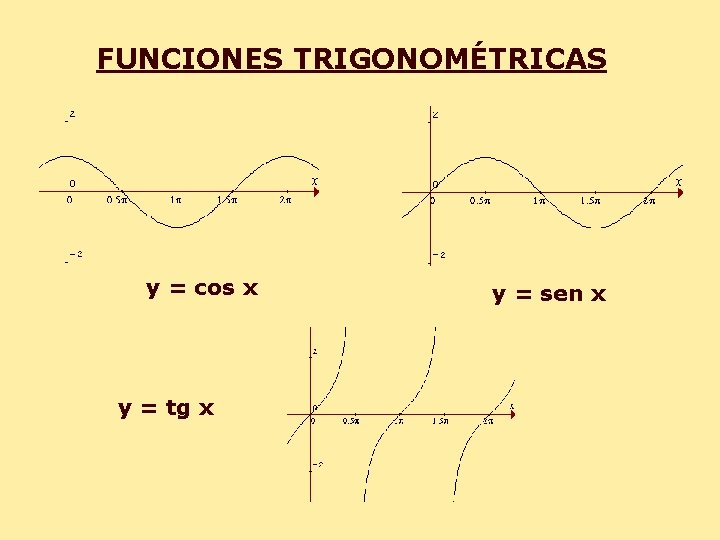
FUNCIONES TRIGONOMÉTRICAS y = cos x y = tg x y = sen x