Trigonometra y ngulos sin Razones Trigonomtricas de ngulos

Trigonometría y ángulos

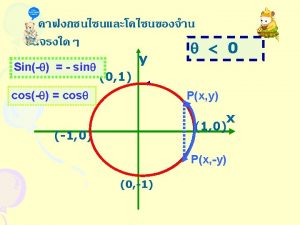
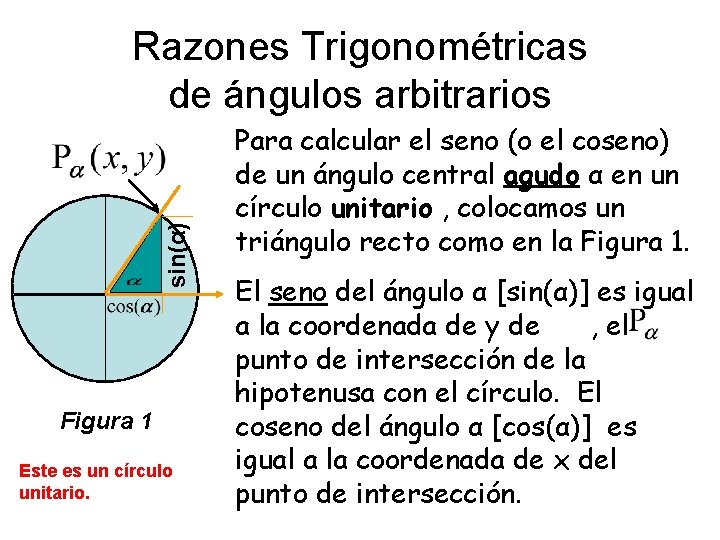
sin(α) Razones Trigonométricas de ángulos arbitrarios Figura 1 Este es un círculo unitario. Para calcular el seno (o el coseno) de un ángulo central agudo α en un círculo unitario , colocamos un triángulo recto como en la Figura 1. El seno del ángulo α [sin(α)] es igual a la coordenada de y de , el punto de intersección de la hipotenusa con el círculo. El coseno del ángulo α [cos(α)] es igual a la coordenada de x del punto de intersección.

Razones Trigonométricas de ángulos arbitrarios y Figura 2 Este es un círculo unitario. En la Figura 2, el lado terminal del ángulo α está en el cuadrante II. El ángulo α NO es agudo. Si construimos un triángulo recto, el segmento que va desde el centro l hasta el punto es la hipotenusa. Notamos que la coordenada de x del punto es negativa y la coordenada en y es positiva. Ell ángulo de la base del triángulo recto, ya no es α, ahora es (180 - α).

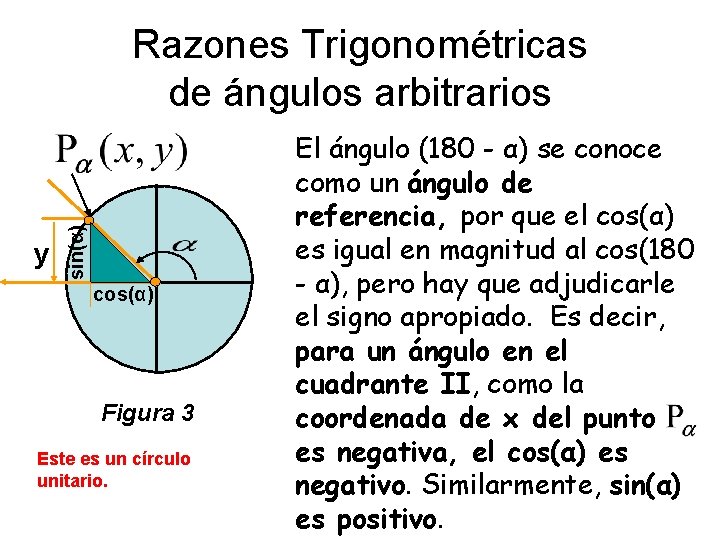
y sin(α) Razones Trigonométricas de ángulos arbitrarios cos(α) Figura 3 Este es un círculo unitario. El ángulo (180 - α) se conoce como un ángulo de referencia, por que el cos(α) es igual en magnitud al cos(180 - α), pero hay que adjudicarle l el signo apropiado. Es decir, para un ángulo en el cuadrante II, como la l coordenada de x del punto es negativa, el cos(α) es negativo. Similarmente, sin(α) es positivo.

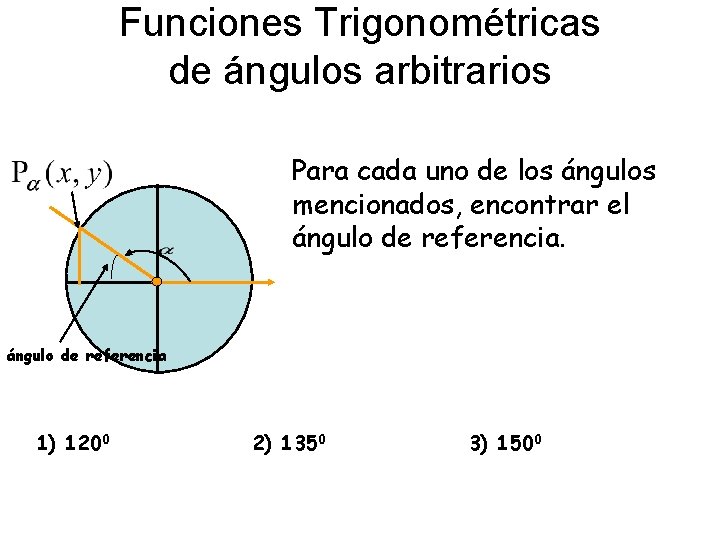
Funciones Trigonométricas de ángulos arbitrarios Para cada uno de los ángulos mencionados, encontrar el l ángulo de referencia 1) 1200 2) 1350 3) 1500

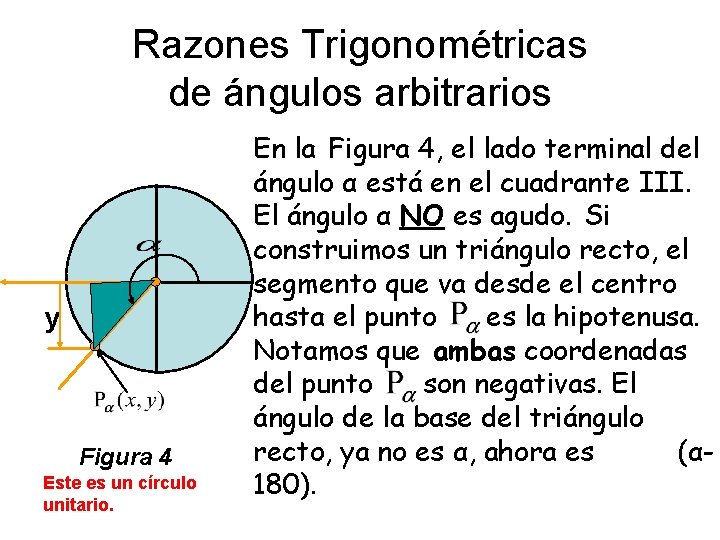
Razones Trigonométricas de ángulos arbitrarios y Figura 4 Este es un círculo unitario. En la Figura 4, el lado terminal del ángulo α está en el cuadrante III. El ángulo α NO es agudo. Si construimos un triángulo recto, el segmento que va desde el centro l hasta el punto es la hipotenusa. Notamos que ambas coordenadas del punto son negativas. El ángulo de la base del triángulol recto, ya no es α, ahora es (α 180).

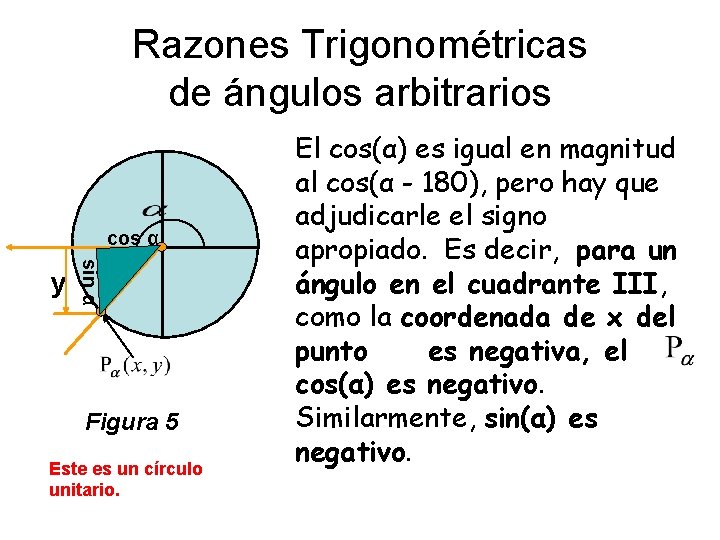
Razones Trigonométricas de ángulos arbitrarios cos α sin α y Figura 5 Este es un círculo unitario. El cos(α) es igual en magnitud al cos(α - 180), pero hay que adjudicarle el signo apropiado. Es decir, para un ángulo en el cuadrante III, como la coordenada de x del punto es negativa, el cos(α) es negativo. Similarmente, sin(α) es negativo.

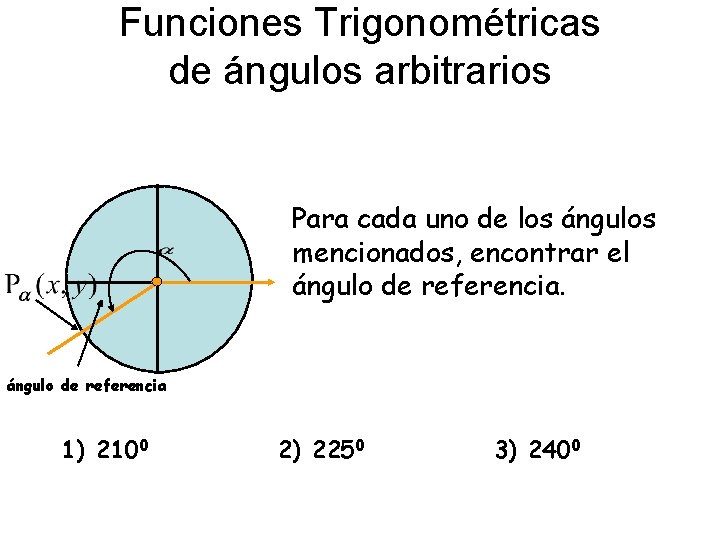
Funciones Trigonométricas de ángulos arbitrarios l Para cada uno de los ángulos l mencionados, encontrar el ángulo de referencia 1) 2100 2) 2250 3) 2400

Funciones Trigonométricas de ángulos arbitrarios y Figura 6 Este es un círculo unitario. En la Figura 6, el lado terminal del ángulo α está en el cuadrante IV. El ángulo α NO es agudo. Si construimos un triángulo recto, el segmento que va desde el centro hasta el punto es la hipotenusa. Notamos que la coordenada de x del punto es positiva y la coordenada de y es negativa. El ángulo de la base del triángulo recto, ya no es α, ahora es (360α).

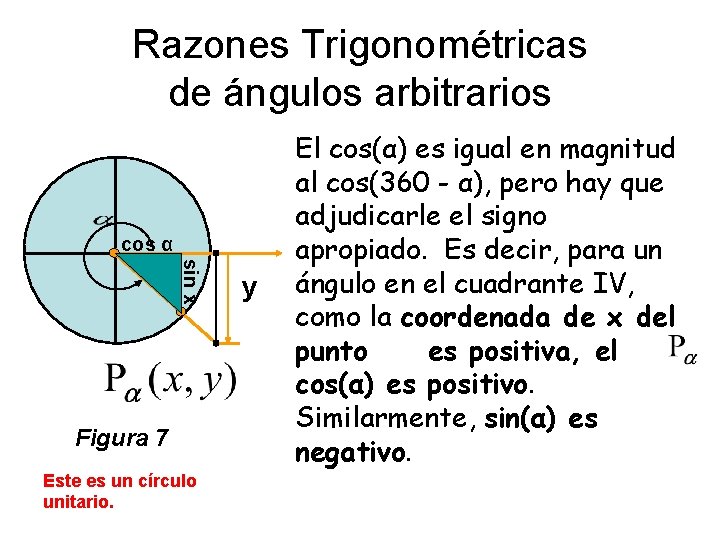
Razones Trigonométricas de ángulos arbitrarios cos α sin x Figura 7 Este es un círculo unitario. y El cos(α) es igual en magnitud al cos(360 - α), pero hay que adjudicarle el signo apropiado. Es decir, para un ángulo en el cuadrante IV, como la coordenada de x del punto es positiva, el cos(α) es positivo. Similarmente, sin(α) es negativo.

Funciones Trigonométricas de ángulos arbitrarios Para cada uno de los ángulos mencionados, encontrar el l ángulo de referencia. l 1) 3050 ángulo de referencia 2) 3150 3) 3300

Funciones Trigonométricas de ángulos arbitrarios Para un ángulo arbitrario α (no necesariamente agudo, no necesariamente en el cuadrante I, no necesariamente en un círculo unitario), medido a l partir del eje de x , en contra de las manecillas del reloj en un círculo unitario:

Funciones Trigonométricas de ángulos arbitrarios Para un ángulo arbitrario α (no necesariamente agudo, no necesariamente en el cuadrante I, no necesariamente en un círculo unitario), medido a partir del eje de x en contra de las manecillas dell reloj en un círculo unitario:

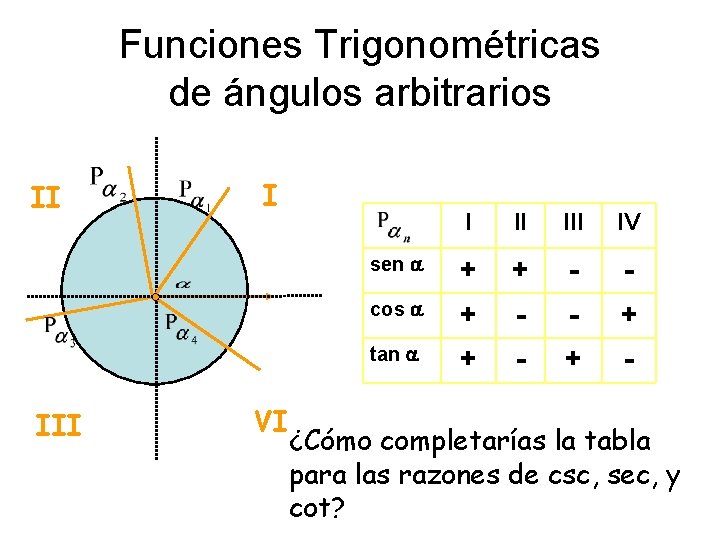
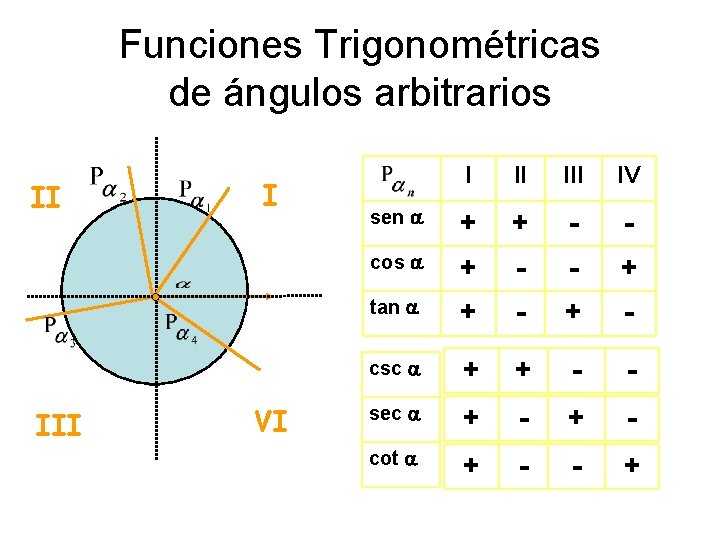
Funciones Trigonométricas de ángulos arbitrarios I II l III VI I II IV sen a + + - - cos a + - - + tan a + - ¿Cómo completarías la tabla ¿Cómo obtuvimospara la última hilera de de csc, la tabla? las razones sec, y cot?

Funciones Trigonométricas de ángulos arbitrarios II I l III VI I II IV sen a + + - - cos a + - - + tan a + - csc a + + - - sec a + - cot a + - - +

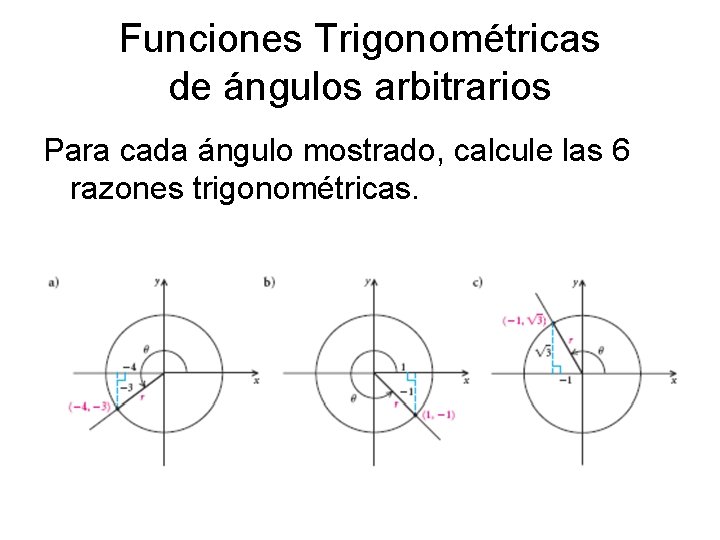
Funciones Trigonométricas de ángulos arbitrarios Para cada ángulo mostrado, calcule las 6 razones trigonométricas.

Funciones Trigonométricas de ángulos arbitrarios Este es un círculo unitario. Si un ángulo arbitrario α, se forma rotando un radio del círculo unitario (en contra del las manecillas del reloj) más de una rotación completa, entonces el ángulo medirá más de 3600. Encontrar el ángulo de referencia en estos casos requiere dos pasos:

Funciones Trigonométricas de ángulos arbitrarios Pasos: 1) eliminar las vueltas adicionales: medida del ángulo – l donde n es el número de vueltas al círculo. Este es un círculo unitario. [La nueva medida es la medida de un ángulo coterminal con el ángulo original. Angulos coterminales tienen el mismo lado terminal. )

Funciones Trigonométricas de ángulos arbitrarios Pasos: 2) determinar el ángulo de referencia dependiendo el l cuadrante en el cual cae la nueva medida según mostramos anteriormente. Este es un círculo unitario.

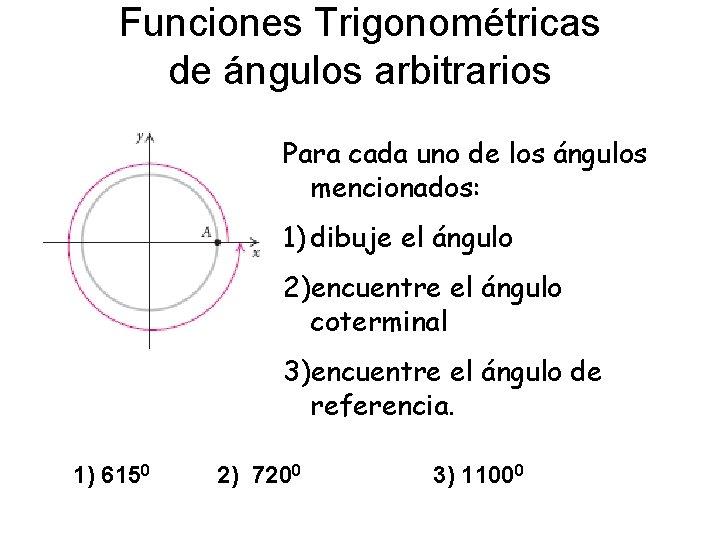
Funciones Trigonométricas de ángulos arbitrarios Para cada uno de los ángulos mencionados: 1) dibuje el ángulo 2)encuentre el ángulo coterminal 3)encuentre el ángulo de referencia. 1) 6150 2) 7200 3) 11000 l

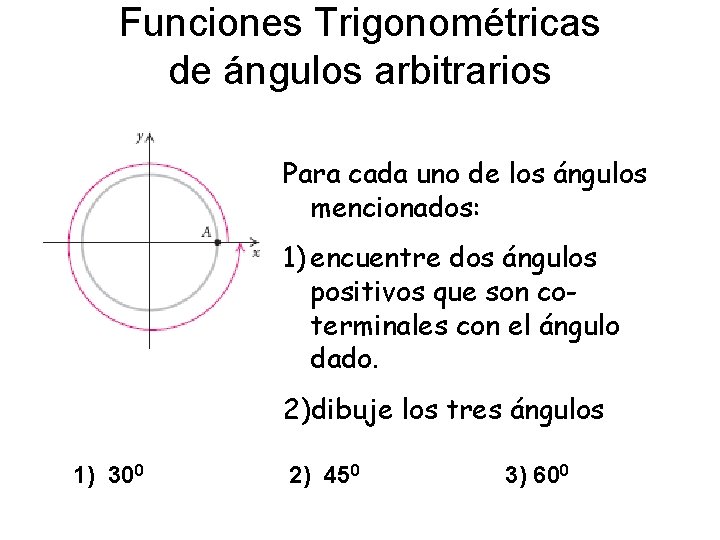
Funciones Trigonométricas de ángulos arbitrarios Para cada uno de los ángulos mencionados: 1) encuentre dos ángulos positivos que son coterminales con el ángulo dado. 2)dibuje los tres ángulos 1) 300 2) 450 3) 600 l

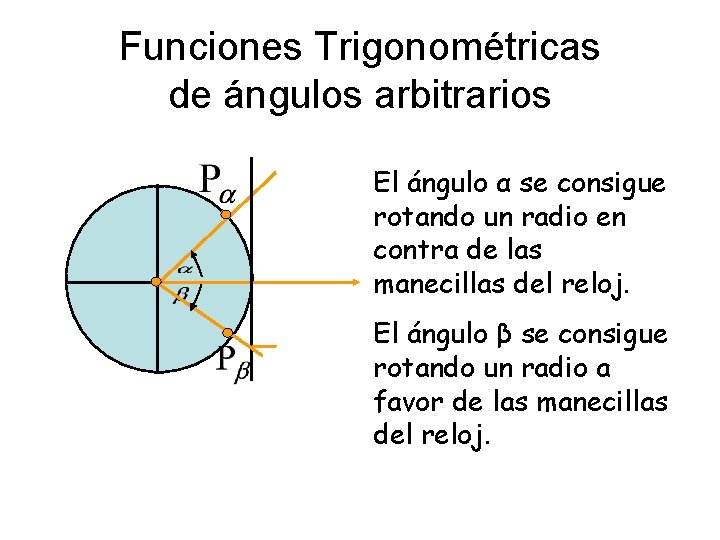
Funciones Trigonométricas de ángulos arbitrarios l El ángulo α se consigue rotando un radio en contra de las manecillas del reloj. El ángulo β se consigue rotando un radio a favor de las manecillas l del reloj.

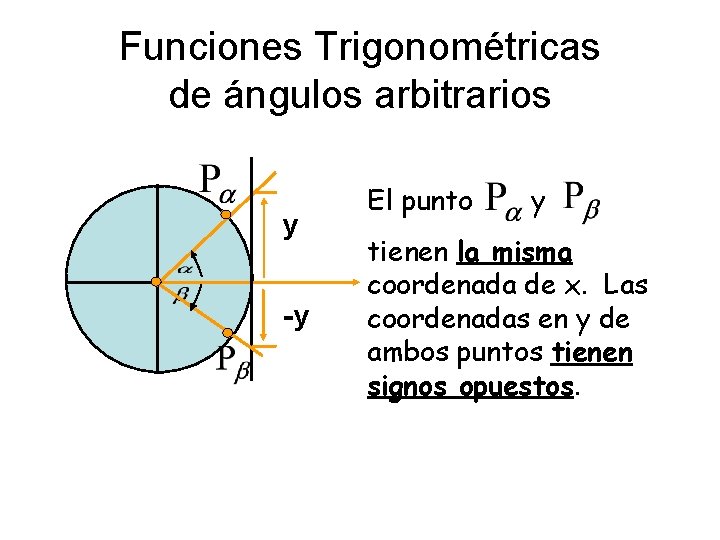
Funciones Trigonométricas de ángulos arbitrarios y -y El punto y tienen la misma coordenada de x. Las l coordenadas en y de ambos puntos tienen signos opuestos. l

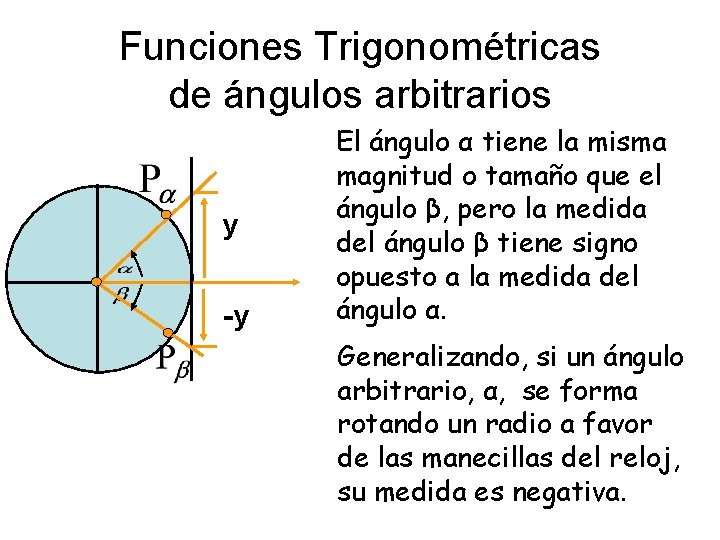
Funciones Trigonométricas de ángulos arbitrarios y -y l El ángulo α tiene la misma magnitud o tamaño que el ángulo β, pero la medida del ángulo β tiene signo opuesto a la medida del ángulo α. Generalizando, si un ángulo arbitrario, α, se formal rotando un radio a favor de las manecillas del reloj, su medida es negativa.

Funciones Trigonométricas de ángulos arbitrarios Para cada uno de los ángulos dibujados, dé la medida del ángulo faltante. l

Funciones Trigonométricas de ángulos arbitrarios Soluciones: l